Кинематический анализ механизма прижимной лапки вышивального полуавтомата

SEMIAUTOMATIC, MULTICOLOR, MACHINE EMBROIDERY, PRESSER FOOT, KINEMATIC ANALYSIS

In semiautomatic mechanism used mobile presser foot with elastic coupling between the links. This paper presents the results of the kinematic analysis of a mechanism to assess the impact of elastic coupling on the law of motion of the driven member.

EI staff « VSTU » and OPC « NP OKBM » designed semiautomatic multicolor embroidery on leather.

Compiled equations kinematics mobile foot with the infl uence of elastic coupling.

On the developed program of research carried out kinematic motion of the moving foot semiautomatic multicolor embroidery developed by the Department of machines and apparatus of light industry EI « VSTU » in conjunction with « NP OKBM » Vitebsk.

It was established that during the sewing detected light mobile take off foot traffi c from the source that does not create worsening conditions for the sewing process.

кинематики механизма подвижной прижимной лапки с использованием известных положений теории механизмов и теории колебаний. Цель работы – оценить влияние упругой связи на выполняемую прижимной лапкой технологическую функцию.

Схема механизма показана на рисунке 1. Ползун 2 получает движение от кривошипа АB через шатун ВС . Прижимная лапка 3 прижимается к ползуну пружиной 1. Представим механизм в виде системы, состоящей из двух звеньев – ползуна 2, совершающего движение по закону,

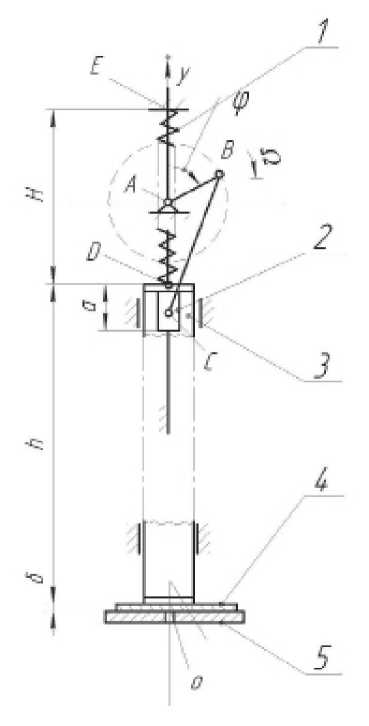
Рисунок 1 – Схема механизма

Без учёта динамики системы графики зависимостей у 1 и у ₂ от ф могут быть представлены соответственно в виде кривых I и II (рисунок 2 а ). На участках ab и da кривые I и II совпадают: прижимная лапка 3 и ползун 1 движутся совместно. На участке bd прижимная лапка неподвижна и прижимает сшиваемый материал 4 к игольной пластине 5, а ползун 3 движется вниз до точки с и возвращается в положение с координатой y₁ = h , где h – высота прижимной лапки 3 (рис. 1).

На рисунке 2 б представлены графики зависимостей скоростей V₁ и V₂ ползуна 2 и прижимной лапки 3 соответственно в виде кривых I и II.

Рассмотрим закон движения прижимной лапки 3 на участке da (рис. 2 a ). В начале участка ползун 2 движется со скоростью

„    . г2 япф-сохф , _....

,(2)

2           177

• >1 Лг -(г-81Пф)

где Q - угловая скорость кривошипа AB , ф = ф_d .

Уравнение (2) получено дифференцированием уравнения (1) по времени t. Лапка 3 в этот момент неподвижна. Таким образом, имеет место ударное взаимодействие ползуна 2 и прижимной лапки 3. Начиная с этого момента движение прижимной лапки 3 может быть представлено в виде уравнения определяемому размерами кривошипно–ползунного механизма АВС и прижимной лапки 3, совершающей движение под действием ползуна 2, пружины 1 и поверхности сшиваемого материала 4, играющей роль ограничителя. Угловую координату ф кривошипа АВ будем отсчитывать по часовой стрелке от оси Oy с началом 0, расположенным на поверхности игольной пластины 5.

Положение ползуна 2 будем определять координатой y ₁ точки, совпадающей с точкой D контакта пружины 1 с поверхностью прижимной лапки. Координата y ₁ определяется из формулы

,     (1)

где à – расстояние между центром шарнира С и D , r = АВ , L = BC .

Положение прижимной лапки 3 будем определять координатой y ₂ точки D контакта с пружиной 1.

; (3)

уг«ушу2<уг

Верхняя часть правой части уравнения (3) выражает свободные колебания прижимной лапки, где A – амплитуда сво бодных кол ебаний, м; c = 0,012 ю₀ , с^-1; ю₀ = V 1 / m • Xn , с^-1; m - масса прижимной лапки, 3 кг; Xn - осевая податливость пружины 1, м/Н; го₀ - круговая частота собстве нных кол ебаний прижимной лапки 3, с^-1; ю₀ = V ю₀² - с² ; а - начальная фаза свободных колебаний прижимной лапки 3, рад; h₀ – координата точки D пружины 1, находящейся в свободном состоянии, м; h₀ = y_e – H₀ ; H₀ – длина пружины 1 в свободном состоянии.

Величину V₀ определим из следующих соображений. При t = 0 имеет место ударное взаимодействие ползуна 3 и прижимной лапки 2. Согласно [3, с. 392], если движущееся тело (ползун

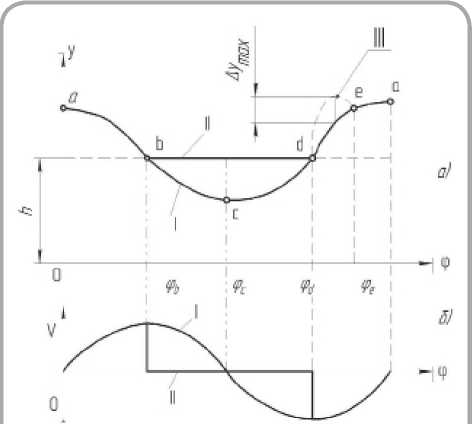
Рисунок 2 - Графики зависимости у1 и у2 от ф

• 3)    имеющее массу m₂ и скорость V₂ , ударяет в неподвижное тело (прижимную лапку 2) массы m, то конечная скорость после удара V₀ (общая для обоих тел) может быть определена из соот-

  ношения

  
  
  

  .

  
  

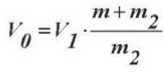
За массу m2 примем сумму приведенных к ползуну 2 масс: ползуна mÏ, шатуна mØ, криво- шипа тК и связанных с ним главного вала и звеньев привода: m2 = mn + т0 + тК. Так как m2 значительно больше m, то V0 ≈ V2 (формула 2).

Для определения постоянных А и а в уравнении (3) рассмотрим начальные условия: t = 0; y₂ = y₀ = y₁ – h₀ ; d · y₁ / d · t = V₀ . Подставив эти условия в (3), определим:

у₀ = А • sin a ;

V 0 = c • А • sin a + А • го • cos a .      (5)

Решая приведённую систему уравнений, определим:

.

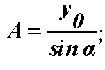
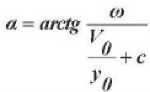
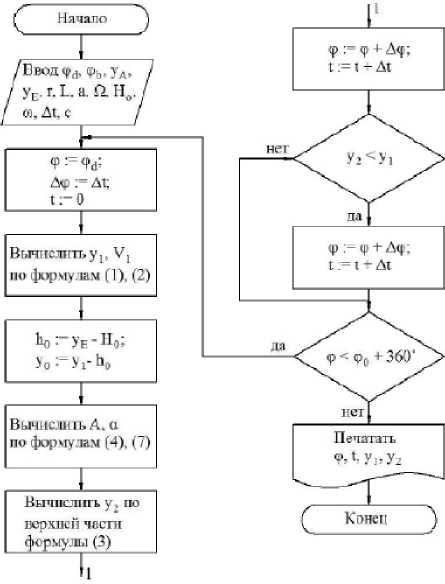
Нижняя часть уравнения (3) выражает совместное движение прижимной лапки 3 и ползуна 2. С учётом изложенного анализ движения прижимной лапки 3 может быть выполнен численным методом. Ниже предоставлена блок-схема алгоритма.

Нячапо

Конец нет

Вычислить у к, V] по фор му .лам (1), (2)

Вычислить А. а по формулам (4). (7)

Вычислить у, по верхней части формулы (3)

Др := Дт; t-0

<р ~9 +A

<р := Ф л- Д<р; t := 11- At

Ввод»* (рь,уд, уЕ. г. L. а. ПН,, о), At, с /

Ьо^:Уе ■ н₀;

У о •“ У г t*»

нет!

Печатать 9, t, у,,у2

Рисунок 3 – Блок-схема алгоритма

По приведённому алгоритму составлена программа расчёта положений ползуна 2 и прижимной лапки 3 на интервале [ф_d, ф_ь] значений ф по этой программе выполнены расчёты y₁ и y₂ для механизма прижимной лапки полуавтомата многоцветной вышивки на изделиях из кожи при следующих исходных данных: ф_d = 273°; ф_ь = 84°, y_A = 160 мм; y_E = 187 мм; r = 17,5 мм; L = 42 мм; a = 8 мм; Q = 100 рад/с; с = 0,012ф₀. Расчёты выполнены для пружин, спроектированных по методике, изложенной в [4] при различных требуемых усилиях прижатиях изделий из кожи.

На рисунке 2 а в виде пунктирной линии III показан график пути y₂ прижимной лапки 3, соответствующий [ф_d, ф_е ] углов ф, на котором имеет место нарушение контакта ползуна 2 и прижимной лапки 3. На интервале [ф_а, ф_ь]

Рисунок 4 – Образец распечатки результатов расчётов y₁и y₂

нарушение контакта ползуна 2 и прижимной лапки не наблюдается. Величину максимального расхождения графиков y₁ и y₂ на интервале [φ_d , φ_å] обозначим ∆y_max.

На рисунке 4 приведен образец распечатки результатов расчётов y₁ и y₂ , а на рисунке 4 – графики зависимостей y₁ = f(t) и y₂ = f(t), полученные на ЭВМ для пружины с диаметром проволоки d = 0,68 мм. Результаты расчётов для пружины с другими параметрами, спроектированных по методике, изложенной в [4], сведены в таблицу.

Из таблицы следует, что для всех пружин интервалы значений φ, в которых имеется нарушение контакта прижимной лапки 3 и ползуна 2, находятся в пределах φ = 278°…358°, а величина расхождения ∆y_max. ≤ 6,3 мм. Подобный закон движения прижимной лапки 3 не вызывает нарушения процесса шитья, так как на участке bd (рисунок 2 а) прижимная лапка контролирует сшиваемый материал.

ВЫВОДЫ

Предложена методика и алгоритм численного анализа кинематики механизма прижимной лапки.

С использованием этой методики проведен

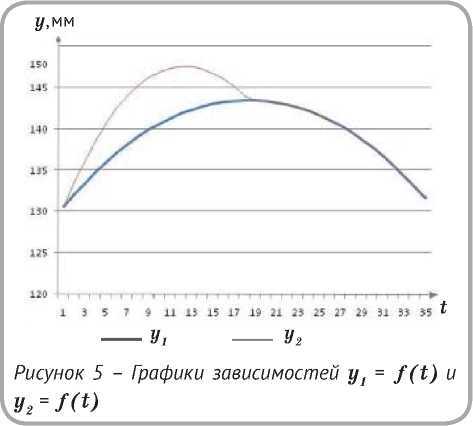
Таблица 1 – Результаты расчётов для пружины с другими параметрами № d, мм Ф4 • ° Фе • ° ^Утах • мм 1 0,32 278 353 6,010 2 0,41 278 358 6.190 3 0,47 278 358 6,231 4 0,52 278 358 6,244 5 0,56 278 358 6,251 6 0,59 278 358 6,254 7 0,63 278 358 6,256 8 0,65 278 358 6,257 9 0,68 278 358 6,306 10 0,71 278 358 6,259 11 0,73 278 358 6,260 12 0,75 278 358 6,260 13 0,77 278 358 6,260 14 0,79 278 358 6,261 15 0,81 278 358 6,261 16 0,83 278 358 6,261 17 0,85 278 358 6,261 18 0,87 278 358 6,050 19 0,88 278 358 6,262 анализ кинематики механизма прижимной лапки вышивального полуавтомата для различных пружин.

Установлено, что имеет место нарушение контакта ведомого звена механизма с ползуном кривошипно–ползунного механизма, которое не приводит к нарушению выполняемой технологической функции. Предложенная методика может быть использована при проектировании аналогичных механизмов переменной структуры с упругой связью.