Кинематика движения воздуха с твердыми частицами в каналах первого ротора роторно-вихревой мельницы тонкого помола

Движение газа вдоль поверхностей лопатки является непрерывным, т.е. циркуляция газа отсутствует. Согласно теореме Томсона [1], для замкнутого контура (поверхности лопатки) ^Г =0 , где Г – циркуляция и Г = const . В силу теоремы Стокса, такой поток газа будет потенциальным. Струи газа, движущиеся по выпуклой и вогнутой поверхностям лопатки, имеют разные относительные скорости. Разрыв скоростей движения газа на конце лопатки ( a - a ), образующей вихревые потоки разгонного типа.

Таким образом, при рассмотрении движения фракции материала при движении вместе с газом вдоль лопатки следует считать, что скорость частиц на выходе совпадает со скоростью газа.

Фактически скорости частиц и газа различны, что обусловлено лобовым сопротивлением газа движению частиц, определяемым по формуле [2]:

p= k„S лс =

|̅̅̅ ̅̅̅|(̅̅̅ ̅̅̅)

.

Уравнение для вычисления k_a при относительном движении сферических частиц получено в работе [3]. Тогда уравнение (1) принимает следующий вид:

лс = ^a ₈ Pc | ̅- ̅|( ̅- ̅),                             (2)

где d – диаметр частиц, мм; Pc – плотность среды; и – скорость относительного и переменного движений соответственно.

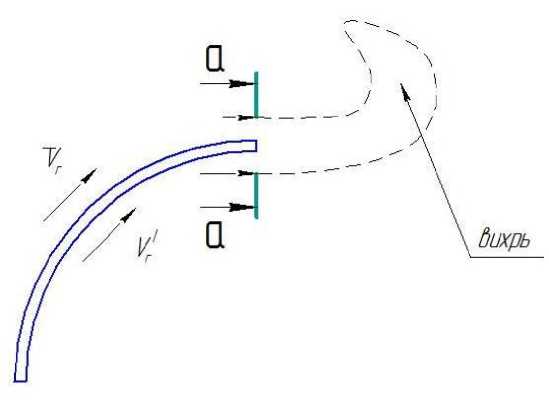
Рис. 1. Возникновение циркуляции вокруг профиля лопатки

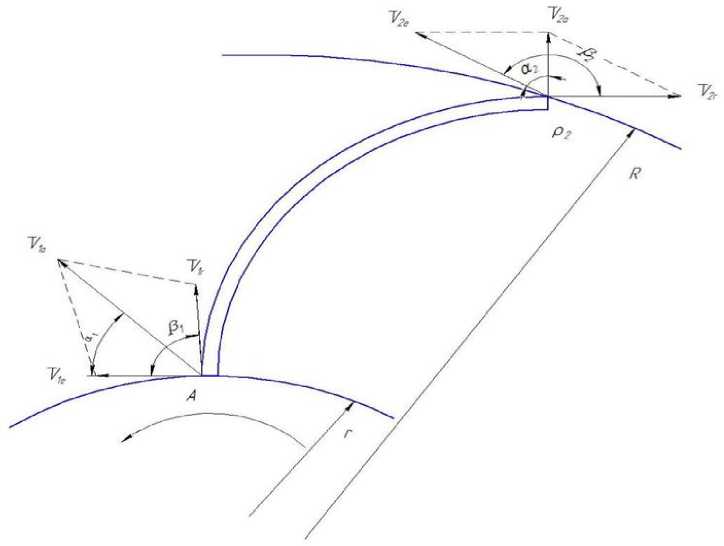
Рис. 2. Схема распределения скоростей

При вращении газ подхватывается лопаткой и движется по ней за счет центробежных сил от внутренней к наружной поверхности ротора. Частица измельчаемого материала, с газом попав на лопатку в точке А (рис. 2), совершает сложное движение, состоящее из относительного движе- ния частиц вдоль поверхности лопатки со скоростью ^1Г и переносного вращательного движения со скоростью ^le. Абсолютное движение со скоростью ^1(Z определяется как

̅ = ̅ ; + ̅ .

Направление относительной скорости ^lr не зависит от режима работы ротора, а определяется скоростью и направлением струи газа, тогда абсолютная скорость частицы геометрически равна

̅ la = ̅ le + ̅ lr .(4)

Модуль ^ld определяется по известной формуле теоретической механики:

^la =√Vie2 + ^lr2 +2 ^le × Vlr × Cos^ .(5)

Из формулы (5) следует, что чем больше угол $1 , тем условие входа газа в канал между лопатками лучше. На выходе из канала угол $2 наименьший и абсолютная скорость ^20, будет наибольшей.

Переносная скорость ^̅ ei зависит от расстояния до оси вращения ротора Ri и определяется по формуле:

Vs max =     =     ,                              (6)

где Ш_е переносная угловая скорость, C ¹.

Относительная скорость ^̅ зависит от скорости движения газа. При движении сферической частицы коэффициент сопротивления воздуха k_c функция скорости. Кроме того, на частицы действует сила трения, определяемая в первом приближении по закону Кулона. Для расчета скорости частиц используем дифференциальное уравнение вида:

m~dt =-(aVx +fтр), dVx     a . f     Pf

=-     +.

at    m \a /

Интегрируя данные уравнения, получаем:

( e~^-1).

Время движения частицы ( t ) определяется из выражения:

dt =   .

Значение ^xi изменяется от 0 до e . Таким образом, уравнение (8) примет вид:

dt =   .

Интегрируя уравнение (9), получим ^max _, т.е.

t = ^_ ^bmax TZ ^{, v}r max

где ^r max – максимальная скорость на конце лопатки.

При нарастании относительной скорости ^ri с учетом сил трения движение частицы из поступательного переходит в плоское. Двигаясь поступательно частица совершает вращательное движение. В связи с этим между частицей и поверхностью лопатки возникает тонкая прослойка газа и трение скольжения переходит в граничное трение. Сила трения в формуле (7) резко снижается и относительная скорость частиц возрастает.

Распределение скоростей по каналу рабочего колеса можно выразить через градиент дав- dP ления в канале . dx

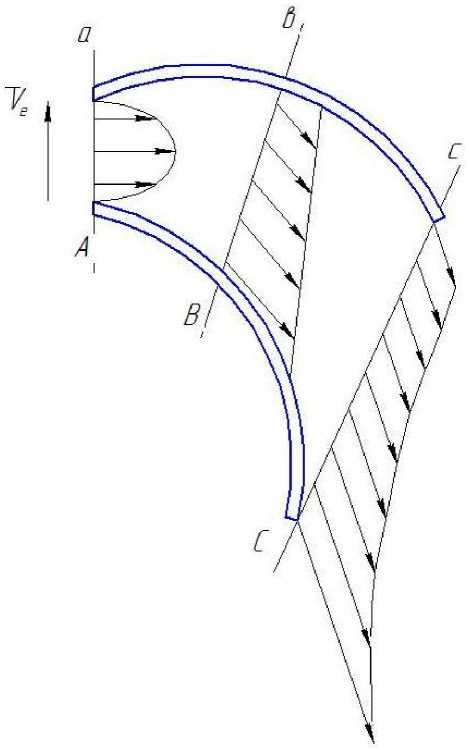
Рис. 3. Распределение скоростей по каналу как функция барометрического давления

dP

В сечении А - а градиент давления > 0 , т.е. происходит увеличение скорости газа. Для сечения В - в = 0 скорость движения газа постоянная. В сечении С - с градиент давления < 0 . При этом рост скорости газа замедляется. Это приводит к разряжению плотности газа. Так как скорость частиц газа на выпуклой поверхности больше, чем на вогнутой, то в сечении С - с образуется вихрь, закручивающий газ против часовой стрелки. Этому способствует переносная скорость ротора.

Если частица входит в канал в районе точки « ɑ » (рис. 3), то сила трения практически отсутствует и в формуле (7) её можно исключить. Следует также учесть, что под действием тангенциальной силы инерции частица приближается к выпуклой части лопатки. Контакт частицы с выпуклой поверхностью лопатки происходит в виде касательного удара в районе участка канала В - С (рис. 3). Угол У направления удара является острым и зависит от точки А касания частицы.

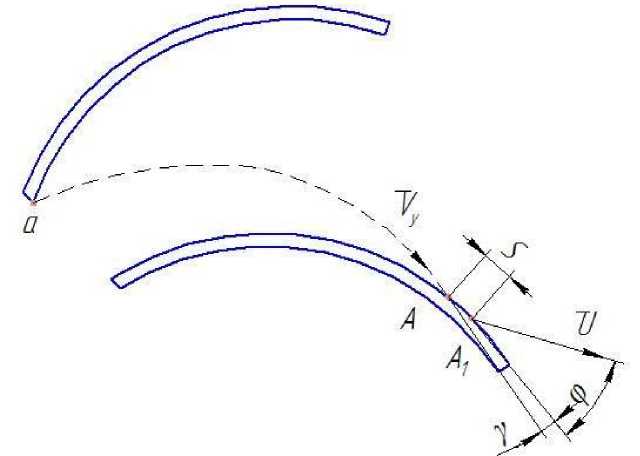
Рис. 4. Направление удара частицы и точка касания

После входа в контакт частица некоторое время скользит по рабочей поверхности лопатки. Расстояние s , пройденное частицей за время удара t_y , оказывается в точке А I . В результате упругого взаимодействия частица отскакивает со скоростью ^̅ под углом Ф к касательной в точке А ^:

U = √( Vy sin Y )²+( к ^∙ Vy соѕ Y )² , где к         ^;

Vy – скорость удара частицы, м/с.

При малом времени удара перемещение S соответствует предварительному смещению. Высокие контактные напряжения ^ак и тангенциальное смещение приводят к отделению микрочастиц с поверхности твердой частицы. Следует отметить, что чем больше угол падения Y , тем меньше износ сферической частицы. Следовательно, для наибольшего разрушения частиц кривизна лопатки выбрана таким образом, чтобы угол удара частицы на первом роторе был в пределах Y = (5 ÷ 10 ^° ) [4]. Кроме того, ротор 1 является разгонным и соответственно потери скорости частиц от ударов должны быть наименьшими [5].

Скорость отскока частицы U суммируется с абсолютной скоростью газа, в этом случае сферическая частица движется по криволинейной траектории в сторону выхода газа из межлопастного пространства.

Заключение . В процессе исследований установлен характер движения газа вдоль поверхностей лопатки первого ротора. Представлена формула для определения разности скоростей газа и частиц в его каналах, построена схема распределения скоростей на рабочих поверхностях ротора, определены точка входа частицы в межлопастное пространство и точка касания частицы поверхности лопатки (на выходе). Установлены критерии выбора кривизны лопатки.