Кинематика и алгоритмы управления 5D мехатронным устройством

Перспективность использования механизмов с параллельной кинематикой при построении технологического оборудования не вызывает сомнений, так как обладают рядом положительных качеств [1,2]. При проектировании технологического оборудования, построенного на основе таких механизмов, возникает потребность в решении задач кинематики и динамики.

Составление уравнений кинематики рассмотрено во многих публикациях, например [3, 4]. Эти уравнения могут использоваться при анализе рабочего пространства механизма с параллельной кинематикой [5], а также при решении траекторных задач применительно к технологическому оборудованию, построенному на основе подобных механизмов. При решении задач динамики возникает необходимость получить уравнения, позволяющие описывать поведение оборудования и его элементов, т. е. в построении динамической модели. Эти уравнения позволят осуществлять моделирование работы оборудования на качественно более высоком уровне, по сравнению с уравнениями кинематики, в том числе обеспечивать исследования динамических погрешностей при решении траекторных задач.

Рассмотрим механизм типа «гексапод» [3] и приводы, обеспечивающие движение элементов этого механизма. Гексапод включает в себя подвижную платформу, соединенную с основанием с помощью шести штанг, способных изменять свою длину (рис. 1).

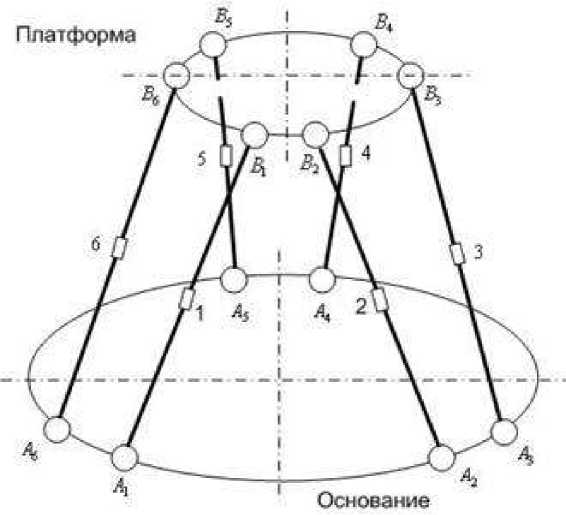
Рис.1

В таких устройствах, как гексапод и немецкий станок MetromP1000 используются подвижные приводы и поэтому длина шатунов в этих устройствах переменна. А у нашего устройства с параллельной кинематикой в местах стыка шатуна и толкателя установлен шаровый шарнир, и поэтому длина шатуна остается постоянной

На рисунке 2 приведена схема механизма с параллельной кинематикой. Подвижный рабочий стол предназначен для размещения на нем в центральной точке специального сопла «печатающей» головки с нагревателем, через который подается расплав неорганического вещества. Управляя положением сопла, с определенной ориентацией положения кромки сопла, на которой находится микро капля расплава, по трем декартовым координатам, с добавочными наклонами сопла по координатам Аи В (повороты вокруг оси Х и У), можно «напечатать» трехмерный каркас со сложной поверхностью и порами, имеющие сложную пространственную ориентацию. Число требуемых управляемых координат, для обеспечений пространственной ориентации рабочей точки, зависит, как от ориентации координат привода и их вида ( линейные или угловые перемещения), так и от числа степеней подвижности, которые обеспечиваются шарнирными опорами ( 2 или 3 степени).

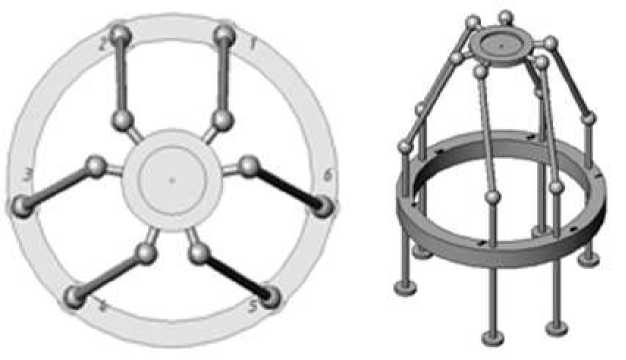
Рис.2. Кинематическая схема 5D-принтера..

(цифрами на неподвижном основании обозначены номера координат приводов – направление их движения ориентированы по оси Z )

В выбранной схеме все шаровые опоры имеют три степени свободы, все приводы обеспечивают линейное перемещение толкателей вдоль оси Z и расположены на образующей цилиндра с постоянным радиусом. Толкатели попарно сгруппированы, а пары,в угловом отношении, расположении под углом 120°. Аналогично попарно сгруппированы опоры на подвижном столе. Шатуны с шаровыми опорами имеют одинаковую длину. В отличие от других устройств, расположение приводов, как показано на рисунке 2, позволяет уменьшить расчеты, так как координата по оси Z «закреплена».

В данной работе рассматривается схема механизма с параллельной кинематикой, у которого все управляющие движения ориентированы вдоль оси Z, что позволяет исключить зависимость координат отдельногоi-ого привода от координаты Z рабочей точки подвижной платформы. Если рабочая точка подвижной платформы при движении по пространственновременной траектории требует изменения координатыZ, то все координаты исполнительных элементов приводов требуют изменения своего положения на такую же величину, что исключает в алгоритме управления необходимость этих расчетов.

Толкатели сгруппированы в пары, которые расположены симметрично относительно друг друга, а каждая пара расположена относительно других под углом 120°. Аналогично попарно сгруппированы опоры на подвижном столе, а сам подвижный стол повернут вокруг оси Z на угол 60°. Для обеспечения равномерной нагрузки и большей нагрузочной способности во всей зоне манипулирования, радиус расположения шаровых опор подвижной платформы выбран несколько меньше чем радиус расположения толкателей. При этом шатуны, передающие движение от толкателей подвижной платформе, имеют одинаковую длину. Заметим, что такое исполнение позволяет освободить весь внутренний объем механизма от каких-либо частей привода, поэтому пустое место может быть заполнено технологическими устройствами.

В большинстве работ, посвященных анализу механизмов с параллельной кинематикой, вне зависимости от расположения направлений движения исполнительных органов приводов и самой кинематики механизма, решается прямая задача: задано движение рабочей точки, и по аналитическим зависимостям требуется установить связь этих координат с координатами управляемых приводов в декартовой системе:

M(x,y,z,A,B,C)) = Р(р1,р2,р3,р4,р5,р6)

M ( r , ф , z , A, B ) = P ( pl, p2, p 3, p 4, p 5, p 6) (1)

Здесь векторы М и Р с координатами рабочей точки и, соответственно, каждого из приводов; координата (C - повороту вокруг оси z) рабочей точки платформы равна «0».

Действительно, любой механизм при создании проходит несколько стадий от идеи до реализации в опытной или серийной продукции. Это означает, что все параметры механизма, необходимые для расчета функциональной связи между пространственным вектором рабочей точки М платформы и вектором Р исполнительных механизмов приводов, известны. Поэтому эта часть алгоритма не требует его размещения в систему управления приводами. Результаты  расчета этого вычислительного алгоритма могут быть размещены в  массив или связанный список в следующем виде: ^^^^™                                                                    ^^^^™

M(x,y,z,A,B,C)) = Р(р1,р2,р3,р4,р5,р6)        (2)

В случае, когда конкретный механизм имеет некоторые отклонения от заданных номинальных геометрических размеров, являющихся параметрами сложного вычислительного алгоритма (1), в него могут быть внесены эти конкретные параметры и уточнен конечный результат вычислений (2) начальной задачи. Таким образом, на основе результатов вычисления может быть создан новый поисковый алгоритм определения текущих компонентов вектора приводов Р , на основе заданной пространственно - временной траектории.в пространстве вектора рабочей точки M . Объем памяти, занимаемый этой матрицей (связанным списком), определяется произведением чисел дискретных точек, необходимых для реализации с заданной точностью любые возможные пространственно – временные траектории в заданном объеме, манипулирования точки M .

На основании проведенных исследований механизма с параллельной кинематикой установлено, что вычислительную часть алгоритма не следует возлагать на систему управления приводами механизма, и тем самым существенно сократить требуемые вычислительные ресурсы системы. Это, по нашему мнению, существенно снижает стоимость таких устройств, и благодаря этому они становятся более доступны для своих пользователей.