Кинематика привода как функция угла поворота платформы манипулятора

Для исследования выбран оригинальный манипулятор, описанный в [1, c.65], [2, с.2], [3, с.2]. Кинематическая схема оригинальной части манипулятора представлена на рис. 1. Как было описано ранее, оригинальность данного пространственного манипулятора заключается в создании поступательного вертикального перемещения посредством двух встречных вращений наклонной платформы 1 и опорно-поворотного стола 2 [4, с.248].

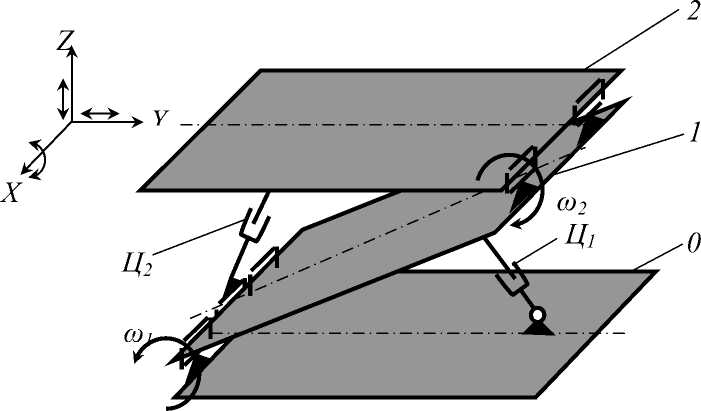
Рис. 1. Кинематическая схема оригинальной части манипулятора

0 - Основание; 1 – Наклонная платформа; 2 – Опорно-поворотное устройство; Ц1, Ц2 – Приводные устройства (гидроцилиндры).

Сведём движения манипулятора к моделированию соотношений в изменяемом «треугольнике», одна сторона которого изменяет свой размер и конструктивно исполнена, например, гидроцилиндром со штоком (рис. 2).

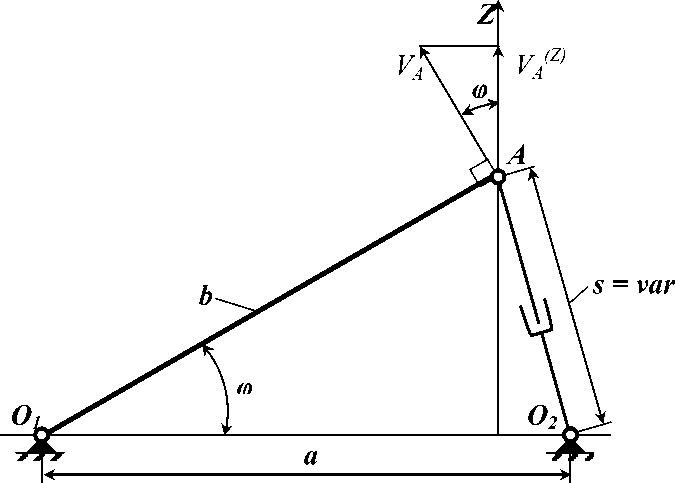
Рис. 2. Расчетная схема изменяемого треугольника механизма при s = var

s = О 2 А =var – изменяемая длина штока гидроцилиндра; О 1 О 2 = а = const – расстояние между опорами; О 1 А = b = const – длина наклонной платформы; φ = var – угол наклона наклонной платформы.

Рассмотрим движение манипулятора как функцию угла φ . Здесь можно рассмотреть 2 момента:

,у _ ds _

• 1)    изменение φ при ^{V =   = const} ,

ds

• 2)    изменение φ при V ^{=   = var} .

Из треугольника ∆О 1 АО 2 имеем:

s2 = a2 + b2

-

2a∙b∙cosφ ,

откуда

ф =

arccos

22 a + b

—

5 ² )

v    2 ab    7

,

при этом a = const, b = const.

Рассмотрим 2 случая:

1) Полагая, что s = V∙t ,

т.е. изменение суммарной длины s штока с

гидроцилиндром происходит

с постоянной

скоростью, т.е. V = const ,

выражение (1) запишется:

a

ф = arccos

² + b b

—

( a b V²

v    2 ab    7

= arccos-- 1--

( 2 b 2 a

—

• t

2 ab

Выбирая конструктивно параметры так, что a = b выражение

_V 2    ₂

преобразуется: ^ф = ^arccos(1   —2- • t ) или

V 2    2 ф (t ) = arccos(1-- у • t ) 2 a 2

(3)

• 2)    Изменение суммарной длины s штока с гидроцилиндром происходит с переменной скоростью, т.е. V = var , выражение (2) запишется:

  .          (    V2    ,^ ф ( V , t ) = arccos 1 •• t I    2 az     J

  (4)

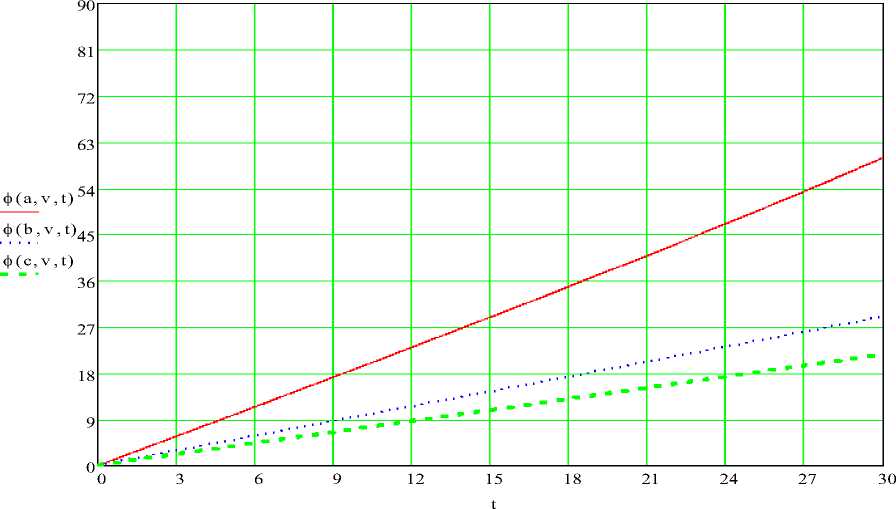
Используя пакет программы MathCAD 14, приводим зависимости выражений (3), (4) которые представлены на рис.3( а , б ) и рис. 4( а , б ).

а)

v := 0.0]   t := 0 , 0 + 0.01 .. 30     a := 0.2 b : = 0.0 c : = GJ

б)

v := 0.02   t := 0 , 0 + 0.01 .. 30

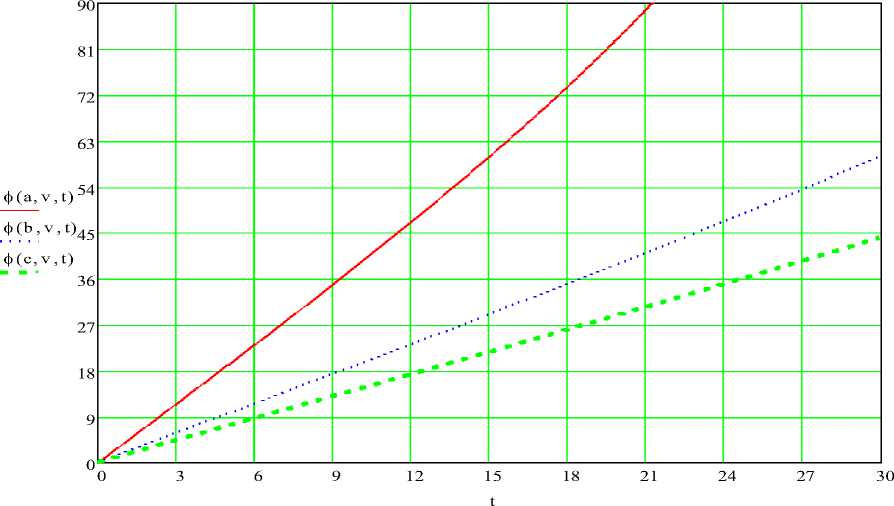
Рис. 3. Зависимость угла поворота наклонной платформы ф(а, V, t) от времени t = var при разных скоростях штока гидроцилиндра

0 0

в)

t := 10    v := 0 , 0 + 0.01 .. 0.

^ф (b , v ,045 ф (c , v , t)

ф (a , v , t)54

				♦
			*
		♦
		♦
	/ ♦ ? +
/ ?>	t
/ '^

0.02

0.04

0.06

0.08

0.1

0.12

0.14

0.16

0.18

v

0.2

г)

t := 10     v := 0 , 0 + 0.01 .. 0.:

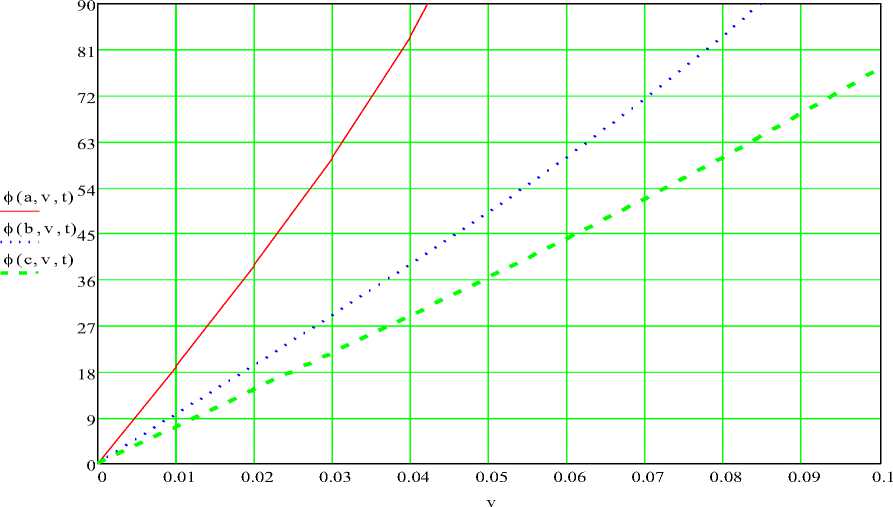
Рис. 4. Зависимость угла поворота наклонной платформы ф(а, V, t) от скорости движения штока V = var

Выводы:

1) с увеличением скорости движения штока гидроцилиндра V, поворот платформы осуществляется быстрее;

2) зависимость

ф ( V, t ) = arccos 1

к

V ² 2 a ²

• t^т

при V = 0,01

- 0,02 м/сек и

t≤ 12 сек , практически линейна;

• 3)    в рабочем диапазоне изменение угла α = 0° - 45° и угловая

скорость движения наклонной платформы 1 (или опорно-поворотного устройства 2) изменяются незначительно, что благоприятно для работы манипулятора.