Кинетические модели распространения и тестирования эпидемических заболеваний в изолированном контингенте
Автор: Чигарев А.В., Чигарев В.А., Адзерихо И.Э.
Журнал: Российский журнал биомеханики @journal-biomech
Статья в выпуске: 2 (92) т.25, 2021 года.
Бесплатный доступ
Рассмотрено обобщение классической SIR -модели распространения инфекций. Обобщение моделей проведено по двум направлениям: 1) с учетом тестирования (мониторинг), которое проводится на практике во всех странах, за счет расширения SIR -модели путем включения модели наблюдения; 2) с учетом отсутствия достоверной информации о состоянии контингента людей (распространение заболеваний моделируется случайными процессами (рандомизация), статистика которых определяется алгоритмами оценивания Калмана-Бьюси). Полученная модель математически является более корректной, устойчивой, что позволяет получать более достоверные оценки процессов инфицирования. Модель оценивания, полученная за счет расширения, описывается уравнениями, соответствующими методу регуляризации при решении некорректных задач. Полученная система уравнений одновременно с оценкой состояния позволяет находить погрешность оценивания. Для оценивания процесса инфицирования, когда количество выздоровевших, умерших в целом мало по сравнению с числом подверженных инфицированию и инфицированных, используется обобщающая модель Лотки-Вольтерра естественного течения эпидемического процесса. На основе полученной модели рассмотрено решение эталонных задач. Получено решение для оптимальной оценки и её погрешности на начальной стадии инфицирования, когда можно считать, что наблюдаемое число инфицированных линейно растёт в зависимости от времени, а погрешность оценивания в начальный момент времени велика относительно числа действительно инфицированных. Получение достоверных наблюдений является основой для принятия эффективных решений по борьбе с эпидемией. Разработанная модель отражает существующую на практике неопределенность в оценивании уровня эпидемического состояния контингента. Рассмотрена эталонная задача, когда оценка числа инфицированных является функцией, которая изменяется в зависимости от времени, хотя в действительности число инфицированных во времени остается постоянным (стационарное состояние). Таким образом, в рамках модели описывается эффект псевдоэпидемии, который может существовать в контингенте с постоянным суммарным числом всех групп.
Кинетические уравнения, модели, инфицирование, наблюдения, рандомизация, sir-модель
Короткий адрес: https://sciup.org/146282198
IDR: 146282198 | УДК: 617.3 | DOI: 10.15593/RZhBiomeh/2021.2.02
Текст научной статьи Кинетические модели распространения и тестирования эпидемических заболеваний в изолированном контингенте
Современные кинетические модели эпидемий, в том числе COVID -19, позволяют описать различные аспекты развития эпидемии в основном за счет расширения и детализации структуры исследуемого контингента людей, среди которых происходит распространение инфекции.
Создание удачной эвристико-математической модели это, как правило, задача минимакса. С одной стороны, модель должна быть максимально адекватной реальности, что обычно достигается за счет расширения размерности пространства состояний системы (количества групп контингента: здоровые, больные, иммунизированные, выздоровевшие и т.д.). Математически это выражается в увеличении количества кинетических уравнений, что создает проблему «проклятие размерности». С другой стороны, огрубление модели за счет уменьшения (минимизации) числа значимых переменных состояния не может проводиться произвольно, а должно опираться на законы теории грубости, такие как топологическая грубость [1], структурная устойчивость [11, 13].
Существующие модели эпидемий описывают естественный ход событий, что даже на уровне простейших моделей позволяет учесть некоторые явления, присущие естественному развитию эпидемий [8, 9]. Практика COVID -19 показала, что в современных условиях происходят различного рода вмешательства в процесс, причем воздействия эти носят не только медицинский характер, но и социальный, административно-политический, экономический. Таким образом, создание адекватной модели распространения инфекции должно предполагать привлечение моделей социодинамики, экономики, управления, наблюдения, идентификации.
Это можно сопоставить с проблемой создания погодно-климатических моделей, в которых учитывается «эффект бабочки». Однако, как показала практика, точность прогнозов на основании таких моделей не соответствует затраченным усилиям. Поэтому согласно теории грубости в качестве базовой модели выбирают какую-либо модель, отражающую основные свойства реальной системы и имеющую по крайней мере качественное сходство с реальной. На этой стадии моделирование носит эвристический характер [4, 10], базируясь на квалификации специалистов, на данных наблюдений.
Моделирование системы с учетом антропогенных факторов включает в себя модели наблюдения, идентификации и управления. Практика борьбы с COVID -19 показала важность учета тестирования при создании математической модели, поэтому рассмотрим прежде всего, как влияет учет наблюдений на качество создаваемой модели. Из опыта борьбы с распространением инфекции короновируса следует, что точное определение в контингенте различных групп людей, т.е. квалификация их состояния, содержит во многих случаях элемент неопределенности и, таким образом, задачи тестирования, идентификации, принятия решений, управления решаются в условиях неполной информации, что требует реализации известных детерминированных моделей [5, 6]. Введение модели наблюдений требует учитывать тот факт, что во всех реальных системах (системах с неполной информацией) любые наблюдения, измерения состояния содержат ошибки, которые имеют случайный характер. Это должно быть отражено в модели.
Отметим модель [5, 6], которая описывает кинетику инфицирования и в принципе содержит SIR ( susceptible infections recovered )-модель эпидемии.
Расширение в SIR-моделях за счет тестирования
Математическая SIR -модель инфекционного процесса для фиксированного контингента людей представляет собой систему дифференции уравнений, описывающих кинетику взаимодействующих агентов типа последовательных химических реакций.
Пусть контингент состоит из здоровых людей, в который в момент времени t = t0 попадает один инфицированный человек. В дальнейшем количество инфицированных равно I или I ( t ) < N . В момент времени t0 ^ t
N = S ( t ) + 1 ( t ) + R ( t ),
где S ( t ) - число людей в контингенте, которые могут быть инфицированы, т.е. перейти в группу I ( t ); R ( t ) - число людей, перешедших из группы I ( t ) в группу R ( t ) -выздоровевших.
С точки зрения кинетики целесообразно перейти от функции S ( t ), I ( t ), R ( t ) к i ( t) = IN - 1, 5 ( t ) = SN - 1 , r ( t ) = RN - 1, для которых имеют место уравнения [10]
*«■ - - di
— = в 51-у i; dt dr
— = yi. dt
Система уравнений (2) нелинейная. Введя вектор состояния x ( t ) = ( 5 , i , r ) T = ( xv , x 2, x 3) T ,
запишем уравнения (2) в виде dx
— = F ( t , x ), x ( t о ) = x (0) = x 0. dt
Учтем, что в системе (4) ведется мониторинг, т.е. берутся выборки (тесты). В общем случае не все компоненты вектора x (t) могут быть измерены непосредственно, некоторые только опосредованно. Обозначим вектор измеряемых величин y(t) , который в общем случае связан с x(t) зависимостью y (t) = Ф [ x, t ], y = (y,,..., Ут), m < n. (5)
Рассмотрим для наглядности и общности уравнения (4) в линеаризированном виде. Линеаризацию проведем в окрестности стационарного x(t) состояния, которое находится из уравнений dx
— = 0 = F ( x 0 +в x ,, t ).
Из (6) получаем последовательно dx — —
-
-т° = о = F ( x о);
dt dx
----= Ax, .
dt 1
Модель наблюдения имеет вид y о = Ф[ x о ]; y 1 = Cx i,
где А , С – матрицы.
Согласно теории оценивания состояний систем с числом переменных состояния, превосходящих число величин, доступных непосредственному измерению (тестированию), кинетика распространения инфекции может быть описана системой уравнений Калмана–Бьюси, имеющих вид [12]
— = (A — GC)Z + Gy dt где z - оценка переменной состояния xi; А - матрица системы; G - матрица (в частности, вектор, скаляр) такая, что матрица А – GC является устойчивой [12].
Погрешность оценки z для x i обозначим как е = z — xi. Имеет место уравнение для погрешности de-
— = (A — GC)e.(11)
Для рассматриваемой SIR-модели (2) система имеет вид ds Y .
-
1 = -—s
dtP у dir = (Ps о — Y) ii+ 3 iо si;
dt dr 1•
— = Y ii, s о + Г = L i о = —• dtN
Так как в рассматриваемом примере I (о) = i, | z (о) = — | для о < t , то для
V N J погрешности оценки e и оценки z в уравнениях (9), (10) положим А = 0, тогда получим e = e о exp(—C) t •
Соответственно, для z получим в векторно-матричном виде выражение z = zо exp[(GC)t]j Gy(t)exp(—GC)tdt, z0 = (о, i, о). (14)
Формулы (13) и (14) показывают, что если в начальный момент t = 0 тестирование дало ошибку e ^ (о, о, о), то оценка дальнейших состояний при t > 0 также будет содержать ошибку z ^ (о, о, о)T, e ^ (о, о, о), которая со временем убывает. На протяжении некоторого времени 0 < t может иметь место псевдоэпидемический эффект, обусловленный ошибкой измерений, а не биологическими, медицинскими причинами. Этот эффект далее рассмотрим для статистической модели.
Вероятностное обобщение SIR-модели (рандомизация)
Преобразуем уравнение (1) детерминированной SIR -модели [7] в стохастические дифференциальные уравнения, добавив в правую часть вектор ошибок, описываемых случайными функциями v к [12] типа белого шума:
dsN
-
— = -р si + -1 v , ( t );
df2
diN
-
— = P si -Y i +v 2 ( t );
dt2
drN
= Y i + -A v 3 ( t );
dt2
(v , ( t ) ) = 0, (v , .( t 1 ) v j ( t 2)} = N j -6 ( txt 2).
Система (15) является частным случаем системы кинетических уравнений, обобщающих систему (2).
dx = F [ t ; x ( t ) ] + G ( t ) Y ( t ).
Модель наблюдения (4) обобщается на стохастические системы
z ( t ) = Ф ^ t ; x(t ) J + n ( t ), t 0< t ;
( n (t )} = 0 nii(tj nj (t 2^ = nj 5( ti - t 2), где n – вектор ошибок измерения (тестирования).
Обозначим апостериорную плотность вероятности вектора состояния x ( t ) через
P ( x ; 11 z t о t ), (18)
где z t о t - вектор наблюдений (тестирования) на интервале [ t о , t ].
Как известно, математическая модель (16), (17) описывает функцию x ( t ) марковского типа, для которой P ( x ; 11 z t о t ) удовлетворяет уравнениям типа ФПК (Фоккера–Планка–Колмогорова) [6].
Обозначим x (t) вектор оценки состояния, который минимизирует средневозрастную квадратичную ошибку оценивания:
E min = (( x ( t ) x ( t ) T \ (19)
Обозначим ковариационную матрицу ~( t ) процесса x ( t ):
V ( t ) = (( x ( t ) - x ( t )( x ( t ) - x ) T У (20)
Очевидно, матрица v(t) характеризует среднеквадратическую погрешность оценивания процесса x(t) с помощью оценки x (t).
Согласно теории оценивания [6], для x ( t ) и v(t ) на основе уравнений для апостериорных плотностей вероятностей ФПК получается уравнение вида
,x
-| = F [ t , x ( t ) ] + V ( t ) D [ h ( t ), x ( t ) ] n4 { z ( t ) - h [ t ; x ( t ) ]} , x ( t , ) = x , ,
dh [ t ;x ( t ) ] dx i
x где D[h(t); x (t)] - матрица Якоби mxm с элементами dV = DT [ f (t; x (t)] V (t) + V (t) D [ f (t; x (t)] + G (t) XGT (t) + V (t) D [ h (t) x (t) ] +
+ N -1 { z ( t ) - h ( t ) x ( t )} V ( t ), V ( 1 0 ) = V ,. (22)
Замкнутая связанная система уравнений (21), (22) в принципе позволяет получать точные или численные решения задач оценивания для стохастических моделей эпидемий с тестированиями. В общем случае системы нелинейные, что значительно усложняет получение решений, особенно в аналитическом виде, поэтому имеет значение получение аналитических решений в конкретных интересных случаях.
Как известно, сокращение числа степеней свободы в системе может вести к ее самоорганизации [12]. Например, в модели Лотки–Вольтерры [3] скорость инфицирования сначала растет, а затем по достижении некоторого значения начинает убывать, что имеет место в реальности.
Поэтому положим, что скорость выздоровления dr/dt значительно меньше, чем скорость инфицирования, тогда можно в (2) положить dr/dt ® 0, откуда следует y = 0 и SIR-модель преобразуется в SI-модель [6], уравнения которой для стохастической модели с измерениями запишем в виде ds
= -р si + G i V i ( t ); (23)
dt di
-
= p si + G 2 v 2( t );
dt
(V i ( t ) ) = 0, (Vi ( t i ) v i ( t 2 )) = N u 5 ( t i - t 2 ); (24)
z ( t ) = i ( t ) + V ( t ) ;
-
V ( t ) = 0, V ( t ,) V ( t 2) = W § ( t j - t 2) .
Преобразуем уравнение (23) с учетом N + N = N к виду d1 = pi |1 + — - i | + G2v2 (t). (25)
dt ( N J 22
Уравнения (24), (25) являются математической основой для получения оценок состояния процесса инфицирования и его прогнозирования, обобщающих модель Лотки–Вольтерры.
Эталонные задачи оценивания для начала процесса инфицирования
Рассмотрим случай, когда в начальный момент времени в некоторый изолированный контингент N людей попадает один инфицированный человек, причем в системе постоянно ведутся измерения (выборки), которые в реальности всегда содержат неопределенность, т.е. случайную ошибку. В частности, положим, дисперсия ошибки V(t) при t = 0 равна 10.
Уравнения (21), (23) в данном случае имеют вид di
-- = Р i dt
1 + — — i N
+ V (t) [ z (t ) -i( t ) ] ;
dV = —[ V ( t ) ]2, V (0) = 10. (27)
Решение системы (26), (27) начинаем в обратном порядке. Решение V ( t )
уравнения (27) имеет вид
V ( t ) =
10 t + 1
Уравнение (26) типа Риккати преобразуем к линейному с помощью замены [2]:
i ( t ) =----- .
U ( t )
Тогда уравнение для u(t) имеет вид du
— + p a (t ) u = f (t ),
dt где a (t) = p 1 + —
—
V"
f(t ) = p— V(t ) z(t ), u 2(0) « u4t ) « 1.
Решение (30) имеет вид [3]
u ( t ) = Й1) U f ( t >Ц< t ) dt + C ] ’ ^ ( t ) = e ^ a ( ‘ ) d
•
Уточним модель наблюдения, приняв для простоты, что вначале наблюдения дают линейный рост во времени числа инфицированных. Это допустимо в начале процесса инфицирования.
z (t ) = t + 1/10. (32)
Тогда для оценки плотности (числа) инфицированных получим оценку
_ e p (1 + 1/ N ) t rn — 1
i =-------- ----
10 + 1
e b Ei ( ab + at ) — Ei ( ab ) + 1
ax e , Ei ( x ) = —dx ,
x
где Ei ( x ) - интегральная показательная функция [12].
Рассмотрим модель псевдоэпидемии. Положим, что в начальный момент в изолированный контингент попадает один инфицированный человек, но система остается в стационарном состоянии:
di ds dr dt dt dt
Положим, что в системе проводятся замеры, которые могут содержать случайные ошибки, дисперсия которых V ( t ) при t = 0 равна 10 (большая).
Математическая модель инфицирования в этом случае описывается уравнениями
di = о, i (0) = 1, dt z (t) = i (t) + v (t), (v(t)) = 0 vV(t1)v(t2>) = 8(t1 - t2)-
~
~
Уравнения для оценки i ( t ) и погрешности оценивания V ( t ) в рассматриваемом случае получаем из (26), (27).
Уравнение для V ( t ) в этом случае совпадает с (27), а его решение имеет вид (28).
Уравнение (26) для оценки i ( t ) имеет в этом случае вид
di- = -10-Г z ( t ) - i ( t ) 1 , i (0) = 1. dt 10 t + 1 L J
При линейной зависимости наблюдений z(t ) от t решение (36) имеет вид
5t2 + 1 г ( t ) =
10 t + 1
.
Таким образом, ошибка в начальном измерении V (0) * 0 ведет к возможности появления ошибок при тестированиях при 0 < t , причем ошибка i ( t ) в определении состояния убывает до t * 0,35, а затем растет как парабола. Это псевдоэпидемический рост инфицирования, который описывает влияние ошибочных результатов тестирования (рис. 1).
Скорость инфицирования характеризуется величиной d^L = -5t2 + 2 2 -103.
dt2 (10 t + 1)3
Условие экстремума скорости инфицирования дает 2 = 5 t 2, t , = 21 (рис. 2).
При t > ^ 2/5 производная > 0, при t < V2/5 < 0, следовательно, оценка скорости инфицирования сначала растет, потом убывает, что характерно для естественного течения эпидемии.
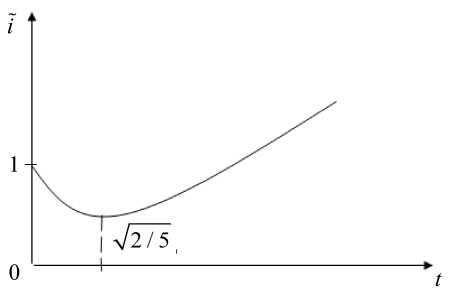
Рис. 1. Зависимость оценки плотности инфицирования i от времени
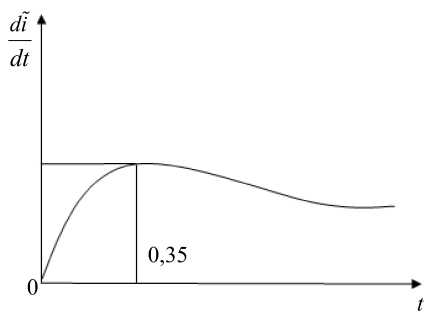
Рис. 2. Зависимость скорости инфицирования от времени
В фазовой плоскости ( i, i ) имеем уравнение фазовых траекторий
i i + 101 +1
= 1,
которые изображены на рис. 3.
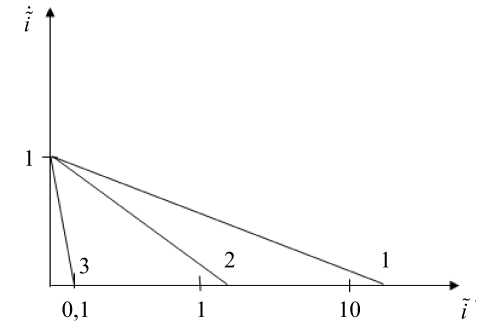
Рис. 3. Фазовые траектории i ( i ) при 1 - 1 = 0, 2 - 1 = 1, 3 - 1 = 10
Заключение
-
1. Модель SIR естественного распространения инфекции в изолированном контингенте обобщена с учетом результатов наблюдений (выборок).
-
2. Учет факта, что распространение инфекции происходит в условиях неполной информации, реализуется за счет преобразования детерминированной SIR -модели в стохастическую.
-
3. Для оценок и ошибки оценивания используются уравнения теории оценивания Калмана–Бьюси, на основе которой рассмотрено получение аналитических решений и их погрешности в эталонных задачах.
-
4. Рассмотрена модель псевдоэпидемии, которая может быть получена при ошибках измерений в начале эпидемии.
Список литературы Кинетические модели распространения и тестирования эпидемических заболеваний в изолированном контингенте
- Андронов А.А., Понтрягин Л.С. Грубые системы // ДАН СССР. - 1937. - Т. 14, № 5. - С. 247-250.
- Камке Э. Справочник по обыкновенным дифференциальным уравнениям. - М.: Наука, 1971. -576 с.
- Канторович Л.В., Горстко А.Б. Оптимальные решения в экономике. - М.: Наука, 1972.
- Оморов Р.О. Метод топологической грубости динамических систем; приложения к синергетическим системам // Научно-технический вестник по информационным технологиям механики и оптики. -2020. - Т. 20, № 2. - С. 257-260.
- Русаков С.В., Чирков М.В. Идентификация параметров и управление в математических моделях иммунного ответа // Российский журнал биомеханики. - 2014. - Т. 18, № 2. - С. 259-269.
- Чирков М.В. Идентификация параметров математических моделей инфекционных заболеваний на основе метода Монте-Карло // Математическое моделирование в области клеточной биологии, биохимии и биофизики: материалы научно-практической internet-конференции, 25-26 ноября 2014. -Ульяновск, 2014. - С. 93-96.
- Bacaër N. Un modèle mathématique des débuts de l'épidémie de coronavirus en France // Mathematical Modelling of Natural Phenomena. - 2020. - Vol. 15. - P. 29. DOI: 10.1051/mmnp/2020015
- Dong E., Du H., Garden Z. An interactive web-based daviboasol to track covid-19 in real time // The Lancef Infections Dieses. - 2020. - Vol. 20, no. 5. - P. 533-534. DOI: 10.1016/S1473-3099(20)30120-1
- He S., Peng Y., Sun K. SEIR modeling of COVID-19 and its dynamics // Nonlinear Dynamics. - 2020. -Vol. 101, no. 3. - P. 1667-1680. DOI: 10.1007/s//071-020-05743-Y
- Kenny V., Nathal M., Saldana S. Heuristic algorithms, avaliable at: https://optimization.mccormick. northwestern.edu/index.php/Heuristic_algorithms (5 March 2021).
- Picxoto M.M. On structural stability // Ann. Math. - 1959. - Vol. 69, no. 1. - P. 199-222.
- Sade A.P., Melse J.L. Estimation theory with application in communication and control. - New-York: McGraw-Hill Book Co., 1972. - 529 p.
- Thompson J.M.T. Instabilites and cafastrohes in science and engineering. - Chichester: Wiley, 1982. -226 p.


