Кинетические модели роста дрожжевой биомассы

Введение. Большинство используемых в промышленности микроорганизмов являются гетеротрофами, для жизнедеятельности которых необходимы органические источники углерода. В процессе жизнедеятельности микроорганизмы осуществляют разнообразные функции, которые обусловлены высокой степенью организации клеток и их сложной структурой. В ходе жизнедеятельности микроорганизмов клетки непрерывно претерпевают как количественные, так и качественные изменения: рост, изменение химического состава, морфологии, размножение, спорообразование и, наконец, отмирание.

Дрожжи, как правило, размножаются почкованием. На клетке образуется почка, которая растет до размеров материнской клетки, а достигнув ее размеров отделяется.

В настоящем исслеодвании мы задались целью выяснить кинетическую модель роста дрожжевой биомассы, необходимой при производстве теста.

Методика. В данной работе по определенной рецептуре (ГОСТ 27844-88, ингредиенты уменьшены в три раза) смешивали все компоненты в определенной последовательности, а именно, для опары: мука пшен., в/с - 165г, вода - 85 г, дрожжи сухие - 3 г; для теста: опара + мука -135 г, вода - 75 г, сахар-песок -12 г, соль - 4,5 г, масло - Юг.

После этого вели наблюдения нарастания дрожжевой биомассы во времени с использованием аналитических весов ВЛТЭ-150 с точностью взвешивания в 0,003 мг. Далее строили кинетическую кривую нарастания тестовой массы.

Результаты и обсуждение. Полученная в ходе наблюдений кинетическая кривая представлена на рисунке. Видно, что кинетическая кривая нарастания биомассы теста во времени имеет сложный характер (Бейли, Оллис, 1989); в ней выделяют несколько фаз.

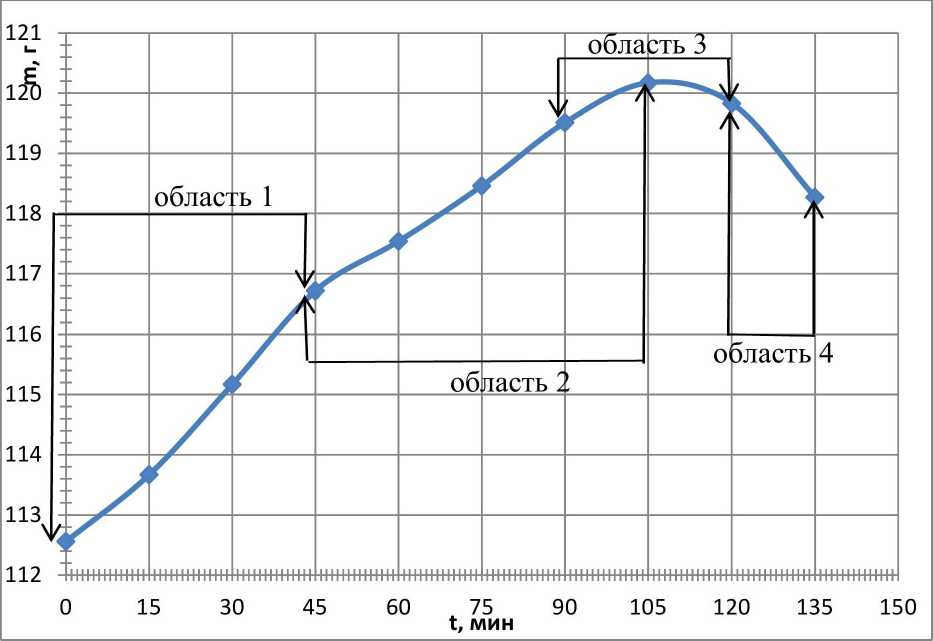
Рисунок. Кинетическая кривая нарастания тестовой массы

I фаза (лаг-фаза) - индукционный период, в течение которого не происходит сколь-нибудь заметного возрастания биомассы (увеличения числа клеток) или образования каких-либо продуктов. В этот период перестраивается метаболизм исследуемой системы, синтезируются ферменты, специфичные к использованию новых субстратов. Активируется биосинтез белка и т.д. Обычно эта фаза минимальна по протяженности. Этой фазы мы не наблюдали, возможно, в связи с тем, что рецептура по составу и количественному соотношению компонентов настолько оптимальна, что перестройка метаболизма не требуется, а сразу наблюдается экспоненциальный рост.

II фаза - индукционный период сменяется фазой экспоненциального роста, в течение которого быстро накапливаются биомасса и продукты разных реакций. На нашей кинетической кривой эта фаза (область 1) выявляется с 15 до 45 мин и сопровождается возрастанием с 112,56 г до 116,72 г тестовой массы на 3,4 % массы теста от исходного количества. Эта фаза достаточно строго описывается экспоненциальной кривой. Однако следует иметь в виду, что в замкнутой системе экспоненциальная фаза роста нс может развиваться неограниченно. Как правило, она переходит в следующую фазу.

• III    фаза - фаза линейного роста, которая характеризуется равномерным во времени линейным нарастанием биомассы. На нашей кинетической кривой эта фаза (область 2) занимает промежуток с 45 по 90 мин наблюдения. В этой фазе уже не наблюдается линеаризация -44 -

• кинетической кривой нарастания биомассы в полулогарифмических

координатах; имеет место отклонение точек в сторону меньших значений биомассы или продуктов, что служит экспериментальным критерием перехода тестовой массы в линейную фазу роста. Фаза линейного роста может смениться весьма непродолжительным периодом, в течение которого скорость нарастания биомассы снижается до нуля (область 3). Следом за ней наступает последняя, IV фаза.

• IV    фаза (область 4) - фаза замедления нарастания биомассы. Эта фаза наблюдалась нами с 120-й мин до 135 мин. Снижение массы теста в этот период происходило на 1,7 %.

В результате проведенных экспериментальных исследований зависимости скорости нарастания массы дрожжевого теста были обнаружены две особенности:

Скорость изменения числа микроорганизмов в режиме его роста (в экспоненциальной фазе) линейно связана с концентрацией клеток в системе:

dN ..

— = pN, dt ’ где N - число клеток (масса), д - коэффициент пропорциональности,

1 dN\

--; имеет

N dt /

получивший название удельной скорости роста

^ =

размерность обратного времени. Расчет ц позволил получить значение, равное 7,5-10"⁴ мин"¹ Предполагается, что р не зависит от времени в исследуемом интервале. Собственно, это уравнение в интегральной форме и представляет собой уравнение экспоненциального роста. Его интегрирование при начальном условии t = 0, N = No дает функцию:

N = 112,56 ■ е^7,51°—⁴ ■ т (1)

Указаная функция - ничто иное, как математическое описание (1) скорости нарастания массы дрожжевого теста в экспоненциальной фазе.

В данном случае значение удельной скорости роста зависит от концентрации лимитирующего субстрата S (глюкозы) и эта зависимость может быть представлена в форме:

/-(S) = ^ (2)

где р_т - предельная максимальная удельная скорость роста; K_s - параметр, получивший название константы сродства субстрата (глюкозы) к микроорганизму (дрожжевым клеткам).

В настоящем исследовании это уравнение принимает форму:

7,5 ■ 10“4 ■ 5,71             "

Уравнение (2) позволяет рассчитать значение K_s- константы сродства субстрата (глюкозы) к микроорганизму (дрожжевым клеткам), равное 0,71 мин.

Впервые на зависимость скорости роста культуры от концентрации субстрата обратил внимание Моно (Корнеева, 2001), поэтому уравнение (1) получило название «уравнение Моно». По своей форме оно соответствует зависимости скорости ферментативной реакции от концентрации субстрата (уравнение Михаэлиса - Ментен). Это уравнение позволяет регулировать значение удельной скорости нарастания дрожжевой массы в зависимости от концентрации одного из важнейших компонентов питательной среды - содержания глюкозы (Полесов, Лапина, 2014).

Заключение. В работе предложены (в первом приближении) модели математического описания процессов (коллоидных, биохимических и микробиологических), протекающих при брожении полуфабрикатов на стадии экспоненциального роста.

Лапина Г.П. Кинетические модели роста дрожжевой биомассы / Г.П. Лапина // Вести. ТвГУ. Сер.: Биология и экология. 2016. № 1. С. 43-46.