Кинетические уравнения перестройки трабекулярной костной ткани в пространстве Ильюшина
Автор: Тверье В.М.
Журнал: Российский журнал биомеханики @journal-biomech
Статья в выпуске: 2 (84) т.23, 2019 года.
Бесплатный доступ
В конце XIX века Wolff отметил, что кость здорового человека или животного адаптируется к тем нагрузкам, которым подвергается. Известно, что в трабекулярной костной ткани механизм адаптации реализуется посредством выстраивания трабекул (костных балок) вдоль линий действия главных напряжений. При достижении трабекулярной тканью оптимальной структуры для определенной нагрузки в локальной области кость переходит в состояние равновесия (гомеостаза). В своих работах Cowin предложил описывать положение трабекул в каждый момент времени главными направлениями тензора структуры, отыскиваемыми из решения системы предложенных им кинетических уравнений для каждой компоненты тензора структуры. К сожалению, в настоящее время невозможно экспериментально проследить эволюцию тензора структуры in vivo , т.е. получить возможность оценить значения констант кинетических уравнений. В работе предлагается кинетическое уравнение, построенное в девиаторном пространстве Ильюшина, напрямую отражающее закон Wolff . Уравнение имеет одну материальную константу. Кинетическое уравнение согласовано с определяющим соотношением Cowin , что позволило определить не только векторные, но и скалярные свойства тензора структуры. Проведенная верификация предложенных уравнений на примере перестройки структуры для задачи всестороннего сжатия показала хорошую точность выполнения закона Wolff .
Трабекулярная (губчатая) костная ткань, тензор структуры, закон вольфа, равновесие (гомеостаз), кинетические уравнения перестройки, пространство ильюшина, векторные и скалярные свойства тензоров
Короткий адрес: https://sciup.org/146282129
IDR: 146282129 | УДК: 531/534:[57+61] | DOI: 10.15593/RZhBiomeh/2019.2.10
Текст научной статьи Кинетические уравнения перестройки трабекулярной костной ткани в пространстве Ильюшина
Закон Вольфа применительно к живой костной ткани звучит следующим образом: кость приспосабливает свою внешнюю форму и внутреннюю структуру к тем механическим силам, которые она должна выдержать [21–23].
В 1872 г. Вольф провозгласил, что «когда внешняя нагрузка в какой-либо кости изменяется вследствие травмы, патологических изменений или образа жизни, функциональная перестройка со временем переориентирует трабекулы таким образом, что они выстраиваются в линии по новым траекториям напряжения» [21–23]. В работах [14, 16, 17] обсуждался этот закон, и было установлено, что трабекулы выстраиваются по линиям главных напряжений, а математической формулировки закона Вольфа до настоящего времени нет.
В работах [14–16, 18] было предложено определяющее соотношение перестройки костной ткани. Структура описывалась с помощью тензора структуры ( fabric tensor ), входящего в определяющее соотношение как тензорная переменная наряду с тензором деформации. В работе [18] экспериментально определены материальные константы для определяющего соотношения трабекулярной костной ткани. Предложенные в работе [16] кинетические уравнения для тензора структуры были построены по тем же законам механики, что использовались для получения определяющего соотношения. Рассмотренный аналитический пример, носящий методический характер, для перестройки кости при всестороннем сжатии показал достаточную эффективность предложенных уравнений. В дальнейшем этот подход был развит в работах [7, 8, 12, 19, 20], в которых на основе разработанных постановок и алгоритмов численно был рассмотрен ряд как классических задач механики, так и задач, моделирующих перестройку костной ткани в зубочелюстной системе человека.
Однако опыт биомеханического моделирования показал ряд недостатков этого подхода:
-
1. Закон Вольфа выполняется в определяющем соотношении при сходимости в кинетических уравнениях к новому гомеостатическому состоянию.
-
2. Имеется система кинетических уравнений для каждой компоненты тензора. В каждом уравнении как минимум две материальные константы, которые необходимо уметь определять.
-
3. В настоящее время невозможно in vivo следить за историей формирования новой структуры. Единственно, что известно экспериментально: при изменении нагрузки новая структура в среднем формируется за 160 дней [16–18].
Таким образом, необходимо построить кинетическое уравнение, в которое бы входило минимальное число материальных констант.
Построение кинетического уравнения для перестройки костной ткани
Рассмотрим геометрическую интерпретацию закона Вольфа.
Трабекулярная структура костной ткани описывается симметричным положительно определенным тензором структуры Η , имеющим три положительных действительных собственных значения. Напряженное состояние определяется симметричным тензором σ , имеющим действительные произвольные собственные значения.
В произвольной декартовой системе координат поверхность Коши тензора Η представляет собой эллипсоид, полуоси которого (главные направления) наклонены к осям координат. У тензора σ в зависимости от знаков собственных значений поверхность Коши может быть эллипсоидом, однополостным или двуполостным гиперболоидом [2, 11].
Поэтому рассмотрим пространство главных напряжений [2, 11], т.е. пространство, в котором оси координат совпадают с главными осями тензора напряжений. Аналогично определяется пространство главных направлений тензора структуры Η . Если совместить эти два пространства, то в процессе нагружения для выполнения закона Вольфа необходимо совпадение главных осей тензоров напряжений и структуры.
В теории упругопластических процессов используется геометрическое представление процессов деформирования и нагружения в специальных пятимерных векторных пространствах деформации E и напряжений Σ Ильюшина [1, 3–6, 24]. Компоненты ε вектора деформации ε и компоненты σm вектора напряжении σ линейно и взаимно однозначно связаны соответственно с компонентами девиатора деформации eij и девиатора напряжений s . При этом длины векторов ε = ε и σ= σ равны соответственно интенсивностям деформации и напряжений. Таким образом, разделены векторные свойства (ориентация главных осей и угла вида соответствующих тензоров определяется направлением векторов ε и σ в построенных пространствах) и скалярные свойства напряжений и деформации. Годограф вектора ε образует в E непрерывную кривую – траекторию деформации. Траектория деформации определяет (с точностью до объемной деформации, закон изменения которой должен быть задан отдельно) всю историю деформирования. При совмещении геометрических пространств E и Σ вектор σ в каждой точке траектории определенным образом ориентирован по отношению к траектории деформации и тем самым составляет определенный угол с вектором ε . Полученные в этих совмещенных пространствах определяющие соотношения теории упругопластических процессов геометрически означают, что направление вектора напряжений в процессе деформирования меняется. Вектор σ стремится занять положение касательной к траектории деформирования. На рис. 1 показана эта ситуация при простом деформировании материала по траектории OAC с изломом в точке A.
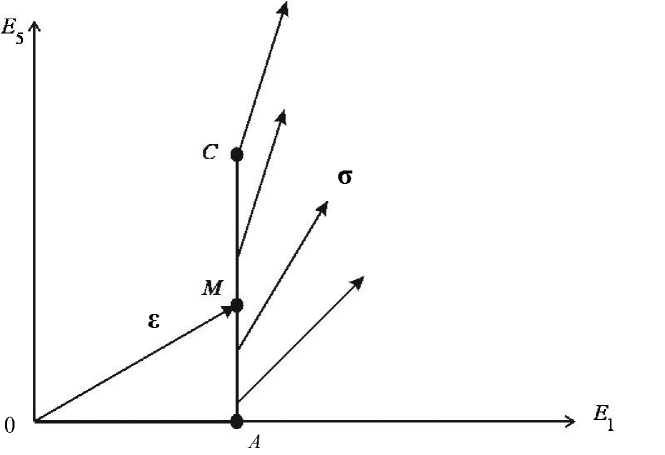
Рис. 1. Процесс деформирования материала
В процессе нагружения для выполнения закона Вольфа угол между векторами напряжений и структуры должен стремиться к нулю, так как при совпадении направлений векторов совпадут направления главных осей тензоров напряжений и структуры. Все три инварианта тензоров сохраняют свои значения при преобразованиях вращения координатных осей в точке тела физического пространства [4, 6]. Третий инвариант тензора, т.е. угол вида тензора, не сохраняет свою величину при ортогональных преобразованиях (сохраняются значения первого и второго инвариантов), соответствующих вращению и отражению траекторий в пространстве. Поэтому воспользоваться аналогами определяющих соотношений Ильюшина и его учеников не представляется возможным. В плоских задачах третий инвариант тензора не играет никакой роли (выражается через первый и второй инварианты). Но во всех вариантах определяющих соотношений вектор напряжений ложится на касательную к траектории деформации и угол между векторами определяется процессом нагружения.
Поэтому воспользуемся геометрическими основами теории упругопластических процессов для определения кинетических уравнений перестройки трабекулярной костной ткани [1, 3–6, 24]. При этом будем учитывать, что имеется определяющее соотношение для такого материала, опубликованное в работах Cowin [14–16]. Материальные константы для определяющего соотношения получены экспериментально [18]. Определяющее соотношение имеет вид
6 = 6 ( Е , Н , V ), (1)
где σ , ε – тензоры напряжений и деформации, ν – плотность костного материала. Для описания истории деформирования вводятся кинетические уравнения для Η и ν . Формулируемые кинетические уравнения для тензора структуры должны быть согласованы с уравнением (1).
Пусть построены девиаторные пространство напряжений Σ и пространство структуры H . Совместим эти пространства (рис. 2). Рассмотрим траектории нагружения средней кривизны (для двухзвенных траекторий будут выполняться аналогичные соотношения). В работах [9–10] показано, что для траекторий нагружения с большой степенью точности вектор напряжений находится в соприкасающейся плоскости траектории деформирования. Будем предполагать, что пятимерный вектор структуры η находится в соприкасающейся плоскости траектории напряжений (рис. 2).
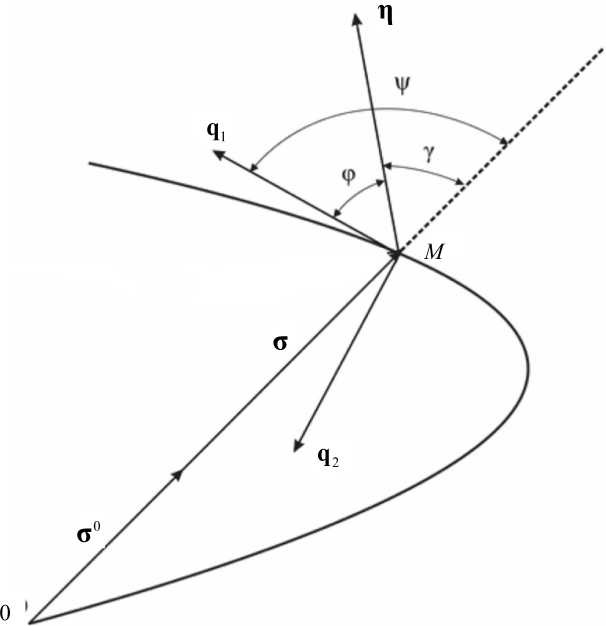
Рис. 2. Траектория напряжений и вектор структуры η : γ – угол между векторами напряжений о и структуры п ; 6 ° — единичный вектор напряжений; ф - угол между векторами структуры η и единичным вектором касательной q ; q – единичный вектор главной нормали к траектории напряжений; ψ – угол между векторами σ и q
По аналогии с постулатом изотропии Ильюшина для траекторий деформации и напряжений [1, 3–6] сформулируем следующее утверждение: ориентация вектора структуры относительно траектории напряжений зависит только от внутренней геометрии этой траектории и не зависит от ее положения в пространстве Σ. Второе предположение: векторы напряжений σ и структуры η находятся в соприкасающейся плоскости в каждой точке траектории нагружения.
В соответствии с законом Вольфа угол у между векторами напряжений — и структуры η должен стремиться к нулю с течением времени t (рис. 2), т.е.
d γ dt
= - a у.
В общем случае правая часть в кинетическом уравнении (2) является функционалом процесса нагружения. До настоящего времени экспериментально известно, что процесс перестройки заканчивается примерно за 160 дней. Это позволяет определить единственную константу в кинетическом уравнении. Поэтому в простейшем случае, имеющем ясный физический смысл, будем считать, что а = const > 0.
Уравнение (2) определяет только изменение векторных свойств тензора структуры. Необходимо построить кинетическое уравнение, описывающее изменение со временем скалярных свойств тензора структуры (длины вектора структуры п = |п|), согласованное как с определяющим соотношением (1), так и с кинетическим уравнением (2). Для этого поступим следующим образом.
Определим в каждой точке траектории напряжений М естественный репер [1, 3—6] q„ (n = 1,—,5), векторы которого определяются по длине ^ (т.е. временем нагружения t) дуги ОМ траектории напряжений и кривизнами kn (n = 1,...,5) по обобщенным формулам Френе.
Длина дуги ξ связана со временем t следующим соотношением:
^ = [ / d ^ n d 2 n dt , n = 15.
dt dt
Здесь Gn - компоненты вектора напряжений, n = 1,^,5.
Вектор структуры на основе постулата изотропии будет иметь вид
П = Pnqn, (n = 1,^,5), где P – функционалы процесса.
Так как вектор структуры η находится в соприкасающейся плоскости траектории напряжений (см. рис. 2), то получаем n = Pi qi + P2 q2, (3)
где q и q – единичные векторы касательной и главной нормали к траектории напряжений (см. рис. 2). Определим угол φ между вектором структуры η и вектором касательной qt. Пусть oo = — - единичный вектор напряжений.
σ
Функционалы P и P представим в виде
P = п cosф, P 2 =- п smф.
Пусть ψ – угол вектора σ с вектором q . Очевидно, что co = cos у q, - sinyq2, (5)
1 cosψ
-
q 2 =—:— c + Q i--- sinψ sinψ
Подставим (4), (6) в (3) и после преобразований получим
П = A o c + A i Q i ,
n sin(y - y) где A 0 = ---——-,
σ sinψ ψ = arccos ( σ , q ).
sin γ
Ai = n ---- sin ψ
.
Угол ψ определяется равенством
Теперь получим дифференциальное уравнение для изменения модуля вектора структуры η.
d σ 1 d q
Воспользуемся тем, что q, =--- , и формулами Френе q2 =-- 1,
1 dξ 2 kdξ k12
2 dq,
I d 4 )
.
Так как
oσ c = — и выполняется (5), то σ
o = o ( qx cos у - q2 sin у ).
Продифференцировав (7) по ξ , после преобразований получим
d η
— = M 1 q , + M 2 q 2 , d ξ
dA dA dA 0
где M ] = A o + ocosy-- 0 +-- 1 и M 2 = A j k - osiny---
10 d ξ d ξ2 1 1 d ξ
.
Умножим (9) скалярно на q , а затем на q . Учитывая ортогональность единичных векторов, получим
dη dη qi =M = M1, q2 =M = M2, dξ dξ
т.е.
dp ( q,-o-^ d q- = M 1 ,
dr ( q 2 • n )- n •
d q d ξ
= m2 .
I П I
Здесь q, • n = nc°s Ф и q2'П = ncos I ~ + ф I = - nsinф.
Для плоской траектории напряжений формулы Френе дают выражения
Подставим эти выражения в (10), тогда получим dηdφ cos ф - nsinф—- + kx nsinф = Mx, dξdξ11
d η d φ
--sin ф - ncosф-- + k псо8ф = M .• d ξ d ξ12
Умножим первое равенство на cos φ, а второе – на sin φ, вычтем из первого второе, тогда можно исключить скорость изменения угла наклона вектора η к касательной траектории напряжений:
d η
-- = Mx cos ф - M 2 sin ф, d ξ 12
т.е. получено кинетическое уравнение, описывающее изменение модуля вектора структуры и тем самым изменение интенсивности тензора структуры Η. Окончательно d^ = Micos(v-y)-M2 sin(v-y). (11)
d ξ
Таким образом, для решения эволюционной задачи перестройки трабекулярной костной ткани имеются определяющее соотношение (1) и кинетические уравнения (2), (11), позволяющие проследить историю формирования как структуры, так и напряженно-деформированного состояния костной ткани.
Для верификации предложенных кинетических уравнений в задаче о перестройке при всестороннем сжатии было использовано аналитическое решение
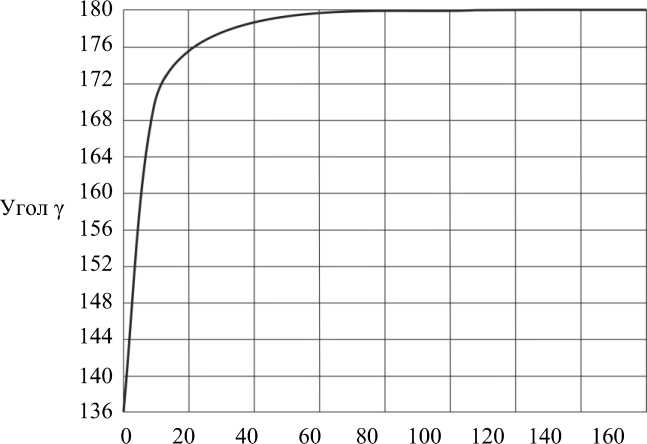
t , день
Рис. 3. Зависимость угла между векторами напряжений и структуры от времени перестройки костной ткани из работы [16]. В этом решении нагрузка сжатия плоского образца, оснащенного начальной структурой при заданной деформации, поворачивалась на 35°. Прослеживалось изменение тензора структуры. Численное решение этой задачи подробно представлено в работах [7, 8, 19, 20]. Для этого решения введены векторы напряжений σ и структуры η и построена зависимость угла γ от времени перестройки (рис. 3). Таким образом, подтверждается возможность применения предложенного кинетического уравнения (2), которое совместно с уравнением (11) может быть использовано для описания эволюции трабекулярной костной ткани.
Очевидно, что предположения, сделанные при формулировке кинетического уравнения, выполняются с хорошей точностью.
Заключение
Таким образом, построенные кинетические уравнения могут использоваться в процессе моделирования перестройки костной ткани при использовании одной материальной константы. Это дает возможность изучить историю формирования тензора структуры при различных видах нагружения.
Благодарности
Постановка задачи выполнена при финансовой поддержке РФФИ в рамках научного проекта № 18-01-00589. Результаты работы получены при финансовой поддержке правительства Пермского края.
Статья подготовлена при обучении по программе ДПО [13] в Пермском национальном исследовательском политехническом университете.
Список литературы Кинетические уравнения перестройки трабекулярной костной ткани в пространстве Ильюшина
- Васин Р.А. Определяющие соотношения теории пластичности // Итоги науки и техники. ВИНИТИ. Сер. Механика деформируемого твердого тела. - 1990. - Т. 21. - С. 3-75.
- Демидов С.П. Теория упругости: учеб. для вузов. - М.: Высшая школа, 1979. - 432 с.
- Зубчанинов В.Г. Основы теории упругости и пластичности. - М.: Высш. шк. - 368 с.
- Зубчанинов В.Г. Проблемы математической теории пластичности // Проблемы прочности. - 2000. - № 1. - С. 22-41.
- Ильюшин А.А. Механика сплошной среды. - М.: Изд-во Моск. гос. ун-та, 1990. - 310 с.


