Кинетостатическое моделирование энергоэффективного управления оборудованием с параллельной кинематикой

В работах [1-3] показано, что применительно к оборудованию с параллельной кинематикой (ОПК) могут быть реализованы оптимальные управления, повышающие эффективность выполнения на этом оборудовании некоторых технологических операций. Реализация оптимальных управлений возможна в случае, если технологическая операция не требует движения рабочего органа по всем допускаемым кинематической схемой оборудования выходным координатам. Например, для оборудования, выполненного на основе плоского трипода (рис. 1), в качестве такой технологической операции выступает фрезерование инструментом, расположенным на его под вижной платформе.

Положение платформы плоского трипода описывается тремя выходными координатами:

двумя линейными координатами полюса С в неподвижной системе координат (СК) OXY и углом

Ф, характеризующим разворот связанной с подвижной платформой СК СХ' Y ' относительно СК OXY .

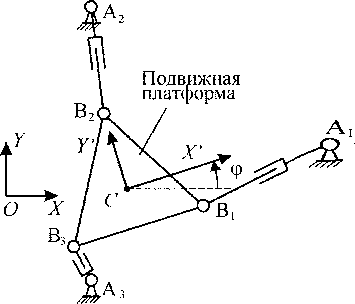
Рис. 1. Кинематическая схема ОПК на основе плоского трипода

Если продольная ось инструмента перпендикулярна подвижной платформе и проходит через полюс С, то при выполнении фрезерования достаточно обеспечить перемещение полюса С по требуемой траектории; изменение угловой координатой ф на результат выполнения этой технологической операции не влияет. Данная выходная координата в этом случае является избыточной, изменение этой координаты позволяет реализовывать оптимальные управления.

Одним из оптимальных для ОПК управлений является энергоэффективное управление, которое строится

-2

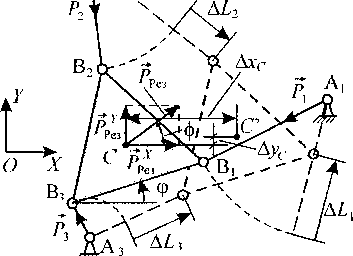
Рис. 2. Изменение длин штанг трипода при элементарном перемещении полюса подвижной платформы

из условия минимизации суммарной работы ЛПрив, совершаемой приводами станка. Реализация энергоэффективного управления приведет к экономии энергии, затрачиваемой на выполнение технологической операции.

Для анализа энергоэффективности выполнения технологических операций с использованием ОПК рассмотрим элементарное перемещение полюса С подвижной платформы плоского трипода (рис. 2) на величину Д_с = >/Ах| + Лу£ , где Дх_с, Ду_с -элементарные перемещения по направлениям осей ОХ и OY неподвижной СК OXY.

Примем, что сила резания приложена к полюсу платформы; направление этой силы задается углом ф. Уравнения вида awp\ + апрг + а\Л =-p?Q cos^;

< а_гхР_х + а^ + а₂₃Р₃ = -Р_Рез sin^;                                                     (1)

«31^Р1 ⁺ ^32^2 ^{+ а}ЗЗ^Р3 = -^Рез (*С ^sin Ф ~ У С ^cos Ф\ составляющие статическую модель рассматриваемого устройства, позволяют определить силы реакций Р , возникающие в штангах под действием силы резания. Здесь х_с, у_с - текущие координаты полюса С подвижной платформы в СК OXY; коэффициенты а_у описаны в [1].

При элементарном перемещении полюса подвижной платформы на величину Д_с штанги изменят свои длины на величины \Lj , характеризуемые направлением. Так как силы реакций Pj всегда направлены вдоль продольных осей соответствующих штанг, то элементарная работа этих сил

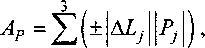
7=1

где знак «+» соответствует случаю, когда направление силы реакции в у-й штанге совпадает с направлением изменения длины этой штанги. Очевидно, что элементарная работа реакций в штангах будет равна элементарной работе внешних силовых факторов (силы резания), определяемой для рассматриваемой задачи как

^Внеш = ^С^Рез ^COS Ф ⁺ ^С^Рез ^sin Ф •

Элементарная работа, совершаемая приводом у-й штанги, должна рассматриваться как величина положительная, так как понятие «отрицательная работа» не применимо к устройству (двигателю, приводу), способному только потреблять энергию из какого-либо источника. Поэтому выражение для суммарной работы приводов, изменяющих длины штанг, будет иметь следующий вид:

з

^Прив = У^АЛЛ! 1

7=1

Работа приводов ЭПрив является величиной положительной; для удобства ее сравнения с работой внешних силовых факторов введем в рассмотрение положительно определенную величину

А IЛ I

Петр I Внеш | ’ которую назовем потребной работой. В общем случае будет выполняться условие

^Прив - ^Потр ’ так как потребная работа представляет собой теоретический минимум работы, которая должна совершаться приводами при перемещении подвижной платформы при заданном внешнем нагружении.

На рис. 3 показано, как изменяется потребная работа при различных направлениях силы резания. Моделирование проводилось при Ахс = Аус =0,1 мм, РРез =1000Н; угол разворота подвижной платформы <^ = 15° при моделировании оставался постоянным. Равенство потребной работы нулю наблюдается в случаях, когда сила резания перпендикулярна элементарному перемещению платформы.

На этом же рисунке показана работа приводов, обеспечивающая перемещение подвижной платформы на указанное выше элементарное перемещение при действии переменной по направлению силы резания. Графики подтверждают, что потребная работа не превышает работу приводов. При равенстве потребной работы нулю работа приводов, обеспечивающая перемещение подвижной платформы, нулю не равна, так как сила резания все равно создает в штангах усилия, которые должны преодолеваться приводами.

Третий график на рис. 3 соответствует реализации рассматриваемого элементарного перемещения при использовании станка традиционной компоновочной схемы: принято, что станок имеет два привода, обеспечивающие перемещения по ортогональным координатам, сонаправ-ленным осям ОХ и ОУ СК ОХУ. Анализ графиков показывает, что станок, выполненный на основе рассматриваемого плоского трипода, потенциально способен выполнять технологические операции с меньшими затратами энергии, чем станок традиционной компоновки.

Рассмотрим, как будет изменяться работа приводов станка, выполненного на основе трипода, при реализации рассматриваемого перемещения платформы для различных значений координаты (р. Результаты моделирования представлены на рис. 4, из которого видно, что для каждого направления силы резания можно найти значения угла ф, обеспечивающего минимум работы приводов на рассматриваемом элементарном перемещении. В общем случае можно ставить задачу уменьшения работы, совершаемой приводами на каждом элементарном перемещении платформы при выполнении некоторой технологической операции:

з

^Прив (^) = ^ I А^у Wj (^)| -> min .

7=1

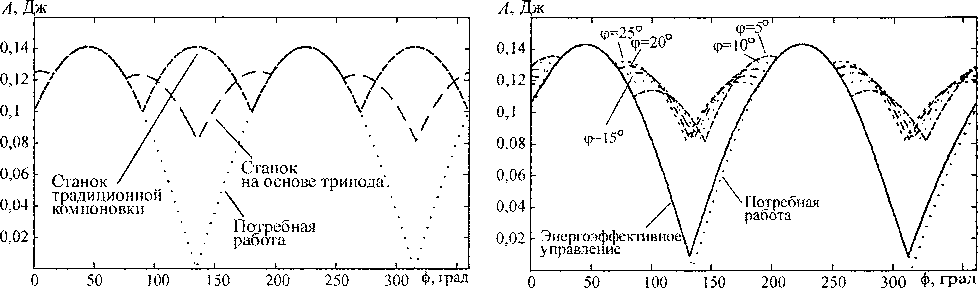
Рис. 3. Моделирование работы на элементарных       Рис. 4. Изменение работы приводов при различных перемещениях                     значениях угла ф поворота подвижной платформы

Задача решается за счет изменения координаты ф, от которой зависят как изменения длин штанг XLj {ф), так и возникающие в них усилия Pj (ср).

На практике часто применяют ОПК, построенное по гексаподной схеме (рис. 5). В таком оборудовании за счет изменения длин штанг Lj = |А_уВ_у|, / = 1...6, рабочий орган способен совершать движения по шести выходным координатам: трем линейным и трем угловым. Примем в качестве выходных угловых координат три угла Крылова (у/, 5, у), определяющие разворот рабочего органа в неподвижной системе координат OXYZ [4]. Для некоторых технологических операций, например, при фрезеровании инструментом со сферической режущей частью, выходные угловые координаты могут использоваться для реализации энергоэффективного управления, при котором должно обеспечивать выполнение условия

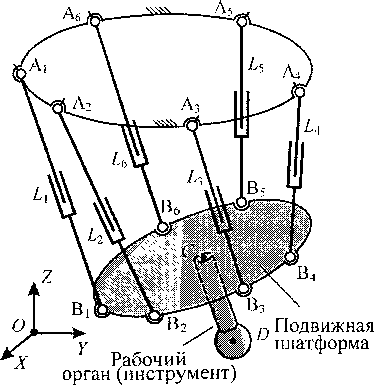
Рис. 5. Кинематическая схема ОПК, обеспечивающего движение рабочего органа по шести координатам

^Прив <УЛ ^ У) = X \^ ^’ ^S’ ^^PJ ^’ ^S’ Л ^ ^min    <²>

7=1

для каждого элементарного перемещения рабочего органа.

На рис. 6 показаны результаты моделирования энергоэффективного управления при движении рабочего органа некоторой технологической машины, выполненной по гексаподной схеме, по заданной траектории. Траектория определяется линейным во времени изменением координаты yD точки D, являющейся центром сферической части инструмента (см. рис. 5), при неме-няющихся остальных линейных координатах этой точки. Выходные угловые координаты при моделировании оставались постоянными или изменялись в соответствие с условием (2) с целью реализации энергоэффективного управления.

Уменьшение работы приводов при моделировании рассматриваемого оптимального управления (эффективность управления) составило «1 б %;

уменьшение достигнуто за счет изменения выходных угловых координат по законам, показанным на рис. 6, б.

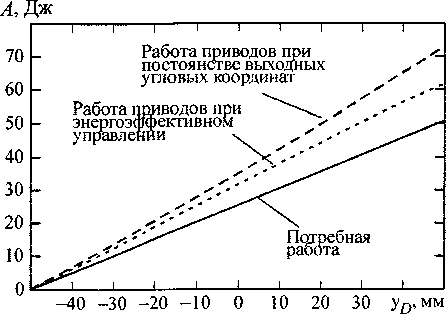
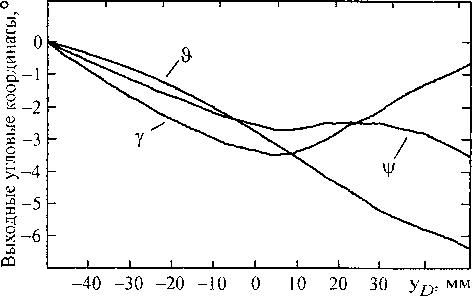
Рис. 6. Моделирование энергоэффективного управления с использованием статической модели: а - графики работ; б - законы изменения выходных угловых координат при энергоэффективном управлении

Рабочий орган и другие подвижные элементы реального оборудования обладают массоинерционными параметрами, следовательно, для более точного моделирования энергоэффективного управления необходимо использовать кинетостатическую модель ОПК, например, описанную в [5].

В процессе работы реального оборудования усилия приводов будут определяться как внешними силовыми факторами (статическая составляющая), так и силами инерции (динамическая составляющая). Статическая составляющая определяется зависимостями, аналогичными (1). Динамическая составляющая для модели, описанной в [5], зависит от массоинерционных параметров элементов оборудования и вторых производных по времени от его обобщенных координат, в качестве которых выступают длины штанг. Работа, совершаемая приводами, также будет иметь две составляющие: статическую и динамическую.

Реализация энергоэффективного управления предполагает постоянное изменение выходных угловых координат в процессе формирования траектории движения рабочего органа, что вызовет увеличение вклада в работу приводов динамической составляющей. Увеличение скорости движения рабочего органа потребует увеличения скорости изменения выходных угловых координат, что приведет к еще большему возрастанию вклада динамической составляющей, т. е. все большая часть работы, совершаемой приводами, будет направлена на обеспечение ускоренного (замедленного) перемещения элементов ОПК, главным образом - подвижной платформы и рабочего органа, для реализации энергоэффективного управления. Можно предполагать, что с увеличением скорости движения рабочего органа эффективность рассматриваемого оптимального управления будет снижаться.

Для оценки эффективности выполнено кинетостатическое моделирование движения точки D по траектории, аналогичной принятой при статическом моделировании. Под эффективностью, как и ранее, понимается снижение работы приводов в сравнении с управлением, при котором выходные угловые координаты остаются неизменными. Массоинерционные параметры, используемые при кинетостатическом моделировании, получены с использованием пакета SolidWorks для упрощенной твердотельной модели ОПК.

Кинетостатическое моделирование проводилось для различных скоростей движения точки D рабочего органа; внешние силовые факторы принимались не зависящими от скорости рабочего органа. Результаты моделирования приведены в табл. 1. Анализ результатов подтверждает предположение, что с увеличением скорости будет наблюдаться снижение эффективности рас- сматриваемого оптимального управления.

С уменьшением скорости эффективность возрастает и стремится к значению, полученному при статическом моделировании. Можно предположить, что для относительно невысоких скоростей движения рабочего органа ОПК реализация энергоэффективного управления может строиться с использованием только статической модели механизма, лежащего в основе этого оборудования. Данное предположение подтверждается сравнением законов изменения выход

Таблица 1

vD, мм/с	Эффективность, %
0,1	15,2
1,0	14,8
10	13,9
20	7,9
50	1,7

ных угловых координат, обеспечивающих энергоэффективное управление, полученных при статическом (см. рис. 6, б) и кинетостатическом моделировании для Vp =10 мм/с и vD =1,0 мм/с (рис. 7): с уменьшение скорости законы изменения выходных угловых координат, обеспечивающие энергоэффективное управление, приближаются к аналогичным законам, полученным при статическом моделировании.

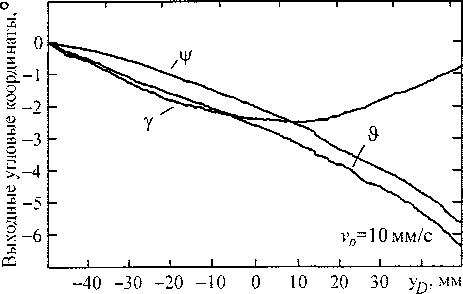
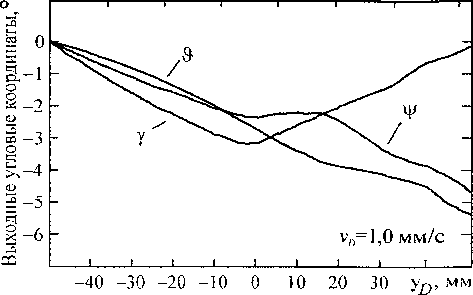
Рис. 7. Законы изменения выходных угловых координат, полученные при кинетостатическом моделировании

В табл. 2 представлены результаты моделирования поведения рассматриваемого ОПК с использованием кинето-статической модели при условии, что выходные угловые координаты изменяются по законам, полученным при статическом моделировании (см. рис. 6, б). Из таблицы видно, что в некотором диапазоне скоростей управление, построенное на основе результатов статического моделирования, обеспечивает уменьшение работы приводов, сопоставимое с получаемым при энергоэффективном управлении (см. табл. 1). С увеличением скорости расхождения в результа-

Таблица2

vD , мм/с	Эффективность, %
0,1	14,8
1,0	13,5
5,0	10,2
7,5	4,6
9,0	2,7
10,0	2,0

тах возрастают. Следовательно, в некотором диапазоне скоростей рабочего органа при построении энергоэффективного управления оборудованием можно отказаться от использования кинето-статической модели, что существенно упростит расчеты. Диапазон таких скоростей должен уточняться для конкретной модели ОПК. При более высоких скоростях использование кинето-статической модели обязательно.