Классификация сумм

Если взять любую сумму, то все остальные суммы можно разделить на три группы: одинаковые суммы, суммы разложения и другие суммы. Критериями классификации являются слагаемые и результат сложения.

Одинаковые суммы

Одинаковые суммы объединяются в отдельную группу свойством коммутативности [1, стр.41]. Суммы из этой группы имеют попарно одинаковые по величине слагаемые и равное количество слагаемых. Результат сложения этих сумм одинаковый.

Пример одинаковых сумм приведен на рис.1.

1+2+3+4=103+2+4+1=102+4+1+3=10

Puc.l Одинаковые суммы

Количество сумм в данной группе определяется количеством слагаемых. Для бесконечных сумм оно равно бесконечности.

Суммы разложения

Если результаты сложения разного количества слагаемых или разных по величине слагаемых одинаковые, то такие суммы образуют группу разложения (рис.2).

6 + 4 = 10

2 + 8 = 10

3 + 2 + 5 = 10

1 + 1 + 2 + 2 + 4 = 10

1+1+1+1+1+1+1+1+1+1=10

Puc.l Суммы разложения

Любую из этих сумм можно получить разложением результата сложения на слагаемые при помощи линейных угловых функций [2, стр.64]. Получив при этом два слагаемых, любое из них можно также разложить на слагаемые и так далее. Пример разложения для первых трех сумм показан на рис.3.

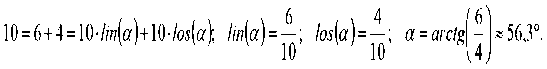
io=2+8=ioN/?)+ioN$ *^ ^ P=arctfc

«14°.

10 = 3+7 = 3+(2+5)=107т(/)+10'/о5(/)'(/ш(д')+/от(<7))=107т(/)+107(«(^^^

Mz)=^ h(z)=^; Z=^k k23,2°;

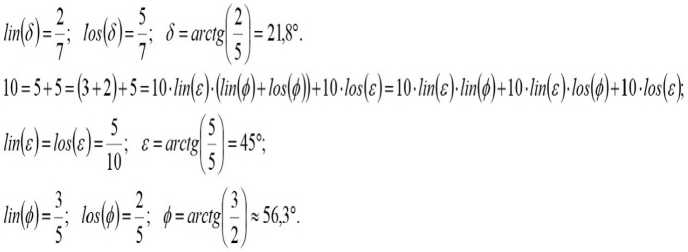
РисЗ Разложение на слагаемые

Пример разложения числа на три слагаемых показывает, что разные варианты разложения могут давать одну и ту же сумму, что лежит в основе ассоциативных свойств сложения. Чем больше слагаемых содержит сумма, тем больше различных вариантов разложения может быть. Разложение на слагаемые можно продолжать до бесконечности. Разные углы и разные алгоритмы разложения позволяют получить разные варианты бесконечных сумм. Теория пределов позволяет определить результат сложения на основе анализа слагаемых. Разложение на слагаемые позволяет результат суммирования представить в виде бесконечного ряда слагаемых.

Для примера разложим единицу в бесконечную сумму по следующему принципу: разложение выполняется под углом 45°, каждое второе слагаемое раскладывается на два слагаемых (рис.4).

2 2

2 2 2 2 2 2

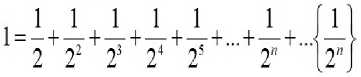
РисА Разложение на бесконечное количество слагаемых

В фигурных скобках указана сумма невидимой компенсирующей группы слагаемых [3, стр.41], дополняющая результат сложения до целой единицы. Можно предположить, что любая сумма, даже бесконечный расходящийся ряд, в тригонометрическом виде равна единице.

Если результат сложения любой суммы отличается от результата сложения рассматриваемой суммы, то эта сумма не имеет никакого отношения к рассматриваемой сумме и относится к группе

«другие суммы».

Предположим, что для суммы a +b=c существует другой результат сложения d , не равный с . То есть, a+b=d . Представим эти два выражения с использованием линейных угловых функций, а затем переведем их в тригонометрический вид (рис.5).

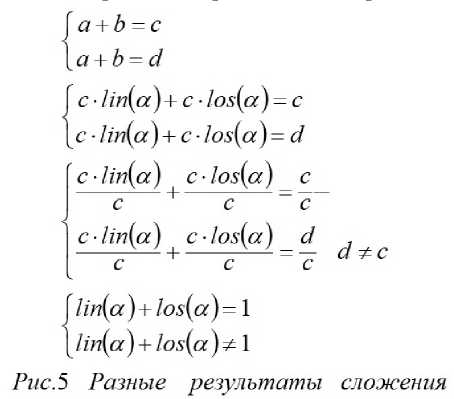
Предположение о наличии разных результатов сложения у одной и той же суммы выводит нас за пределы математики, где основные тригонометрические соотношения перестают работать (рис.6).

lin(o!) + los^a^ 1

sin2 (a) + cos2 (c?)^ 1 tg(,a)-ctg(a^\

Рис.6 За пределами математики

Почему одна и та же сумма слагаемых не может иметь двух разных результатов сложения? Понять это можно, рассмотрев обратный процесс – превращение тригонометрических функций в конкретные математические суммы. Более подробно мы рассмотрим это в отдельной публикации.

В завершение разговора о наличии двух разных результатов сложения у расходящихся рядов, я приведу пример из физики. В земной коре ( сходящийся ряд [4]) существуют природные пещеры ( сумма сходящегося ряда ). Используя специальные механизмы ( сходимость по Чезаро и др. ) мы можем получить искусственные тоннели ( сумма сходящегося ряда ). В морях и океанах ( расходящийся ряд ) нет природных пещер ( сумма ряда отсутствует ). Применение специальных механизмов ( сходимость по Чезаро и др. ) позволяет нам получить искусственные тоннели ( сумма расходящегося ряда ) в водной толще. На основании этой, математически доказанной, теории можно спроектировать сеть тоннелей для автомобильных и железных дорог, опоясывающих всю земную поверхность. Такая теория вполне возможна, если мы не понимаем различия между твердыми телами ( сходящийся ряд ) и жидкостями ( расходящийся ряд ).

Не существует математических методов, позволяющих получить другой результат сложения для рассматриваемой суммы.