Классификация узлов в утолщенном торе, минимальные диаграммы которых не лежат в кольце и имеют пять перекрёстков
Бесплатный доступ
Построена таблица узлов в утолщенном торе TxI, минимальные диаграммы которых не лежат в кольце и имеют пять перекрестков.
Узел, утолщенный тор, таблица узлов
Короткий адрес: https://sciup.org/147158760
IDR: 147158760 | УДК: 515.162.3
Текст научной статьи Классификация узлов в утолщенном торе, минимальные диаграммы которых не лежат в кольце и имеют пять перекрёстков
Введение F×I, F –-
,.
-
S3 T×I, T = S1 ×S1 –
. T×I-
, .-
: .-
[1, 2]-
-
[3] .[4].
,[5],
. ..-
.
Основной результат ( . .)
. K ⊂ T×I-
G ⊂ T 4, «»
, . K-
( ),-
, – t ⊂ I.-
, .-
,
.
-
1. K , (-
- ) ,K.
G ⊂ T ,-
.
, .. ,-
. ,-
T×I,
-
[6] . , ,-
- T.,
, [3].-
, ,.
.
-
1. 69 T×I,-
- .. 1.
1-
, [5].-
-
5 , – 5,
, – .-
Акимова А .А. Классификация узлов в утолщенном торе, минимальные диаграммы которых не лежат в кольце и имеют пять перекрёстков
. , T×I
. [7, 8].

Рис. 1. Диаграммы с 5 перекрестками узлов на торе T, не лежащие в кольце.
Top T представлен в виде квадрата с отождествленными противоположными сторонами
Перечисление графов и проекций
, T×I, ,-
.
-
1. 6-
- , (. 2).
-
2. 34T×I,
1-
2[5], n 4.
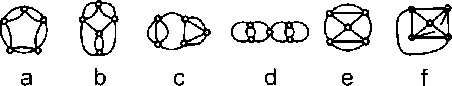
Рис. 2. Регулярные графы степени 4 с пятью вершинами, не имеющие петель
5 , (. 3).
Математика
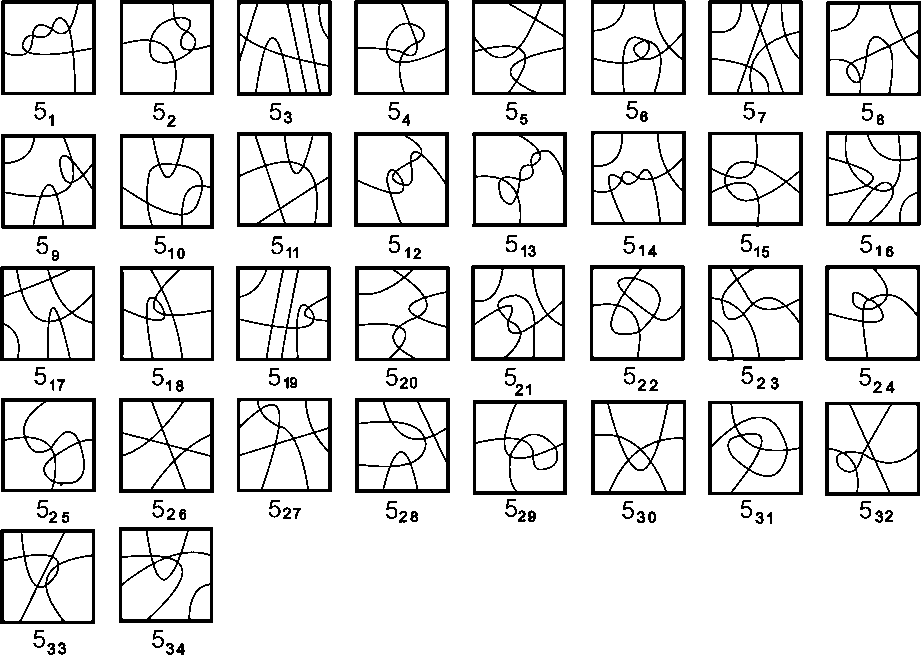
Рис. 3. Проекции с 5 перекрестками узлов на торе T, не лежащие в кольце.
Top T представлен в виде квадрата с отождествленными противоположными сторонами
2 2[5], n 4.
, 2 ( . . 3),T, -
. n2
32 . ,-
-
[5] . , . , ,-
- .,
,,
.
Различность всех приведенных в таблице узлов доказывается с помощью вычисления их [7, 8].:
X (K) = ( - a ) - 3 ω (K) ∑ aα ( s ) - β ( s ) ( - a 2 - a - 2 ) γ ( s ) xδ ( s ) , s
-
(s ) (s) – A B s, (s) (s) –-
- ,,
s . , ,
.
. , ,. 1,
. 34 ,-
Заключительные замечания
-
1. 5 : 5 21 , 5 22 , 5 56 –5 58 .
-
2. 13 : 56, 512, 513, 517, 521 , 531, 544, 546,
-
3. , , 6.
5
3
5
7
.
5 49 , 5 51 , 5 53 , 5 56 , 5 68 .
Акимова А .А. Классификация узлов в утолщенном торе, минимальные диаграммы которых не лежат в кольце и имеют пять перекрёстков Литература
. . // . :,
, . – 2012. – . 12. – . 3. – C. 10–21.
P. 395–407.
CLASSIFICATION OF KNOTS IN THE THICKENED TORUS WITH MINIMAL DIAGRAMS WHICH ARE NOT IN A CIRCULE AND HAVE FIVE CROSSINGS
A.A. Akimova 1
Список литературы Классификация узлов в утолщенном торе, минимальные диаграммы которых не лежат в кольце и имеют пять перекрёстков
- Дроботухина, Ю.В. Аналог полинома Джонса для зацеплений в RP3 и обобщение теоремы Кауфмана-Мурасуги/Ю.В. Дроботухина//Алгебра и анализ. -1990. -Т. 2, № 3. -С. 171-191.
- Drobotukhina, Yu.V. Classification of links in RP3 with at most six crossings/Yu.V. Drobotukhina//Advances in Soviet Mathematics. -1994. -V. 18, № l. -P. 87-121.
- Gabrovshek, B. Knots in the solid torus up to 6 crossings/B. Gabrovshek, I.M. Mroczkowski//J. Knot Theory Ramifications. -2012. -V. 21, -1250106. [43 c.] DOI: 10.1142/S0218216512501064
- Enumerating the k-tangle projections/A. Bogdanov, V. Meshkov, A. Omelchenko, M. Petrov//J. Knot Theory Ramifications. -2012. -V. 21, № 7. -1250069. [17 c.] DOI: 10.1142/S0218216512500691
- Акимова, А.А. Классификация узлов малой сложности в утолщённом торе/A.A. Акимова, С.В. Матвеев//Вестник Новосибирского государственного университета. Серия: Математика, механика, информатика. -2012. -Т. 12. -Вып. 3. -С. 10-21.
- Matveev, S.V. Prime decompositions of knots in T х I/S.V. Matveev//Topology and its Applications. -2012. -V. 159, № 7. -C. 1820-1824 DOI: 10.1016/j.topol.2011.04.022
- Kauffman, L. State models and the Jones polynomial//Topology. -1987. -V. 26, № 3. -P.395-407.
- Прасолов, В.В. Узлы, зацепления, косы и трёхмерные многообразия/В.В. Прасолов, А.Б. Сосинский. -М.: МЦНМО, 1997. -352 с.


