Классификация узлов в утолщенном торе, минимальные октаэдральные диаграммы которых не лежат в кольце

Задача табулирования является центральной проблемой теории узлов. Тенденция к развитию теории узлов в трехмерных многообразиях, отличных от трёхмерной сферы S³, наблюдающаяся в последние годы, привела к задаче табулирования глобальных узлов. Мы рассматриваем продолжение классической теории узлов в S 3 на случай узлов в утолщенном торе T х I, как в одном из самых простых трёхмерных многообразий после S 3 . Узлы в T х I можно задавать диаграммами на T, аналогичными сферическим диаграммам классических узлов. При этом роль преобразований Рейдемайстера сохраняется: они реализуют изотопии узлов. Из немногих работ по табулированию узлов в других многообразиях упомянем работы [1, 2] по узлам в проективном пространстве и [3] по узлам в полном торе. Эффективный метод табулирования тэнглов описан в [4]. Таблица виртуальных узлов представлена в [5]. Настоящая статья продолжает исследование, начатое в работах [6, 7].

Автор выражает благодарность профессору С.В. Матвееву за постановку задачи и помощь в её решении.

• 1.    Основной результат

Будем рассматривать узлы (т.е. простые замкнутые кривые) в T х I с точностью до эквивалентности в смысле гомеоморфизма. Проекция G узла K с T х I представляет собой регулярный граф G с T степени 4, для которого прохождение вершин по правилу «прямо вперед» определяет полный обход, отвечающий узлу. Диаграмма D узла K получается из этого графа указанием (путем разрывов обхода), какой из проходящих через каждую вершину участков узла расположен выше, какой - ниже другого в смысле величины координаты t с I. Две проекции считаются эквивалентными, если одна получается из другой гомеоморфизмом T на себя. Эквивалентность диаграмм имеет тот же смысл, но дополнительно разрешается одновременно изменять типы всех перекрестков.

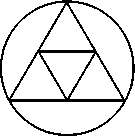
Определение 1. Диаграмма D узла K называется минимальной, если ее сложность (число перекрестков) не превосходит сложности    Рис. 1. Граф «октаэдр»

любой диаграммы каждого узла, эквивалентного узлу K. Проекция

G с T называется минимальной, если минимальна хотя бы одна из отвечающих ей диаграмм.

Мы будем рассматривать только те узлы в T х I, которые не лежат в утолщенном кольце. Поэтому мы не включаем в таблицу узлы, минимальные диаграммы которых можно расположить в некотором кольце на T. Дело в том, что такие узлы близки к узлам в полном торе, табулирован- ным в [3]. Заметим также, что мы не рассматриваем локальные узлы, потому что они являются уже табулированными узлами в S3.

Следующая теорема является основным результатом статьи.

Теорема 1. Существуют ровно 53 различных узла в T х I, минимальные диаграммы которых не лежат в кольце и соответствуют графу «октаэдр», представленному на рис. 1. Эти диаграммы изображены на рис. 2.

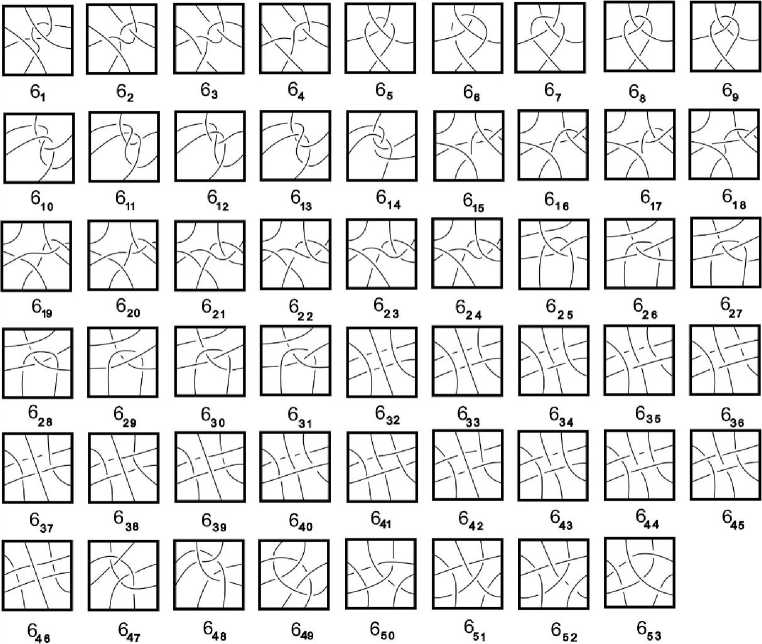
Рис. 2. Диаграммы с 6 перекрестками узлов на торе Т, не лежащие в кольце и отвечающие графу типа «октаэдр». Тор T представлен в виде квадрата с отождествленными противоположными сторонами

Доказательство теоремы 1 состоит из четырех частей и аналогично доказательству соответствующей теоремы, подробно описанному в [6]. Сначала мы перебираем все минимальные проекции с 6 перекрестками на торе T, имеющие октаэдральный тип и не лежащие в кольце, затем – соответствующие им минимальные диаграммы. При этом дубликаты отбрасываются. На последнем этапе мы доказываем, что отвечающие этим диаграммам узлы в T х I различны. В качестве инварианта мы используем обобщенную скобку Кауфмана [8, 9].

333339 333348 333348 333357 333456 334446 334446 334455

®1       62       63       6₄      65      6₆      67 6s

Рис. 3. Проекции узлов на торе T, не лежащие в кольце и соответствующие графу «октаэдр». Каждая строка { i 1 , i 2 … i 6 } означает, что дополнение к данной проекции есть набор из i m -угольников, где 1 ≤ m ≤ 6

Шаг 1. Предположим, что T\G' - дополнение к G' на T - содержит пятиугольную грань P .

Шаг 1.1. Покажем, что вершины P различны и соединены между собой ещё тремя ребрами G' .

Акимова А.А.

Рассмотрим пятиугольник P на T. Отождествление его смежных вершин допустимо при наличии петли в графе, соответствующем G', а несмежных – при наличии кратных ребер, в то время как граф «октаэдр» не содержит этих элементов. Поэтому все вершины P различны (т.е. P – вло- женный) и имеют валентность 2.

Оставшаяся шестая вершина N графа, как любая его вершина, имеет валентность 4. Поэтому N соединена четырьмя (в силу отсутствия петель) ребрами с разными (из-за отсутствия кратных ребер) вершинами P. Предположим, что это соединение уже проведено некоторым образом. То- гда P имеет 1 вершину валентности 2 и 4 вершины валентности 3, в то время как все вершины должны иметь валентность 4. Легко видеть, что вершины P необходимо соединены между собой ещё тремя ребрами G'.

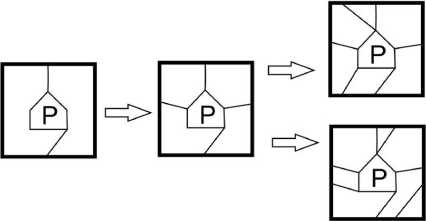
Рис. 4. Способы последовательного добавления трех ребер к пятиугольной грани P на T

Шаг 1.2. Следовательно, построение G' можно начать с рассмотрения вложенного пятиугольника P на T и соединения вершин P ещё тремя ребрами таким образом, чтобы P содержал 1 вершину валентности 4 и 4 вершины валентности 3 (комбинация валентностей согласована с последующим соединением P с шестой вершиной N ). Новые ребра соединяют только несмежные на момент добавления ребра вершины, потому что граф не содержит кратных рёбер. В силу симметрии способ добавления первых двух ребер определяется единственным образом.

Третье ребро можно добавить двумя различными способами, см. рис. 4. Имеем фрагмент проек- ции G'', содержащий 5 вершин и 8 ребер.

Очевидно, что T\ G'' состоит из 3 дисков. Шестая вершина N проекции G' может находиться в любом из этих дисков, кроме P . Способы проведения оставшихся ребер определяются единственным образом для каждого из возможных вариантов подходов ребер к вершинам пятиугольной грани. Получаются проекции 6 4 , 6 5 и 6 8 .

Шаг 2. Предположим, что T\G' не содержит пятиугольной грани. В таком случае T\G' включает, по крайней мере, 3 либо треугольных, либо четырехугольных грани, что можно проверить, непосредственно перечислив все возможные комбинации числа углов в гранях.

Рис. 5. Варианты взаимного расположения трех треугольных граней на T так, что общее число их вершин ≤ 6

Шаг 2.1. Предположим, что T\G' содержит 3 треугольные грани. Все они вложенные, потому что граф не содержит петель и кратных ребер. Все четыре варианта взаимного расположения треугольных граней так, что общее число их вершин ≤ 6, показаны на рис. 5.

Рассмотрим вариант I.

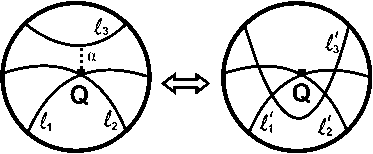
Рис. 6. Операция добавления трех треугольных граней

Определение 2. Пусть проекция G ⊂ T и диск D ⊂

T таковы, что G пересекает D по трем собственным дугам

• l 1 ,    l 2 , l 3 ⊂ D , причем l 1 пересекает l 2 трансверсально в одной точке Q , а l 3 не имеет общих точек с l 1 и l 2 . Тогда операция добавления трех треугольных граней состоит в замене дуг l 1 , l 2 , l 3 ⊂ D на

  три

  
  

новые дуги

l 1 ' , l 2 ' , l 3 ' ⊂ D , которые имеют те же концы и, помимо Q , ещё 4 трансверсальные точки пересечения дуги l 3 ' поочередно с дугами l 1 ' и l 2 ' .

Для выполнения этой операции достаточно выбрать простую дугу α ⊂ T , соединяющую вершину Q ⊂ G с точкой на ребре G , а в качестве диска D взять регулярную окрестность этой дуги, см. рис. 6. Обратная операция, то есть замена дуг l 1 ' , l 2 ' , l 3 ' ⊂ D на дуги l 1 , l 2 ,l 3 ⊂ D, называется устранением трех треугольных граней .

Операция добавления трех треугольных граней увеличивает число перекрестков проекции на 4. Таким образом, чтобы получить G' с 6 перекрестками, содержащую фрагмент, показанный на рис. 6 справа, достаточно рассмотреть все проекции G'' на торе с 2 перекрестками и применить указанную операцию, выбрав дугу α так, чтобы T\G'' U α содержало только дисковые компоненты. Имеем проекции 6₁ – 6₅ , см. рис. 7.

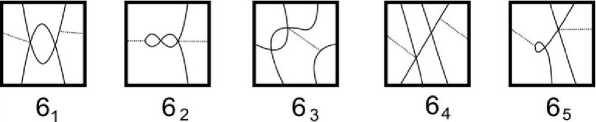
Рис. 7. Получение проекций 6 1 –6 5 операцией добавления трех треугольных граней

Рассмотрим варианты II и III.

Покажем, что G' , содержащая фрагмент II или III, обязательно содержит и фрагмент I.

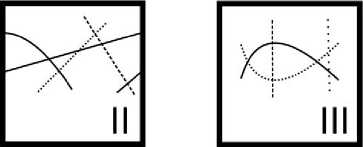
Рис. 8. Нити, из которых составлены фрагменты проекций вариантов II и III

Действительно, фрагменты II и III состоят из, соответственно, 3 и 4 нитей (на рис. 8 они показаны разными типами линий). Для получения G' эти нити нужно соединить в одну. Мы соединяем концы, окрашенные в разные цвета, иначе восстановится проекция зацепления.

Ребро, соединяющее два конца, может проходить

• 1)    нетривиально, т.е. изменять типы компонент T\G' ,

• 2)    тривиально.

Легко видеть, что соединение пары концов ребром, проходящим тривиально, приводит к созданию петли, кратного ребра или фрагмента I. Следовательно, новое ребро нужно проводить нетривиальным образом, 3 и 4 раза соответственно, в то время как на торе возможно только 2 раза, а в кольце, в котором уже лежит фрагмент II – только 1.

Рассмотрим вариант IV.

Очевидно, что T\G' содержит кольцевую компоненту.

Шаг 2.2. Предположим, что T\G' содержит 3 четырехугольные грани. Любые две из них имеют пару общих вершин, в силу того, что все три грани имеют 12 вершин, в то время как граф

– только 6. На рис. 9 (I–III) четырехугольные грани имеют общее ребро, рис. 9 (IV) – только общие вершины. Рассмотрим эти случаи:

Рис. 9. Способы расположения трех четырехугольных граней

• I.    Восстанавливается либо проекция зацепления, либо проекция, содержащая двойные ребра или петли, см. рис. 10.

  

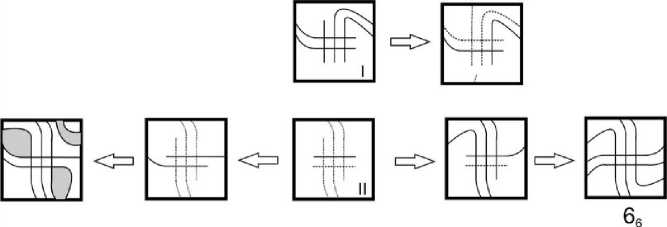
  Рис. 10. Восстановление проекций в случаях I и II

  
  

Акимова А.А.

• II.    Восстанавливается проекция 6 6 или проекция узла, имеющая двойное ребро, см. рис. 10.

• III.    Очевидно, что T\G' содержит кольцевую компоненту.

• IV.    Уже построена проекция 6 7 .

• 3. Доказательство теоремы 1

Покажем, что все проекции на рис. 3 действительно различны. Посчитаем количество углов в каждом из 6 многоугольников, составляющих T\G' . Наборов таких чисел достаточно, чтобы различить любые две проекции на рис. 3, за исключением пар (6 2 , 6 3 ) и (6 6 , 6 7 ). Проекции (6 2 , 6 3 ) различны, потому что в первом случае одна из треугольных граней имеет по одному общему ребру с каждой из трёх других, а во втором – нет. Проекции (6₆, 6₇) различны, потому что в первом случае треугольные грани имеют общее ребро. Теорема 2 доказана.

Восстановим по проекциям, указанным в теореме 2 (см. рис. 3), диаграммы узлов на T, выбрав тип каждого перекрестка. Для проекции с n вершинами это можно сделать 2 ⁿ , то есть в нашем случае 64, способами. Однако для каждой проекции достаточно рассмотреть 32 случая, поскольку тип одной вершины можно зафиксировать благодаря симметрии T × I (тип узла не меняется при одновременной смене типов всех перекрестков диаграммы на противоположный).

Различность всех приведенных в таблице узлов доказывается с помощью вычисления их обобщенных скобок Кауфмана [6, 8, 9]. Точная формула такова:

X ( K ) ₌ ( _- a ) - 3 ω ( K ) _∑ a α ( s ) - β ( s ) ( _- a 2 _- a - 2 ) γ ( s ) x δ ( s ) , где α ( s ) и β ( s ) – числа сглаживаний типа A и B в состоянии s , а γ ( s ) и δ ( s ) – числа тривиальных и нетривиальных окружностей на торе, полученных в результате сглаживания всех перекрестков, которое соответствует состоянию s . Разумеется, сумма берется по всем возможным состояниям, а ω ( K ) обозначает число скручивания диаграммы.

Все полиномы оказались различными. Отсюда следует, что все узлы, приведенные на рис. 2, различны. Попутно мы получаем доказательство минимальности каждой из 8 проекций, указанных в теореме 2.