Классификация выпуклых многоугольников

два класса: ординарные и особенные.

Рис. 1

Введем обозначения и соглашения, которых будем придерживаться на протяжении статьи. Выпуклый многоугольник, разбиение которого мы будем изучать, назовем исходным . Число сторон исходного многоугольника обозначим n . Многоугольники, на которые разбивается исходный многоугольник диагоналями, будем называть элементарными . Назовем выпуклый многоугольник ординарным , если никакие три диагонали не пересекаются в одной точке внутри многоугольника. В противном случае будем называть многоугольник особенным . Точку внутри особенного многоугольника, в которой пересекаются k+2 диагоналей, будем называть особенностью или полюсом порядка k . Очевидно, что порядок особенности не может быть больше m = |_ и /2 J - 2 . В частности, при n < 6 многоугольник не может иметь особенностей. А при каждом n ≥ 6 выпуклые n-угольники можно разбить на

Пусть n ≥ 6. Количество особенностей порядка k будем обозначать через s_k. Упорядоченный набор χ = (s₁, s₂, …, s_m) назовем характеристическим вектором исходного многоугольника. Например, у семиугольника, изображенного на рис. 1, три полюса первого порядка (X, Y и Z). Соответственно, его характеристический вектор состоит из единственной компоненты, равной 3.

Поставим в соответствие каждому выпуклому многоугольнику несколько графов, которые будем называть сопутствующими графами этого многоугольника. Вершинами первого графа (назовем его структурным графом или структурой исходного многоугольника) будут вершины и точки пересечения диагоналей исходного многоугольника, а ребрам соответствуют стороны исходного многоугольника и отрезки, на которые разбиваются диагонали многоугольника точками пересечения.

Ясно, что структурный граф многоугольника является планарным. Более того, исходный многоугольник (с диагоналями) представляет собой одну из возможных плоских укладок структурного графа. Эта плоская укладка (как и каждая) порождает граф геометрически двойственный структурному. Кроме геометрически двойственных графов в теории графов рассматривают еще и абстрактно двойственные графы (см., напр., [1]). Поскольку в нашей работе абстрактно двойственные графы не затрагиваются, договоримся для краткости называть граф, геометрически двойственный структурному графу, двойственным или дуальным графом исходного многоугольника. Вершинами дуального графа будут грани плоской укладки структурного графа, т.е. элементарные многоугольники плюс внешняя n-угольная грань. Две вершины дуального графа смежны, если соответствующие грани имеют общее граничное ребро. В общем случае геометрически двойственный граф не является классическим. Он может содержать петли и кратные ребра. Поскольку петли соответствуют мостам исходного графа, в нашем случае у двойственного графа петель не будет. Кратные ребра в геометрически двойственном графе возникают тогда и только тогда, когда две разные грани могут иметь более одного общего ребра. Применительно к нашему случаю это означает, что дуальный граф будет иметь кратные ребра тогда и только тогда, когда исходный многоугольник является треугольником.

В некоторых случаях вместо дуального графа удобнее использовать граф, который получается удалением у дуального графа вершины, соответствующей внешней грани структурного графа. Такой граф будем называть внутренним графом многоугольника. Внутренний граф любого выпуклого многоугольника является классическим. В частности, внутренний граф треугольника будет одновершинным. Еще одним важным свойством внутреннего графа является его двудольность, в то время как дуальный граф двудолен тогда и только тогда, когда n нечетно.

Рис. 2.1                                                   Рис. 2.2

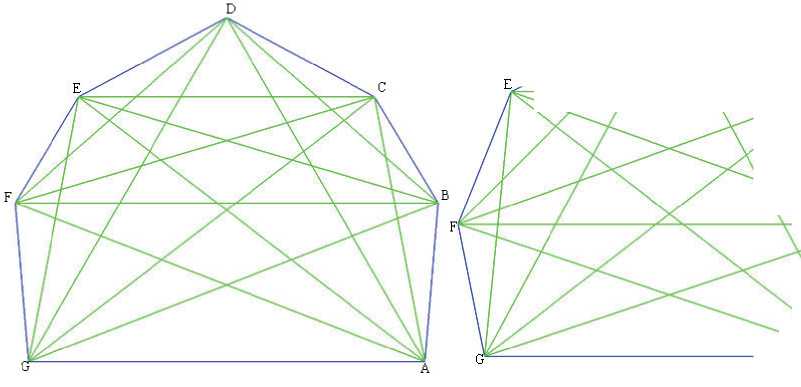
На рис. 2.1 и 2.2 представлены соответственно дуальный и внутренний графы семиугольника, изображенного на рис. 1. Вершины дуального и внутреннего графов пронумерованы в полном соответствии с нумерацией элементарных многоугольников на рис. 1. Зеленым цветом выделены вершины, соответствующие граням, смежным внешней, т.е. элементарным треугольникам, одна из сторон которых является стороной исходного семиугольника. Красным цветом на рис. 2 выделена вершина, соответствующая внешней грани.

Каждый из графов, сопоставленных любому выпуклому многоугольнику, очевидно планарен и связен. В то же время другие важные характеристики сопутствующих графов могут варьироваться. Именно на этой вариативности и основаны предлагаемые нами подходы к классификации выпуклых многоугольников. Из многочисленных возможных характеристик графов предпочтение мы отдавали наиболее существенным, имеющим наглядную геометрическую интерпретацию и естественно описы- ваемым в терминах исходного многоугольника.

Важнейшими характеристиками каждого графа являются число его вершин и количество ребер. Поскольку дуальный граф по определению имеет столько же ребер, сколько и структурный, для классификации графов по количеству ребер достаточно рассматривать графы лишь одного определенного вида, например, структурные.

Число вершин структурного графа ординарного многоугольника зависит только от n и подсчитывается по формуле v0(n) = n + C4 = n(n +1)(n2 - 7n +18)/24. Легко доказать индукцией по k, что каждая особенность порядка k уменьшает количество вершин структурного графа на k(k + 3)/2. Поэтому число вершин структурного графа многоугольника с характеристическим вектором χ вычисляется по формуле:

1 m

1 m

v ( n , x ) = v o ( n ) - ^ Д s k k ( k + 3) (1)

Число D =  Z s ,k(k + 3) назовем дефектом пересечений исходного многоугольника. Выпук- v 2 k=i k лые n-угольники, структурные графы которых имеют поровну вершин (а значит и точек пересечения диагоналей), будем называть равнопересеченными.

Число ребер структурного (а значит, и дуального) графа ординарного n-угольника подсчитывается тривиально: e₀(n ) = 2 C + n ( n - 3)/2 + n = n ( n - 1)( n - 5 n + 12)/12 . Для обоснования этой формулы достаточно учесть, чт ⁿ о у выпуклого n-угольника n(n – 3)/n диагоналей; число ребер на каждой диагонали на единицу больше, чем число точек пересечения диагоналей, инцидентных данной диагонали; каждая точка пересечения диагоналей инцидентна четырем ребрам; каждое ребро инцидентно двум вершинам; наряду с частями диагоналей, стороны исходного многоугольника также являются ребрами структурного графа. Особая точка порядка k уменьшает число ребер на k(k + 2). Поэтому формула для количества ребер структурного (дуального) графа выпуклого многоугольника с характеристическим вектором χ выглядит так:                  _m

e ( n , X ) = e ₀ ( n ) — 2 s_kk ( k + 2) ⁽²⁾

k = 1

Число Dp = Z s, k(k + 2) назовем дефектом ребер исходного многоугольника. Выпуклые k=1 k n-угольники, структурные (дуальные) графы которых имеют поровну ребер, будем называть равнореберными.

Формула для подсчета числа вершин внутреннего графа ординарного n-угольника получается применением соотношения Эйлера (см. напр., [1]) для плоской укладки планарного графа: f o ( n ) = 1 + e о ( n ) - v о ( n ) = ( n - 1)( n - 2)( n² - 3 n + 12)/24 . Наличие полюса k-го порядка уменьшает количество вершин внутреннего (дуального) графа на k(k + 1)/2. Поэтому для n-угольника с характеристическим вектором χ формула для числа вершин внутреннего графа следующая:

• 1    m

f ( n, x ) = f > ( n ) ^- - 2 s k k ( k + 1) (3)

• ^{2    k} =1                               1 m

Разумеется, у дуального графа будет f ( n , х ) = f ) ( n ) + 1 вершин. Число Dr = Z S k^k ( k + 1) на-

^J 2 k = 1

зовем дефектом граней исходного многоугольника. Ясно, что Dv + Df = De . Выпуклые n-угольники, внутренние (дуальные) графы которых имеют поровну вершин (а структурные – поровну граней в плоской укладке), будем называть равногранными. Наконец, выпуклые n-угольники, у которых совпадают любые две (а значит, в силу соотношения Эйлера, и все три) рассмотренные выше характеристики, назовем изопараметрическими. Очевидно, что каждое из описанных нами отношений (равнопересечен-ность, равнореберность, равногранность и изопараметричность) является отношением эквивалентнос- ти на множестве выпуклых n-угольников.

Перейдем к классификации многоугольников по степеням вершин сопутствующих графов. В первую очередь отметим, что мультимножество степеней вершин структурного графа выпуклого многоугольника вполне определено его характеристическим вектором. В самом деле, степень каждой из вершин структурного графа, соответствующих вершинам исходного многоугольника, равна n – 1. Степень каждой из остальных вершин равна 4 при условии, что эта вершина не является полюсом. Количество таких вершин определяется дефектом пересечений, который, в свою очередь, однозначно определен характеристическим вектором. Два выпуклых n-угольника назовем изополярными , если их характеристические векторы равны.

Известно, что максимальное число сторон элементарного многоугольника, который может (но не обязан) получиться в разбиении выпуклого n-угольника равно n, когда n нечетно, и n – 1, когда n – четно [2]. Вектором граней выпуклого n-угольника назовем упорядоченный набор ф = ( ф ₃ , ф ₄ ,... , ф _п ), такой, что ϕ _k равно количеству элементарных k-угольников в разбиении исходного многоугольника. По вектору граней однозначно восстанавливаются мультимножества степеней вершин дуального и внутреннего графов. Два выпуклых n-угольника назовем однотипными , если их векторы граней равны.

Изополярность и однотипность, конечно, тоже являются отношениями эквивалентности и следовательно, пригодны для классификации выпуклых n-угольников.

Наиболее детальную классификацию выпуклых многоугольников в терминах сопутствующих графов можно получить, положив в основу классификации изоморфизм этих графов. Известно, что геометрически двойственные графы изоморфных связных планарных графов могут не быть изоморфными [1]. Однако в интересующем нас случае такая ситуация невозможна: изоморфизм структурных графов влечет за собой изоморфизм дуальных (и наоборот). При n = 3 этот факт проверяется непосредственно. При остальных n структурные и дуальные графы трехсвязны. Для трехсвязных планарных графов плоская укладка определена однозначно с точностью до изоморфизма геометрически двойственных графов [3].

Два выпуклых многоугольника будем называть изотопными, если изоморфны их структурные (дуальные) графы. Введение такого термина оправдано еще и тем, что два многоугольника будут изотопны в смысле введенного нами определения тогда и только когда, когда они будут изотопны в R2 в топологическом понимании этого термина.

Из предыдущих рассуждений ясно, что группы автоморфизмов структурного и дуального графов (при n>3) изоморфны. Порядок этой общей группы автоморфизмов может служить определенной мерой симметрии исходного многоугольника.

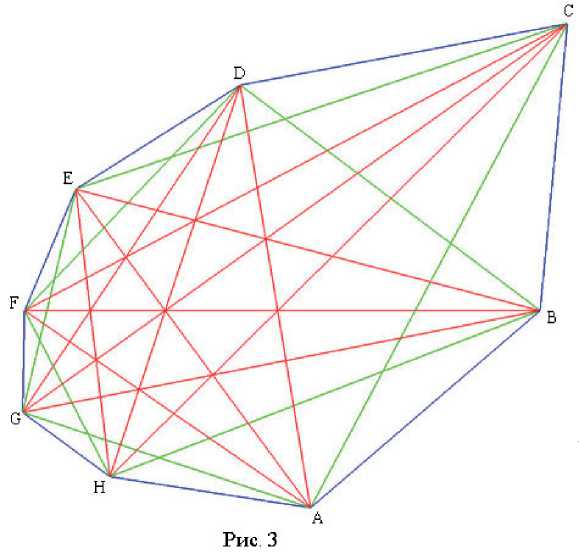
Конечно, понимаемая таким образом симметрия не является симметрией в геометрическом смысле. Так, у восьмиугольника, изображенного на рис. 3 группа самосовмещений (т.е. группа движений плоскости, отображающих данный восьмиугольник на себя) тривиальна, в то время как группа автоморфизмов сопутствующего графа является группой диэдра восьмой степени и состоит из 16 элементов. Это не удивительно, если учесть, что в классе восьмиугольников, изотопных данному, имеется правильный восьмиугольник, группа самосовмещений которого изоморфна группе диэдра восьмой степени.

Описанная ситуация вполне типична. Как правило, группа автоморфизмов сопутствующего графа выпуклого n-угольника является подгруппой группы диэдра n-ой степени, и среди многоугольников, изотопных данному, имеется многоугольник, группа самосовмещений которого изоморфна этой подгруппе. Единственное исключение из этого правила имеется при n = 5. Группа автоморфизмов структурного графа выпуклого пятиугольника (не важно, какого именно, т.к. все они изотопны) содержит 20 элементов, т.е. вдвое больше, чем соответствующая группа диэдра. Это связано с тем, что структурный граф выпуклого пятиугольника допускает автоморфизмы, при которых вершины графа, соответствующие вершинам исходного многоугольника, меняются местами с вершинами, соответствующими точкам пересечения диагоналей

исходного многоугольника. В то же время каждый автоморфизм структурного графа любого другого многоугольника отображает множество вершин исходного многоугольника на себя.

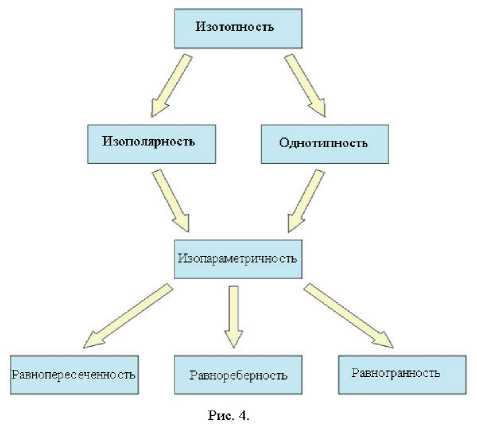
Рассмотренные нами классификации выпуклых многоугольников не являются независимыми. Поскольку любые характеристики изоморфных графов одинаковы, изотопные многоугольники одновременно представляют собой и изополярные, и однотипные, и изопараметрические и т.д. Мультимножество степеней вершин графа однозначно определяет количество его вершин и ребер, поэтому изополярные графы обязательно изопарамет-ричны. Точно также изопараметричность графов вытекает из их однотипности. Совершенно очевидно также, что из изопараметричности многоугольников вытекает их равнопересеченность, равнореберность и равногранность. В результате получается логическая зависимость классификаций (рис. 4).

Покажем, что между рассматриваемыми классификациями нет других попарных зависимостей. Заметим, что отсутствие попарных зависимостей не означает, что наши классификации независимы в совокупности. Например, как уже отмечалось, любые два из отношений равнопересе-ченности, равнореберности и равногранности влекут за собой третье.

Многоугольники, используемые в приведенных ниже примерах, построены с помощью специальной программы, разработанной авторами в системе компьютерной алгебры Maple 12. Эта программа по координатам вершин исходного многоугольника проверяет его на выпуклость, строит сам многоугольник и его сопутствующие графы, находит характеристический вектор и вектор граней. Красным цветом на рисунках, построенных с помощью этой программы, выделены диагонали, участвующие в формировании полюсов.

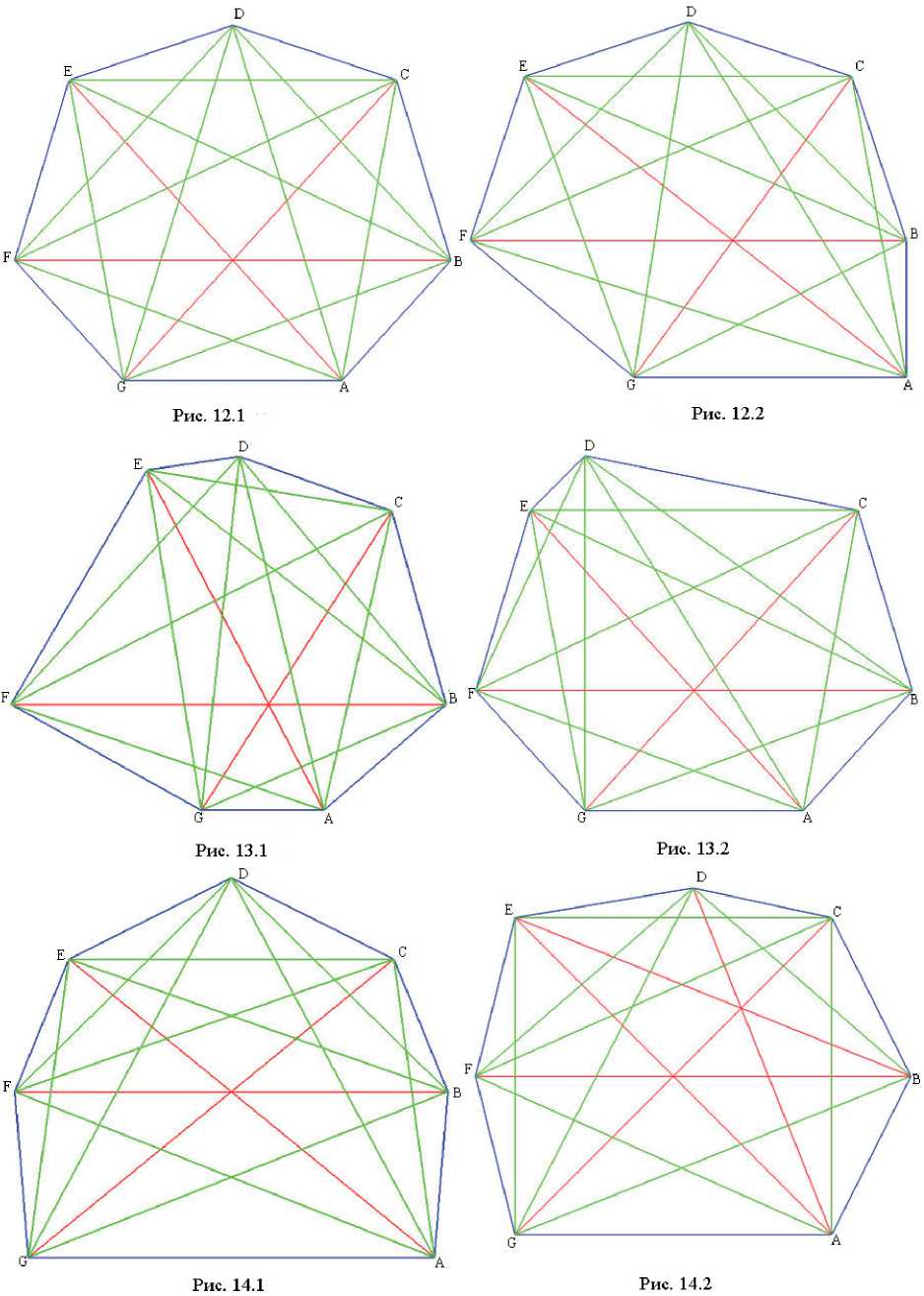
Семиугольники, изображенные на рис. 11.1 и 11.2, однотипны и изополярны, но не изотопны. А семиугольники на рис. 12.1 и 12.2 изополярны, но не однотипны. Характеристические векторы восьмиугольни-

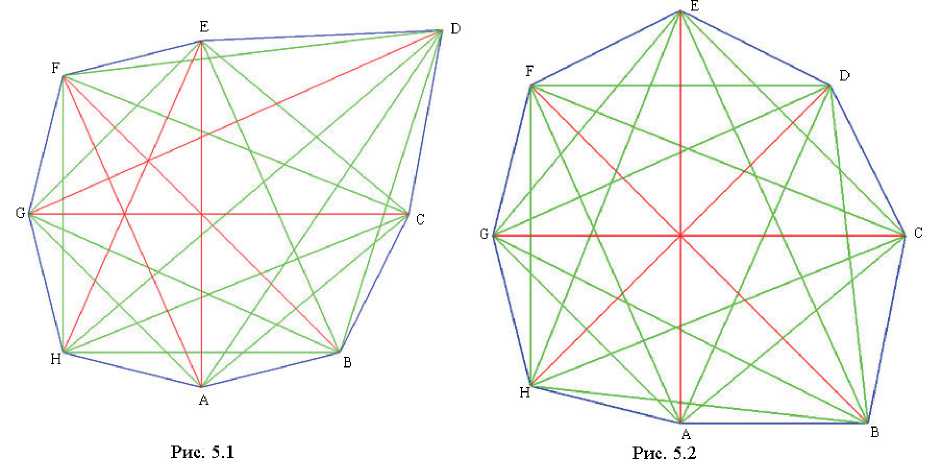
ков, изображенных на рисунках 5.1 и 5.2, соответственно (3, 0) и (0, 1). Следовательно, на основании формул (1), (2) и (3), они равногранны, но при этом не являются, ни равнореберными, ни равнопересеченными.

Для построения других примеров, разделяющих три наиболее слабых отношения на нашей схеме, потребуются многоугольники, имеющие несколько полюсов второго порядка. Поэтому они должны иметь не менее девяти сторон.

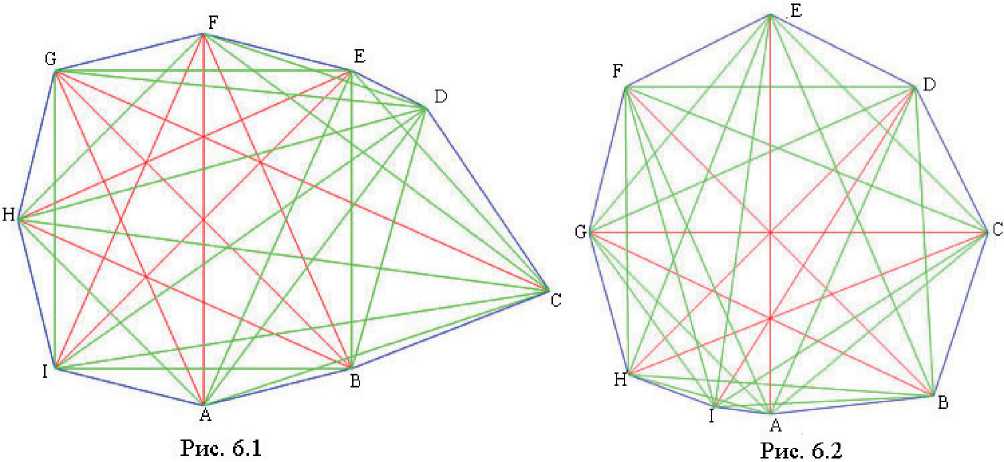
Девятиугольники, изображенные на рис. 6.1 и 6.2, имеют характеристические векторы (5, 0) и (0, 2) соответственно. В связи с этим на основании формул (1), (2) и (3) данные девятиугольники являются равнопересеченными, но не являются ни равнореберными, ни равногранными.

Равнореберные, но не равнопересеченые и не равногранные девятиугольники представлены на рис. 7.1 и 7.2. В этом легко убедиться, учитывая, что у первого из них 8 полюсов первого порядка, а у второго – 3 полюса второго порядка.

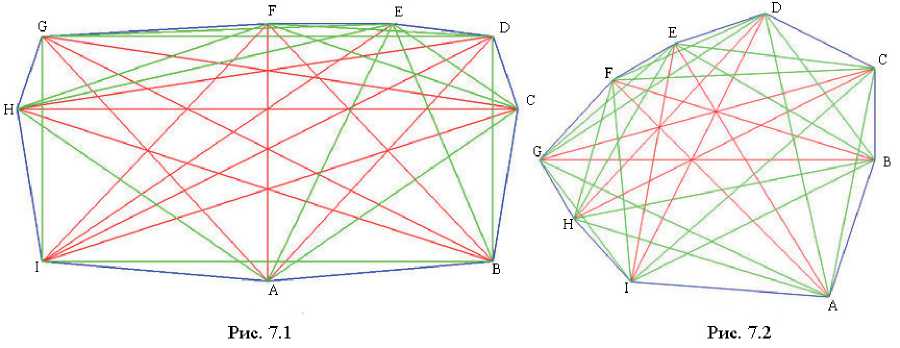
Наиболее сложно построить пример однотипных (а значит, изопараметрических), но не изополярных многоугольников. Опишем, как можно их построить. Во-первых, найдем различные характеристические векторы, приводящие к одинаковым дефектам вершин и граней (и ребер). В качестве таковых можно взять, например, векторы (3, 0, 1) и (0, 3, 0). Десятиугольник с характеристическим вектором (3, 0, 1) можно построить из восьмиугольника c характеристическим вектором (3, 1). Для этого одну из недостающих вершин добавим произвольно, а другую так, чтобы прямая, соединяющая добавляемые вершины, проходила через полюс второ- го порядка. Десятиугольник с характеристическим вектором (0, 3, 0) можно получить из девятиугольника, изображенного на рис. 7.2. В обоих случаях вершины добавляются так, чтобы полученные многоугольники были выпуклыми и не содержали «лишних» особых точек. Разумеется, полученные десятиугольники будут изопараметрическими, но не обязательно однотипными. Однако, используя определенную произвольность в выборе девятой и десятой вершин десятиугольника с характеристическим вектором (3, 0, 1) и десятой вершины десятиугольника с характеристическим вектором (0, 3, 0), мы получили несколько пар не изо-полярных, но однотипных десятиугольников. Одна такая пара представлена на рис. 8.1 и 8.2.

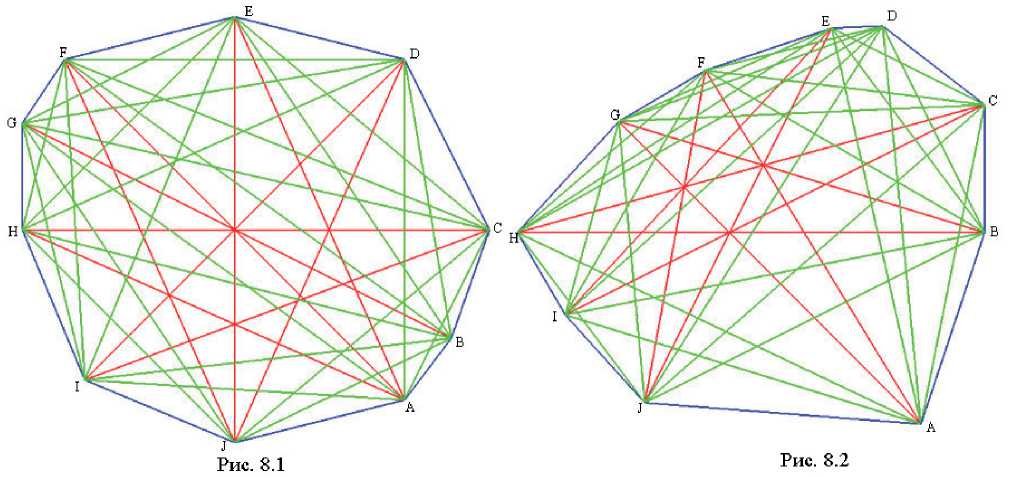
Каждый из многоугольников, изображенных на рис. 8.1 и 8.2, разбивается своими диагоналями на 120 треугольников, 80 четырехугольников, 31 пятиугольник, 5 шестиугольников и один семиугольник. Конечно, разглядеть все элементарные многоугольники затруднительно из-за недостаточного масштаба рисунков. Поэтому приведем координаты вершин десятиугольников: десятиугольник на рис. 8.1: A (80; -80), B (102; -51), C (120; 0), D (80; 80), E (0; 100), F (-80; 80), G (-100; 50), H (-100; 0), I (-1200/17; -1200/17), J (0; -100); десятиугольник на рис. 8.2: A (90; -90), B (120; 0), C (120; 60), D (72; 97), E (48; 96), F (-2750/241; 18350/241), G (-1200/23; 1200/23), H (-100; 0), I (-2400/31; -1200/31), J (-40; -80).

Каждая из рассмотренных нами классификаций приводит к разбиению выпуклых n-угольников на конечное число классов при каждом конкретном значении n. При n ≤ 5 все классификации тривиальны. При n = 6 картина тоже достаточно прозрачна. Выпуклые шестиугольники разбиваются на два класса независимо от того, какую именно классификацию мы рассматриваем. Один класс составляют ординарные шестиугольники, а другой – особенные.

Первый содержательный случай возникает при n = 7. Опишем все классы изотопных выпуклых семиугольников. Начнем с рассмотрения семиугольника, изотопного правильному (рис. 9). Рассмотрим элементарные треугольники (на рис. 9 они пронумерованы), примыкающие к единственно-

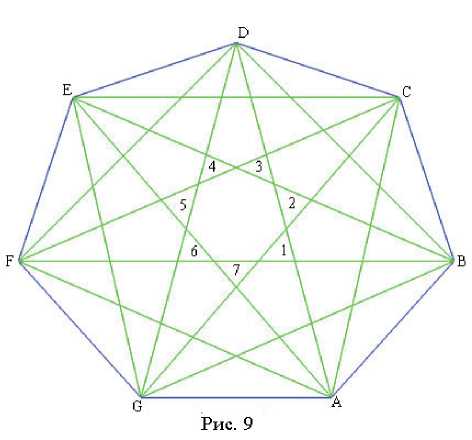
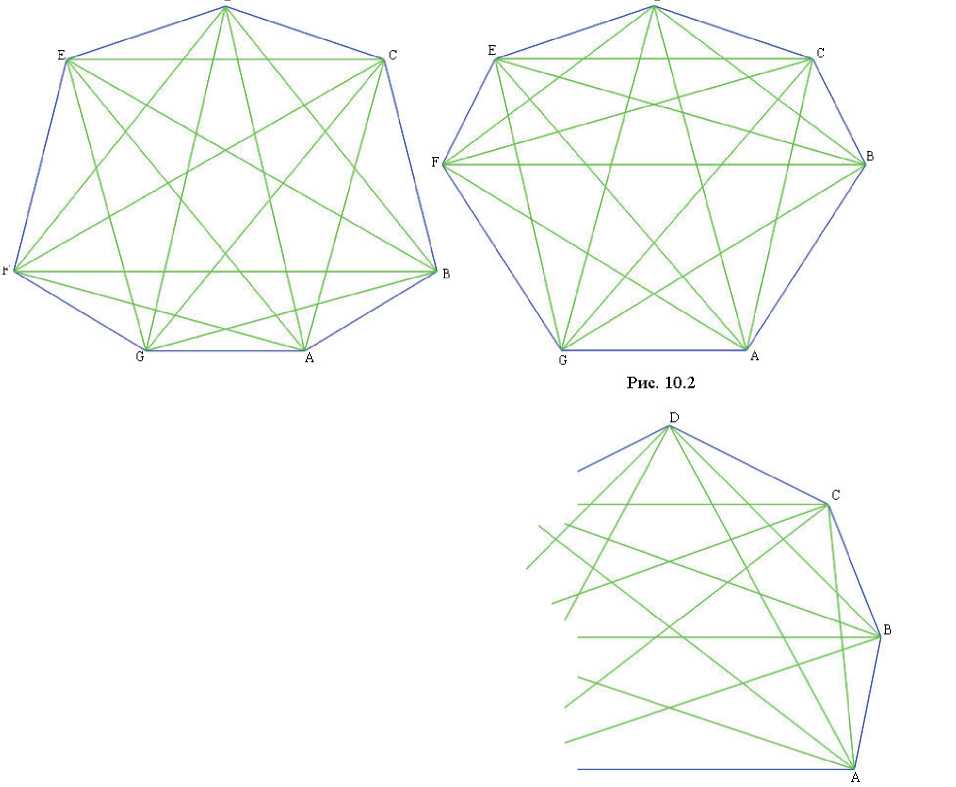
му элементарному семиугольнику. Вариативность выпуклых семиугольников обеспечивается тем, что каждый из пронумерованных элементарных многоугольников может выродиться в точку или инвертироваться . Например, перемещая вершины B и F можно получить из многоугольника, изображенного на рис. 9, многоугольник на рис. 12.1, в котором исчез (выродился в особую точку) треугольник № 7. Продолжая перемещать вершины B и F можно получить семиугольник, изображенный на рис. 10.1, в котором треугольник № 7 будет инвертирован, т.е. точка пересечения диагоналей AE и CG окажется по другую сторону от диагонали BF. При этом у соседних пронумерованных элементарных многоугольников изменится число сторон.

Базовым циклом выпуклого семиугольника назовем упорядоченный набор вида [a₁, a₂, …, a₇], где a i е { - 1, 0,1}. Причем a i = - 1, если i -й пронумерованный элементарный многоугольник инвертирован, и а_i= 0, если соответствующий элементарный многоугольник выродится в особую точку. Так, семиугольник, изображенный на рис. 9, имеет базовый цикл [1,1,1,1,1,1,1], а семиугольник на рис. 10.1 – [1,1,1,1,1,1, – 1]. Будем считать два базовых цикла эквивалентными, если каждый из них получается из другого циклическим сдвигом и, возможно, изменением направления обхода. Очевидно, что справедливы следующие утверждения:

• •    каждый ноль в базовом цикле окружен единицами;

• •    каждая минус единица также окружена единицами;

• •    каждому классу эквивалентных базовых циклов, обладающих свойствами, отмеченными в предыдущих пунктах, соответствует ровно один класс изотопных выпуклых семиугольников;

• •    наоборот, каждому классу изотопных выпуклых семиугольников соответствует свой класс эквивалентных базовых циклов, обладающих свойствами, указанными в первых двух пунктах.

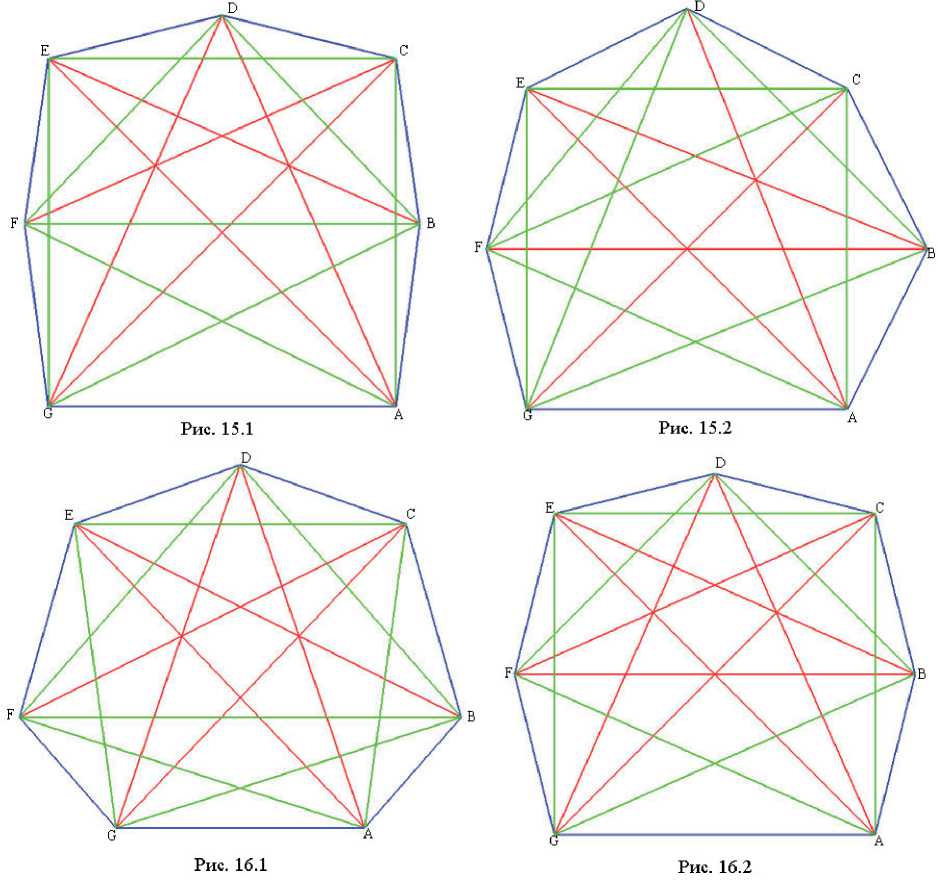
Таким образом, подсчет количества классов изотопных выпуклых семиугольников сводится к подсчету числа классов эквивалентных базовых циклов. Последнее можно подсчитать, используя теорию перечисления Пойа. Однако в нашем случае проще получить ответ прямым перебором. В табл. 1 представлены с точностью до эквивалентности все базовые циклы, а на рисунках 9 – 16.2 – соответствующие семиугольники. Характеристический вектор семиугольника состоит всего из одной компоненты, значение которой совпадает с дефектом граней этого семиугольника. Поэтому мы не стали включать в таблицу информацию о характеристическом векторе.

Таблица 1

S Он £	>5 О и	m о § с О 5 с rv Л О ё ^§ сЗ	o’ >в ffl &	3 л m	л ю S	>s	Дефект
							>5 К Он с	ю OL,	>s
9	[1,1,1,1,1,1,1]	14	(35,7,7,0,1)	42	91	50	0	0	0
10.1	[1,1,1,1,1,1,-1]	2	(33,10,6,1,0)	42	91	50	0	0	0
10.2	[-1,1,1,1,1,-1,1]	2	(32,11,7,0,0)	42	91	50	0	0	0
11.1	[1,-1,1,1,-1,1,1]	2	(31,13,6,0,0)	42	91	50	0	0	0
11.2	[1,-1,1,1,-1,1,-1]	2	(31,13,6,0,0)	42	91	50	0	0	0
12.1	[1,1,1,1,1,1,0]	2	(34,9,5,1,0)	40	88	49	2	3	1
12.2	[1,-1,1,1,1,1,0]	1	(32,12,5,0,0)	40	88	49	2	3	1
13.1	[1,1,-1,1,1,1,0]	1	(32,12,5,0,0)	40	88	49	2	3	1
13.2	[1,1,-1,1,-1,1,0]	1	(31,14,4,0,0)	40	88	49	2	3	1
14.1	[1,-1,1,1,-1,1,0]	2	(30,16,3,0,0)	40	88	49	2	3	1
14.2	[1,0,1,1,1,1,0]	2	(33,11,4,0,0)	38	85	48	4	6	2
15.1	[1,0,1,1,0,1,1]	2	(33,11,4,0,0)	38	85	48	4	6	2

Окончание таблицы 1

s Ph £	>s S н о 8 § И	m о § с О 5 G CL о E   § G о cd	o’ >B	л m	Ю G	aS cd	Дефект
							)S S И я с	ю G	s s cd &
15.2	[1,0,1,1,-1,1,0]	1	(31,15,2,0,0)	38	85	48	4	6	2
16.1	[1,0,1,1,0,1,-1]	2	(31,15,2,0,0)	38	85	48	4	6	2
16.2	[1,0,1,1,0,1,0]	2	(32,14,1,0,0)	36	82	47	6	9	3

Из таблицы видно, что выпуклые семиугольники разбиваются на 15 классов изотопных и на 11 классов однотипных семиугольников. В силу того, что у семиугольника не может быть полюсов, порядок которых выше первого, характеристический вектор, дефекты пересечений, ребер и граней полностью определены только количеством полюсов. Поскольку их может быть не более трех, остальные рассмотренные нами классификации приводят к одному и тому же разбиению выпуклых семиугольников на 4 класса.

f^L_—\—/—/\ —\—/—"e^^1 G                  A Рис. 10.1 D J^ Рис. 11.1

G                      A Рис. 10.2 D /                                        \в Ct                                                            a Рис. 11.2

Полное описание всех классов изотопных выпуклых восьмиугольников представляется весьма сложной задачей. Аналогичная ситуация и с однотипными выпуклыми восьмиугольниками. Грубые оценки показывают, что число классов в этих случаях измеряется тысячами. Гораздо медленнее с ростом числа сторон исходного многоугольника растет количество возможных характеристических векторов, а значит, и количество классов многоугольников при тех классификациях (см. рис. 4.), в которых каждый класс однозначно определен характеристическим вектором.

Нами построены восьмиугольники с характеристическими векторами [4]: (0, 0); (1, 0); (2, 0); (3, 0); (4, 0); (5, 0); (6, 0); (7, 0); (8, 0), (9, 0), (0, 1); (1, 1); (2, 1); (3, 1); (4, 1); (6, 1); (8, 1). По-видимому, выпуклых восьмиугольников, имеющих характеристические векторы, отличные от приведенных, не существует. Те же самые классы возникают, если вместо отношения изополярности рассматривать отношение равнопересеченности, равнореберности или изопараметричности. Если же в основу классификации положить отношение равногранности, то выпуклые восьмиугольники разобьются на 10 классов.

В табл. 2 для каждой из рассмотренных нами классификаций приведены числа классов, на которые разбиваются выпуклые n-угольники для небольших значений n. Исключениями являются числа классов изотопных и однотипных восьмиугольников.

Таблица 2

Число сторон	Число классов
	изотопных	однотипных	изополярных	изопараметри-ческих	равнопересеченных	равнореберных	равногранных
	выпуклых многоугольников
3	1	1	1	1	1	1	1
4	1	1	1	1	1	1	1
5	1	1	1	1	1	1	1
6	2	2	2	2	2	2	2
7	15	11	4	4	4	4	4
8	?	?	17	17	17	17	10

При малых n рассматриваемые нами отношения нередко приводят к совпадающим разбиениям. В то же время, начиная с n = 9, любые два из введенных отношений приводят к различным разбиениям. Задача отыскания точного числа классов выпуклых n-угольников с ростом n становится весьма сложной для каждой из рассматриваемых классификаций. Подтверждением этого тезиса может служить тот факт, что даже для правильных n-угольников полное описание характеристического вектора с произвольным n было получено относительно недавно [5].

Разумеется, классификации на основе отношений изотопности, однотипности, изополярности, изопраметричности, равнопересеченности, равнореберности и равногранности не исчерпывают возможных подходов к классификации выпуклых n-угольников с помощью сопутствующих графов. Рассмотрение других (не затронутых нами ранее) характеристик сопутствующих графов тоже может (хотя и не обязательно) приводить к содержательной классификации выпуклых многоугольников.

Так, диаметр внутреннего графа выпуклого n-угольника зависит только от n и равен (n2 – 8)/4 при четных n и (n2 – 9)/4 – при нечетных. В связи с этим диаметр внутреннего графа n-угольника не может служить основой для содержательной классификации. В то же время радиус внутреннего графа выпуклого n-угольника зависит от вида многоугольника. Например, при n = 21 радиус внутреннего графа может меняться в диапазоне от 54 до 60 [4]. Таким образом, радиус внутреннего графа годится в качестве основания для классификации. Переменной величиной (в том числе и при фиксированном радиусе) является количество центральных вершин внутреннего графа выпуклого n-угольника. Это дает нам еще одну возможную классификацию.