Кластер-анализ пульсовой волны человека самоорганизующимися картами Кохонена для выявления маркеров возрастных групп

Настоящее исследование носит методологический характер и описывает подход к изучению сердечно-сосудистой системы человека. Оценка биологического возраста важна для управления процессом старения человека. Регулярный мониторинг этого показателя позволяет принимать профилактические меры по снижению вероятности сердечно-сосудистых катастроф. Целью исследования является определение возрастных групп по пульсовым волнам испытуемых с применением нейронных сетей Кохонена. В этом исследовании самоорганизующиеся карты Кохонена применялись для кластеризации пульсовых волн людей различного возраста путём наблюдения за динамическим изменением пульсовой волны с подбором параметров алгоритма самоорганизации нейронной сети. Использовался набор данных различных возрастных групп. Каждая группа содержала файлы испытуемых одного и того же возраста, каждый файл – пульсовые волны этих испытуемых. В результате экспериментов с конфигурациями нейронных сетей были получены кластерные структуры и установлены геометрические характеристики пульсовых волн, соответствующие возрастным группам. Использовавшийся алгоритм кластеризации разбил пульсовые волны на кластеры, достоверность которых в ряде случаев достигла 91 – 96 %. Программная реализация обученной нейронной сети и портативность прибора для измерения пульсовой волны позволяют применять предложенную методику для мониторинга состояния сердечно-сосудистой системы у людей, подверженных риску сердечно-сосудистых катастроф, а также людей, связанных с опасными профессиями, спортсменов, офисных работников и др. Регистрация изменений биологического возраста способствует принятию своевременных решений по модификации питания, образа жизни и физической активности. Полученная сеть может быть использована в диагностических системах поддержки принятия медицинских решений.

но применяются в медицине для клинической диагно-

Искусственные нейронные сети (ИНС) обладают значительным преимуществом при решении задач, которые либо не имеют алгоритмического решения, либо решение является сложным. Эти сети эффектив- стики, анализа изображений и сигналов, а также для интерпретации этих сигналов. В частности, для предупреждения сердечной катастрофы используются нейронные сети, выполняющие задачи классификации. Таким образом, нейронная сеть является одним из

ID 0000-0003-3176-5279

0000-0003-1747-9014

ID 0000-0002-1648-6135

0009-0008-4716-4252

Эта статья доступна в соответствии с условиями лицензии Creative Commons Attribution-NonCommercial 4.0 International

License (CC BY-NC 4.0)

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License (CC BY-NC 4.0)

Рис. 1. Образец пульсовой волны: по OX – время (мс); по OY – давление (мм рт. ст.)

наиболее часто используемых методов классификации биений в ЭКГ.

Важным преимуществом нейросетевой кластеризации (в отличие от традиционных нейронных сетей, обучаемых с учителем) является то, что самоорганизующимися нейронными картами Кохонена можно визуализировать кластеры и в наглядной форме определить их различия или характерные маркеры, ответственные за те или иные классы эквивалентности. В данном в случае такими классами эквивалентности являются возрастные группы. Такого эффекта невозможно достичь, используя традиционные нейронные сети, которые, хоть и дают лучшую точность распознавания, но не основаны исключительно на геометрии, так как обучаются с учителем методом подстройки весовых коэффициентов под заранее известный результат.

Обзор по теме исследования

В исследовании [1] авторы ставили задачу определить, можно ли диагностировать и контролировать диабет второго типа и его осложнения, включая гипертонию и гиперлипидемию, с помощью пульсовой волны (ПВ). Различные модели машинного обучения, такие как линейный дискриминантный анализ, машины опорных векторов (SVM) и случайные леса, применялись для классификации контрольной группы, пациентов с диабетом и пациентов с диабетом с осложнениями. В работе [2] создан автоматический метод, основанный на контролируемых методах обучения, способный отличать здоровую артериальную пульсовую волну от патологической. Проведено сравнительное исследование для оценки производительности двух классификаторов: машины опорных векторов (SVM) и искусственной нейронной сети (ИНН). SVM достигла статистически значимого повышения производительности для этой задачи. В статьях [3; 4] исследовали, может ли форма пульсовой волны, воспроизведённая по неинвазивным измерениям диаметра и скорости артерий, обнаруживать нарушения в работе сердца человека. В результате применения машинного обучения к метрикам выявлено, что классификатор опорных векторов (SVM) может одновременно обеспечивать до 99 % полноты и 95 % точности распознавания. В работах [5; 6] рассмотрен подход к непрерывному измерению артериального давления (АД), основанный на времени прохождения импульса (ВПИ) между двумя точками кровеносного сосуда и форме пульсовой волны (ПВ). Использование машинного обучения позволило снизить погрешность измерения артериального давления. В исследовании [7] представлено применение методов машинного обучения для выявления стенозов и аневризм в артериальной системе человека с помощью измерения скорости потока крови. Выявлено, что применение методов Random Forest и Gradient Boosting позволяет получать достоверные результаты. В статьях [8; 9] представлено фотоплетизмографиче-ское (ФПГ) устройство для измерения времени прохождения импульса и скорости пульсовой волны с использованием датчиков. С помощью нейронной сети построена модель прогнозирования для ишемической болезни сердца со средней точностью 83 %. В работах [10–15] предложены неинвазивные методы измерения давления с помощью машинного обучения и анализа пульсовой волны.

В целом анализу проблематики пульсовых волн для поддержки принятия медицинских решений, в том числе для задач диагностики атеросклероза, в травматологии и ортопедии, для математического моделирования системы кровообращения, гемодинамики и биопротезирования и др., посвящено множество работ [16–40].

Материалы и методы

В данной работе использовались данные из базы пульсовых волн, которые были накоплены группой ученых ИМАШ РАН в течение продолжительного времени. ПВ были сняты с лучевой артерии на запястье руки испытуемого при помощи специализированных волоконно-оптических датчиков [41–43]. Далее эти данные были переведены в цифровой вид, а также визуализированы на экране монитора с помощью специально разработанного программного приложения (рис.1). Для эксперимента выбирались пакеты пульсовых волн различных возрастных категорий.

Самоорганизующиеся карты ( SOM ), известные также как карты Кохонена, представляют собой тип искусственных нейронных сетей, способных преобразовывать сложные нелинейные статистические взаимосвязи между элементами данных высокой размерности в простые геометрические взаимосвязи в пространстве меньшей размерности. В SOM нейроны организованы в решётку, в которой каждый нейрон подключён ко всем нейронам во входном слое.

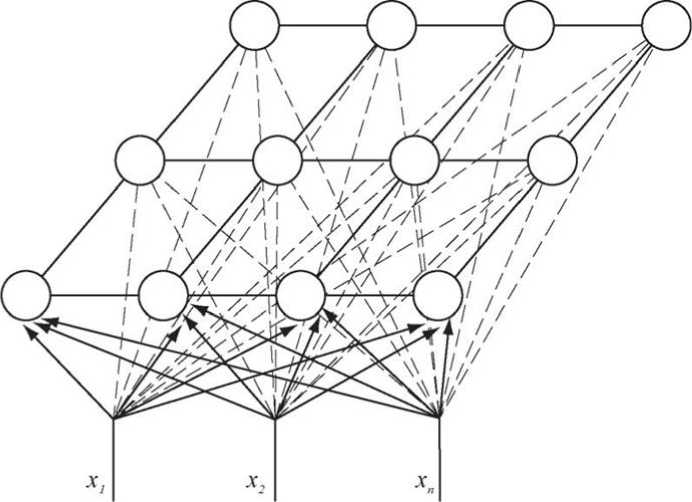
Рис. 2. Иллюстрация структуры SОМ

Иллюстрация SОМ приведена на рис. 2.

Каждый нейрон имеет связанный вектор весов. Процесс обучения включает пошаговое выполнение итераций обучения до тех пор, пока каждый элемент в наборе данных не будет подан на SOM определённое число раз. Итерация – это количество пакетов или шагов через разделённые пакеты обучающих данных, необходимое для завершения одной эпохи. Для каждой пульсовой волны x выиграет только один нейрон ( w n – вектор весов, более похожий на x ), и этот выигравший нейрон скорректирует свои весовые коэффициенты таким образом, чтобы при следующей итерации он интенсивнее реагировал на похожие пульсовые волны, формируя кластеры. При этом Евклидово расстояние между пульсовой волной x и весами победившего нейрона w n станет меньше. По мере того как различные нейроны выигрывают для разных пульсовых волн, способность распознавать конкретный паттерн будет возрастать. Алгоритм обучения можно представить следующим образом:

• 1.  Инициализация веса каждого нейрона.

• 2.  Инициализация t = 0.

• 3.    Случайным образом выбирается входная пульсовая волна x из набора данных.

• 4.    Определяется победивший нейрон i как нейрон, для которого

• 5.    Адаптация веса каждого нейрона n в соответствии с формулой Кохонена:

• 6.    t = t + 1.

• 7.    В случае, если t < t max , переход к шагу 3 ,

i = arg min x - w ( i )|.

w ( n ) = w ( n ) + a( t ) h ( i )( x - w ( n )).

где α( t ) называется скоростью обучения, а h(i) – функцией окрестности, которая имеет высокие значения для нейрона i и нейронов, близких к нейрону i на решётке (гауссова функция с центром на i является примером функции окрестности). Когда параметр t увеличивается, η уменьшается, при этом параметр h плавно сглаживает убывание функции. Таким образом, на каждом этапе обучения веса нейронов, близких к выигравшему, корректируются, чтобы иметь более сильную реакцию на текущий паттерн. В результате обучения расположение нейронов становится упорядоченным, и на решётке создаётся кластеризация входных пульсовых волн. Итак, если мы рассмотрим координаты связанного выигрышного нейрона для каждого паттерна, SOM формирует топографическую карту входных паттернов.

Функция соседства σ на итерации l имеет вид:

° ( l ) =--- T       т-^{п (} l )

1 + ¹ , где I = ^ .

I2

Коэффициент скорости обучения α на итерации l имеет вид:

a( l ) = -ar      Tn

1+L, где I =

I2

Результаты экспериментов

В этом исследовании мы использовали набор данных из разных возрастных групп. Каждая группа содержит файлы испытуемых того же возраста, в свою очередь, каждый файл содержит пульсовые волны соответствующего испытуемого. Мы использовали сети средние пульсовые волны

60000 -

Кластер 2

Кластер 1

50000 -

70 лет

80 лет

50 лет

40 лет

20 лет

40000 -

30000 -

20000 -

10000 -

пациенты

Рис. 3. Распределение возрастов испытуемых по сравнению с 2 кластерами: ОХ – порядковые номера испытуемых; OY – среднее значение ПВ

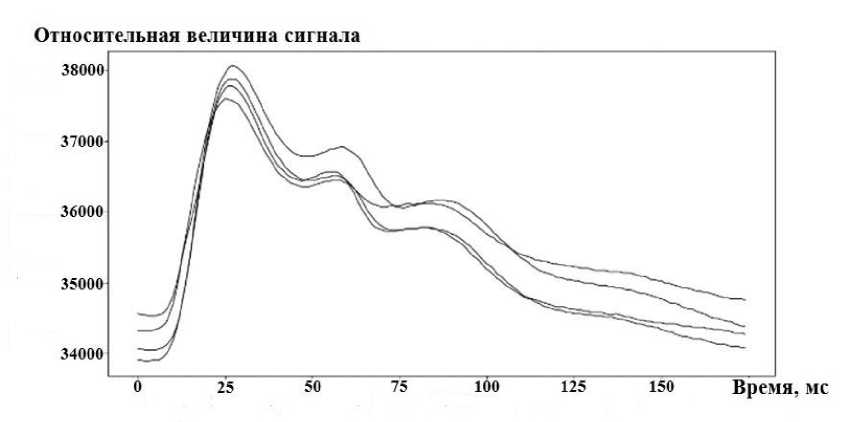
Рис. 4. Примеры пульсовых волн испытуемых из кластера 1

Кохонена, чтобы получить кластеры пульсовых волн. В результате были обнаружены кластеры, содержащие пульсовые волны испытуемых с частичным покрытием кластерами возрастных групп.

В экспериментах мы анализировали данные испытуемых разных возрастных групп (20, 40, 50 и 70 лет). Предварительно случайным образом параметры перемешали. Таким образом, SOM обрабатывает данные пульсовых волн, заранее не имея информации о возрасте. Мы использовали различные параметры SOM и входные данные, чтобы определить структуру и количество кластеров.

В начале серии экспериментов использовали SOM с решеткой 1 на 3 нейрона. Использовали гауссову функцию окрестности, начальный разброс которой σ = 1. В то же время применяли начальную скорость обучения α = 0,5. Реализованный нами алгоритм уменьшает оба параметра по мере обучения. Это позволяет быстро провести начальное обучение нейронной сети, которая затем итеративно донастраивалась в соответствии с предъявляемыми пульсовыми волнами.

Количество элементов векторов во входных данных во всех экспериментах было равно 1000 элементов. Функция, которая взвешивает окрестности позиции на карте была выбрана гауссовой. Результаты экспериментов приведены на рис. 3–16 и табл. 1–5.

На рис. 3 отображено соотношение каждой точки, которая соответствует той или иной пульсовой волне, с обозначением возраста и кластера. На рис. 4, 5 приведены примеры пульсовых волн испытуемых из кластера 1 и 2.

Таблица 1

Результаты кластеризации испытуемых в два кластера с использованием алгоритма SOM

Возраст, лет	Кластер 1, абс. / %	Кластер 2, абс. / %
20	18/19, 94	1/19, 6
40	33/34, 97	1/34, 3
50	21/22, 96	1/22, 4
70	1/15, 7	14/15, 93
80	2/23, 9	21/23, 91

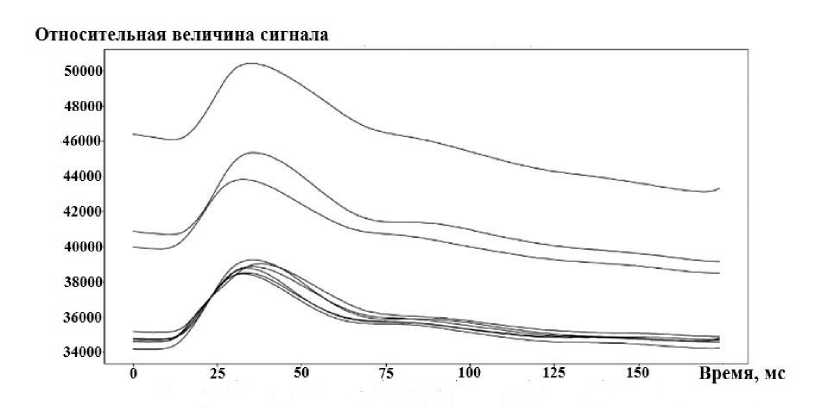
Рис. 5. Примеры пульсовых волн испытуемых из кластера 2

средние пульсовые волны

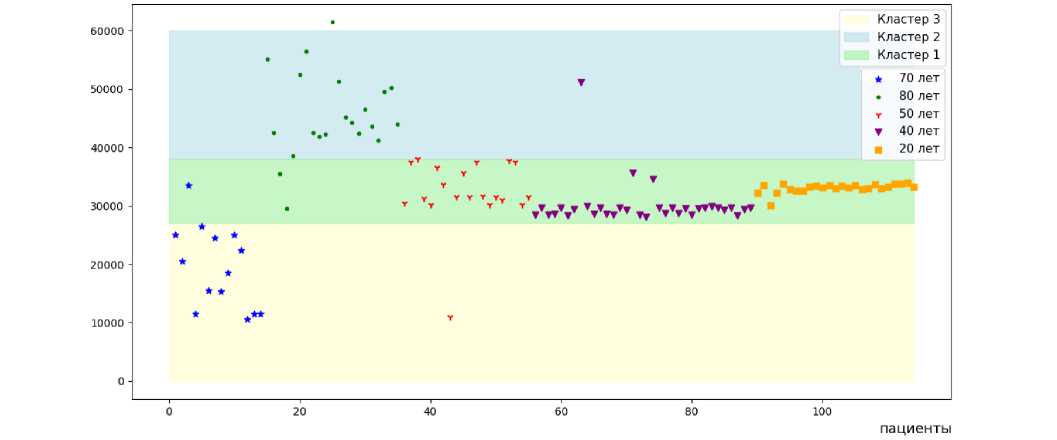
Рис. 6. Распределение возрастов испытуемых по сравнению с 3 кластерами:

OX – порядковые номера испытуемых; OY – среднее значение ПВ

В табл. 1 приведено сравнение кластеров, полученных с помощью SOM, с возрастными группами. Видно, что 94 % испытуемых 20-летнего возраста принадлежат к кластеру 1, а остальные из них (6 %) принадлежат к кластеру 2.

Было установлено, что большинство испытуемых из кластера 2 – пожилые люди. Данная кластеризация способствует выявлению людей, имеющих проблемы с сердцем.

Далее повторим те же шаги с другими параметрами алгоритма SOM , чтобы получить больше кластеров.

На рис. 6 отображено соотношение каждой пульсовой волны с обозначением возраста и кластера. На рис. 7, 8, 9 приведены примеры пульсовых волн испытуемых из кластера 1, 2 и 3. В табл. 2 приведено сравнение кластеров, полученных с помощью SOM с возрастными группами.

Получили три кластера, кластер 3 покрывает 93 % испытуемых семидесяти лет, кластер 2

Таблица 2

Результаты кластеризации испытуемых в три кластера с использованием алгоритма SOM

Возраст, лет	Кластер 1, абс. / %	Кластер 2, абс. / %	Кластер 3, абс. / %
20	18/19, 94	1/19, 6	0
40	33/34, 97	1/34, 3	0
50	21/22, 96	0	1/22, 4
70	1/15, 7	0	14/15, 93
80	2/23, 9	21/23, 91	0

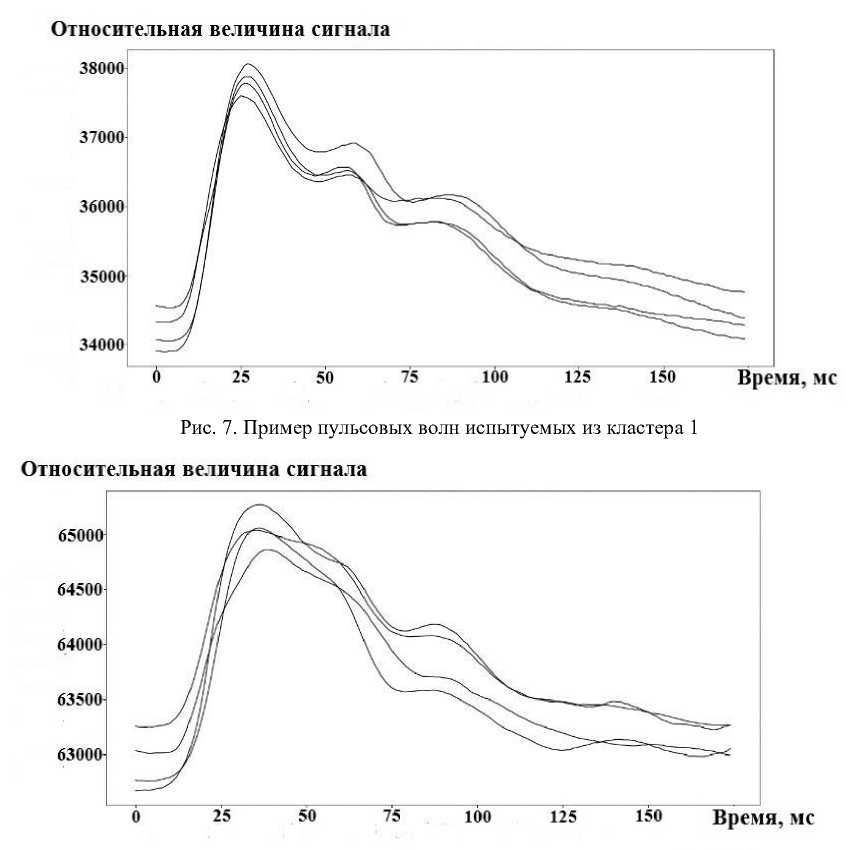
Рис. 8. Пример пульсовых волн испытуемых из кластера 2

покрывает 91 % испытуемых восьмидесяти лет и кластер 1 покрывает остальную часть испытуемых. Отметим, что на этот раз алгоритм SOM позволил получить 3 типа кластеров:

• 1.  Кластер 1 – испытуемые со средними пульсо

• 2.  Кластер 2 – испытуемые с высокими пульсо

• 3.    Кластер 3 – испытуемые с низкими пульсовыми волнами.

выми волнами.

выми волнами.

Установлено, что большинство пожилых людей входят в кластеры 2 и 3.

На рис. 10 отображено соотношение каждой точки с обозначением возраста и кластера. На рис. 11, 12, 13, 14 приведены примеры пульсовых волн испытуемых из кластера 1, 2, 3 и 4. В табл. 3 приведено сравнение кластеров, полученных с помощью SOM с возрастными группами.

На рис. 15 показано распределение возрастов испытуемых по кластерам в соответствии с характеристиками пульсовых волн.

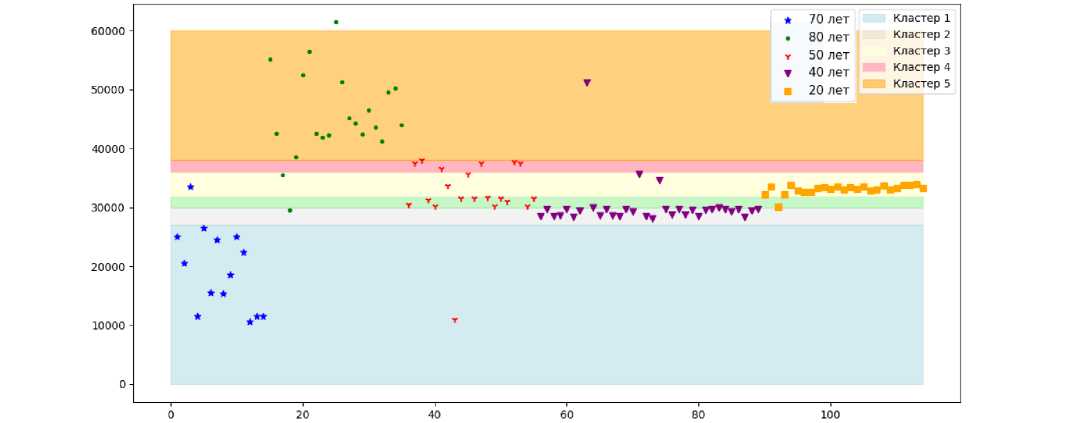
На рис. 16 отображено соотношение каждой точки, которая соответствует той или иной пульсовой волне, с обозначением возраста и кластера.

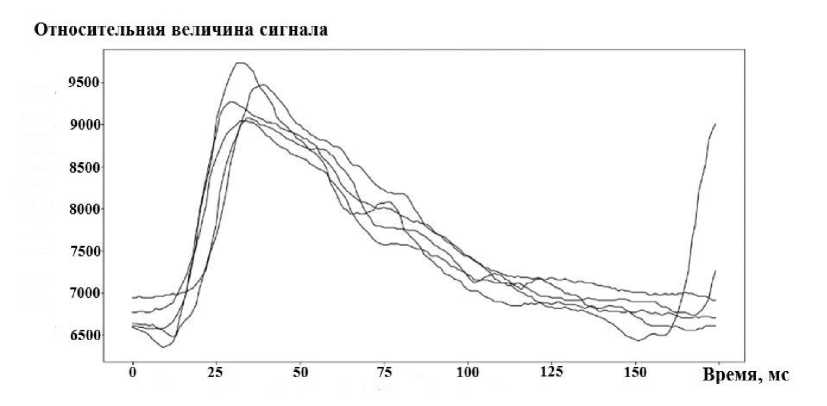
Рис. 9. Пример пульсовых волн испытуемых из кластера 3

средние пульсовые волны

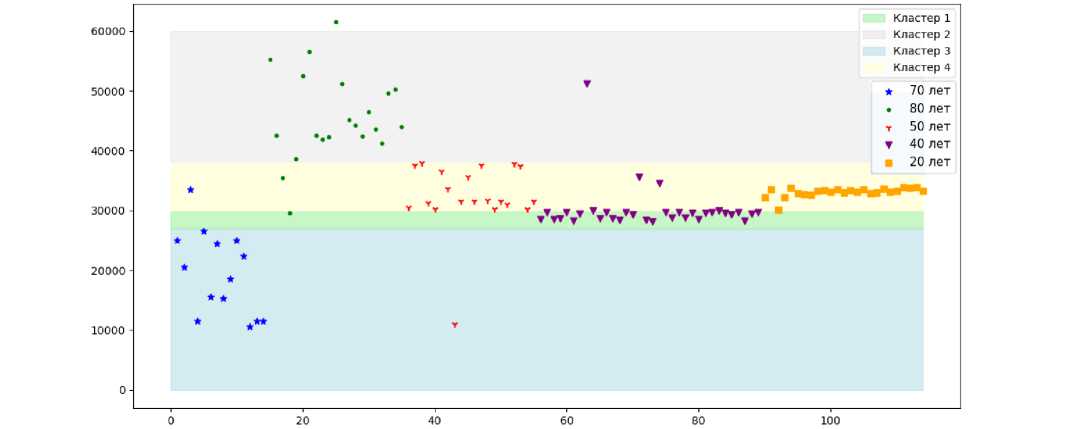
пациенты

Рис. 10. Распределение возрастов испытуемых по сравнению с 4 кластерами: OX – порядковые номера испытуемых; OY – среднее значение ПВ

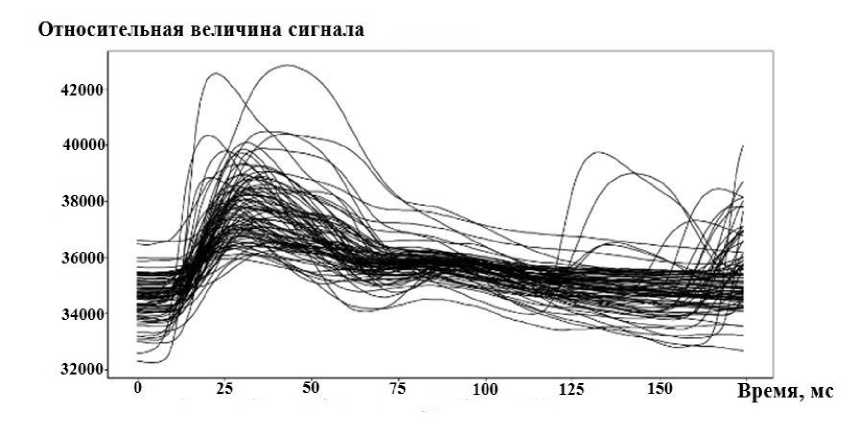
Рис. 11. Пример пульсовых волн испытуемых из кластера 1

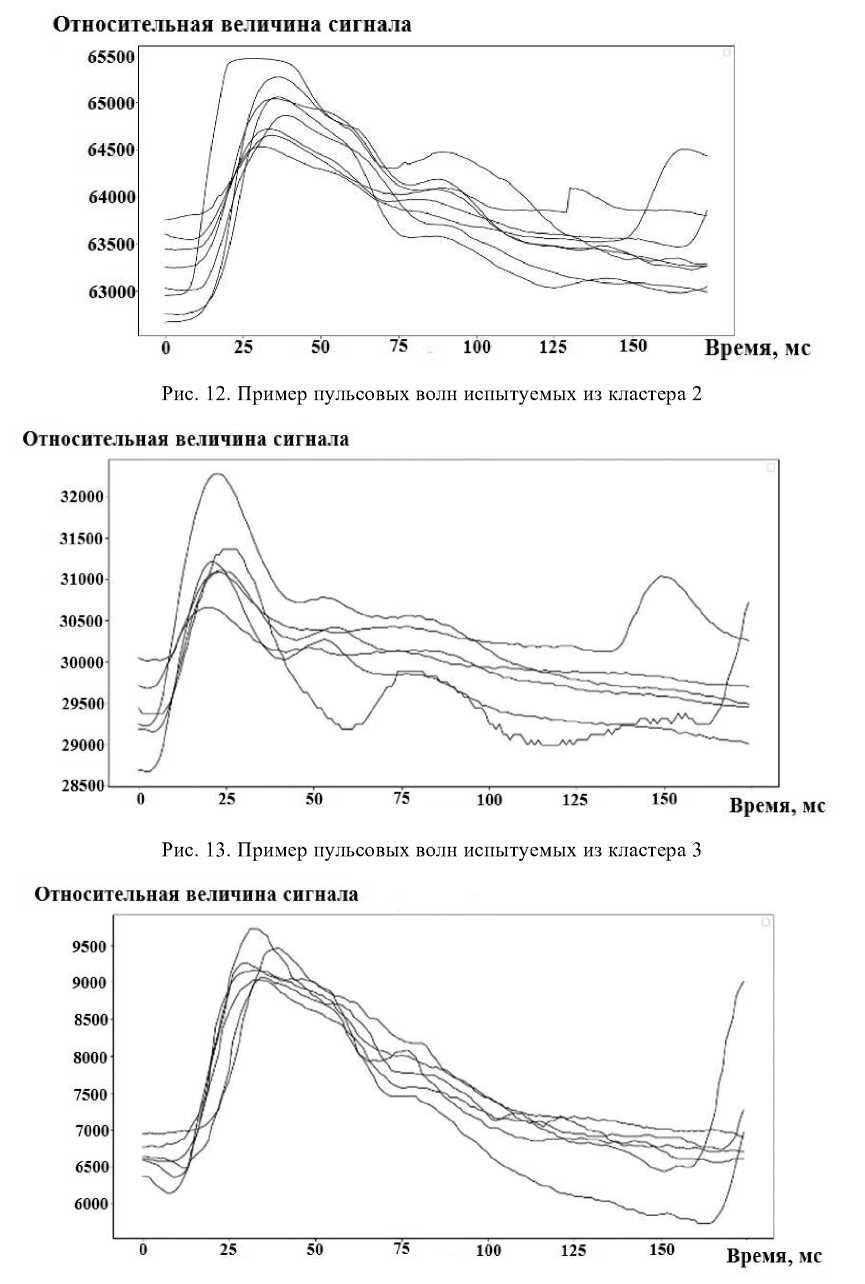
Рис. 14. Пример пульсовых волн испытуемых из кластера 4

В табл. 4 приведены результаты, которых достигает алгоритм SOM для кластеризации всех возрастов. Эта кластеризация может служить для определения границы между кластерами. В табл. 5 показаны параметры сетей Кохонена в каждой серии экспериментов для пяти кластеров.

Таким образом, в результате экспериментов с различными конфигурациями нейронных сетей были получены различные структуры кластеров. Суть предлагаемой методологии заключается в том, чтобы выбрать такие параметры нейронной сети, которые лучше других соответствуют реальным данным. В

Таблица 3

Результаты кластеризации испытуемых в четыре кластера с использованием алгоритма SOM .

Возраст, лет	Кластер 1, абс. / %	Кластер 2, абс. / %	Кластер 3, абс. / %	Кластер 4, абс. / %
20	18/19, 94	0	1/19, 6	0
40	2/34, 5	30/34, 95	0	1/34, 2
50	21/22, 96	0	0	1/22, 4
70	1/15, 7	0	0	14/15, 93
80	1/23, 4	1/23, 4	21/23, 91	0

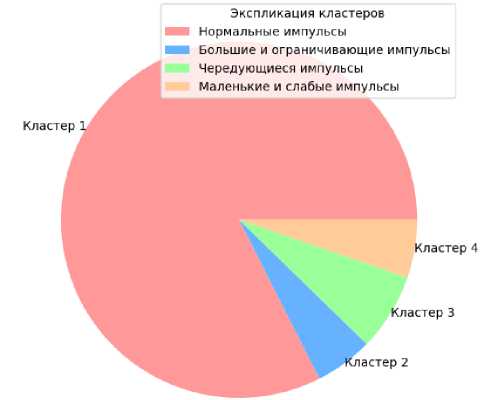
Рис. 15. Экспликация кластеров. Распределение возрастов испытуемых по кластерам в соответствии

с характеристиками пульсовых волн средние пульсовые волны

пациенты

Рис. 16. Распределение возрастов испытуемых по сравнению с 5 кластерами: OX – порядковые номера испытуемых; OY – среднее значение ПВ

дальнейшем эту сеть можно использовать в диагностических системах поддержки принятия врачебных решений. Достаточно простая программная реализация обученной нейронной сети и портативность прибора измерения пульсовой волны позволяют применять предлагаемый метод для мониторинга состояния сердечно-сосудистой системы, что актуально для людей, которые находятся в зоне риска сердечно-сосудистых катастроф или связаны с опасными профессиями (пожилые люди, машинисты электропоездов и др.), для спортсменов, офисных работников и др. Регистрация изменения биологического возраста в ту или иную сторону способствует принятию своевременных решений, в том числе по коррекции питания, образа жизни и физической активности.

Таблица 4

Результаты кластеризации испытуемых в пять кластеров с использованием алгоритма SOM

Возраст, лет	Кластер 1, абс. / %	Кластер 2, абс. / %	Кластер 3, абс. / %	Кластер 4, абс. / %	Кластер 5, абс. / %
20	1/19, 5	0	17/19, 90	1/19, 5	0
40	0	31/34, 91	2/34, 6	0	1/34, 2
50	1/22, 5	0	1/22, 5	20/22, 90	0
70	14/15, 93	0	1/15, 7	0
80	0	1/23, 4	1/23, 4	0	21/23, 91

Таблица 5

Параметры сетей Кохонена в каждой серии экспериментов

Тип кластеризации	два кластера	три кластера	четыре кластера	пять кластеров
Размерность SOM	1 x 2	1 x 3	1 x 4	1 x 5
Параметр σ	0,5	0,5	0,5	0,5
Параметр α	0,5	0,6	0,6	0,6
Максимальное количество итераций	500	400	500	600

Обсуждение

сти кластеризации, которая в ряде случаев имеет точность более 90 %.

Оценка биологического возраста человека важна для контроля процессов старения. Регулярный мониторинг этого показателя позволяет вовремя принимать меры профилактики, снижающие риски сердечнососудистых катастроф, т. е. управлять рисками нарушения здоровья и заболеваний сердечно-сосудистой системы. Данное исследование носит методологический характер и описывает подход к исследованию сердечнососудистой системы человека. Нейросетевые алгоритмы и машинное обучение традиционно используются для получения новых знаний из больших биомедицинских данных и задач биомеханики. В данном исследовании мы применили алгоритм кластерного анализа на основе самоорганизующейся нейронной сети Кохонена для того, чтобы исследовать собранную статистику о формах механопульсограмм с тем, чтобы систематизировать полученную информацию и привязать её к биологическим процессам старения сердечно-сосудистой системы человека. Очевидно, к исследованию пульсовых волн можно применять различные методы машинного обучения, вейвлет- и Фурье-анализ, а также другие методы. В результате проведённых исследований сделан вывод, что механопульсограммы содержат в себе информацию о биологическом возрасте, но требуются дополнительные статистические данные, чтобы развить этот метод и сделать распознавание биологического возраста более точным.

Заключение

Основываясь на результатах исследования, можно сделать вывод, что сети Кохонена могут группировать пульсовые волны в различные значимые кластеры. Результат указывает на высокий уровень эффективно-

Кластерный анализ пульсовых волн человека позволяет определять маркеры, которые связаны с геометрией и формой пульсовых волн человека. По сравнению с другими алгоритмами кластеризации, нейросетевая кластеризация является в значительной степени более гибким инструментом кластерного анализа за счёт структуры и параметров и нейронной сети Кохонена. За счёт подстроек параметров нейронной сети этот алгоритм позволяет получить такие кластеры, которые отражали бы объективную картину, формируя так называемые информативные кластеры. Целью настоящего исследования является поиск и обучение структур нейронных сетей Кохонена для определения возрастных групп по пульсовым волнам испытуемых. В результате серии проведённых вычислительных экспериментов были получены нейронные сети Кохонена с их топологиями и структурами связей, которые позволяют выявлять возрастные группы, исключительно основываясь на анализе геометрии пульсовой волны.

Нельзя сказать, что эти полученные кластеры в полной мере отражают объективные характеристики. Однако в ряде случаев по кластеру можно определить возрастную группу. Таким образом, гипотеза исследования подтвердилась, и в пульсовых волнах исследованных испытуемых находятся маркеры возрастных групп, которые можно выявить сетями Кохонена. Для дальнейших исследований требуется увеличенный набор пульсовых волн для более объективной и всесторонней оценки данных с помощью описанного метода.

Обобщая все вышесказанное, отметим, что нейросетевой подход для кластеризации на основе са- моорганизующихся карт Кохонена является перспективным методом исследования сложных динамических