Кластеризация с использованием методов удовлетворения табличных ограничений

Использование дополнительных ограничений в процессе интеллектуального анализа данных может быть полезно на всех этапах работы: как для предобработки информации, повышения производительности алгоритмов обработки, так и для анализа и уточнения результатов [1]. В частности, анализ подобных знаний способствует повышению эффективности и точности результатов рассматриваемых в работе задач кластеризации, а также повышению доверия экспертов к результатам кластеризации [2]. Знания могут быть представлены различным образом: в виде подмножества помеченных объектов, т.е. объектов, которым заранее присвоена метка класса; в форме ограничений на присут- ствие/отсутствие тех или иных подмножеств объектов в кластерах; как требования к размеру кластеров и т.п.

В настоящее время развивается подход к кластеризации, именуемый кластеризацией с частичным привлечением учителя [3], в котором при отнесении объектов к одному или различным кластерам анализируются не только расстояния между объектами, но и некоторые фоновые знания из предметной области (ПрО). Традиционный подход к решению задач кластеризации с частичным привлечением учителя состоит в модификации существующих методов кластеризации, большинство из которых является методами локального поиска, поэтому данный подход позволяет находить лишь локальный оптимум [4].

Целью представленных исследований является разработка нового подхода к поиску глобального оптимума при решении задач кластеризации с частичным привлечением учителя, опирающегося на комплексный учёт разнородных экспертных знаний о ПрО. Подход направлен на снижение степени неопределённости при получении результатов анализа данных.

Предлагаемый подход реализован в рамках технологии программирования в ограничениях, которая основывается на широком спектре методов искусственного интеллекта, информационных технологий и исследования операций [5]. Особенность подхода состоит в моделировании задач кластеризации с использованием специализированных табличных ограничений и широком применении процедур вывода на данных ограничениях при поиске требуемого разбиения.

Подробное описание видов табличных ограничений и их классификацию можно найти в [6], а описание применения табличных ограничений для решения задачи поиска в больших данных паттернов заданного вида содержится в [7]. Настоящая работа продолжает исследования, посвящённые применению процедур вывода на табличных ограничениях при решении задач машинного обучения.

• 1    Ограничения в задаче кластеризации

Кластеризация – это процесс разделения набора объектов на подмножества таким образом, чтобы объекты из одного кластера были более похожи друг на друга, чем на объекты из других кластеров, по какому-либо критерию. К наиболее известным методам кластеризации относятся метод K -средних, иерархические методы, спектральная кластеризация [8-10].

Отнесение двух объектов в один кластер только на основе метрики может быть семантически некорректной операцией [2]. Недостатком большинства существующих методов кластеризации является невозможность гибко учитывать пользовательские ограничения на объекты кластеризации и искомую модель. Применение фоновых знаний положительно влияет на процесс решения задачи кластерного анализа, повышая его эффективность за счёт дополнительной редукции пространства поиска и обеспечивая возможность получения глобального оптимума (в случае необходимости) за приемлемое время.

При решении задачи кластеризации целесообразен учёт следующих ограничений.

Пользовательские ограничения могут быть двух уровней: на объекты кластеров , уточняющие требования к парам конкретных объектов; на кластеры , указывающие требования к кластерам.

Самыми распространенными ограничениями на объекты кластеров являются ограничения на пары объектов, они бывают двух типов [11, 12]: «обязательно связаны» и «не могут быть связаны». Первые требуют, чтобы два экземпляра были размещены в одном кластере, а вторые предписывают размещение двух экземпляров в разных кластерах. Ограничения «обязательно связаны» являются симметричными, рефлексивными и транзитивными. Ограниче- ния «не могут быть связаны» не обладают свойством транзитивности. Обычно подобные ограничения применяются на этапе интеллектуального анализа и определяются как жёсткие, но могут быть ослаблены, если пользователь выражает неуверенность в конкретном ограничении. Применение этих ограничений зачастую приводит к повышению точности результата, и они могут использоваться для выражения других пользовательских ограничений.

Ограничения на кластеры могут задаваться через пространственные свойства. Например, ограничение на максимальный диаметр разбиения, которое определяет верхнюю границу диаметра кластера и означает, что между каждой парой объектов любого кластера расстояние не может превышать эту границу. Это ограничение может рассматриваться как конъюнкция ограничений «не могут быть связаны» между всеми парами объектов с расстоянием, превышающим границу. Распространённым является ограничение, задающее минимальное расстояние между объектами различных кластеров. Данное ограничение может быть выражено как конъюнкция ограничений «обязательно связаны» между всеми парами объектов, расстояние между которыми меньше, чем заданная нижняя граница.

Примеры ограничений на кластеры:

• ■    минимальная мощность (населённость) кластера означает, что число объектов в каждом кластере должно быть не меньше заданной границы а ;

• ■    максимальная мощность кластера означает, что число объектов в каждом кластере должно быть не больше заданной границы в ;

• ■    средняя населённость кластера означает, что должен соблюдаться баланс, и все кластеры должно быть примерно одного размера, т.е. отношение между размером самого маленького и самого большого кластеров должно быть больше заданной границы в.

• ■    ограничение на плотность кластера предписывает, что в радиусе е каждого элемента должен существовать другой объект, принадлежащий данному кластеру.

Способом привлечения фоновых знаний является также использование небольшого набора помеченных объектов, т.е. объектов, которым присвоена метка кластера, в который они должны попасть. В [13] используется множество объектов, которыми «засеиваются», т.е. инициализируются кластеры, а также ограничения, которые генерируются на основании помеченных данных. Удачным образом произведённая инициализация в дальнейшем может помочь алгоритму избежать «застревания» в локальном оптимуме, поскольку соответствует пользовательскому определению кластеров.

• 2    Методы кластеризации с частичным привлечением учителя

Методы кластеризации с частичным привлечением учителя можно поделить на три категории, основанные на: расстоянии, ограничениях, ограничениях и расстоянии [3].

В подходах, основанных на ограничениях, алгоритм кластеризации модифицируется для интеграции попарных ограничений («обязательно связаны» и «не могут быть связаны»), тогда как в подходах, основанных на расстоянии, изменяется только метрика расстояния.

Алгоритм Constrained k-means ( Cop-k-means ) [14] - это алгоритм кластеризации с частичным привлечением учителя, который является модификацией алгоритма k-means [15], использующей попарные ограничения, т.е. кластеризуемый объект данных должен удовлетворять ограничениям «обязательно связаны» и «не могут быть связаны».

Пусть набор данных нужно разделить на к=2 кластера Cl 1 и Cl ₂, и 1 и и ₂ являются центральными точками каждого кластера, а O i и O j - два экземпляра данных (объекта), на которые наложено ограничение «обязательно связаны». Если O i отнесён к ближайшему кластеру Cl 1 , алгоритм Cop-k-means не вычисляет расстояние между объектом O j и центральными точками кластеров, а напрямую относит O j к кластеру Cl 1 . Это происходит даже несмотря на то, что O j может находиться ближе к центральной точке кластера Cl ₂. Также можно ввести ограничения на объекты, модифицировав метрику расстояния или целевую функцию.

Алгоритм BH-k-means является модификацией алгоритма k-means [16]. В нём объединены ограничения «обязательно связаны» и «не могут быть связаны», и на каждой итерации, когда происходит обновление разбиения, эти ограничения должны удовлетворяться. Целевая функция данного алгоритма состоит из двух частей: первая вычисляет евклидово расстояние между объектами и центрами кластеров, вторая - штраф за нарушение ограничений.

Методы, основанные на модификации метрики, изменяют значение расстояния, исходя из анализа фоновых знаний. Идея заключается в том, что если на два объекта O i и O j накладывается ограничение «обязательно связаны», то расстояние между ними может быть меньше обычного, чтобы у них было больше шансов оказаться в одном кластере. Похожий подход применяется и к ограничению «не могут быть связаны».

Одним из таких алгоритмов является MK-means ( Metric K-means ) [17], в котором минимизируются квадраты расстояний между объектами, связанными ограничением «обязательно связаны». В MPCK - means ( Metric Pairwise Constrained K-means ) [17] объединены подходы, основанные на ограничениях и на метриках, и, в отличие от MK-means , используются не только ограничения, но и непомеченные данные для вычисления метрики. Для каждого кластера допускается своя метрика, поэтому кластеры могут принимать различные формы. Сумма штрафа всегда одинакова, однако нарушение ограничения «обязательно связаны» для удалённых друг от друга объектов является более серьёзным, чем нарушение этого же ограничения для близлежащих объектов. Поэтому каждый штраф умножается на среднее расстояние между двумя объектами. Аналогичная ситуация с ограничением «не могут быть связаны». В упомянутом в разделе 1 методе «засеивания» для кластеризации используется помеченные данные [13, 18]. В данном подходе используются алгоритм k-means со штрафами и алгоритм «засеивания». Метод «засеивания» позволяет решить задачу поиска начальных центров кластеров. За неверно кластеризованные объекты предусмотрены штрафы.

• 3    Организация вывода на табличных ограничениях

Задача удовлетворения ограничений (ЗУО) состоит из конечного множества переменных V ={ x 1 , ..., x_n }, множества доменов этих переменных Dom ={ Dom i , ..., Dom_n } и множества ограничений Constr , которые определяют допустимые комбинации значений переменных [5]. Решением ЗУО называется кортеж значений ( d 1 , ..., d_n ), которые удовлетворяют всем ограничениям ( d i е Dom i ).

Перспективным подходом к представлению и обработке качественных зависимостей (логических формул, продукционных правил и т.п.) в рамках парадигмы программирования в ограничениях следует признать подход, основанный на применении их специализированного табличного представления. Известные виды табличных ограничений, такие как обычные таблицы, сжатые таблицы и смарт-таблицы [19], хорошо подходят для моделирования дизъюнктивных нормальных форм логических формул. Однако с их помощью не всегда целесообразно описывать некоторые виды знаний, например, продук- ционные правила, поскольку при этом порождаются громоздкие конструкции.

Любое ограничение, определённое на конечных доменах переменных, может быть представлено в виде обычной таблицы.

X 1 X 2 X 3

’ 4 2 3 1

7 2 3

7 5 3

Пример 1 . Пусть ограничения заданы в виде предиката ( X 1 > X г ) л ( X 1 + X 3 < 10), а домены переменных X i e {1, 4, 7}, X ? е {2, 5, 8}, X 3 е {3, 9}. В виде таблицы данное отношение будет иметь вид (см. справа). В таблице явно перечислены все допустимые присваивания для ограничения. Но при таком эксплицитном представлении размер таблиц будет расти экспоненциально при росте количества атрибутов и размеров их доменов.

X1  X2

Данную таблицу можно переписать в виде сжатой таблицы: {4}  {2}{3}

{7} {2,5} {3}

X1X2

Данное ограничение в виде смарт -таблицы C -типа [6, 7] имеет вид:

[ >=

.

Пример 2 . Пусть задано некоторое правило (3> L )^( G i ^ G ₂). Раскрытие в данном выражении импликации приводит к записи: (3 < L )v( G 1 ^ G ₂). С помощью известных типов смарт -таблиц это ограничение может быть выражено следующим образом [6, 7]:

L G 1 G 2

’> 3    * ' .

*     ^

Приведённое табличное ограничение содержит заголовок отношения/ограничения, куда входит один простой атрибут L и составной атрибут G 1 G ₂. В каждом столбце таблицы содержится одна значащая компонента и одна фиктивная компонента «*», которая описывает весь диапазон возможных значений соответствующего атрибута. В написании компонент может использоваться символ «∅», который обозначает компоненту, не содержащую ни одного значения.

В отличие от смарт -таблиц С -типа, которые соответствуют дизъюнктивным нормальным формам логических формул с элементарными одно- и двухместными предикатами, смарт -таблицы D -типа соответствуют конъюнктивным нормальным формам таких формул. Смарт- таблицы D -типа записываются при помощи обратных квадратных скобок.

Представленное выше правило может быть смоделировано следующей смарт -таблицей D -типа, состоящей из одной строки:

L G 1 G ₂ ] > ³     * [ .

Вывод (распространение) на ограничениях, представленных в виде смарт -таблиц D -типа, предлагается осуществлять с использованием следующих утверждений [7].

Утверждение 1 . Если хотя бы одна строка смарт -таблицы D -типа пуста (содержит все пустые компоненты), то таблица пуста (соответствующая задача удовлетворения ограничений не имеет решения).

Утверждение 2 . Если все компоненты некоторого атрибута пусты, то данный атрибут можно удалить из смарт -таблицы D -типа (удаляются все компоненты, стоящие в соответствующем столбце), а пара «удаляемый атрибут - его домен» сохраняется в векторе частичного решения.

Утверждение 3 . Если в смарт -таблице D -типа есть строка ( смарт -кортеж), содержащая лишь одну непустую компоненту, то все значения, не входящие в эту компоненту, удаляются из соответствующего домена.

Утверждение 4 . Если строка смарт -таблицы D -типа содержит хотя бы одну полную компоненту, то строка удаляется.

Утверждение 5 . Если компонента атрибута смарт -таблицы D -типа содержит значение, не принадлежащее соответствующему домену, то значение удаляется из компоненты.

Утверждение 6 . Если в смарт -таблице D -типа усечён один или несколько доменов простых атрибутов, которые формируют некоторый составной атрибут, то из домена составного атрибута исключаются отношения, которые обращаются в пустое множество при новых доменах соответствующих простых атрибутов.

Утверждение 7 . В случае конкретизации домена составного атрибута должны быть конкретизированы и домены соответствующих простых атрибутов с учётом вновь выведенного домена составного атрибута.

Далее рассматривается применение вывода на табличных ограничениях для решения задачи проверки логического следования предиката P ( x ) из предиката Q ( x ), т.е. Q ( x ) |= P ( x ), где ^ - знак логического следования.

Всякий n -местный предикат P ( x 1 , x ₂, ..., x_n ) можно рассматривать как одноместный P ( x )

на множестве наборов ( m i , m 2, ..., m n ) е M i x M ₂ x _ x M n .

Пусть предикат P ( x ) задан на ПрО M . Тогда ему можно поставить во взаимно однозначное соответствие подмножество M_P тех элементов x * е M , для которых значение P ( х* ) истинно: P ( х* )= true о х * е M_p и P ( х* )= false о х * е M\M P . Аналогичным образом интерпретируется отрицание предиката P ( х): — P ( х* )= true о х * е M\M P .

Для предикатов P ( х ) и Q ( х ) при любом значении х * предметной переменной х справедливы соотношения: P ( х* )v Q ( х* )= true о х * е M P о M q ; P ( х* ) л Q ( х* )= true о х * е M_P ^ M q .

Теоретико-множественная интерпретация отношения логического следования состоит в следующем: P ( х ) |= Q ( х ) о M P ^ M q . Из логики известно, что доказательство соблюдения логического следования P ( х ) |= Q ( х ) часто проверяется согласно следующему соотношению: P ( х ) л— Q ( х )^, т.е. сводится к доказательству противоречивости формулы P ( х ) л— Q ( х ), которая на языке алгебры множеств выражается следующим образом: M P n ( M\M q )= 0 .

Таким образом, подтверждение или опровержение логического следования P ( х ) |= Q ( х ) может выполняться путём вычисления алгебраических выражений, в которых задействованы области истинности M P и M q этих предикатов. Подобные вычисления не эффективны, если области M P и M q представлены с помощью обычных таблиц истинности, но если эти области выражаются с помощью смарт -таблиц, то ситуация в корне изменяется.

Пример 3 . Пусть имеются два предиката P ( X , Y ) = ( X е {1, 2}) л ( Y е {3, 4}) и Q ( X , Y ) = ( X л Y ), где области определения переменных X и Y совпадают и равны множеству M ={1, 2. 3. 4}. Требуется определить, выполняется ли соотношение P ( х ) |= Q ( х ).

Решение сводится к проверке противоречивости следующей формулы

P ( х ) л— Q ( х )=( X e {1, 2}) л ( Y е {3, 4}) л ( X = Y ).

Противоречивость/непротиворечивость данной формулы сводится к установлению с использованием утверждений 6,7 пустоты следующей смарт -таблицы C -типа, моделирующей текущее состояние доменов переменных (как простых, так и составных):

X Y XY

[{1,2} {3,4} = ].

Данная таблица пуста, следовательно логическое следование P ( х ) ^ Q ( х ) выполняется.

Пример 4 . Пусть P ( X i , X ,>( X ₍ е {2}) л ( X i = X 2 ), а Q ( X 1 , X , ) ^ ( X ₍ e {2})v( X ₂ е {3, 4}) л ( X 1 # X 2 ). Требуется определить, выполняется ли соотношение P ( х ) |= Q ( х ).

С помощью смарт -таблиц С -типа выражение M P ^ M q для этого случая имеет вид:

X ₁ X 2 X ₁ X ₂ X ₁ X ₂ X ₁ X ₂

[ {2}   *

{2}    *

*   {3,4}

*

л

Данное соотношение выполняется, поскольку однострочная смарт-таблица, стоящая слева от знака включения множеств, покомпонентно содержится в первой строчке смарт-таблицы, стоящей справа от этого знака. Значит, логическое следование выполнено.

Следует отметить, что все алгебраические операции и проверки соотношения включения выполняются для смарт -таблиц без их разложения в элементарные кортежи.

• 4    Задачи кластеризации в парадигме программирования в ограничениях

Пусть требуется разбить заданные объекты O ={ 0 ₁, ..., O n } на k е [ k_min , k_max ] непересекаю-щихся кластеров таким образом, чтобы минимизировать диаметр разбиения ( Diam ^ min ). Диаметр разбиения - это максимальное в рамках разбиения расстояние между любыми двумя точками, принадлежащими одному кластеру.

За базовую модель для решения задачи кластеризации с частичным привлечением учителя принята модель, описанная в [2]. В данной модели переменные O ={ O i , ..., O n } соответствуют объектам кластеров, а в качестве их доменов выступает множество индексов возможных кластеров {1, ..., k max } . Присваивание O i = c , где c е {1, ..., k max }, означает, что точка O i попадает в кластер c . Полное присваивание переменных представляет собой разбиение.

При постановке задачи необходимо задать следующие основные ограничения.

• ■   Precede ( O , [1, ..., k max ]) - ограничение, исключающее симметричные решения: каждому

из возможных разбиений, содержащих, по меньшей мере, k min различных кластеров и самое большее k max различных кластеров, должно соответствовать ровно одно полное присваивание значений переменных.

• ■   AtLeast ( O , k min , 1) - ограничение предписывает, чтобы в результирующем полном при

сваивании хотя бы одна из переменных O ={ 0 ₁, ..., O n } принимала значение k min . Условие на верхнюю границу k max интервала для k учитывается при задании множества возможных индексов кластеров - {1, _, k_max }.

• ■    При решении задачи минимизации диаметра разбиения для каждой пары объектов, т.е. для каждого элемента матрицы расстояний [ d ij ], должно быть сгенерировано ограничение вида

( d ij > Diam )^( O i * O j ).                              (1)

Здесь d ij - это константа, обозначающая расстояние между объектами O i и O j . Переменная Diam обозначает диаметр разбиения и изначально принимает значения из интервала [ d_min , d_max ], где d_min и d_max - это минимальный и максимальный элементы матрицы [ d ij ].

В задаче кластеризации с частичным привлечением учителя пользователь может задать дополнительные ограничения, которые также интегрируются в модель [2]:

• ■    ограничение на минимальное количество а элементов в кластере O i : AtLeast ( O , O i , a );

• ■    ограничение на максимальное количество в элементов в кластере c : AtMost ( O , c , в );

• ■    бинарное ограничение «обязательно связаны» O i = O j , задающее, что пара объектов O i и O j должна попадать в один кластер при любом варианте разбиения [11];

• ■    бинарное ограничение «не могут быть связаны» O i * O j , задающее, что пара объектов O i и O j не попадает в один кластер при любом варианте разбиения [12].

Совокупности ограничений вида (1) в настоящей статье предлагается моделировать с помощью смарт -таблиц D -типа.

• 5    Пример решения задачи кластеризациис использованием вывода на табличных ограничениях

  Пример 5 . Пусть имеется пять объектов, которые нужно разбить на два кластера, т.е. k =2. Задана матрица расстояний между объектами (см. таблицу 1). Необходимо найти разбиение объектов с минимальным диаметром. Пусть первый объект принадлежит первому кластеру ( 0 ₁=1).

  Ограничения на основе значений, приведённых в матрице расстояний, имеют вид:

  
  

  Таблица 1 - Пример матрицы расстояний для задачи разбиения на два кластера

  	0 1	O 2	O з	O 4	O 5
  0 1	0	8	15	3	1
  O 2	8	0	1	7	2
  O 3	15	1	0	2	3
  O 4	3	7	2	0	1
  O 5	1	2	3	1	0

  
  

( Diam <  8) ^ ( O * O ₂)

( Diam <  15) ^ ( O * O ₃)

( Diam <  3) ^ ( O 1 * O ₄)

( Diam <  1) ^ ( O * O ₅)

( Diam <  1) ^ ( O ₂ * O ₃)

( Diam <  7) ^ ( O₂ * O₄)

( Diam <  2) ^ ( O ₂ * O ₅)

( Diam <  2) ^ ( O ₃ * O ₄)

( Diam <  3) ^ ( O ₃ * O ₅)

( Diam <  1) ^ ( O ₄ * O ₅) .

Раскрытием импликации получаются следующие дизъюнкции:

( Diam >  8) v ( O 1 * O ₂)

( Diam >  15) v ( O 1 * O ₃)

( Diam >  3) v ( O 1 * O 4 )

( Diam >  1) v ( O 1 * O ₅)

( Diam >  1) v ( O ₂ * O ₃)

( Diam >  7) v ( O ₂ * O ₄)

( Diam >  2) v ( O ₂ * O ₅)

( Diam >  2) v ( O ₃ * O ₄)

( Diam >  3) v ( O ₃ * O ₅)

( Diam >  1) v ( O ₄ * O ₅)

Данные ограничения также могут быть Diam O 1 O2   O 1 O3 O 1 O 4 O 1 O 5						записаны в виде смарт -таблицы D O 2 O 3   O 2 O 4    O 2 O 5 O 3 O 4 O 3 O 5					типа: O 4 O 5
1 ’	> 8	*	0	0	0	0	0	0	0	0	0 -
2	> 15	0	*	0	0	0	0	0	0	0	0
3	> 3	0	0	*	0	0	0	0	0	0	0
4	> 1	0	0	0	*	0	0	0	0	0	0
5	> 1	0	0	0	0	*	0	0	0	0	0
6	> 7	0	0	0	0	0	*	0	0	0	0
7	> 2	0	0	0	0	0	0	*	0	0	0
8	> 2	0	0	0	0	0	0	0	*	0	0
9	> 3	0	0	0	0	0	0	0	0	*	0
10 .	> 1	0	0	0	0	0	0	0	0	0	*  _

Процедура поиска минимального диаметра разбиения следующая. Изначально домен переменной, описывающий диаметр разбиения, равен множеству {1, 2, 3, 4, 7, 8, 15}. На первом шаге можно предположить, что Diam =1. Тогда видно, что строки 4, 5 и 10 исключаются из рассмотрения на основании утверждения 4, поскольку их компонента Diam становится полной. С учётом утверждения 5 все оставшиеся компоненты столбца Diam становятся пустыми. Остаток в виде смарт -таблицы D -типа имеет вид:

Di	am = 1	O 1 O 2	O 1 O 3	O 1 O 4	O 1 O 5	O 2 O 3	O 2 O 4	O 2 O 5	O 3 O 4	O 3 O 5	O 4 O 5
1 ■	0	*	0	0	0	0	0	0	0	0	0
2	0	0	*	0	0	0	0	0	0	0	0
3	0	0	0	*	0	0	0	0	0	0	0
6	0	0	0	0	0	0	*	0	0	0	0
7	0	0	0	0	0	0	0	*	0	0	0
8	0	0	0	0	0	0	0	0	*	0	0
9	0	0	0	0	0	0	0	0	0	*	0

В результате упрощения данной таблицы согласно утверждению 3 вычёркиваются все строки смарт -таблицы D -типа. Здесь и далее для моделирования текущего состояния доменов простых и составных переменных (текущего частичного присваивания) используются смарт -таблицы С -типа, состоящие из единственной строки. Для данного случая получается следующее частичное присваивание:

O ₁ Diam O ₁ O ₂   O₁O₃ O ₁ O ₄ O₂ O₄ O₂ O₅  O₃ O₄ O₃ O₅

[ {1}  {1}       *      *     *      *     *      *      * ] •

Первый столбец описывает тот факт, что объект 0 1 принадлежит первому кластеру ( O 1 =1). Этот факт здесь и далее добавлен для исключения симметрии в получаемых решениях. Из анализа полученной смарт -таблицы С -типа (утверждения 6 и 7 ), во-первых, следует, что объект O 1 должен лежать в разных кластерах с объектами O 2 и O 4 , а, во-вторых, что объекты O 2 и O 4 не могут лежать в одном кластере. Эти два условия не могут быть одновременно удовлетворены при количестве кластеров равном двум. По той же причине минимальное значение диаметра разбиения не может быть равно 2.

Проверка Diam =3 для заданной системы ограничений приводит к следующему частичному присваиванию:

O ₁ Diam O₁O₂ O ₁ O ₃ O₂ O₄

[ {1}    {3}       *      *       * ] .

Фактически данная смарт-таблица С-типа моделирует следующую логическую форму лу: (01=1)л(Diam=3)л( O1* O 2)л( O1* O з)л( O 2* O 4).

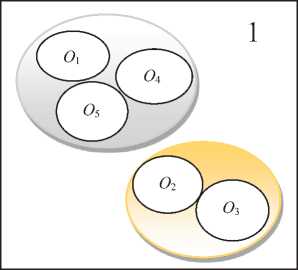
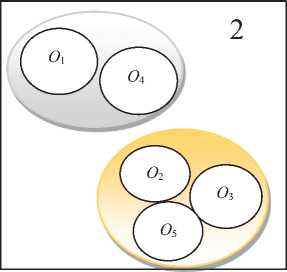
Рисунок 1 - Варианты разбиения

При таком диаметре возможны два решения. Полученные разбиения представлены на рисунке 1.

Решение задачи кластеризации на основе разработанной декларативной модели осуществляется с применением систематического поиска. В ходе систематического поиска не происходит полного перебора вариантов, поскольку неперспективные ветви дерева поиска отсекаются в результате применения метода распространения ограниче- ний и предложенных правил выбора наилучшего преемника текущего состояния. Предлагаемый метод систематического поиска опирается на следующие эвристики выбора переменной на текущем шаге поиска: выбирается переменная, домен которой содержит наименьшее количество значений. При выборе значения переменной применяется следующее правило: поскольку переменная представляет один из кластеризуемых объектов, а её значение - номер кластера, то переменной присваивается номер того кластера, который ближе к рассматриваемому объекту.

• 6    Пример решения задачи кластеризациис частичным привлечением учителя

Представление знаний в виде смарт -таблиц D -типа может быть полезно не только при обработке правил вида (1), но и при работе с некоторыми дополнительными пользовательскими ограничениями, например с ограничением на плотность кластера.

Пример 6 . Пусть к исходным условиям задачи кластерного анализа, описанной в примере 1 , добавлено ограничение, что на расстоянии 1 от любого объекта кластера должен находиться хотя бы один другой элемент этого же кластера. Пусть объект O 1 отнесён пользователем в первый кластер ( O 1 =1), а объект O 3 - во второй кластер ( O ₃=2). Целью (по-прежнему) является минимизация диаметра разбиения. В данном случае ограничение на плотность описывается следующей смарт -таблицей D -типа:

O1O5  O2 O3

• ■ =   00’

0   =

0   =

0   0

• .  =    0    =_

.

Каждая строка данной таблицы соответствует дизъюнкции ограничений «обязательно связаны» для некоторого объекта. Поскольку кластеризуемых объектов пять, то и количество строк матрицы равно пяти. Например, последняя строка матрицы соответствует ограничению: ( O ₅= O i )v( O ₅= O ₄), т.е. вместе с O ₅ в одном кластере должен находиться либо объект O 1 , либо объект O 4 , либо они оба, поскольку их расстояние до O 5 равно 1.

Таблицу, моделирующую данное пользовательское ограничение, можно упростить, используя утверждения 1-5: все строки данной таблицы вычёркиваются, а текущее частичное присваивание описывается следующей однострочной смарт -таблицей C -типа:

O O ₅ O ₂ O ₃   O ₄ O ₅

[ =      =      = ]

.

Добавление к данной упрощённой таблице, моделирующей ограничение на плотность, пользовательских ограничений для объектов O 1 и O ₃, приводит к следующей смарт -таблице С -типа:

O 1 O 3   OO O 2 O 3 O O ,

[ {1} {3}    =       =      = ]

.

На основе её анализа с учётом утверждений 6, 7 получается следующая смарт -таблица C -типа:

О,  O2  O, O4  O,  OO,  O, O3

[{1) {2} {2} {1} (1}    =     ==

Анализируя данную таблицу, можно конкретизировать значения всех составных атрибутов:

OO2  OO3   O1O4  O2 O4  O2 O,   O3 O4

[ *    *     =     *     *      **

Из таблицы, где содержатся выражения вида (1), формализующие базовые ограничения задачи кластеризации, видно, что с учётом новых доменов составных атрибутов в ней часть строк вычёркивается, а оставшиеся строки будут содержать ровно по одной непустой компоненте каждая (компонента Diam ):

Diam	O 1 O 2	OO 3	O 1 0 4	OO 5	O 2 O 3	O 2 O 4	O 2 O	O 3 O 4	O 3 O ,	O 4 O ,
■ >  1	0	0	0	0	0	0	0	0	0	0"
> 1	0	0	0	0	0	0	0	0	0	0
> 3	0	0	0	0	0	0	0	0	0	0
> 1	0	0	0	0	0	0	0	0	0	0_

Это означает, что нижняя граница домена переменной Diam устанавливается в значение «3». Ответом задачи является следующее разбиение с минимальным диаметром равным Diam =3: O i =1, O₂=2, O 3 =2, O ₄=1, O ₅=1, которое изображено на рисунке 1 слева.

• 7 Определение множества «мигрирующих» объектов и «ядер» кластеров

Если предположить, что имеются все оптимальные разбиения поставленной задачи кластеризации, то можно выяснить, какие объекты всегда входят в одни и те же кластеры, образуя своеобразные «ядра» кластеров, а какие объекты в различных разбиениях «мигрируют» из класса в класс. Такая информация полезна для дальнейшей выработки классифицирующих правил. Однако, ввиду высокой размерности данных не всегда удаётся получить даже одно точное решение задачи кластеризации (оптимальное разбиение), поскольку для поиска решения применяются приближённые алгоритмы (алгоритмы локального поиска).

Для выявления множества объектов, формирующих «ядра» кластеров, можно рассмотреть два варианта: первый позволяет делать выводы о «ядрах» кластеров на основе анализа одного единственного решения, второй связан с поиском всех решений задачи.

Применение первого варианта показано на следующем примере.

Пример 7. Пусть в примере 5 известно одно из оптимальных разбиений: Diam =3, 0 ₁=1, O 2 =2, O 3 =2, O 4 =1, O 5 =1.

Данное решение моделируется следующей смарт -таблицей C -типа:

Diam  O1  O2  O3   O4 O5

[ {3}    {1} {2} {2} {1} {1} ] .

Предлагаемый метод выявления «ядер» кластеров основывается на последовательной проверке отношения логического следования для каждой из компонент O i имеющегося решения в отдельности. Если компонента O i выводится из имеющихся посылок, то соответствующий объект принадлежит «ядру» определённого кластера; если отношение логического следования не выполняется, то объект является «мигрирующим». Выполнение отношения логического следования проверяется путём установления пустоты соответствующей смарт -таблицы с использованием утверждений 1-7 .

Как показано в примере 5 , при Diam =3 исходная система посылок позволяет сформировать следующее частичное присваивание:

O Diam O 1 O ₂ O 1 O ₃ O₂ O₄

[{1}    {3}     *      *       *], которое соответствует логическому выражению:

( O 1 =1) л ( Diam =3) л ( O 1 * O 2 ) л ( O 1 * O ₃) л ( O 2 * O 4 ).

Необходимо проверить, выполняется ли отношение выводимости для первой компоненты имеющегося решения ( O 1 =1). Для этого должно выполняться следующее логическое следование:

( 0 1 =1) л ( Diam =3) л ( 0 1 * O 2 ) л ( 0 1 * O з ) л ( O 2 * O 4 ) |= ( 0 1 =1).

На языке смарт -таблиц это означает, что должно соблюдаться соотношение:

O Diam O 1 O₂ O 1 O ₃ O₂ O₄   O 1 Diam O 1 O ₂ O 1 O ₃ O ₂ O ₄

[ {1}    {3}      *      *       * ] с [ {1}     *       *      *       * ] .

Смарт -таблица слева от знака с покомпонентно включена в смарт -таблицу, располагающуюся справа от этого знака. Это означает, что логическое следование выполняется, а объект O 1 входит в «ядро» кластера «1».

Для O 2 =2 требуется проверить справедливость следующего соотношения:

( 0 1 =1) л ( Diam =3) л ( 0 1 * O 2 ) л ( 0 1 * O з ) л ( O 2 * O 4 ) |= ( O 2 =2).

Известно, что установление логического следования A |= B равносильно установлению противоречивости формулы A л— B [20] .

Тогда для компоненты O ₂=2 необходимо выяснить противоречивость формулы:

( 0 1 =1) л ( O 2 = 1) л ( 0 1 * O 2 ) л ( 0 1 * O з ) л ( O 2 * O 4 )

или, что равносильно, требуется выяснить, пуста ли следующая смарт -таблица C -типа:

O 1 O₂ Diam O 1 O₂ 0 1 0 3 O₂ O₄

[ (1} {1}    {3}      *       *       * ] ■

Получается противоречие, объекты O 1 и O ₂ не могут одновременно попадать в первый кластер, так как O 1 * O ₂. Проверка для объекта O ₃ происходит в точности, как и для O ₂. Также получается противоречие.

Теперь проверяется компонента O ₄: ( O 1 =1) л ( O 1 * O ₂) л ( O 1 * O ₃) л ( O ₂ * O ₄) |= ( O ₄=1).

Смарт -таблица

O 1   O₄ Diam O 1 O ₂ 0 1 0 3 O₂ 0 ₄

[ {1} {2}    {3}      *      *       * ]

также пуста. Этот вывод сделан согласно утверждениям 6 и 7 на основе следующих рассуждений: анализируя ( 0 1 =1) и ( 0 1 * 0 ₂), получается, что 0 ₂=2. Далее, анализируя ( 0 ₂=2) и ( 0 ₄=2) и ( O 2 * O 4 ), выявляется противоречие.

Таким образом, объекты 0 1 - 0 ₄ формируют «ядро» соответствующих кластеров и не могут мигрировать.

Осталось проверить последнюю компоненту вектора решений 0 ₅=1: ( 0 1 =1) л ( 0 1 *0 2 ) л ( 0 1 * 0 3 ) л ( 0 2 * 0 4 ) h ( 0 5 =1).

Для формулы ( 0 1 =1) л ( 0 ₅=2) л ( 0 1 * 0 ₂) л ( 0 1 * 0 ₃) л ( 0 ₂ * 0 ₄) можно подобрать следующую выполняющую подстановку 0 1 =1, 0 ₂=2, 0 ₃=2, 0 ₄=1, 0 ₅=2. Таким образом, логическое следование для O 5 не выполняется, объект O 5 может попадать как в первый, так и во второй кластеры, т.е. лежит на границе кластеров.

Таким образом, можно сделать вывод, что «ядро» кластера «1» составляют объекты O 1 ,

O ₄, «ядро» кластера «2» - объекты O ₂, O ₃. Объект O 5 является «мигрирующим».

Второй способ выявления множества объектов, формирующих «ядра» кластеров, сводится к анализу всех полученных оптимальных разбиений. Для этого составляется таблица разбиений объектов по кластерам на основании двух полученных решений (см. таблицу 2).

Таблица 2 - Разбиение объектов на кластеры на основании двух решений

Объекты	Кластеры
0 1	1
0 2	2
0 3	2
0 4	1
0 5	1, 2

Из такого представления видно, какие объекты при любом разбиении попадают в один кластер и формируют его «ядро», а какие «мигрируют».

Заключение

При решении практически значимых задач интеллектуального анализа данных поиск глобального оптимума сильно затруднён большими объёмами обучающих выборок. Для снижения остроты данной проблемы предлагается использовать современные технологии ускорения комбинаторного поиска, позволяющие учитывать и анализировать разнородные экспертные знания о ПрО с целью раннего исключения заведомо неперспективных альтернатив, что обеспечивает пошаговую редукцию пространства поиска. Анализ знаний о ПрО обычно существенно упрощает решение задач комбинаторного поиска, к которым относится и рассматриваемая задача кластеризации с частичным привлечением учителя. Как правило, подобные задачи кластеризации решаются путём модификации известных методов локального поиска, при этом находится хотя бы одно решение задачи, причём не гарантировано, что оптимальное [21].

В работе описан подход к систематическому поиску глобального оптимума в рассматриваемых задачах кластеризации в рамках парадигмы программирования в ограничениях. Задачу кластеризации с частичным привлечением учителя предложено решать как задачу удовлетворения ограничений. Для моделирования основных и ряда дополнительных условий используются специализированные табличные ограничения - смарт -таблицы D -типа. При этом, введение дополнительных ограничений не только не замедляет вычислений, но и способствует выполнению более глубокой редукции пространства поиска.

При использовании предлагаемого подхода на основе анализа одного из оптимальных решений задачи может быть сделан вывод о том, какие объекты лежат на границе кластеров, а какие принадлежат одному и тому же кластеру при любом оптимальном разбиении. Данный анализ опирается на теоретико-множественную трактовку отношения логического следования P ( x ) ^ Q ( x ) и выполняется путём вычисления алгебраических выражений со смарт -таблицами, моделирующими области истинности M P и M q предикатов P ( x ) и Q ( x ), соответственно.

Представленные исследования выполнены в рамках темы НИР «Разработка теоретических и организационно-технических основ информационной поддержки управления жизнеспособностью региональных критических инфраструктур Арктической зоны Российской Федерации». При исследовании критических инфраструктур, к числу которых относятся транспортная, топливная, инфраструктура многих промышленных предприятий, особую важность приобретают методы объяснимого (интерпретируемого) искусственного интеллекта, ввиду слишком высокой цены ошибки при принятии управленческих решений. Важной задачей в процессе управления критическими инфраструктурами является определение областей «родственных» состояний, в пределах которых объект управления ведёт себя примерно одинаково, несмотря на некоторые различия в значениях параметров. С этой задачей тесно связана задача выявления условий значимого изменения состояния, приводящего к изменению пове- дения объекта управления. В качестве инструмента решения упомянутых задач предложено использовать авторские методы кластеризации, которые позволяют выявлять глобальный оптимум и определять «ядра» кластеров, т.е. множество объектов при любом оптимальном разбиении принадлежащих определённому кластеру.

Часто решение задачи кластеризации предшествует решению задачи классификации. На основе анализа «ядер» кластеров появляется возможность генерировать более качественные правила классификации, чем на основе некоторого одного разбиения, обеспечивающего локальный оптимум. Разработанный метод кластеризации представляется эффективным инструментом подготовки информации, необходимой для извлечения из больших наборов данных причинно-следственных зависимостей между регистрируемыми событиями, возникающими в процессе управления безопасностью и жизнеспособностью критических инфраструктур. Повышение качества выявленных причинно-следственных связей способствует повышению оперативности выработки управляющих воздействий, что крайне важно при прогнозировании (предотвращении) и/или ликвидации негативных последствий внештатных ситуаций на объектах критических инфраструктур. Метод был успешно применён для определения зон участка горного массива с различным уровнем сейсмической активности, что позволило обеспечить требуемый уровень безопасности при проведении горных работ.