Кластерный анализ флуктуации проводимости тонких платиновых плёнок

Кластерный анализ - задача разбиения заданной выборки объектов (ситуаций) на подмножества, называемые кластерами, так, чтобы каждый кластер состоял из схожих объектов, а объекты разных кластеров существенно отличались [1]. Кластерный анализ - это многомерная статистическая процедура, выполняющая сбор данных, содержащих информацию о выборке объектов, и затем упорядочивающая объекты в сравнительно однородные группы (кластеры). Кластер -группа элементов, характеризуемых общим свойством, главная цель кластерного анализа - нахождение групп схожих объектов в выборке.

Согласно представлениям фликкер-шумовой спектроскопии [2], реальный случайный процесс является суммой процессов, различных по своей природе. Можно выделить «ламинарную» фазу, когда процесс стационарный и не содержит нерегулярностей (всплесков и скачков). Иногда «ламинарная» фаза перемежается с «турбулентной», которая характеризуется существенной не-стационарностью. Кроме того, в любом случайном процессе могут присутствовать выбросы и скачки. Применение кластерного анализа позволяет разделить эти процессы. Это необходимо для того, чтобы проанализировать их причину и описать закономерности появления нерегулярностей.

Описание эксперимента

Цель эксперимента состояла в том, чтобы определить характеристики флуктуаций проводимости терморезисторов 701-102ВАВ-ВОО, представляющих собой тонкие платиновые плёнки в форме меандра, нанесённые на подложки. Дня сравнения одновременно регистрировались флуктуации проводимости магнитного детектора HMC1021Z, представляющего собой пермаллоевую плёнку в форме меандра, а также прецизионные непроволочные резисторы С2-14.

Исследуемые сенсоры были включены в мостовую схему, на которую подавалось постоянное напряжение U_m. Всего было собрано 6 мостов: 4 моста с платиновыми резисторами (Pt( 1 )-Pt(4)) по 2 в каждом, которые были соединены в полумосты, 1 мост - с магнитным детектором, 2 пермаллоевых резистора которого были также соединены в полумост, 1 мост с прецизионными резисторами для регистрации «фона» флуктуаций. Другие сопротивления всех этих мостов были такими же прецизионными резисторами номиналом 1 кОм. Магнитный детектор и платиновые терморезисторы имели номинал также около 1 кОм. Напряжение в диагонали каждого моста усиливалось с помощью операционного усилителя (ОУ) AD623. Как мосты, так и ОУ запитывались от одного аккумулятора с напряжением U_p = 12 В. Выходные напряжения из усилителей подавались на входы 16-канальной платы сбора данных L-1450 для одновременной регистрации флуктуаций. Частота регистрации составляла f_max = 13,9 Гц для каждого из шести каналов. Длительность регистрации составила 17 дней.

Обработка результатов

Все данные были разбиты на записи с половинным перекрытием по времени. Длительность одной записи Т= 589 с. Количество записей У составило 4080.

Существует бесконечное множество видов кластеризаций. Наиболее удобной является кластеризация в двумерном пространстве выбранных параметров.

Первый способ кластеризации.

1. Обезразмеривание: U (/) =

£(0 ит

’ где ^ит

- напряжение моста.

• 2.    Вычитание линейного сплайна.

• 3.    Вычитание выбросов.

• 4.    Быстрое Фурье-преобразование. Получаем [/*(/).

• 5.    Определение спектра мощности флуктуаций 8 (/) = -———— .

• 6.    Определение параметра у методом наименьших квадратов путём приближения степенной функцией S(f )~ a] f^Y без учёта низших частот.

• 7.    Другой безразмерный параметр Р характеризует мощность флуктуаций в выбранном диа-

• 1 т 2

пазоне частот: Р = — j|(7(?)| dt.

о

Для кластеризации были выбраны 2 безразмерных параметра: Р и у . Параметр Р является характеристикой энергии флуктуаций проводимости, а у является их спектральной характеристикой. Для белого шума у = 0, для стационарного фликкер-шума у = 0,8-1,2, а для нестационарных процессов у >1,5 [3]. Фликкер-шум обусловлен преимущественно внутренними процессами, происходящими в металлической плёнке, например, флуктуациями подвижности носителей заряда. Нестационарные процессы обусловлены, в основном, внешними воздействиями, например, флуктуациями электромагнитного поля, тепловыми потоками или воздействием скрытой материи. Если изобразить каждое измерение точкой на графике Р-у , то они группируются вокруг определённых центров. Информацию о флуктуациях проводимости образцов несёт количество кластеров, их положение и форма. В звёздной астрономии аналогом является диаграмма «спектр-светимость». Звёзды на этой диаграмме располагаются не случайно, а образуют хорошо различимые кластеры.

Результаты обработки флуктуаций проводимости для шести образцов представлены на рис. 1. Заметно существенное сходство форм и положений кластеров для всех образцов с платиновыми терморезисторами. Большая часть точек попадает в кластер, который можно охарактеризовать как стационарный фликкер-шум. Заметен также кластер белого шума у всех четырёх образцов Pt(l)-Pt(4). Нестационарный шум не образует отдельного кластера, а является продолжением основного фликкер-шумового кластера. Диаграммы двух других образцов существенно отличаются от первых четырёх. Образец с прецизионными резисторами был использован, чтобы оценить шумы от них самих и шумы усилительного тракта. Эти флуктуации образуют компактный кластер на диаграмме Р-у . Подобный кластер можно заметить на всех остальных диаграммах, особенно на диаграмме Pt(3), Pt(4) и у магнитного детектора.

Таким образом, этот метод кластеризации позволяет отделить различные виды шумов друг от друга, чтобы исследовать их закономерность. Кроме того, наличие существенного сходства кластеров, полученных от аналогичных источников, и значительные отличия их от других позволяют создать алгоритм идентификации образцов по их шумовым характеристикам.

Предложим другой способ обработки того же статистического материала.

• 1.    Определение спектра мощности флуктуаций S^f^ (повторение пп. 1-5 из первого способа).

• 2.    Вычитание линейного сплайна 8° (/) = S^f^-^k • f + а), полученного методом наимень

• 3.    Определение максимума функции 5° = maxes'⁰ (/)j по всему исследуемому частотному диапазону, исключая низкие частоты и соответствующую ему частоту f_m.

• 4.    Нормировка S^ = S^Jog , где cr_s - стандартное отклонение функции 8° (/).

• 5.    Построение графика зависимости 5_тах (/_т) (рис. 2, 3).

ших квадратов.

Этот способ позволяет выявить резонансные частоты в спектре флуктуаций. Для сравнения построим усреднённые спектрограммы флуктуаций (S') как функции частоты / На диаграммах слева явно выделяются резонансные частоты, а на графиках справа они видны гораздо слабее или совсем не видны, например у образца Pt(3). Резонансные частоты флуктуаций проводимости, вероятно, связаны с внешними воздействиями. У образцов с платиновыми терморезисторами они составляют: 2,05, 2,13, 2,21, 3,08, 3,36, 4,24, 5,28, 5,64, 6,31, 6,38, 6,46 Гц. У образца с магнитным датчиком: 1,67, 1,82, 2,13, 2,33, 2,79, 3,87, 4,00, 4,26, 4,67, 5,00, 5,35, 6,00, 6,67 Гц. Совпадающие или близкие частоты выделены полужирным шрифтом. У образца с прецизионными резисторами резонансных частот не обнаружено.

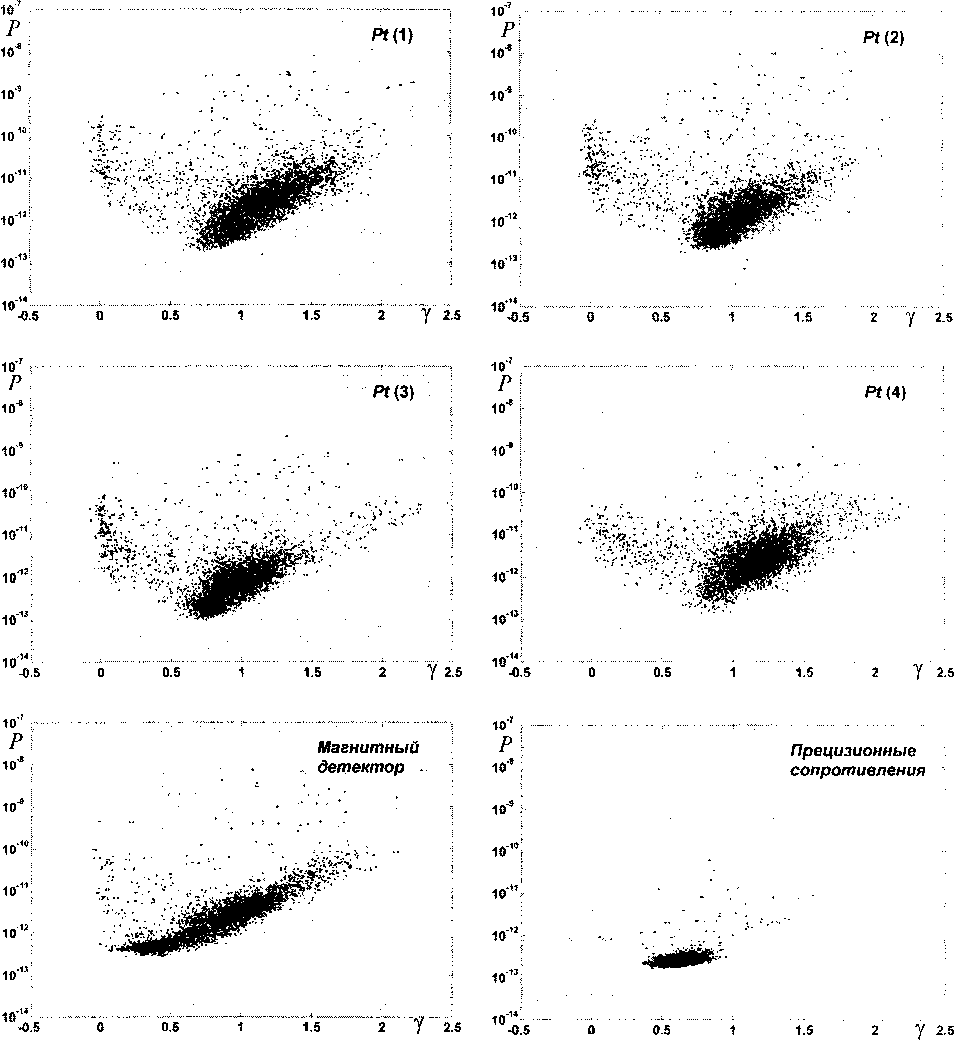
Рис. 1. Кластеры флуктуаций проводимости образцов платины (Pt(1)—Pt(4)), а также магнитного детектора и прецизионных сопротивлений в координатах Р-у

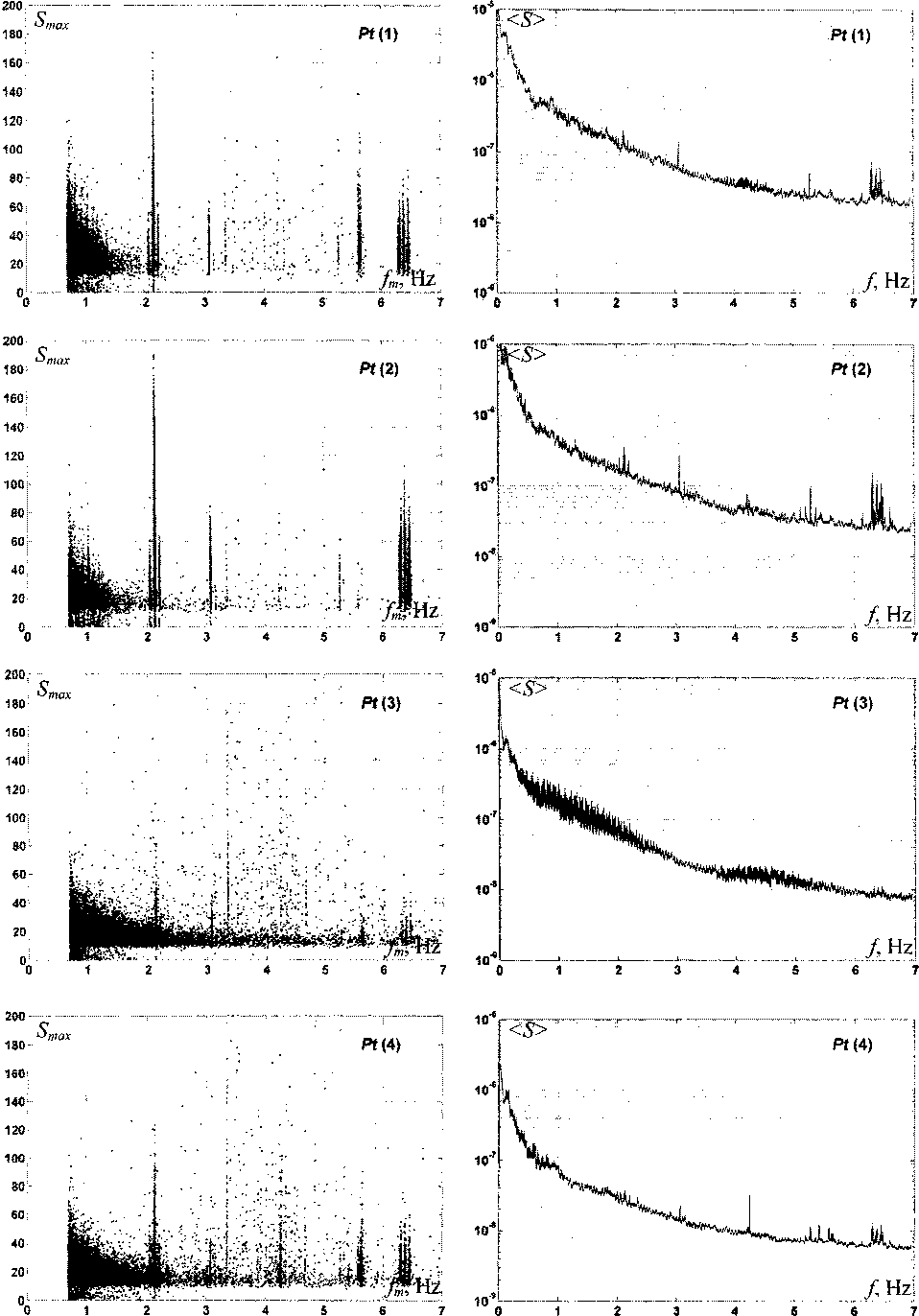
Рис. 2. Кластеры флуктуаций проводимости образцов платины (Pt(1)-Pt(4)) в координатах £„„-/„ (слева) и усреднённые спектрограммы (справа)

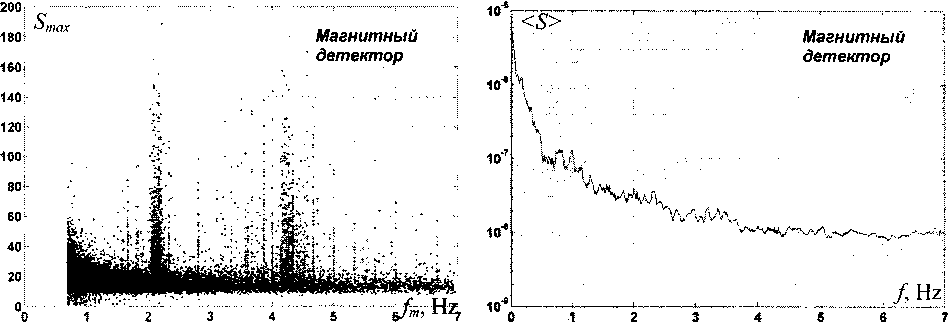
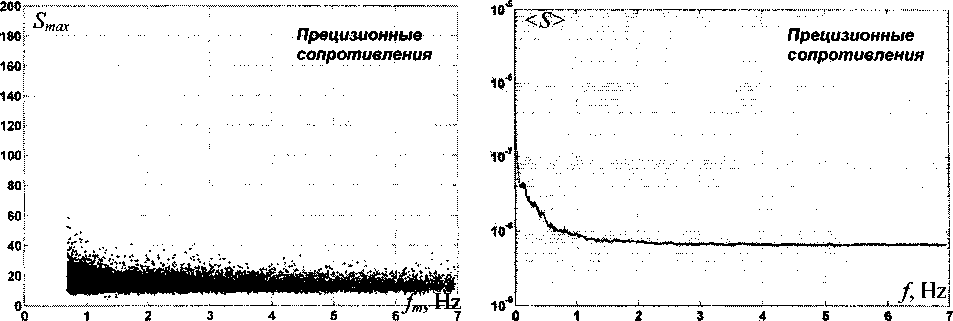
Рис. 3. Кластеры флуктуаций проводимости магнитного детектора и прецизионных сопротивлений в координатах S_m„~f_m (слева) и усреднённые спектрограммы (справа)

Таким образом, этот метод кластеризации позволяет выявить внешние периодические воздействия на детекторы и особенности их отклика на них.