Коэффициент Зеебека смеси электролитов гидроксида натрия-йодида калия

Возникновение термоэлектрической ЭДС в растворах водных электролитов было открыто достаточно давно. Микроскопический механизм возникновения разности электрических потенциалов в растворе электролита, находящегося в неоднородном температурном поле, может быть объяснен в рамках термодинамики необратимых процессов.

Ключевую роль в данном явлении играет термодиффузия. Под действием градиента температуры в жидкой смеси электролита возникают потоки заряженных частиц, катионов и анионов, направленные

N

Fgrad (ф)=^т к к=2

справедливое в случае электрически разомкнутой цепи (отсутствия электрического тока). В данном выражении F - постоянная Фарадея, ф - электрический потенциал, N - количество заряженных частиц в системе, т_к - приведенное число переноса частиц вида k , p_k - их электрохимический потенциал, T, P - температура и давление

^{- (} grad ^ k Т,

— Q^gradT

против градиента температуры. Вследствие неравноценности данных потоков внутри электролита практически сразу же возникает электрическое поле при создании градиента температуры. В дальнейшем в электролите формируется градиент концентрации, который приводит к дополнительному вкладу в величину термоэлектрической разности потенциалов. Применение законов термодинамики необратимых процессов к данному явлению позволяет получить выражение для итоговой величины термоэлектрической разности потенциалов [1].

соответственно, Qk - величины, называемые теплотой переноса k-х ионов. Особенно простое выражение для градиента термоэлектрической разности потенциалов получается в случае единственного электролита, распадающегося на два вида противоположно заряженных частиц grad(ф)=  / 2  1

F ⁽ z + ^a + -

— 2  1

+ z_a_ ) _

z + ^a +

(- RTgrad ( ln ( x )) - ^Q + grad ( T ) ^

+

+

( z - a -

V

RTgrad ( in ( x ))

QF grad ⁽T )

T          7

Здесь градиенты электрохимического потенциала заменены на градиенты молярности x ионов, R – универсальная газовая постоянная, феноменологические ко- эффициенты a± - выражаются через объемные концентрации и подвижности ионов u a+

c + u +

Fz + ’

a

cu

Fz

Первые слагаемые в квадратных скобках обусловлены формирующимися в электролите, на который наложена температурная неоднородность, градиентами концентрации заряженных частиц, вторые слагаемые пропорциональны градиентам температуры. Вследствие того что коэффициенты диффузии в водных растворах электролитов на несколько порядков ниже коэффициентов теплопроводности [1], стационарное неоднородное распределение концентраций в электролите формиру- ется значительно позже формирования стационарного распределения температуры. Поэтому для так называемого началь- ного состояния, справедливого для на- чальных моментов времени первыми слагаемыми в формулах (1), (2) можно пренебречь. Тогда коэффициент термоэлек- трической ЭДС a = ^^ для простого би- нарного электролита

a =

F ( z 2 a ₊ + z.

_ a_ )

za

+

Q +

T

za

Q -

T

.

Как видно из последнего выражения знак и величина коэффициента Зеебека такого электролита определяется соотношением между теплотой переноса Q и подвижностью u анионов и катионов.

Ранее были проведены многочисленные исследования явления Зеебека в таких простых системах [2]. Данные эксперименты совместно с экспериментами по измерению коэффициента термодиффузии в частности позволили определить величины теплоты переноса различных ионов. С другой стороны большинство распространенных в окружающей природе жидких электролитов являются смесями различных веществ. Например, биологические жидкости живых организмов: кровь, лимфа и т.д. Жидкие смесив в таких системах, находятся, как правило, в неравновесных условиях, в них существуют градиенты температуры. Поэтому в таких системах будут формироваться термоэлектрические разности потенциалов, которые могут играть важную роль. Так в работе [3] было показано, что медицинский раствор Рингера, моделирующий ионную составляющую человеческой крови, обладает необычными термоэлектрическими свойствами, которые могут отвечать за включение механизмов терморегуляции живых организмов. Раствор Рингера, как раз, представляет собой смесь неорганических солей в воде. Поэтому исследование термоэлектрических свойств таких жидких смесей представляет собой актуальную задачу.

В нашей работе исследуются термоэлектрические свойства водной смеси NaOH+KI. Величина термоэлектрической ЭДС растворов электролитов измеряется с помощью экспериментальной установки описанной в работе [4]. Концентрация гидроксида натрия в смеси была фиксированной и равной 0.9 г/л.

На рисунке 1 представлена зависимость разности термоэлектрических потенциалов в водном растворе NaOH указанной концентрации. Коэффициент термоэлектрической ЭДС данного раствора может быть определен из линейной аппроксимации экспериментальных данных. Он составляет α = -618 мкВ/К. Отрицательный знак коэффициента обусловлен тем, что под- 2 эксперимент линейная аппроксимация 0 -2 Е . -4 -6 -8 -2    0    2    4    6    8    10   12   14   16 AT. K

вижность анионов OH- значительно выше катионов Na+[5]. Теплота переноса гидроксид ионов также превышает аналогичную для ионов натрия. Кроме того экспериментальная линейная зависимость для разности электрических потенциалов качественно согласуется с теоретической формулой (5) справедливой для начального состояния. 2,3 2,2 эксперимент линейная аппроксимация 2,0 1,9 1,8 1,7 1,6 20       25       30       35       40 Δ T, K

1. Зависимость термоэлектрической

Рис.

,

разности потенциалов Δφ, от разности температур ΔТ в водном растворе NaOH концентрацией 0.9 г/кг

Рядом на рис. 2 представлена аналогичная зависимость для раствора KI концентрацией 0.1 г/л. Коэффициент термоЭДС данного раствора составляет -29 мкВ/К, что на порядок ниже, чем для NaOH. Данный результат обусловлен малым различи-

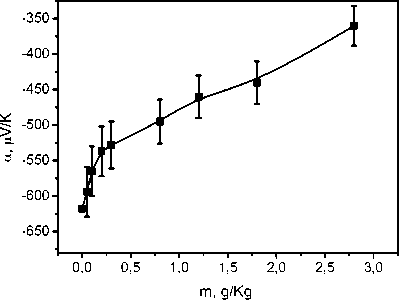
Рис. 3. Зависимость коэффициента тер-моЭДС раствора, содержащего 0,9 г/кг

NaOH от содержания KI.

На рисунках 3, 4 представлены уже концентрационные зависимости коэффи-

Рис. 2. Зависимость термоэлектрической разности потенциалов Δφ, от разности температур ΔТ в водном растворе KI концентрацией 0.1 г/кг

ем в величинах подвижностей ионов K+,

u = 7,6 ⋅ 10

-

⁸ м²/В·с и  I^-,    u

= 8,0 ⋅ 10 ^{- 8},

данные приведены для бесконечного разбавления [5].

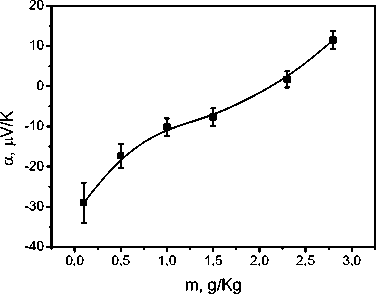
Рис. 4/ Зависимость коэффициента тер-моЭДС, беспримесного раствора KI, от содержания KI.

циента термоЭДС для смеси с фиксированной концентрацией гидроксида натрия

и переменном значении концентрации йодистого калия и для беспримесного раствора йодистого калия. В случае смеси двух веществ коэффициент термоэлектрической ЭДС уменьшается по абсолютной величине до -355 мкВ/К для смеси NaOH (m = 0,9 г/кг) и KI (m = 2,8 г/кг). Данное уменьшение качественно согласуется с уменьшением термоэлектрической ЭДС беспримесного раствора KI. При этом если в области низких концентраций коэффициент термоЭДС данного раствора отрицателен по знаку, в области же высоких концентраций m > 2,3 г/кг он меняет знак. Также на основе результатов можно сде- лать вывод, что коэффициент термоЭДС исследуемой смеси в основном определяется вкладом вещества, имеющего большее значение коэффициента термоЭДС т.е, NaOH. Данный вывод согласуется с соотношением (1). При этом следует отметить, что масштабы изменения коэффициента термоЭДС существенно отличаются для исследуемых растворов. Если в смеси двух веществ коэффициент термоЭДС при изменении концентрации KI изменяется на 300 мкВ/К, то в беспримесном йодистом калии при аналогичном изменении концентрации KI коэффициент меняется на 40 мкВ/К.