Колебания крыла самолета в условиях, связанных с разным коэффициентом демпфирования

Актуальность статьи обусловлена отсутствием комплексного и исчерпывающего источника информации по влиянию коэффициентов демпфирования на характеристики полёта самолёта. Настоящие исследования фокусируются на отдельных аспектах демпфирования, либо на специфических условиях колебаний, но не дают полного набора данных. Опубликованные работы и учебники сосредоточены не обеспечивают целостного подхода к пониманию взаимодействия различных видов демпфирования и их влияния на колебания крыла. В то время как авиационная техника и требования к безопасности и эффективности полета стремительно развиваются, возникает необходимость в систематизированных данных и анализе, способном интегрировать информацию о разных коэффициентах демпфирования в одном исследовании. Для решения данной проблемы предназначена эта работа.

Как известно, из линейной и нелинейной аэродинамики самолётов, коэффициенты демпфирования отражают способность тела снижать амплитуду колебаний за счёт уменьшения энергии. Существуют следующие типы коэффициентов демпфирования:

• -    коэффициент вязкого демпфирования (viscous damping coefficient) –связано с сопро-

• тивлением, возникающим при взаимодействии крыла и воздушных потоков [1, 2];

• -    коэффициент структурного демпфирования (structural damping coefficient) – учитывает потери энергии внутри материалов конструкции крыла, особенно композиционной структуры, из-за внутренних трений и микроскопических деформаций [2];

• -    коэффициент аэродинамического демпфирования (aerodynamic damping coefficient) – зависит от скорости воздушного потока и формы крыла, а также от его угловых перемещений и деформаций [3];

• -    коэффициент магнитореологического демпфирования (magneto-rheological damping coefficient) – регулируется магнитным полем и используется в активных демпфирующих устройствах, которые могут изменять жесткость и демпфирующие свойства в реальном времени, применяется для активного контроля колебаний крыла [4];

• -    коэффициент кулоновского демпфирования (Coulomb or dry friction damping coefficient) – вызвана силами трения между соприкасающимися поверхностями, что характерно для соединений и узлов, например, шарниров или подвескок [1];

• -    нелинейное демпфирование (nonlinear damping coefficient) – зависит от амплитуды и

• скорости колебаний, учитывает угловые деформации, часто встречается при анализе флаттера и больших амплитудных колебаний [5].

В большинстве моделируемых системах полёта самолётов используются лишь коэффициенты вязкого и аэродинамического демпфирования, так как учёт всех эффектов приводит к чрезвычайно сложным расчётам, из-за чего часто прибегают к экспериментам. Рассмотрим простейшую ситуацию.

Пусть за основное, опорное, движение самолёта примем горизонтальный установившийся полёт и рассмотрим короткопериодическое свободное возмущённое движение, которое описывается дифференциальным уравнением [6]:

Ай + 2hkAa + wk — 0,                               (1)

где a - угол между подъёмной силой и горизонтальной осью, hk - коэффициент демпфирования, шк - опорная частота или частота недемпфированных колебаний. Для решения уравнения (1) составим характеристическое уравнение:

Л2 + 2hkЛ + шк — 0,

Решая которое, как квадратн ое уравн ение, находим, что Л 1, ₂ — —h k ± ± ²^ ² +шк . Далее рассмотрим два случая. Если h k ² >  Ш , то решение действительно и представимо в виде Аа — С 1 е ^{Л 1 С} + C₂e ^^{2 t} - движение апериодическое, постоянные С находятся из начальных условий. Если hk²< Ш , то корни уравнения станут Л₁₂ — h k + i ^шк- h^, а решение будет колебательным и примет вид Аа —

Ае hkt sin (J^k — hk2 • t + ^), где ные А и ^ находятся из начальных постоян-

условий.

Зная h k и ш к , а также начальные условия, можно найти вид решения Аа, а после - ско-

рость изменения угла наклона траектории и перегрузку.

В начале вращательного возмущения опорного движения преобладает короткопериодическое движение, которое связано с нарушением равновесия моментов самолёта. При совершении манёвров в вертикальной плоскости и устоявшемся движении можно определить динамические характеристики устойчивости и управляемости, зная h k и Ш к , например, период собственных колебаний самолёта Т к —

2nT

:, время затухания колебаний t

^ ^1- h_k^{2 /} M_k

3Т      -           _ h 2!^, заброс угла атаки

-exp (

fi-bk2/^

ъКк/ы ь

Если движение лишь вращательное, то hk^m^ + m?), но также оно зависит от т“, и m^z, которые обусловлены нестационарным движением несущей поверхности, а также от интерференционных слагаемых этих величин. Известно [3], что основной вклад в значение величины hk вносит горизонтальное оперение, угол стреловидности крыла на дозвуковых и малых сверхзвуковых скоростях полета на демпфирующие характеристики самолета существенного влияния не оказывает, а также то, что роль интерференционной составляющей в суммарном hk самолета заметна только на дозвуковой скорости.

В одном из исследований [7] проводилось сравнение теоретически рассчитанных параметров полёта и экспериментальные значения. На рисунке 1 представлено графическое сравнение кривых значений приведённых коэффициентов демпфирования крена С^ и рыска ^{нья С} п_г ^[7]

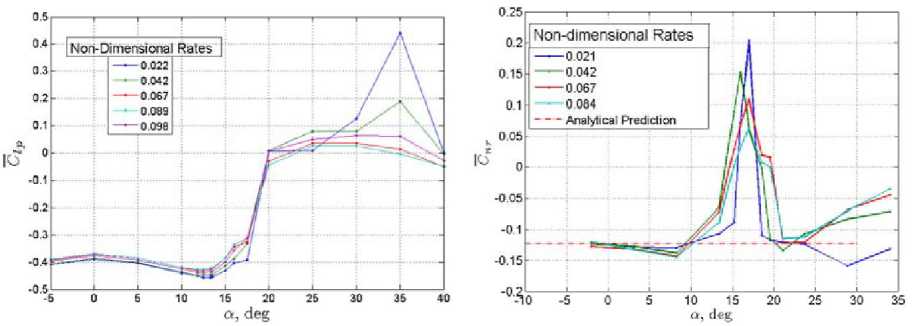
Рис. 1. Зависимости C i и С_Пг от угла атаки при различных величинах собственных частот (безразмерных)

Показано, что в экспериментальные значения отличаются от теоретических только в области срыва, но согласуются в предсвалной области.

Можно сделать заключение, на основе приведённых данных, что исследование колебаний крыла самолета при различных коэффициентах демпфирования имеет большое значение для повышения устойчивости авиационных конструкций, особенно с учётом то- щиеся значения от теоретически предсказанных величин. Взаимосвязи между аэродинамическими, структурными, вязким и другими коэффициенты, возможно, могут иметь большое значение, особенно при высоких нагрузках и манёврах. Для описания динамики самолётов необходимо прибегать к дифференциальному исчислению, уравнения становятся сложнее, что необходимо учитывать при моделировании реальных полётов.

го, что эксперименты показывают отличаю-