Колебания неоднородного пороупругого слоя с пустыми порами

Введение. Теория пористых линейно упругих материалов с пустотами первоначально была разработана Коуином и Нунциато [1]. Она предназначена для моделирования упругих материалов, содержащих распределение малых пор (рис. 1). Главной особенностью данной теории является введение в определяющие соотношения новой переменной, характеризующей относительный объём пор, который берётся в качестве независимой кинематической переменной. Включение новой переменной требует дополнительных сил для обеспечения равновесия объёма пор. Если объём пор обращается в ноль, поведение материала описывается классической теорией упругости.

Теория Коуина—Нунциато хорошо описывает поведение композитных, керамических, пенистых и пористых материалов. При этом ряд функционально-градиентных материалов отличается тем, что распределение физических характеристик неравномерно, что приводит к их зависимости от координат.

Настоящая работа посвящена исследованию колебаний неоднородного по толщине пороупругого слоя с пустыми порами.

1 Работа выполнена в рамках инициативной НИР.

Постановка задачи. Рассмотрим двумерную задачу об установившихся колебаниях с частотой Q неоднородного изотропного пористого упругого слоя 0 < у< /?, |х| < оо. Нижняя грань слоя горизонтальна и сцеплена с абсолютно жёстким основанием.

Необходимо найти поля перемещений в слое u (x,y^ = '_xu,v'_te ^m и функцию относительного объёма Ф(х,у,Г) = Ф(х,у)е^ при известных законах неоднородности под действием нагрузок, приложенных к верхней границе слоя.

Считая режим колебаний установившимся, отделим временной множитель е ^!Qt . Будем рассматривать амплитудные значения функций.

Уравнения движения имеют вид [2]:

о

+ ох/ / +pfi2u = 0, + о//к +рП2и = 0.

Компоненты тензора напряжений находятся из следующих определяющих соотношений [2]:

=   +(1-2с2)и' + НФ,

Л + 2р у v ’ у

-^- = (1-2сЧи'х +и' + НФ, о =ц(и' +и' L где Н=—^—, 1-2с2 = ——

Л + 2р          Л + 2р

Полевые характеристики задачи должны быть подчинены следующему уравнению [2]:

д2Ф а2Ф /шЮ + p/rQ2 - 5

Эх2 5у2

а

_ 9и 9v] _

Ф-- — + — = 0.

О ( 9х 9у )

Соответствующие граничные условия для слоя могут быть записаны в виде:

и (х,0) = 0.

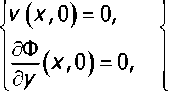
—(х,Л) = 0, 9у^у

где Л = Л(у), р = р(у) — положительные функции координаты у, являющиеся аналогами параметров Ляме, р — массовая плотность материала; о, Р, 5, со, к — положительные физические параметры, связанные с пористостью [1].

Система интегральных уравнений Фредгольма 2 рода. Отметим, что в представленной постановке колебания описываются системой уравнений в частных производных второго порядка с переменными коэффициентами. Наиболее эффективным средством анализа колебаний в слое является использование преобразования Фурье по переменной хи сведение к системам обыкновенных дифференциальных уравнений с переменными коэффициентами [3].

Функция называется прямым преобразованием Фурье f(x). В свою очередь, функция

1 00

fM=^J/r(s)e^s называется обратным преобразованием Фурье и с физической точки зрения это выражение представляет собой интегральную запись принципа суперпозиции гармоник с комплексной амплитудой и волновым числом sc непрерывным спектром.

Системы (1), (2) и уравнение (3) в образах Фурье выглядят следующим образом:

d          i

-•^saxx ⁺ -3-°XV ⁺ P^Q 0 = 0, dy ^y

~ d ~ ч

-■1SOxv^^W^^V-^

б

К

= —isd (А + 2p) + (1 - 2c² ) (Л + 2p) Д-v + НФ (А + 2p),

= (1 - 2c²) (X + 2p) (-isA 0 + (X + 2p) Д-v + НФ (X + 2p), X           / X          / X / X          /                  X          /

б

( d - . Д d -    . -

= р -и-ISV =р — U -\AISV. {dy ) dy d2 т fлой + pAQ2 -5 2K pf б - . n

—-Ф + ---------- - s Ф - - — v -isu = 0.

dy V ° J ^QVdy )

Если из (5)—(7) выразить функции                                исключить а также dy у dy уу dy dy dy ввести —Ф = Ф, получается каноническая система обыкновенных дифференциальных уравнений dy

1-го порядка с переменными коэффициентами:

dy у/ dy уу

= is

А

6 - pQ A + 2p yy P

= is6_xy - рй²й,

d - 1 ~      . ~

-U=-C + ISV, dy p y d -      1 ~      .

-;-v = ——a + is dy A + 2p ^yy

—Ф = Ф, dy

—ф =----а dy а(А + 2ц) yy

А + 2p

X - , -т-^-и-НФ, A + 2p

- 2/s - , \ 0 - а А + 2р

О + is2yHCD,

Aofi + pAQ²-^ ₂ ----------- - s + - H Ф.

а

а

Граничные условия в образах Фурье имеют вид:

t7(s,O) = O,

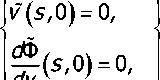
6_yy(s,A) = 6(s), ^($,А) = 0. vdy^{v 7}

Краевая задача для системы функций (8), (9) после введения безразмерных переменных и пара метров приведена к следующей безразмерной форме:

у did h' dy h dz

(ye[0,/7]^Ze[0,l])

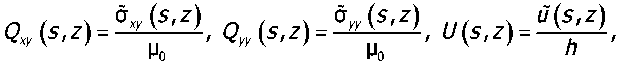
1/ (s,z) = ~^—^' Q($,^z) = O(s,z),

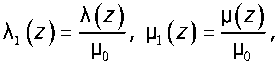
LI / P___________

1 Mo^l^ + ZM!^))

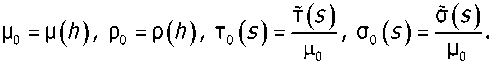
После замены для получения вещественных коэффициентов в вырожденной системе (со = 0)

iU=U_v iQ_xy=Q_v Q_W=Q„ она выглядит следующим образом:

(Ю)

^Qx=-hs-^-Q^ ^h^

dz A_t + 2p_t

k^V+Mj-pn^i Ai + 2M1 Mo

d „   , ~ рП²Л²..

= -J—5—Q + hs 7— 4-U_x - ^ф, dz K_x + 2p_t A_t + 2p_t

d

Tz^'

d         p/7²

--Ф = —----г dz o(A1+2p1)

Граничные условия:

Ux - "2.hs\\xHx($,

(И)

_ РЛ³             I , ₂ wfi + pAQ²-5       2 ДО и I

Q, - 2s -— , L U, - Л²------------ - h²s² + -— H. cp.

2 a A!+2p! 1 ( a                a J

'^(5,о) = 0,

■И($,0) = 0, ip(s,0) = 0.

В общем случае построение решения канонической системы дифференциальных уравнений (11) с переменными коэффициентами в аналитической форме невозможно, поэтому осуществляется её сведение к системе интегральных уравнений Фредгольма второго рода. Интегрируя систему (11), учитывая граничные условия (12) и осуществляя элементарные преобразования, получим систему уравнений Фредгольма 2 рода с непрерывными ядрами (отметим, что все неизвестные функции зависят от параметра преобразования Фурье):

С₂ = J (ед₂ (п) + G^U_Y (n) + 6₃Ф (n)) dn - ihsT₀ (1 - z) + а₀,

О

■ ц = -J (ед2 (п)+ед, (п)+с6ф (п)) dn + /тои/ (z), о ф = J (ед2 (п)+gbuy (п)+ед(п))^п,

G, = ^(z,_n), /=1„9.

Ядра системы имеют вид:

>2^2

G.

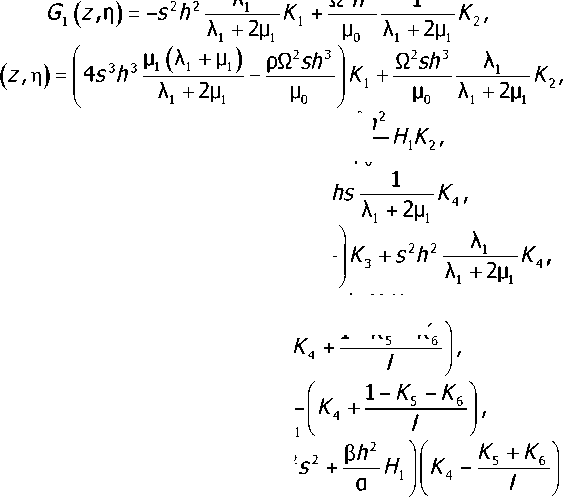
_ / x L ₂ ло^ + pAQ² ,₂ Gq (z,n) = - л ---------- - №

G₃(z,^ = -2s²h^_YH_YK_Y-^l Ио

^G^I ⁼ -^,K^^K=⁺' g₅ (z,n) = [ 45²л² М^±Ы _ 2^ ⁷ t ^Ai^+2|Ji m₀

G₆ (z,q) = -2hsy_YH_YK₃ - hsH_YK_A,

1 - К, - К

где

K, =K\z,x\Y /=1..6; \ =^(0), Mi =Mi(n), X'₁(z,n) = max{z,n}-z,

/C₂(z,n)= J pt/q, max{z,q} min{z,n} .

^(^П)= J -de,, 0 Pi

A'4(z,n) = z-min{z,n}, к5(^,п)= J g(^du, min{z,q} 1

^(^,0)= J g(^du, max{z,q}

^ + pAQ2 -5 ,2 2 P^2 и V g (q) = - Л2------------ - Л252 + -— HY pc,, v J              G                     G nV                                     /

2 юП + pAQ² - E

0 Mi

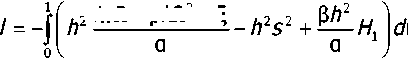
Численный метод решения системы интегральных уравнений и обращения преобразования Фурье. Осуществим дискретизацию системы интегральных уравнений Фредгольма 2 рода (13), используя квадратурную формулу трапеций [4, 5] и метод коллокаций. Придём к следующей алгебраической системе:

Дх = ——,   = st(i-1), / = 1,...,/7, л-1 v '

А=4,=^4 = 4=- = 4,-,=л*,

%, "ZA (^Gi,%,      ^{+ С}Л) = °« -ihsr^-^V            <¹⁴>

7=1

■ u_Xi +£4 ^+езД₅ +^7) = 7=1

Ф/ “ S A ^igQlj ⁺ ^ъд^\] ⁺ ^9дф; ) ⁼ О"

I 7=1

Значения остальных функций в соответствующих узловых точках Q^.V,,^, находятся из интегральных представлений:

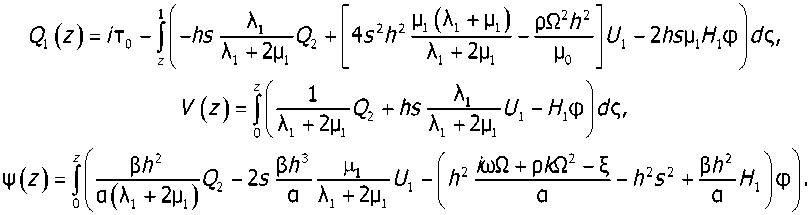
Таким образом, для любых значений параметра преобразования можно найти узловые значения переменных, и далее требуется построение обратного преобразования Фурье. Для численного осуществления обратного преобразования Фурье, т. е. для вычисления интеграла

• 1    ⁰⁰

используем интерполяционную формулу третьей степени, являющуюся аналогом «правила трёх восьмых» Ньютона-Котеса [5, 6]. Оно получается при замене функции F на каждом из отрезков [0,3^],[3^,6^],... алгебраическим многочленом третьей степени, интерполирующим F по четырём значениям.

Возьмём четыре точки                и выполним интерполирование F по её значениям в этих точках

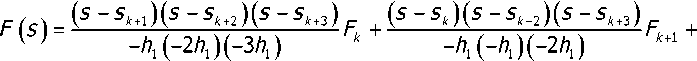
(с _ с Wc _ С Wc _ С 1

р ^kJV ^k’JV^{5 3}k+3) р

2A

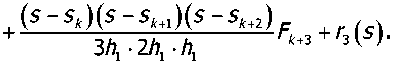
Умножение этого равенства на е ^lsx и интегрирование по отрезку [s^s^ +3^] с последующим суммированием по значениям к = 0,±3,±6,... приводит к представлению:

1 ™                 (v — /б ) ™                   + /б ) ™               я ™

• •         J ^Г VP ^Ub -            ^r3A+l^{e +}   ₇ 2_.^ГЗкА^{е + r}3k^{c +}₇ l^1DJ

  где

  

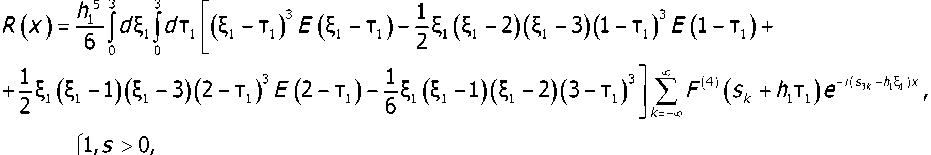
  E(s)4,s = 0,

  
  

Коэффициенты а3,у3,б3 имеют вид:

О = xh_v

h;x hy

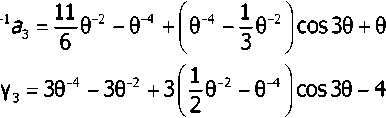
г3 sin 30

3 sin 30

/7^63 =59~3 + 3^0~2 -0 Jsin30 + 40 3COS30.

Стоит отметить, что численный эксперимент проводился для п = 30 узловых значений при точности е = 0,001.

Расчёт полей смещений и функции относительного объёма при некоторых законах неоднородности. В качестве примеров реализации предложенной схемы рассмотрим возрастающие и убывающие функции, характеризующие законы неоднородности в случае сосредоточенной и распределённой нагрузки.

Для сосредоточенной нагрузки находим:

о0 (х) = б(х); o0(s)= J б^е'^Фс = 1, т0 (х) = б(х); t0(s)= J ^e”xdx = l.

Для равномерно распределённой на отрезке нагрузки получим № = <>0, |х|<а.          sin (as)

Ь>М = 0, |х|>а '         ⁰ s '

т0(^) = т0, И ^5, то(х) = О, |х|>а '

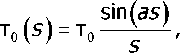
где а — полудлина области приложения нагрузки.

Будем рассматривать законы неоднородностей, для которых выполняются следующие ра венства:

jA₁(z)dz = l, Jp₁(z)dz=l, p(z) = 1, о                        о

Согласно физическому смыслу параметры Ляме должны удовлетворять условию

2(A1(z) + p1(z)) 2

Vz 6 [0;1]

Рассмотрим некоторый закон, удовлетворяющий условиям (16), (17) A1(z) = z + 0,5, p1(z) = l,5-z.

Пусть h =0,5; а = 0,01; Р = 10; со = 0,01; 5 = 15; к =0,01; Q = 100, а также

о0 GO = 1> to(s) = o.

Ниже приведены графики полей перемещения и функции относительного объёма. Сплошной ли нией обозначена действительная часть, пунктирной — мнимая часть.

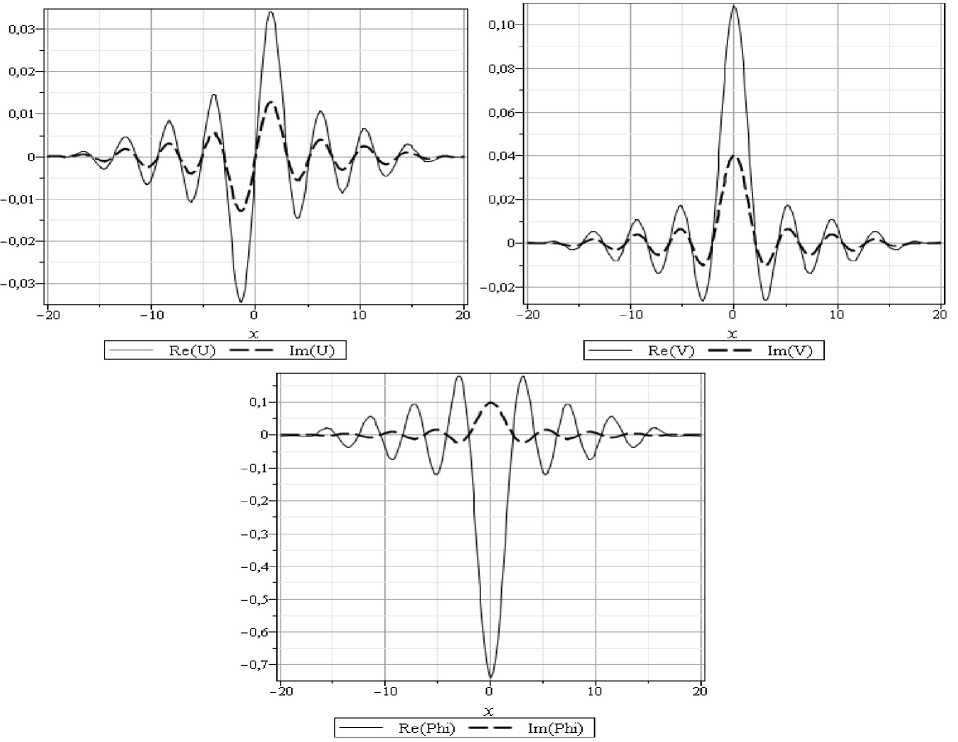
Рис. 2. Поля перемещений в слое и функция относительного объёма

Заключение. Разработан метод решения краевой задачи для неоднородного пороупругого слоя, позволяющий находить поля внутри и на поверхности для широкого класса неоднородностей.