Колебания звукопоглощающей перфорированной стеклопластиковой и углепластиковой панели с системой ячеек трубчатого типа

С середины ХХ в. широкое распространение получили многослойные конструкции, в большинстве это конструкции, выполненные из композиционных материалов.

В работе рассматривается звукопоглощающая панель, выполненная из полимерного композиционного материала - из стеклопластика и углепластика, которая состоит из двух слоев полых трубчатых элементов прямоугольного сечения. Данные конструкции применяются в авиационных двигателях и выполняют функцию звукопоглощения (рис. 1). Эти конструкции в процессе эксплуатации подвержены воздействию гармонических нагрузок как со стороны звуковой волны, так и со стороны конструктивных элементов, с которыми звукопоглощающие конструкции соединены. Источниками гармонических колебаний в турбореактивном двигателе являются [1]:

• -    турбулентное перемешивание скоростной струи газа с окружающим атмосферным воздухом;

• -    компрессор - взаимодействие роторов и статоров создает шум высокой частоты, как обычно сопровождается гармониками;

• -    газовая турбина;

• -    шумы сгорания, шумы турбины и компрессора.

Предлагается метод исследования динамического поведения звукопоглощающей панели из стеклопластика и углепластика, состоящей из двух слоев полых трубчатых элементов прямо- угольного сечения. Методом конечных элементов решается задача вынужденных колебаний стеклопластиковой и углепластиковой панелей, с учетом перфорации звукопоглощающей поверхности предложена прикладная методика оценки эффективности звукопоглощения на основе данных о спектре собственных частот композитной конструкции. Для представленных механических моделей звукопоглощающей перфорированной панели исследовано влияние перфорации несущего слоя на распределение частотного спектра и форм колебаний композитной конструкции.

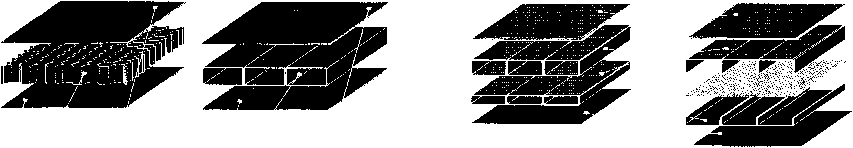
а                     б                       в                     г

Рис. 1. Звукопоглощающие панели: а – металлические; б – однослойные; в, г – двухслойные композиционные звукопоглощающие конструкции

Описание конструкции

Двухслойная звукопоглощающая панель представляет собой конструкцию, состоящую из двух рядов полых трубчатых ячеек, выполненных из композиционного материала и заключенных в оболочку (рис. 2). Панель имеет габариты: ширина – 138,5 мм, длина – 628,6 мм. В зависимости от конструкции авиационного двигателя, его агрегатов количество ячеек вдоль образующей, кривизна и метод крепления звукопоглощающей конструкции могут меняться.

Рис. 2 . Двухслойная звукопоглощающая панель. Вид с торца

Звукопоглощающая панель имеет две перфорированные поверхности – срединная и внутренняя. Процент перфорации внутренней поверхности составляет 6,3% (2575 отверстий диаметром 2 мм), а средней поверхности – 5% (2575 отверстий диаметром 1,6 мм).

Материал конструкции – стеклопластик на основе препрега ВПС-33, разработки ВИАМ, представляющего собой стеклоткань Т-10-14, пропитанную эпоксидным связующим ЭНФБ-2М. Физико-механические характеристики стеклотекстолита ВПС-33 представлены в работе [2].

Таким образом, звукопоглощающая панель представляет собой оболочечную конструкцию, усложненную звукопоглощающими полыми трубчатыми ячейками и композиционным материалом, из которого она изготовлена. Наличие перфорации срединной и внутренней поверхностей вносит дополнительную сложность в расчет конструкции.

Физическая постановка

Анализ гармонического воздействия используется для определения параметров установившегося движения линейной системы при синусоидальном силовом возбуждении.

Звукопоглощающая панель, над которой необходимо поставить задачу анализа свободных колебаний, была описана выше и представляет собой конструкцию, состоящую из двух рядов полых трубчатых ячеек, выполненных из композиционного материала и заключенных в оболочку. Эта конструкция в процессе эксплуатации подвержена воздействию гармонических нагрузок как со стороны звуковой волны, так и со стороны конструктивных элементов, с которыми звукопоглощающие конструкции соединены.

Рис. 3. Двухслойная звукопоглощающая панель

На рисунке 3 представлена двухслойная звукопоглощающая панель, стрелками показано направление воздействия звуковой волны, шумов.

Диапазон частот, в котором исследуем данную конструкцию, – слышимый человеком диапазон частот: от 20 до 20000 Гц. В качестве гармонической нагрузки P на внутреннюю поверхность звукопоглощающей панели S используется гармоническая нагрузка, спектральные составляющие которой равномерно распределены в исследуемом диапазоне, то есть «белый шум», равный 133 дБ, это соответствует 100 Па.

Математическая постановка

Все виды динамического анализа основываются на следующем общем уравнении движения в конечно-элементной форме [3]:

[M]{u ’} + [C]{u’} + [K]{u} = {F(t)} ,                             (1)

где [M] - матрица масс; [C] - матрица сопротивлений; [K] - матрица жесткостей; {u”} - вектор узловых ускорений; {и’} - вектор узловых скоростей; {и} - вектор узловых перемещений; {F} -вектор нагрузок; (t) - время.

С помощью этого уравнения определяются значения неизвестных {и} , которые в любой момент удовлетворяют условиям равновесия системы при наличии сил инерции и рассеяния энергии.

Анализ свободных колебаний – это решение задачи о свободных (невынужденных), затухающих или незатухающих, колебаниях дискретной системы, которая описывается следующим уравнением движения:

[M]{u ’ ’} + [C]^u} + [K]^u} = 0.(2)

Этому уравнению придается форма, соответствующая задаче о собственных значениях. В случае затухающих колебаний уравнение имеет вид:

([K] + i to[C] - ^[M]){u} = 0.(3)

Для случая незатухающих колебаний (наиболее типичного для анализа свободных колебаний) пренебрегают слагаемым [C]^u’} , и уравнение приводится к виду:

([K] - a2 [M]){u}= 0,(4)

где ш² (квадрат собственной частоты) - собственное значение; {u} (собственные формы, не являющиеся функциями времени) – собственные формы колебаний. Формула (4.3) – так называемая обобщенная проблема на собственные значения.

Таким образом, собственные колебания конструкций определяются не только соответствующими частотами, но и формами собственных колебаний или модами, которые характеризуют относительные нормированные амплитуды перемещений точек тела. Как частоты, так и формы колебаний не зависят от способа возбуждения и амплитуд возбуждающих колебаний, а определятся жесткостными и массовыми характеристиками тела и способом его закрепления.

Анализ гармонического воздействия используется для определения параметров установившегося движения линейной системы при синусоидальном силовом возбуждении.

Разрешающее уравнение для этого вида анализа представляет собой специальный случай общего уравнения движения, в котором вынуждающая сила {F(t)} является синусоидальной функцией времени с известной амплитудой F_o и частотой ш (и фазовым углом ф):

{F(t)} = {F_o (cos( m t + ф ) + i sin( ^ t + ф ))}.                         (5)

Подставив формулу (5) в (1), получим:

[M]{u”} + [C]{u’} + [K]{u} ={F o (cos( ^ t + ф ) + i sin( ^ t + ф ))} .              (6)

Моделирование конструкции и численная реализация

Для решения задачи отклика данной сложной ортотропной конструкции на гармоническое воздействие в работе [4] рассмотрены три модели звукопоглощающей конструкции: тонкостенная однородная оболочечная конструкция с эффективными упругими характеристиками, пространственная неоднородная ячеистая конструкция с эффективными характеристиками несущих слоев, пространственная неоднородная ячеистая конструкция с перфорацией несущих слоев. Для проведения численного эксперимента использовался пакет инженерного анализа ANSYS 8.0. Во всех трех моделях материал конструкции задается как изотропный, с эффективными свойствами стеклотекстолита ВПС-33 по основе ткани ввиду сложности введения в модель реальной структуры материала панели. Для моделирования динамического отклика сложной ортотропной звукопоглощающей конструкции на гармоническое воздействие принято решение использовать пространственную неоднородную ячеистую модель звукопоглощающей конструкции с эффективными характеристиками несущих слоев, не учитывающую ортотропию материала конструкции и учитывающую перфорацию поверхностей через осредненные эффективные свойства материала, заданные по слоям, используя метод конечных элементов, который реализован в пакете инженерного анализа ANSYS .

Результаты

С помощью пакета инженерного анализа ANSYS 8.0 получены значения собственных частот панели и собственные формы колебаний при действии гармонической нагрузки - «белого шума». На рисунке 4 построена зависимость максимальных перемещений точек конструкции от собственной частоты. Использовалась пространственная неоднородная ячеистая модель звукопоглощающей конструкции с эффективными характеристиками стеклопластика несущих слоев, не учитывающая ортотропию материала конструкции и учитывающая перфорацию поверхностей через осредненные эффективные свойства материала, заданные по слоям. В таблице 1 приведены эффективные свойства звукопоглощающей панели.

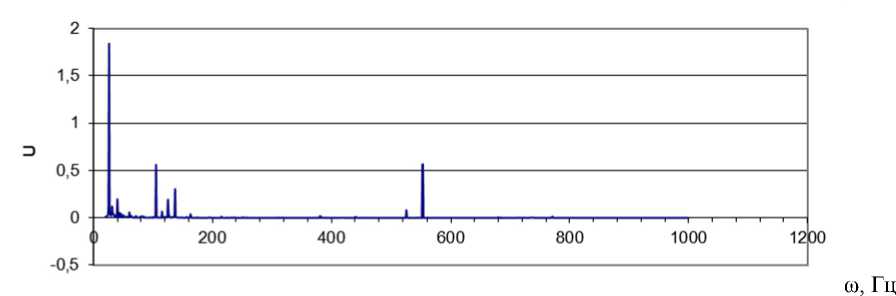
Рис. 4. Спектр вынужденных колебаний перфорированной панели из стеклопластика

Таблица 1

Эффективные счвойства звукопоглащающей панели

Слои	Модуль упругости при растяжении по основе Е , ГПа	Коэффициент Пуассона	Плотность, кг/м3	Процент перфорации, %
Наружный	24,6	0,16	1850	-
Срединный	18,6	0,11	1650	6,3
Внутренний	16,6	0,1	1450	5

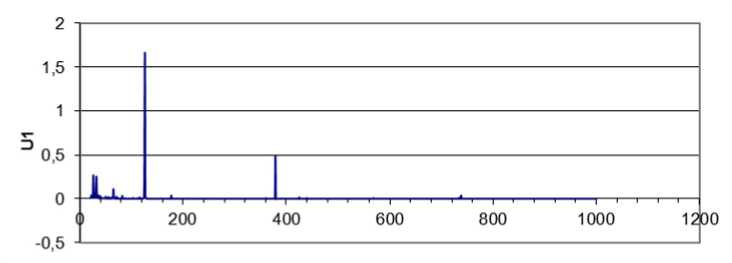
ω1, Гц

Рис. 5. Спектр вынужденных колебаний не перфорированной панели из стеклопластика

Также получены значения собственных частот и собственные формы колебаний панели, не имеющей отверстий перфорации при действии гармонической нагрузки – «белого шума». В таблице 2 приведены эффективные свойства стеклопластика данной панели. На рисунке 5 построена зависимость максимальных перемещений точек конструкции от собственной частоты. При этом использовалась все та же модель панели.

Таблица 2

Слои	Модуль упругости при растяжении по основе Е , ГПа	Коэффициент Пуассона	Плотность, кг/м3	Процент перфорации, %
Наружный	24,6	0,16	1850	-
Срединный	24,6	0,16	1850	-
Внутренний	24,6	0,16	1850	-

Для сравнения влияния материала звукопоглощающей панели на значения собственных частот и собственные формы колебаний панели исследована перфорированная панель, выполненная из углепластика. В таблице 3 приведены эффективные свойства данной панели. На рисунке 6 построена зависимость максимальных перемещений точек конструкции из углепластика от собственной частоты. При этом использовалась все та же модель панели.

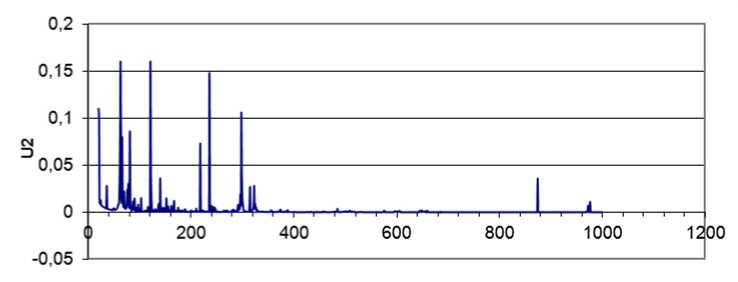
ω2, Гц

Рис. 6. Спектр вынужденных колебаний перфорированной панели из углепластика

Таблица 3

Слои	Модуль упругости при растяжении по основе Е , ГПа	Коэффициент Пуассона	Плотность, кг/м3	Процент перфорации, %
Наружный	125	0.31	1540	-
Срединный	94,5	0.25	1370	6,3
Внутренний	84,4	0.2	1207	5

Заключение

Таким образом, исследовано влияние перфорации и материала конструкции на собственные вынужденные частоты и формы колебаний.

Как видно из рисунков 4, 5, 6, перфорация и материал влияют на вынужденные частоты и формы колебаний конструкции. Наиболее значимые вынужденные частоты для перфорированной панели из стеклопластика – 26, 105 и 553 Гц; для не перфорированной панели из стеклопластика – 32, 126, 379 и 738 Гц; для перфорированной панели из углепластика – 63, 121 и 236 Гц.

При перфорировании конструкции спектр собственных частот конструкции сужается, но величина колебаний возрастает. При использовании материалов с более высокими жесткостными характеристиками спектр собственных частот конструкции расширяется, но величина колебаний уменьшается

По результатам проведенных численных исследований построена методика оценки эффективности оценки звукопоглощения конструкции на основе данных о спектре вынужденных колебаний.

Пользуясь определением децибела, можно записать уровень интенсивности звука в виде:

измеренная интенсивность

Уровень интенсивности = 10 lg                             (дБ).              (7)

эталонная интенсивность

Если измеряем звуковое давление, то формула (7.1) примет вид:

измеренное давление

Уровень звука = 20 lg                        (дБ),                               (8)

эталонное давление где эталонное давление – звуковое давление самого слабого из слышимых звуков. Оно составляет 0,00002 Н/м2.

Используя формулу (8) и приняв, что отношение измеренного и эталонного давления есть отношение измеренного и эталонного виброперемещения, получим формулу (9)

Уровень звука = 20 lg измеренное виброперемещение (дБ),                   (9)

эталонное виброперемещение где эталонное есть минимальное виброперемещение поверхности панели во всем исследуемом диапазоне частот (4х10-7 мм). Измеренное виброперемещение возьмем из результатов моделирования (рис. 4, 5, 6).

По формуле (9) нетрудно вычислить уровень звукового давления панели под воздействием гармонической нагрузки. Уровень звукового давления перфорированной и не перфорированной панели под воздействием гармонической нагрузки для значимых частот представлен в таблице 4.

Таблица 4

Тип конструкции	Частота, Гц	Величина вибро-перемещений, мм	Примерный уровень звукового давления, дБ
Перфорированная панель из стеклопластика	26	1,84	133
	105	0,56	122,9
	533	0,56	122,9
Не перфорированная панель из стеклопластика	32	0,256	116,1
	126	1,666	132,4
	379	0,496	121
	738	0,0738	105
Перфорированная панель из углепластика	63	0,159	111
	121	0,16	112
	236	0,148	111

Таким образом, методика расчета динамического поведения сложных конструкций и построения модели при помощи пакета ANSYS является достаточно простой и эффективной, что позволяет решать прикладные задачи, в частности оценка эффективности шумопоглощения звукопоглощающих конструкции при помощи компьютерного моделирования динамического поведения конструкции методом конечных элементов, а также нахождения резонансных частот конструкции. Данная методика в отличие от натурных испытаний не требует больших финансовых вложений.

Применение данной методики на стадии проектирования конструкции значительно упростит выбор оптимального процента перфорации, геометрических размеров и материала конструкции.