Коммутация спектральных делителей квадратичного пучка

Введение и основные понятия

Пучком степени k е N называется функция

L(^) = AI + А( k-1) An-1 +... + AA1 + A комплексного переменного А. Объектом наших исследований будут квадратичные пучки к = 2 с матричными эрмитовыми коэффициентами. Там, где это удобно, мы будем рассматривать коэффициенты пучка как матрицы операторов, самосопряженных относительно скалярного произведения (•, •) пространства Сn. Общая теория таких функций изложена в [1, 2] (здесь рассмотрены пучки с произвольными самосопряженными коэффициентами в гильбертовом пространстве). Известно, например, теорема 11.2 в [1], что каждый квадратичный пучок L(А) = А + AA1 + A0 может быть представлен в виде произведения L(А) = (AI — A)(AI — X). Каждый из множителей в этом разложении называется спектральным делителем пучка L. Построение спектрального делителя AI — X по заданному спектральному делителю AI — A было изучено в работе [3] в случае, когда все собственные значения матрицы A простые и различные, и работе [4] – для произвольной матрицы A . Эта задача относится к классу так называемых обратных задач, которые активно

Математика исследуются в наши дни. Обзор различных типов обратных задач для матричных пучков содержится в работе [5]. Там же и в [6, 7] можно найти приложения этих задач к различным проблемам механики. Нами рассмотрена задача описания всех спектральных делителей XI - X, коммутирующих с заданным XI - A. Получены необходимые и достаточные условия на матрицу A, при выполнении которых эта задача имеет решение и описана структура множества решений X . Рассмотрение задачи с заданным левым спектральным делителем нисколько не ограничивает общности, так как задача с известным правым спектральным делителем легко сводится к задаче с известным левым спектральным делителем. Действительно, предположим, что задан делитель XI - X и нужно определить множитель XI - A, для которого коэффициенты пучка L(X) = (XI - A)(XI - X) являются эрмитовыми матрицами. Из равенства (XI - A)(XI - X) = (XI - X*)(XI - A*) для всех Xe R следует, что по заданному левому делителю X* требуется найти правый делитель A *. После этого матрица A будет решением нашей задачи.

Основные результаты

В работе было показано, как по заданной матрице A определить все матрицы X , для которых пучок L(X) = (XI- A)(XI -X) имеет эрмитовы коэффициенты. В частности, было доказано, что в случае, когда ст(A)п ст(A*) является пустым множеством, задача имеет единственное решение X = A *, а в остальных случаях решений бесконечно много. Здесь будет выделен класс решений X , коммутирующих с заданной матрицей A . В соответствии с теоремой 5 работы [4] спектральные делители XI - A и XI - X связаны равенством X = A * + W0, где W0 является эрмитовой матрицей специального вида. Тогда условия

A + X = A * + X * , AX = X * A * , AX = XA (1) можно переписать в эквивалентном виде

AW 0 = W₀ A * , W₀ = W ₀ * , AA * - A * A = W₀ ( A - A * )                     (2)

Теорема 1. Пусть задана произвольная матрица A . Тогда следующие условия равносильны: 1) система (2) имеет решение W ₀ ;

2) матрица A представима в виде A = tAt ¹ , где T ¹ = T * ,

^

A =

^ ^A 11

I ⁰

A 22

*

^A 22 = ^A 22

и матрица A ₁₁ удовлетворяет условиям

( ^A 11 ^{- A} 11 ) ^A 11 ( ^A 11 ^A 11 ^{- A} 11 ^A 11 ) = ( ^A 11 ^A 11 ^{- A} 11 ^A 11 ) ^A 11 ( ^A 11 ^{- A} 11 ) , ( ^A11 ^{- A} 11 )( ^A 11 ^A11 ^{- A}11^A11 ) = ( ^A 11 ^A11 ^{- A}11^A11 )( ^A 11 ^{- A}11 ) .

При выполнении условий матрица W 0 имеет вид

W 0

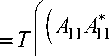
- 1

⁰ ( T - 1

— д д Ид -д I

^A 11 ^A 11 )( ^A 11 ^A 11 )

где W ₂₂ - любое решение уравнения A₂₂W₂₂ = W ₂₂ A ₂₂

Доказательство. Пусть матрица W0 является решением системы (2). Рассмотрим некоторый ортонормированный базис £ = {£1,£0} пространства Cn, где f1 является базисом подпространст ва ran (A * - A), а £0 является базисом подпространства ker (A * - A). Пусть T - матрица перехо да от базиса £ к стандартному базису пространства. Тогда T-1 = T*. Обозначим A = T-1 AT, W0 = T-1W0T . В силу условия T-1 = T* равенства (2) равносильны аналогичным равенствам для матриц Л и Wo. Представим матрицу A в виде

A=

( A

v A 21

A 12

A ₂₂

.

В силу выбора базиса £ выполнены равенства A ₂₁ = A 12 , A ₂₂ = A 2 ₂.

Так как W _o ( A

*

и матрица A ₁*₁ - A₁₁ невырождена, то мат-

рица W ₀ имеет блочно-диагональную форму:

W o =

.

W 22

Теперь система (2) для матриц A и W ₀ принимает вид

' A ll

A 12

r W ll

0

1

r W ll 11

0

1

A11

A

1

*

v A 2

A 22 A

V 0

W 22

J

V 0

W 22

A

V A 1*2

A 22 A

J

^11 = W ll , W 22

= W 22

r A 11

12

' All

A 12 ^

A 11

A 12 '

r

A 11

А A 12

r W ll ( A - A * )

0 1

I

V A 12

A 22 A

v A 2

A 22 A

v A 12

A 22 A

v

A 12

A 22 A

v       0

0 A

.

;

Приравнивая правые верхние элементы в последнем равенстве системы (5), получаем ( A₁₁ - A ₁*₁ ) A ₁₂ = 0. Это означает, что A ₁₂ = 0 и мы можем записать систему, равносильную системе (5):

A 12 = 0, A 22 W 22 = W 22 A 22 , A 11 W 11 = W ll All ,

W 11 = W l , A ll Ail — Ail A ll

Заметим, что уравнение A₂₂W₂₂ = W ₂₂ A ₂₂ имеет решение W ₂₂ для любой матрицы A ₂₂. Следовательно, система (6) имеет решение тогда и только тогда, когда A ₁₁ удовлетворяет условиям

A ll ( A ll A ll

1 ^- A ll )   = ( A ll A ll

1 ^- A ll ) A ll ,

_ ( A ll 41

11 ^- A ll )  ( A ll A ll ^- A ll A ll ) .

Очевидно, что эти условия равносильны условиям (4) и г

[                        1

11    A ll ) .

Пусть теперь выполнено условие 2. Непосредственно проверяется, что A и W0 удовлетво- ряют системе (2). Тогда A = TAT

¹ и W _o = ПГ 0 T

¹ c T

1     'Т7*

= T также удовлетворяют этой системе

• (2)    и X = A * + W ₀ является решением системы (1).

Следствие 2. Пусть задана матрица A . Система (1) имеет единственное решение X = A * тогда и только тогда, когда ker ( A * - A ) = { 0 } и матрица A удовлетворяет условию (4) теоремы 1.

Замечание 3. Из доказательства теоремы 1 следует, что в качестве T можно брать матрицу перехода от любого ортонормированного базиса, построенного по разложению С n = ran ( A * - A ) © ker ( A * - A ) , к стандартному базису пространства С n .

Теорема 4. Пусть дана произвольная матрица A . Тогда следующие условия равносильны:

• 1)    система (1) имеет решение;

• 2)    матрица A представима в виде A = TAT ¹, где T

  
  

  ¹ = T * , B A = diag { A_bA ₂ } и

  
  

2а) A ₁ – произвольная диагональная матрица;

2b) матрица A ₂ представима в блочном виде, где все вне диагональные блоки нулевые, а каждый диагональный блок имеет вид

Математика

A l =

' 0,5 ад + A/         Di v D      -0,5iAlIl + D AiDi-

,

где D i - произвольная невырожденная матрица, A ’ = A ’ , X i e c r( A ) , X i Ф 0.

Доказательство. Пусть система (1) имеет некоторое решение X = A + W₀, где A и W ₀ связаны равенствами (2). Перейдем от матриц A и A * к матрицам A и A * в некотором ортонорми-рованном базисе £ , построенном по разложению С n = ker ( A * - A ) © ran ( A * - A ) . Пусть T -

матрица перехода от базиса £ к стандартному базису пространства С ⁿ . Тогда A = TAT 1 , W ₀ = TW₀ T ^{- 1} и T ^{- 1} = T * . Из (2) и равенства T ^{- 1} = T * вытекает включение

A - A ) c ker ( AA - A A ) . Поэтому

A * - A = diag { 0 ■ 1 0 , A } ,                                     (7)

AA * - A * A = diag { 0 ■ 1 0 ,D } .                                  (8)

Согласно теореме 1

DA= -AD, где матрицы A, D имеют размер, равный размерности пространства ran (AA* - AA). Отсюда следует, что каждый собственный вектор матрицы А, отвечающий собственному значению Л Ф 6, переводится матрицей D в нулевой вектор или в собственный вектор Df матрицы A , отвечающий собственному значению -Я. При этом если Df Ф 6, то он переводится матрицей D в собственный вектор D2 f матрицы А, отвечающий собственному значению X. Чтобы это доказать, нужно исключить равенство D2 f = 6. Предположив противное, получим, что Df Ф 6 и D2 f = 6. Но это невозможно, так как матрица D кососимметрическая. Обозначим

£ 1 ( i ^ .) = { f e С ⁿ : А f = i j , Df = 6 } , j = 1,..., k ;                     (9)

£ 2 ( ± i 2 j ) = { f e С ⁿ : А f = ± i X . f , Df Ф 6 } , j = k + 1,..., 5 ;                (10)

£ 0 = ker ( A - A * ) .

Заметим, что некоторые собственные значения из (9) могут совпадать с собственными значениями из (10). Из приведенных выше рассуждений следует, что dim £ 2 ( i X . ) = dim £ 2 ( - г' Я . -) и

D£ 2 ( ± i ^ j ) = £ 2 ( + i j .

Представим пространство С ⁿ в виде ортогональной суммы С n = £ 0 © £ 1 © £ 2 ,

где

£ 1 = £ 1 ( Ц ) ©...© £ 1 ( i X k ) , £ 2 = £ 2 ( i A _k + 1 ) © £ 2 ( - i A k + 1 ) © ^ © £ 2 ( i A _s ) © £ 2 ( - i A _s ) .    (12)

Теперь будем считать, что ортонормированный базис £ состоит из объединения ортонорми-рованных базисов, выбранных в каждом из слагаемых в разложении (11), (12) пространства С n .

Тогда матрицы A - A и AA

- A A b построенном базисе £ имеют вид

A * - A = diag { 0 ■ 1 0 , i ^ I 1 ,^, i A k l k , А k + 1 ,^, А 5 } =

= i ■ diag < 0 ■ I о , Л 1 1 1

, ^ , A k I k , A k + 1

k + 1

0 )

^- I k + 1 )

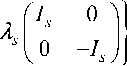
AA - A * A = diag { 0 ■ 1 0 ,0 ■ 1 1 ,^,0 ■ I k , D k + 1 ,_D 5 } =

= diag <  0 • 1 0 ,0 • 1 1

,•,0 • Ik,

Г 0

I D +

D k + 1

Г 0

, • • •,

D * 0

.

Возможно, что ker ( A * - A ) = { ^ } . В этом случае матрица 1 ₀ будет отсутствовать в наших представлениях. При определении матриц D _l было показано, что они являются обратимыми для всех l = k ,..., s .

^

^

Запишем матрицу A в блочном виде A = ( A m )

m , l = s ,                 /^x

1 m l = 0 в базисе £ . Из (7) следует, что

A m , _l = A * , m для всех l * m , A l * - A ll = iAiIi для всех l = 0, •, k ,

A ll    A ll = i Al

I_l 0

0 ]

I для всех l = k + 1, •, s .

Равенства (16) означают, что матрицы A_ll можно представить в виде

A_ll = - 0,5 i A _lI_l + A_l для всех l = 0, •, k .

Следовательно, существует ортогональная матрица T_l , для которой

A ll = T l ( - 0,5 i A l I l + E l ) Tf¹, E l — вещественная диагональная матрица, l = 0, •, k .

Таким образом, с учетом теоремы 1 доказано представление матрицы A ₁ .

Равенство (8) с учетом (7) принимает вид

A • diag { 0 • 1 0 ,A } - diag { 0 • 1 0 ,A } - A = diag { 0 • 1 0 ,D } .

Из последнего равенства получаем, что для каждого l = 1,2,…, k

( Au • a iA kl • i ^ l i l A k + 1, l • i ^ l i l • A sl • i ^ l i l A s + 1, l • i ^ l i l ) T =

= ⁽ i A 1 1 1 • A 1 1 i A k I k • A kl A k + 1 • A k + 1, l A s • A s , i Следовательно, A ml = 0 для всех m = 1,^, k и m Ф l .

Далее из (20) для каждого l = k + 1, k + 2, •, s :

A k + 1, l "  A l    A l , l "  A l    A sl "  A l    A s + 1, l •

^l • a I • A kl   A k + 1 • A k + 1, l • A l • A ll + D l • A S • A sl

Отсюда

A_ll • A _l = A _l • A_ll + D_l , l = k + 1,-, s .

Непосредственной проверкой из последнего равенства получаем, что матрица A ll имеет вид

A ll =

*

Запишем матрицы A , A -

A l l

D

2 Z ^l

для всех l = k +1,..., s .

- ^ D * ( 2 ^ l ^l

.A , .A * . A - .A .A *

A ll

в блочном виде относительно разложения

C n = £ 01 © £ 2 , где

в виде

A =

' A 11 . An

A ₁₂

A 22 J

, A * - A =

, A = A 22 J

' 0

. 0

.

Из первого равенства системы (4) вытекает равенство

0  An • ,A12 • d22 л

0 A 22 • A 22 • D 22 J

D22 • kA*2 • A

*

D 22 A 12

.

Математика

Так как в построении ненулевых элементов матрицы A 11 • Л ₁₂ • D 22 участвуют обратимые блоки из A₁₁ и D₂₂, то A ₁₂ = 0 .

Так как все матрицы в равенстве A22 • Л22 • D22 = -D22 • 1A22 • A22 имеют блочно-диагональный вид, определяемый равенствами (14), (17) и (23), то мы получаем равенства f i^iIi . 0

- i λ _lI_l

A l ^′ l

D

2 λ _l ^l

_- i _D ∗ 2 λ _l ^l

A l ^′ l ^′

f 0 D l

D l 0

f 0

. D l

l

A_l ′ _l

D

2 λ _l ^l

_- i _D ∗ 2 λ _l ^l

A l ^′′ l

f i ^ i I i . 0

- i λ _lI_l

для всех l = k +1,..., s .

Отсюда и из (17) следуют равенства

A ’ - A l = i ^ l I l , A l l' — A u = — i ^ l I l , A l D l = D l AF Д ^ля всех l = k + 1,^, s , A l ’ = D;A ’* D^^x = - 0, 5i A _lI_l + D ^ A ’ D^^x для всех l = k + 1, ^, s .

w

w

w

С учетом равенства A ₁₂ = 0 это завершает описание матрицы A ₂ и всей матрицы A .

Пусть теперь выполнено условие 2. Тогда выполняются условия (4) теоремы 1. Значит, система (1) имеет решение.

Пример 5. Используя теорему 4, опишем множество матриц A второго порядка, для которых существуют коммутирующие делители X . В этом случае возможны два варианта:

A = TAT ^{- 1} , A

A = T

μ + i λ ν

– диагональная матрица или v V ,

T 1 , ц , A , v e R, v * 0 . μ- i λ