Коммутант оператора Поммье в пространстве целых функций экспоненциального типа и полиномиального роста на вещественной прямой

В настоящей работе изучаются свойства коммутанта оператора Поммье Do в пространстве Hq целых функций экспоненциального типа, изоморфного сильному сопряженному к пространству Фреше E (Q) функций, бесконечно дифференцируемых на интервале Q С R. Ранее оператор Do и его одномерное возмущение Do,g₀ изучались в [1-4] в счетном индуктивном пределе E весовых пространств Фреше целых функций (если go = 1, то Do = Do,_g0Y В. А. Ткаченко [5, 6] использовал оператор Do,_g0 в случае go = e^P,

где P — некоторый многочлен (см. [1]). В [5, 6] он действует в (БВ)-пространстве целых функций, рост которых определяется р-тригонометрически выпуклой (р > 0) функцией со значениями в (-то, +то]. Сопряженный к нему назван в [5] оператором обобщенного интегрирования. Конструкции подобного рода в (БВ)-пространстве целых функций экспоненциального типа использовались И. Ф. Красичковым-Терновским [7]. В [1] был исследован коммутант Do,g₀ в кольце всех линейных непрерывных операторов в Е. Свойства алгебры, образованной сопряженным Е‘ к Ес умножением, определяемым оператором сдвига для Do,g0, изучены в [2], циклические векторы и собственные замкнутые инвариантные подпространства Do,g₀ в Е описаны в [3, 4]. Существенным отличием рассматриваемой здесь ситуации от изученных ранее конкретных случаев является неквази-аналитичность пространства E (П), изоморфного сопряженному к Hq (в [3, 4] сопряженное к Е реализуется как некоторое пространство аналитических функций). Следствием этого является отсутствие циклических векторов у оператора Поммье в Hq. В ситуациях, исследованных в [3, 4], циклическими векторами Do являются все функции из Е, отличные от многочлена (т. е. их «больше», чем функций, не являющихся циклическими).

Основной целью данной работы является описание линейных непрерывных в Hq операторов, перестановочных в Hq с Do и являющихся изоморфизмом Hq или близких к нему. Всякий оператор B из ком мутанта K (Do) оператора Do задается некоторым линейным непрерывным функционалом у на Hq. С учетом рефлексивности E (П) и теоремы Пэли — Винера — Шварца сопряженное к Hq можно отождествить с E (П), и тогда элементы K (Do) определяются (однозначно) функциями из E (П). Показано, что изоморфизм задается той и только той функцией, которая не равна 0 в начале координат. При этом существенную роль играет метод, использующий теорию компактных операторов в банаховых пространствах. Ранее в аналогичных вопросах он применялся В. А. Ткаченко [6]. В другом крайнем случае, когда бесконечно дифференцируемая в П функция обращается тождественно в 0 в некоторой односторонней окрестности начала координат (и интервал П с соответствующей стороны ограничен), она задает несюръективный оператор. Как показано в [1], с помощью оператора сдвига для оператора Поммье в сопряженном HQ к пространству Hq можно ввести ассоциативное и коммутативное умножение. Его естественной реализацией в E (П) является произведение Дюамеля, играющее важную роль в различных вопросах анализа (см., например, работы М. Т. Караева [8, 9]). Это произведение тоже существенно используется в доказательствах.

• 1.    Вспомогательные сведения

Пусть П — пите'рвал в R. содер»капни! 0: (Kn)neN — исчерпывающая П последовательность отрезков: Kn С intKn+i, n Е N; П = U_neN Kn. При этом для множества M С R ашвол int M обозначает внутренность M в R. Будем счсстать, что 0 Е Ki- Пусть H m (x) := supyeM(xy) - x Е R. — опорная фуикипя множества M С R: A(C) — пространство целых в C функций.

Далее для n Е N

HQ,n ^:= ^ff ^{Е A(C) :} Ilflln ^:= sup            ^lf (z^— ----- < +ro| ;

zee ^{(1 + |z|)n} exp⁽HKn⁽Im ^z))

HQ,n является банаховым пространством с нормой || • ||_n. При этом HQ,_n С HQ,n+i, n Е N, и эти вложения непрерывны. Положим Hq := UneN HQ,n ^{и сна}бдим Hq топологией индуктивного предела пространств HQ,n, n Е N, относительно их вложений в Hq.

Положим ед(х) := e^-iAx. x,A G C. Для локально вытчалого пространства X символ X‘ обозначает топологическое сопряженное к X. Пусть E (П) — пространство Фреше всех бесконечно дифференцируемых в П функций. По теореме Пэли — Винера — Шварца [10, теорема 7.3.1] преобразование Фурье — Лапласа F(у)(А) := у(ед), A G C, у G E (П)’, устанавливает топологический изоморфизм сильного сопряженного к E (П) нa Hq. Отметим, что E (П) рефлексивно.

Пусть L(Hq) — пространство всех липейиьix непрерывных операторов в Hq. Оператор Поммье Dz, z G C, определяется равенством f (t)-f (z)

t = z, t = z,

Dzf№:= (f - '

f G Hq. По [1] Dz G L (Hq) для л тобого z G C.

Следуя [11, 12], введем сдвиги Tz, z G C, для Dq, линейно и непрерывно действующие В Hq: ДТЯ f G Hq tf(t)-zf(z)

t = z, t = z.

Tz(f)(t) :=       t-z   ’ .

f (z) + zf (z),

Пусть K (Dq) — множество всех линейных непрерывных операторов в Hq. перестановочных с Dq в Hq, т. е. коммутант Dq в ко льце L (Hq).

Теорема 1. Следующие утверждения равносильны:

• (1)    B G K (Dq).

• (ii)    Существует функционал у G HQ тако й, что B(f)(z) = y(T_z (f)), z G C, f G Hq.

• <1 Из [1. теорема. 15] следует справедливость теоремы. ▻

• 2.    Основной результат

Для у G HQ ножжим B^(f)(z) = у^(f)). z G C f G Hq.

Определим бинарную операцию 0 в Hq : (у 0 ^)(f) := у_z(^(Tz(f)), у, ф G HQ, f G Hq. По [1, §3] произведение у 0 ф корректно определено; оно ассоциативно и коммутативно. Кроме того [1, следствие 18], отображение к(у) := В^ является изоморфизмом алгебр (HQ, 0) и K (Dq) (в последней вводится обычное операторное умножение).

Как обычно. D(R) — пространство всех беекозтечпо дифференцируемых в R функций с компактным носителем. Для обобщенной функции u G D‘(R) символ supp(u) обозначает носитель u. Отметим свойство равномерной ограниченности носителей обобщенных функции F^-1(T_z(f)). z G C. для фиксиров<ишой функции f G Hq.

Лемма 1. Для любых m G N f G HQ,_m, z G C, носи тели F ^-1(Do(f)) и F ^-1(T_z (f)) содержатся в Km.

< Применяя принцип максим ума модуля, получаем, что ||DQ(f)|_m< +ж ii

T (f )(t)l

sup (1 + |t|)m+1 exp(HKm (Im t))

< +то.

По теореме Пэли — Винера — Шварца supp(F 1(Do(f))) С Km и supp(F ¹ (Tz(f))) C Km- ▻

Для локально выпуклого пространства X, линейного непрерывного оператора A : X ^ X элемент x G X называется идк.ожтки.м вектором A в X. если система, {An(x) : n ^ 0} ползia в X. т. е. ее линейная оболочка плотна в X.

Следствие 1. Оператор Do не имеет в H q ни одного циклического вектора.

<1 Зафиксируем f G HQ,m. По лемме 1 носитель каждой обобщенной функции F^-1(Dn(f)). n ^ 0. содерлентся в Km. Возьмем ненулевуто функцию h G D(R) такую, что (supp(h)) П Km = 0iI supp(h) С П. Тогда F -1(Dn(f ))(h) = 0 для лтобого n ^ 0. Значит, множество {F -1(Dn(f )) : n ^ 0} не является полным в сильном сопряженном к E (П). следователь!ю. множество {D0(f ) : n ^ 0} не являете!i полным в Hq. >

Этот факт принципиально отличает рассматриваемую здесь ситуацию от изученных ранее. Он влечет также, что семейство собственных замкнутых Do-инвариантных подпространств Hq очень широкое.

Пусть S(R) — пространство Шварца всех бесконечно дифференцируемых функций h : R ^ C таких. что limt^^(|t|^k|f^(k)(t)|) = 0 для любого k G N. Сняво.лом F s обозначим преобразование Фурье, действующее в пространстве S‘(R) обобщенных функций медленного роста на R.

Для h G S (R) введем <функцию k(h)(z) := f+^ h-) dt- z G C\R.

Лемма 2. Пусть h G S(R) и A := f+2 h(t) dt. Toгда lim z^c», (zk(K)(z)) = —A.

Это утверждение содержится в [13, гл. 4, § 71]. Поскольку функции h и hi(t) := th(t) принадлежат S(R), то найдется C >  0 такое, что для любых ti,t2 G R, для которых |ti|, |t2| ^ 1- выполнятотюI неравенства |h(ti) — h(t₂)| С C | "у — -2 | ii |hi(ti) — h1(t₂)| С C I"1 — "2I *^{т е}" ^{в те}Р^^пшолопш [13] h ii hi удовлетворитот условию H волызи то). Кроме того, существуют пределы lim z^ra, k(hi)(z) и lim z^^, k(hi )(z), равные 0. Поэтому

Im z> 0               Im z< 0

lim z^ra, (zk(h)(z)) = —A no [13. c. 260].

zGC\R

ЗАМЕЧАНИЕ 1. (i) Преобразование F : у H- (у(ед),А G П) является топологическим изоморфизмом сильного сопряженного к Hq нa E(П). При этом F — отображение, сопряженное к F : E(П)’ ^ Hq относительно дуальных пар (E(П)’, E(П)) и (Hq,HQ).

Полагаем у := F(у), у G Hq. Для любых у G Hq, n ф 0, справедливо равенство —⁽ⁿ⁾(0) = ^t(tn).

• (ii)    Операция 0 посредством F : Hq ^ E (П) иидутнтруст в E (П) произведение Дтоа-

  .---

  
  

  -----

  
  

меля. т. е. у 0 ф = у * ф. где

(g *h)(t) = ddt

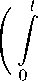
g(t — T )h(T) dr^

t

= g^(0)h(t) + j ^g(t

— t )h(T) dT,

g,h G E (П).

• (iii)    Билинейная форма (f, h) := F 1(h)(f), f G Hq, h G E (П), задает двойственность между Hq i i E (П). При этом (f, h) = F ^-1(f )(h)-

• Сопряженным к оператору B^ : Hq ^ Hq, у G Hq, относительно этой двойственности является оператор A^ : E(П) ^ E(П), A^p(h) = <-* h.

Выясним далее, при каких условиях Б_ф является изоморфизмом Hq. Вначале охарактеризуем инъективные операторы Б^.

• Лемма 3. Следующие утверждения равносильны:

• (i)    Б_ф ииъектпвеп в Hq.

• (и) ^-(0) = ⁰

• < (i)^(ii): Если —(0) = 0, то Б^(1) = 0 (стоящая в скобках функция тождественно равна 1). Поэтому оператор Б_ф не является инъективным.

(ii)^(i): Пуоть f Е Ker B^. Тогда у(Т(f)) = 0 для лтобого z Е C. Следовательно. F^—^уфТ (f )) = 0 и F^-1(T_z(f ))(?) = 0 для лтобого z Е C. По лемме 1 существует m Е N. для которого носители в<-ек обобщенных функции F^-1(Tz(f)). z Е C. содержатся в Km. Возьмем функцию х Е D(R) такук>. что х равна 1 в Km+i 11 supp(x) С П. Тогда F^-1(Tz (f)) (х'7?) = 0. z Е C. Таким образом.

Fs¹ (хУ)№ (f ) I r) = 0, z Е C.

Функция g := ^^—1(х9?) принадлежит S(R) (при этом S(R) отождествляется стандартным образом с подпространством S '(R)). Значит,

+^               +^

f t^{f (t)}g^(t)              х [ g^(t)

---------dt = zf (z)    ----- dt, z Е C\R.

J t - z             J t - z

—^               — ^

Положим	+^                 +^ a(z) := [ t f (t)g(t) dt, e(z) := [ -g^ dt, z Е C\R. t - z                   t - z ^                —^
По лемме 2	+^ lim   (ze(z)) = - [ g(t)dt = -х(0)у(0) = 0 z^^,z£C\R — ^

(функция tf (t)g(t). t Е R. прина,пежит S(R)). Поскольку limz >^, a(z) = 0. to zeC\R limz^^ f (z) = 0 ii. следователыю. f = 0. Значит. Ker Вф = {0}. >

Введем функционалы 5o,n Е Hq, n ^ 0 : 5o,n(/) := n f ⁽ⁿ⁾(0), f Е Hq. Заметим, что 6₀,n(x) = nyxn, x Е П, и к(^о,_п) = By, „ = Dn [1, лемма 7] (отображение к : Hq ^ K (Do) введено в § 1).

Лемма 4. Пусть у Е H’^ п у^^б) = 0. 0 С j С n - 1- для штсоторого n Е N. Тогда существует ^ Е Н^ таксав что у = ^0,n 0 ^- Если у?^(п)(0) = 0, то yi(0) = 0.

<1 Поле >жим ^ := ,F—1(?(n)) 11 h := у?. Тогда

h ( t ) =

1 d n! dt

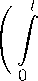
(t - т)ⁿh^nnHT ) d^

t Е П,

t. e. 5o,n * h⁽ⁿ⁾ = h- Отсюда следует равенство у = 5o,n 0 F ¹(h⁽ⁿ⁾). >

Введем дуальные преднормы в Н^- Цу^П := supf ^н_п, |y^(f)|. n ^Е N. у ^{Е Н}

Ilf In<1

Теорема 2. Следующие утверждения равносильны:

И B_v Е K(Dogo ) — II3OMOp(l)II3M Hq.

(и) ^w = 0

< (ii)^(i): Используем метод доказательства В. А. Ткаченко [6, теорема 2]. Поскольку для f Е Hu- t = z tf (t) - zf (z) = f (z) + tf (t) - f (z)

t - z                  t - z

By(f )= ?(0)f + B(f ), B(f )(z):= Уt(tDz(f )(t)), z Е C, f Е H_Q.        (1)

Покажем, что B — лииеПныП непрерывный оператор в Hq такой. что для любого n Е N сужение B на HQ,n — компактньш оператор в HQ,n. Зафиксируем n Е N. Положим Sn = {f Е HQn : ||f ||n Д 1}. Для любо!i функции f Е Sn

|t|D (f )(t)|

IMtDz(/ )(t))l a Mnw sup (1 + |iDn+1 exp(HKn+i (Im,))•

Зафиксируем e >  0. Ес -ли z Е C. |t — z| Д |. то для лтобо!! функции f Е Sn

№ (f )(t)|          =             |t||f (t) — f (z)|

(1 + |t|)n+1 exp(HKn+i(Imt))    |t — z|(1 + |t|)n+1 exp(HKn+i(Imt))

a e (т^Щ + (1 + |z|)n eXP(HKn (Im z))) a 2e(1 + |z|)n eXP(HKn (Im z))-

Если же |t — z| Д 1 для z Е C, то для лтобой функции f Е Sn по принципу максимума модуля найдется w Е C такое, что |w — z| = 1 и выполняются следующие неравенства:

№(f)(t)|        _{a e}___________1___________

(1 + |t|)n+1 exp(HK„+i(Imt))     (1 + |t|)n exp(HK„+i(Imt))

x((1 + |w|)n exp(HKn(Im w)) + (1 + |z|)n exp(HKn(Imz)))

^{a e} ( 1 ^{1 +} ^l^ ^|t| ) exP (^) ^{+ (1 +} ИГ exp⁽HKn^(Imz)))

a e( (! + |) 'e^)

+ (1 + |z|)n exp(HKn(Imz))) ,

где Cn := max|^|=1 HKn(Imф) < +w. IE: (2)—(4) следует, что lim sup z→∞ f∈Sn

|B (f )(z)|

= 0.

(1 + |z|)n exp(HKn (Im z))

Последнее влечет относительную компактность B (Sn) в Hu,n. По лемме 3 оператор B^ инъективен. Поскольку <д(0) = 0, то вследствие (1) он является изоморфизмом каждого пространства Hun, n Е N. Отсюда следует, что B^ — изоморфизм Hq.

(i)^(ii): Если <д(0) = 0. то по .темпе 3 В^ не является iшъектпвиым. >

Следствие 2. Пусть ^ Е HQ ii 9?^(j)(0) = 0. 0 Д j a n — 1- ty⁽ⁿ^ (0) = 0 для некоторого n Е N. Тогда слтцествует Д Е HQ. для ювторого B_v = D0By 11 By — топологический изоморфизм Ha.. Кроме того, B^ : Hq ^ Hq имеет линейный непрерывный правый обратный.

<1 По лемме 4 существует Д Е HQ такое, что р = ^0,n 0 Ди y;⁽ⁿ⁾(0) = 0. Тогда B_v = B^_{0 n} By = D0By = ByDy. По теореме 2 By — изоморфизм Hq. Поскольку оператор Dn : Hq ^ Hq сюръективен, ядро Ker B_v = Ker Dn n-мерно (а значит, топологически дополнимо в Hq), то B^ : Hq ^ Hq имеет линейный непрерывный правый обратный. >

Обратимся теперь к другой крайней ситуации, когда функция <д является «очень» плоской в начале координат, т. е. она равна 0 в некоторой односторонней окрестности начала координат.

ЗАМЕЧАНИЕ 2. Рассмотрим случай, когда интервал П отличен от прямой R. Тогда Q = (w^-,w⁺). где хотя б^ы одно из ш-. ш⁺ конечно. Пусть. например. ш⁺ Е (0, +то).

Предположим, что д = 0 в некоторой правосторонней окрестности начала координат. Тогда найдется ненулевая функция h € E (П) такая, что h = 0 в (w+,wo] для некоторого wo € (0,w+) 11 Jot

— т )h(T ) dT = 0 для лтобого t € П. Зиа лит. А^(К) = д * h = 0. Оператор A^ : E (П) ^ E (П) является сопряженным к B^ : Hq ^ Hq (относительно дуальной пары (Hq, E (П))). Taiс как Ap пеинъективеи. то по [14. гл. 8. § 8.G] Im B^ не является плотным в Hq и, тем более, Б^ : Hq ^ Hq несюръективен.

Аналогично, если w- конечно и = = 0 в некоторой левосторонней окрестности начала, то оператор B^ : Hq ^ Hq песюръективеи. причем его образ лаже не плотен в Hq.

Приведенные рассуждения имеют непосредственное отношение к теореме Титчмарша о свертке [15]. Ее доказательство с использованием только теории функций вещественного переменного дано в [16, гл. II], в [17] оно проведено методами функционального анализа. О делителях нуля свертки Дюамеля речь идет в монографии И. Димовского [18, §1-1].