Коммутативная алгебра скалярных кватернионов

Обычный кватернион был введен как векторное расширение над полем комплексных чисел [1, 2]. Его векторная часть представляет из себя обобщенную мнимую часть и образует трехмерное кватернион-векторное пространство. Хотя кватернионы и не входят в стандартный математический аппарат, они нашли многочисленные применения в вычислительной математике (например, обработка, изображений) и многих областях физики включая специальную теорию относительности и оптику, теории элементарных частиц и астрофизику, теорию поля и механику. Например, в физике пучков заряженных частиц кватернионы весьма, эффективны в решении проблемы транспортировки спина. [3, 4].

Нередко в аналитических исследованиях и моделях мы сталкиваемся с выражениями, содержащими как комплексные числа, так и (2 х 2)-матрицы. Матричное представление, однако, может иметь и более удобные альтернативы. Квантовая механика, к примеру, может быть элегантно сформулирована, с помощью геометрической алгебры. В некоторых других ситуациях более удобно иметь дело с преобразованиями полностью скалярных выражений, чем с традиционными кватернионами — носителями векторных свойств. В общем случае могут встречаться также и комплексные функции. Соответствующие практические случаи включают, например, анализ собственных мод некоторых граничных задач [5, 6], транспортировку пучка, заряженных частиц и его динамику в ускорителях [7] и вакуумных электронных приборах [8, 9]. Можно предположить, что пространство псевдоскалярных чисел может неявно включать и элементарные матричные преобразования через расширенные свойства, скалярных кватернионов. Это пространство суть объединение двух независимых полей обычных комплексных чисел (ассоциированных, например, с временной и пространственными координатами).

Л. Левин фактически одним из первых применил скалярные гиперкомплексные величины для анализа, электромагнитных волн распространяющихся в различных волноводных структурах [6]: с диэлектриком и намагниченным ферритом, поверхностной

анизотропией и гофрами. Он ввел феноменологически дополнительную мнимую единицу (см. (1.1)) чтобы различить комплексные числа, отвечающие за различные свойства временной переменной (и/либо продольной фазовой координаты) — с одной стороны, и пространственных (либо поперечных/угловых) переменных — с другой стороны. Соответствующие мнимые единицы образуют коммутативную группу:

г² = — 1, 7² = — 1, ij = ji т^—1 или V—1-                    (1-1)

Используя этот подход, Л. Левин получил компактное скалярное дисперсионное уравнение для нормальных мод с четырехкомпонентными комплексными числами. Дальнейшее развитие этого метода [10, 11] позволило строго охарактеризовать самосогласованную систему, в которой пучок взаимодействует с замедляющей структурой и соленоидальным полем. Было показано [10], что обычный матричный подход дает эквивалентное решение системы дисперсионных уравнений и приводит в конечном итоге к точно тем же значениям инкремента и порогового тока регенеративной поперечной неустойчивости «обрыва пучка». Однако использование скалярных кватернионов значительно упрощает выкладки и дает гораздо более прозрачное физическое решение. Например, коллективная частота z>, найденная алгебраически из единственного гиперкомплексного дисперсионного уравнения, имеет четкий смысл своих компонентов: Нег Верз — расстройка коллективной частоты по отношению к собственной частоте; Тш^Тш^г/ — угловая скорость вращения вырожденной коллективной дипольной моды; а 1тг Re^z) ± Im? Re^z> дают инкременты право- и левополяризованных коллективных мод гиромагнитной неустойчивости. Заметим, что в работе [7] отсутствие дополнительной мнимой единицы привело к некорректному смешиванию между различными степенями свободы и ошибочному результату для порогового тока неустойчивости «обрыва пучка» в присутствии поперечного движения.

Коммутативная алгебра для соответствующих гиперкомплексных чисел была введена в [10] для приложений физики пучков и ускорителей. Она была определена как замкнутое обобщение над различными i- и фполями комплексных чисел, которые образуют коммутативную алгебру 4-го ранга с делением и основными атрибутами обычных комплексных чисел. В этой статье мы приводим основные свойства и простейшее аналитическое продолжение. Мы подразумеваем эквивалентными такие термины как: «четырехкомпонентное число», «гиперкомплексное число» и «скалярный кватернион».

• 2.    Элементарные свойства коммутативной алгебры четырехкомпонентных чисел

Выпишем четырехкомпонентное комплексное число, которое выглядит здесь идентичным обычному кватерниону:

a = Q₀ + io^ + ja₂ + i-joty                            (2.1)

где компоненты «о, «1, «2, «з вещественны; г, j — независимые мнимые единицы, и ij — составная мнимая единица.

Мы рассматриваем в данной работе гиперкомплексные числа (1.1), (2.1) как обладающие коммутативностью и ассоциативностью, дистрибутивностью и замкнутостью по отношению к умножению и делению.

В частности, произведение двух простых комплексных чисел из различных i- и j- пространств образует скалярный кватернион:

(а + zb) • (с + jd^ = «о + шх + ;а₂ + ijay

(2-2)

где «о = ас, од = Ьс, 02 = ad, «3 = bd.

Можно рассматривать пространства обычных комплексных чисел как двухмерные проекции пространства гиперкомплексных чисел. Поэтому естественно переопределить операторы реальной и мнимой частей следующим образом:

Rej d = о₀ + ;а2, 1т_г а = ах + ;а₃,                      (2.3)

где индексы г и j обозначают соответствующее пространство-проекцию как область действия соответствующей операции.

Рассмотрим теперь матрицы Паули

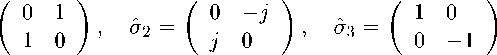
как операторы действующие, например, только в 7-пространстве. Тогда, полагая, что а Re7d \ есть матрица-столбец

_  , мы можем перейти к нашему псевдоскалярному про странству используя следующие правила подстановки:

aid -Д jd*^}', о^а ^—a, d₃d -д а*Ё                      (2-4)

• т. е. матричные операторы могут быть представлены формально как од -д j^V³, 02 ^ -1, и d₃ -^ (-)*т

Подобно алгебре спиновых матриц из (2.4) мы имеем аналогичные соотношения:

di<72<7₃<74d = di<72d = — 7<7₃d;  <72<7₃d = —7<7id; d₃did = —j^a-

Отличие заключается в том, что операторы (2.4) коммутативны в псевдоскалярном пространстве. Таким образом, произвольный матричный (2 х 2)-оператор U в 7-пространстве может быть представлен, например, в таком виде:

U = рЁ - ^Адд + /zd2 + va^ -д pAjp + (A -дгуф-Р, где Е — единичная (2 X 2)-матрица, р2 + А2 + р2 + v2 = det U, а р, А, р, и — вещественные числа, описывающие связанный с 7-пространством оператор U.

Чтобы обобщить действие матричного (2 X 2)-оператора вместе с соответствующим представлением вращений на все (г, 7)-гиперпространство мы можем заменить формально комплексную единицу 7 на г в U и д^ (т. е. од -Д у):

U = рЁ - фАод + pd₂ + va^ -Д р + jp - (уА + iv^T³ •          (²-5)

Если U унимодулярная матрица и р² + А² + р² + v² = 1, то (2.5) представляет вращения в четырехмерном (г, ^-пространстве.

Перед тем, как перейти к определению полной длины в этом гиперпространстве, определим частичный детерминант в каждом из пространств-проекций:

deti а = (Reid)² + (Im_zd)² = а • а¹* = d|² = Qg + a² — a^ — a₃ + 27(0:00:2 + aia₃). (2.6)

Из правила коммутативности (1.1) и определений (2.1), (2.3), (2.6) вытекают следующие очевидные тождества:

a • b = b • а,

Re^Re^d = Не^Нещ = од = Re^d = Re^d = Red,

Im,Rejd = Rejlm,d = од,

Imjmjd = Imjlm,d = од = Im^d = Im^d = Imd,

(,й,«уз = а***³ = a*³*' = (d^)^ = a₀ - »«i - № + ija_3l              ^(2J)

a + a*¹ = 2Re^d, a — a*¹ = 2/Im,Rejd + 2j’ReJmjReid,

(d + d*^) + С.С._г = (d + d*^') + C.C.j = dRe^Re^d = 4Red, det, detj a = |d|² ^ = | d|² ^ = detj det, a.

Приведенные до сих пор правила и соотношения описывают простое скалярное объединение — суперпозицию двух полей комплексных чисел. Эти соотношения могут оказаться полезными для некоторых типичных задач за счет приведения к удобной алгебраической форме (например, в теориях волноводов [6], кильватерных полей [5], поляриметрии и аналитическом представлении магнитостатических полей [12]). Однако, чтобы построить полную алгебру гиперкомплексного пространства, она должна быть замкнута по отношению к операциям умножения и деления, возведения в степень и извлечения корня.

Для этого мы постулируем дополнительные к (1.1) правила:

Д’=Д^±1, г-гз = -з, ji-j = -i, У ;² = (Д)² = 1.          (2.8)

Остальные свойства скалярных кватернионов и соответствующие функциональные аналитические продолжения могут быть выведены из (1.1, 2.8) подобно теории обычных комплексных чисел. Например, нетрудно видеть, что:

Vu=U; VT=±1, ±у; у = ехр(±(г + Дтг/2),            (2.9)

т. е. в этой алгебре 4-го ранга квадратный корень имеет четыре значения.

Другой пример — правило умножения гиперкомплексных чисел d и 6 = /Зд + %Р\ + зф + а -Ь = «оРо + а3Рз — «1/31 — «2/32 + Цод/Зо + «оА — «зРз — од/Зз)

+ зФФо + «о/Зг — «з/31 — «1^з) + гзФзЗо + «2/З1 + «1^2 + од/Зз)-

• 3.    Сопряжение и абсолютное значение, деление и гиперполюса

Определим полное сопряжение как расширение, построенное на частичных сопряжениях:

d* = d^d^d*^'.                              (зл)

Приведем здесь дополнительно несколько полезных тождеств и неравенств для сопряженных чисел и их компонент:

d + Ф¹Ф³ + Ф"³ = 4Re_z Re^d,

а*^г*з а = ад + «1 + «2 + ^ij^a^ — одод),                  (3.2)

• d + аУ*з У 2Re а, а + а* 7^ 2Re а.

Естественный способ определить полный детерминант (определитель) через частичные детерминанты (2.6):

det а = detj detj а = | «|²1^ = аа*'а*з а*'*² = а • а*

= (оД + Ct^ — с^2 — ^з)^ + 4(ао^а2 + од од)²-                 (3-3)

Можно заметить, что определитель (3.3) может обращаться в нуль для некоторых ненулевых компонент а_п. Мы будем называть соответствующие числа полюсами (гиперполюсами или гипернулями). Мы имеем дело с таким полюсом, например, когда од = од ^ О при од = од = 0, либо когда од = од ^ 0 при од = од = 0.

В отличие от частичных детерминантов, полные детерминанты вещественны и неотрицательны. Поэтому мы определяем абсолютную величину (или норму) скалярного кватерниона через арифметический корень 4-го порядка:

\а\ = N(a) = а/ det а = а/ аа*^а*3а*¹*з = ^ а|² |².                 (3.4)

Заметим, что числа г ±7, 1±Д имеют нулевую норму (или гипердлину). Как мы увидим ниже, числа 2тг(г±7) и тг(г±7) являются гиперпериодами для гиперболических функций сН(ж), зН(ж) и Н1(ж), ctg/t(£) так же, как 2тг(1 ± Д) и тг(1 ± Д) являются гиперпериодами для тригонометрических функций соз(ж), зт(ж) и tg(i), ctg(5) соответственно.

Полный детерминант, введенный выше, можно использовать непосредственно для отыскания обратной величины гиперкомплексного числа с ненулевой нормой:

,     1 а*

а = - = -—-. a det а

Можно получить (3.5) и через последовательные преобразования в пространствах-проекциях, применяя соответствующие правила, приведенные выше:

• 1    _ а*^ ₌ а^_ ₌ а” _ У* • ^уз _ 5”УЗУ»3 _ ^

• 4.    Формула Эйлера, факторизация и извлечение корня

а а|²    Д|² а • а*^г аа*^г ■ (аа*^г)*з аа*^га*3а*^г*з й|⁴

Обращенные гипернули можно интерпретировать как гипербесконечности Д-алгебры.

Перед тем как определить извлечение корня для произвольного скалярного кватерниона рассмотрим два частных случая.

Первый случай относится к произведению двух комплексных чисел а + ib и с + jd принадлежащих к г- и 7-пространствам соответственно (см. (2.2)). Для такого гиперчисла мы имеем одод = одод, т. е. соответствующая (2 X 2)-матрица, составленная из его компонентов од, од, щ, од, вырождена.

Отметим, что этот простой случай соответствует матричному (2 X 2)-оператору (либо вращению), примененному к «плоскому» вектору (т. е. обычному комплексному числу) принадлежащему к 2-пространству (Im^ = 0). Действительно, из (3.3, 2.2) мы имеем а = у/«д + а² + «2 + «3 ⁼ Va²c² + b²c² + a²d² + b²d², а из (2.5): U —> р — iv + jp — ДА, полагая кватернион {од, щ, «2, «з} пропорциональным {р, —щ ц, —А}.

Очевидно, что в этом случае коренв n-го порядка извлекается тривиально:

Уй = V(^o + «6) • (с + jd) = уДф exp [(2 arctg 6/а + j arctg с?/с + 2?r(ti + Д))/п], (4.1)

где k, I = {0,1,... , п — 1} натуральные числа.

Таким образом, период экспоненциальной функции в нашем гиперпространстве есть 2тг(А4 + IjY В общем случае это дает п² значений для Vd.

Другой интересный случай есть гиперкомплексное число, представленное лишь двумя компонентами: А = a + ijd. Из (2.8) и разложения Тейлора можно получить основную формулу экспоненциального представления такого числа:

ехр(Д(Д = ch <р + ij sh ip.

(4-2)

При \d/a\ ^ 1 имеет место следующее представление:

А = a + ijd =

а² — d²\ exp

ij arcth — . а /

(4.3)

Заметим, что число arcth d/a вещественно при \d/a\ < 1, в противном случае оно комплексно либо в i-, либо в j-пространстве. Существует и дополнительное, «симметричное» представление в (г, Д-пространстве при \d/a\ > 1:

А = ij^d + Да) = ij а² — d²\ exp ( ij arcth - ] = а² — d²

(4-4)

(4-5)

Мы использовали в (4.4) следующее гиперкомплексное представление:

arcth ж —> — г + ? —Н arcth —, ж|>1          2          ж которое есть гиперрасширение известной формулы arctg ж = ^ sgnж — arctg Д Таким образом, область значений обратного гиперболического тангенса расширена в пространство скалярных кватернионов.

Используя (4.3) мы можем извлечь корень из простого двухкомпонентного кватерниона В = А² = b + ijc;

('"Mki + lj') 1 . /сИ

V В = \ \В\ ехр--1— г] arcth -   ,                (4.6)

v        у п п           J J где \c/b\ Д 1 и к,1 = {0,1,... , п — 1}.

Предположив, что В = А², можно провести проверочное сравнение для А = a + ijd и VH. Подставляя в (4.6) b = a² + d² и с = 2ad мы имеем:

VH = tia² — d² \ • | ch — + ii sh — |, где м = arcth |          .        (4.7)

V 2      2/               \a +d j

Простые преобразования гиперболических функций в (4.7) дают:

V^+UdV-ijj^Y             (4.8)

где различные комбинации знаков дают восемь значений для радикала. Vb. Однако только четыре из них линейно независимы в смысле (2.9), в то время как остальные получены путем умножения на. ij.

В общем случае, когда Л ^ 0, мы можем обобщить формулу Эйлера следующим образом:

А = а + ib + jc + ijd = exp(ag + газ + jap + ija^ = ехр(а),         (4.9)

где соотношение между А и а может быть найдено из системы:

{6„ = sin a, cos о, ch оз - cos о, sin о, sh 03, с, — cos 01 sinoi сЬоз — sinoi cos a, sh 03,         (4.10)

(In = sinai sin аз ch аз, где Ln = M^L cn = с/Д и (In = d,\A\ являются нормализованными компонентами.

Подобно трехмерному вращению, представленному обычным кватернионом [1], (4.9)(4.10) представляют вращение аз, аз, аз в псевдоскалярном гиперпространстве. Вырожденный случай (2.2), (4.1) можно интерпретировать по аналогии с подвесом Кардана, (когда, аз = 0 в (4.9)).

Заметим, что в отличие от обычных комплексных чисел и случаев (2.2), (2.5), (4.1), нормализованные компоненты Ln, cn, (In в общем случае могут изменяться по всей вещественной области от — оо до +оо.

Можно привести (4.10) к алгебраической системе двух неизвестных tgai и tgai:

Г tg² ai - tg² ai = (b²_N - c^) (1 + tg² ai) (1 + tg² a₂) ,               _n>

I b_N tg² ai tg ai + c_N tg ai tg² ai = d_N (tg² ai - tg² a₂)

и a3 = ln(sin(ai + a2)/(cw + b^Y                     (4-12)

Система. (4.11) может быть решена, в явном виде, однако полученные нами выражения символьными методами оказались чрезвычайно громоздкими, чтобы привести их здесь.

Чтобы обеспечить в (4.12) sin(ai + а₂)/(с^ + b^ > 0, можно всегда, выбрать подходящие решения (4.11) в виде аз ₂ + кт благодаря периодичности тангенса. При b = — с формально мы имеем особенность в (4.12). Однако эта. особенность устранима, путем комплексного сопряжения (4.9)—(4.12) (в г- или 7-пространстве) и применения сопряжения снова, (в том же пространстве) к результату, полученному в правой части.

Для извлечения корня можно предложить и другой способ разложения скалярного кватерниона. (2.2) на. сомножители:

а₀ + га_х + 703 + Да₃ = (а + гб) • (с + jd^ • (е + Д/),             (4.13)

где а, Ь, с, d, е, / вещественны. Положим в (4.13) для простоты, что ао = 1 = а = с = е. Тогда. (4.13) приводит к следующей алгебраической системе:

( a3 = bd(l-bdf) + f,

{ а₂ = dll - bdC - bL                           (4.14)

( ai = 6(1 - bdf^ - df.

Решения {6, d, /} системы (4.14) выражаются в явном виде гораздо более компактно, чем решение системы (4.11). Можно показать, что решения (4.14) существуют всегда, и они вещественны. Для одного из решений существует особенность (например, при аз + азаз = 0), которая является устранимой. Таким образом, скалярный ненулевой (|а ^ 0) кватернион представим элементарными (комплексными) сомножителями и из него можно извлечь корень в соответствии с (4.13), (4.9), либо (4.1) или (4.6).

• 5.    Обсуждение

• 6.    Благодарности

Следующими шагами в разработке скалярных кватернионов могут стать гиперкомплексные функции, их дифференцирование и интегрирование, конформные отображения и аналитические продолжения функций комплексного переменного с расширением в рассмотренное здесь гиперпространство. Мы называем это пространство псевдоскалярным, так как оно сочетает представление вращений со свойствами комплексных чисел. Поэтому можно ожидать дальнейшего развития и новых приложений этой гдалгебры, особенно в физике пучков, лазеров, плазмы, высоких энергий, а также космологии.

Автор выражает свою признательность проф. Г. В. Воскресенскому за критические обсуждения работы [10].