Компактные свойства множеств в пространстве радоновых мер
Автор: Нгуен Ван Куинь, Ле Ань Тханг
Журнал: Мировая наука @science-j
Рубрика: Естественные и технические науки
Статья в выпуске: 2 (71), 2023 года.
Бесплатный доступ
Теория меры играет важную роль в теории субгармонических и 8 -субгармонических функций. Классические свойства меры были представлены во многих монографиях, например, в [1]. В статье представляется усиление варианта Азарина теоремы об компактном множестве в пространстве радоновых мер. Результаты нашей статьи позволяют несколько упростить конструкции из этих работ.
Мера Хана, мера Жордана, сингулярная положительная мера, линейный непрерывный функционал, радоновая мера
Короткий адрес: https://sciup.org/140297887
IDR: 140297887
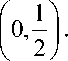
Список литературы Компактные свойства множеств в пространстве радоновых мер
- Kadets, V.M. (2006), A course of Functional Analysis, Kharkov National University.
- Van Quynh Nguyen (2015), Various Types of Convergence of Sequences of Subharmonic Functions, Zh. Mat. Fiz. Anal. Geom, Volume 11, Number 1, 6374.
- Nguyen Van Quynh, Theorem on uniform continuity of Logarithmic potential, Visnyk of science and education, Issue 5 (59), 6-10p.
- Nguyen Van Quynh, Le Anh Thang (2021), THEOREM ON THE REPRESENTATION MEASURES "Мировая наука" №3 (48) 2021.
- Nguyen Van Quynh, Le Anh Thang (2021), THEOREM ON A COMPACT SET IN THE SPACE OF RADON MEASURES "Мировая наука" №11 (56) 2021.
Статья научная
