Компартментальная модель поглощения воды корнями растения с учётом процессов на клеточном уровне

Проблема организации радиального передвижения воды и содержащихся в ней солей из внешнего раствора или почвы через неспециализированные ткани корня к сосудам ксилемы и механизмы формирования корневого давления до сих пор являются предметом обсуждения. Обсуждаемые гипотезы в основном касаются локализации активных ионных насосов в различных структурах корня, свойств клеточных мембран и сил, обеспечивающих перемещение раствора.

Одна из типичных ранних гипотез основана на представлении, что ионные насосы локализованы только в мембранах эпидермальных и гиподермальных клеток. В соответствии с этой гипотезой вода и ионы из внешней среды могут свободно проникать в апопласт (образованное межклетниками и порами клеточных стенок

пространство, которое отделено от внутриклеточного пространства – симпласта – клеточными мембранами) периферических слоев клеток. Мембраны этих клеток обеспечивают сильно увеличенную поверхность активного поглощения ионов в симпласт. Предполагается, что за этим поглощением следует пассивный симпластный транспорт к стели (слой клеток, расположенный в центральной части корня, содержащий сосуды ксилемы) и пассивное вытекание ионов в сосуды ксилемы.

Альтернативно этой гипотезе существуют и другие, касающиеся существования, локализации и мощности дополнительных механизмов активного переноса (ионов, а возможно и молекул воды) через мембраны, в частности через мембраны, разделяющие сосуды ксилемы и симпласт стели. Гипотеза об активных насосах не исключает возможности включения значительных пассивных компонентов, однако именно первым приписывается решающая роль в направленном радиальном транспорте ионов через корень. Более подробное обсуждение гипотез о возможных активных механизмах поглощения ионов и локализации ионных насосов приведено в работах [1, 2].

В экспериментах, связанных с изучением выделения ксилемного сока из срезанных корней, было обнаружено, что осмотическое давление внешнего раствора, останавливающего выделение жидкости на срезе корня, превосходит осмотическое давление ксилемного сока [3]. В связи с этим широкое распространение получило эмпирическое выражение для потока экссудата J_v .

Jv = Lp о Ac + J о, где Lp – интегральный коэффициент гидравлической проводимости, σ – коэффициент отражения, Ac - разность концентраций осмотически активных веществ внутри и снаружи корня, J 0 – так называемый неосмотический компонент потока.

Попытки интерпретировать неосмотический компонент привели к появлению компартментальных моделей, в которых различные цилиндрические слои корня рассматривались как компартменты, отделенные друг от друга и от внешней среды мембранами, зачастую с различными свойствами. При этом массообмен между компартментами описывался с помощью линейных связей потоков с перепадами гидростатического и осмотического давлений [5–8]. Подробный обзор и анализ подобных моделей приведен в [9]. Отличаясь друг от друга числом рассматриваемых компартментов и свойствами разделяющих их мембран, эти модели позволяют получать хорошее совпадение экспериментальных и теоретических зависимостей разности гидростатического и осмотического давлений между ксилемой и окружающим раствором от потока через срезанный корень. Однако подобное рассмотрение остается в достаточной мере эмпирическим и оставляет в стороне основные особенности функционирования корня как распределенной механической системы. Впервые методология континуального моделирования процессов массопереноса в корнях была предложена авторами в работе [10].

Целью настоящего исследования является построение континуальной модели, учитывающей реальное анатомическое строение корня и включающей в себя основные физические механизмы, влияющие на перенос веществ, а затем получение на ее основе более простой компартментальной модели, позволяющей оценивать участие различных предполагаемых механизмов в процессе поглощения жидкости корнем.

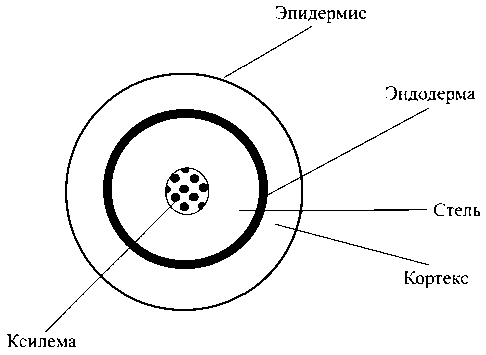
Рис. 1. Схема радиального строения корня

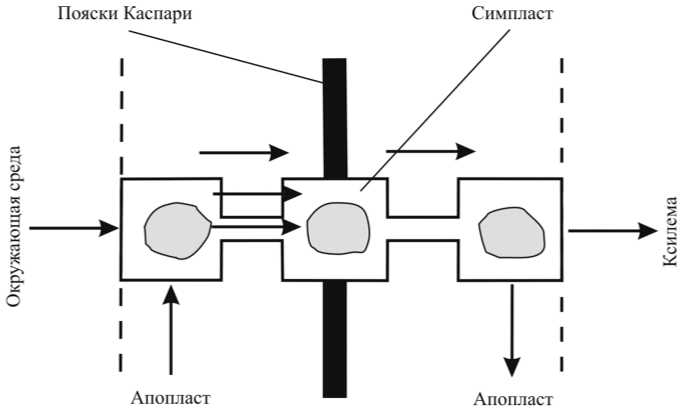
Рис. 2. Схема радиального движения жидкости в корне

К онтинуальная математическая модель

Рассмотрим основные анатомические особенности радиального строения корня растения (рис. 1). Наружный слой клеток, называемый эпидермисом, в молодых корнях специализирован как абсорбирующая ткань и обычно несет корневые волоски, значительно увеличивающие поглощающую поверхность корня. Далее вглубь выделяют слой клеток паренхимы коры, выполняющих транспортную функцию и функцию запасания веществ, а также клетки стели, отделенные от коры слоем эндодермы. Во внутренней области стели расположены проводящие элементы ксилемы, выполняющие функцию доставки воды и растворенных в ней солей в расположенные выше органы растения. Эндодермальные клетки обладают существенной особенностью в виде так называемых поясков Каспари, образованных утолщением клеточных стенок. Считается, что пояски Каспари являются непроницаемым барьером для радиального передвижения растворенных веществ и воды по клеточным стенкам и межклеточному пространству, оставляя возможность передвижения по внутриклеточному пути. Возможные пути апопластного и симпластного радиального движения воды от периферии к сосудам ксилемы представлены на рис. 2.

Предполагая осевую симметрию корня, рассмотрим его ткань как пористую сплошную среду, занимающую область r o <  r <  r i , где r o и r i - координаты границ с областью сосудов ксилемы и окружающей средой. Пористая среда заполнена двумя жидкими фазами, образованными вязкими жидкостями, находящимися соответственно во внеклеточном пространстве (апопласте) и во внутриклеточном пространстве (симпласте), и фильтрующимися через недеформируемый твердый каркас. Таким образом, в рамках макроскопической модели каждая из этих жидкостей, пространственно разделенных на микроуровне, считается заполняющей все пространство ткани. Предполагается, что в каждой фазе растворен обобщенный низкомолекулярный компонент с объемными концентрациями c ₁ и c ₂ соответственно, способный перемещаться в среде как активными механизмами переноса через мембраны, так и путем конвекции и диффузии и создающий осмотическую силу, связанную с присутствием полупроницаемых клеточных мембран. Предполагается также присутствие во внутриклеточном пространстве высокомолекулярного осмотического компонента, который не может поступать во внешнюю среду и сосуды ксилемы и распространяется из клетки в клетку за счет диффузии и конвекции по плазмодесмам. Низкомолекулярный компонент отождествляется с ионами, поглощаемыми корнем из окружающей среды, в то время как источником высокомолекулярного компонента являются сосуды флоэмы, по которым доставляются синтезируемые в листьях сахара для запасания в корнях.

Будем считать, что поток жидкости между симпластом и апопластом осуществляется за счет перепадов осмотических и гидростатических давлений. Считая концентрации малыми, запишем законы сохранения массы для фаз в виде

1 д vr   т      1 д v7r pi--— = J, Р 2--—=-J, r д r           r д r                                       (1)

J = Lp [p2 - pi + RT(ci - c2 )-пimp], где Pi и p2 - объемные плотности фаз, vi и v2 - скорости жидкости в апопласте и симпласте соответственно, p1 и p2 – гидростатические давления в апопласте и симпласте, Lp – коэффициент гидравлической проводимости, J – межфазный поток жидкости, T- абсолютная температура, R = p 0 R0 /ц 0 (R0 - универсальная газовая постоянная, ц0 - эффективная молярная масса растворенного низкомолекулярного компонента, р0 - плотность воды), пimp - осмотическое давление, создаваемое высокомолекулярным компонентом, растворенным в симпластной фазе. В качестве коэффициента отражения для обоих учитываемых компонентов взята единица, что соответствует невозможности их конвективного переноса через мембраны.

Важной особенностью модели является описание движения жидкости во внутриклеточном пространстве, учитывающее движение воды и растворенных в ней веществ через периодические структуры, образованные внутриклеточными объемами, клеточными мембранами и стенками, перфорированными канальцами (плазмодесмами), которые соединяют цитоплазматические объемы соседних клеток. Для описания переноса в такой среде рассмотрим движение в одиночной структурной клеточной ячейке, представленной на рис. 3. Интегрирование уравнения движения жидкости в форме закона фильтрации в пористой среде (с учетом распределенной осмотической силы) по длине области, занимаемой внутренним содержимым клетки, и по удвоенной толщине клеточной стенки позволяет заменить эти области

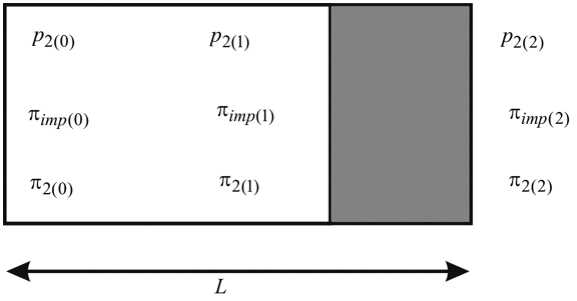
Рис. 3. Схема клеточной ячейки. Светлым выделено пространство внутри клетки, темным – разделяющая две соседние клетки структура, образованная мембранами и стенками обеих клеток обобщенными мембранами с коэффициентами отражения меньшими единицы и написать соотношения между потоком жидкости Jw = v 2 и перепадами гидростатического и осмотического давлений вдоль соответствующих частей структурной клеточной ячейки в виде

J w = ^k 1 [ ^p 2(0) - ^p 2(1) + ° 1 ^(п 2(1) - ^п 2(0) ^)+о 01 ^(п imp (1) ^-п imp (0) ) ] , J w = ^k 2 ^{[ p} 2(1) ^{- p} 2(2) ⁺ ° 2 ⁽ⁿ 2(2) ^-n 2(1) ⁾⁺ ° 02 ⁽ⁿ imp (2) ^-n imp (1) ^)] -

Здесь k i ( i = 1, 2) - коэффициенты гидравлической проводимости соответствующих частей ячейки, а о i и о 0 i - коэффициенты отражения для низко- и высокомолекулярного компонентов во внутриклеточной части ячейки и клеточной стенке соответственно. Считается, что осмотические давления и концентрации связаны между собой стандартным соотношением для идеальных растворов.

Выделив в отдельную составляющую растворенные в симпласте низкомолекулярные вещества, напишем для них закон движения в форме квазистатического условия равновесия.

Rc + Rs + Rf = 0, где Rc – сила, действующая на растворенный компонент за счет перепада химического потенциала, Rs и R f – силы взаимодействия между растворенным веществом и твердой фазой, к которой относится как клеточная стенка, так и внутриклеточные структуры, и между растворенным веществом и водой соответственно. Для введенных сил приняты следующие зависимости [4]:

du

R = — k     , R_s = — k_svо , R г = — k г ( v„ — v t ).

c c d s s s /              s 2

Здесь vs – скорость движения растворенного вещества, µ – химический потенциал растворенного вещества, для которого в данном случае может быть принята простейшая логарифмическая зависимость от концентрации. Тогда выражение для потока растворенного низкомолекулярного вещества Js = c2 vs получим в следующем виде:

J

s

kc p0(ks + kf )

dCt RT -2- + dr

kf ks + kf

c 2 ^Jw ^.

После интегрирования этого соотношения по различным частям клеточной структурной ячейки и введения коэффициентов, традиционных для описания потоков через мембраны, получим

J s ^- -® (1) ^{( c} 2(0) ^{- c} 2(1) ^{) +} ( 1 ^- ° 1 ) ^c 2(1) J w , J s ^{- -ю} (2) ^{( c} 2(1) ^{- c} 2(2) ^{) +} ( 1 ^- ° 2 ) c 2(2) J w •

Здесь Го ( i ) ( i - 1,2) - коэффициенты проницаемости внутриклеточной и внеклеточной частей структурной ячейки по отношению к растворенному компоненту, c ₂ ( _i ) ( i - 1,2) - средняя концентрация по соответствующей части ячейки.

Проведя осреднение по малому объему среды, содержащему достаточно много структурных ячеек, получим

Jw - р| - ^2 + °1 V1 + °2 V2 + °0191 + °0292 'I,(2)

V dr)

Js - -®1 V- + (1 - °1)c2(1) Jw ,

ГТ ■

Js --ю2 V2 + (1 -° 2 )c 2(2) Jw •

ГТ ■

Макроскопические коэффициенты гидравлической проводимости β и проницаемости по отношению к растворенному веществу Го 1 и го 2 выражаются через клеточные параметры следующим образом:

в-

( 1     1 I

-1

— + —

V I ^Л2 у

L ,

Го 1 - Го (1) L ,    Го 2 - Го (2) L ,

где L – длина клеточной ячейки.

Величины V 1 ^и V 2 , 9 1 ^и внутриклеточному пространству и

9 2

в

осреднения слагаемых ( п 2(1) -п 2(0))/ L и ( п 2(2)

характеризуют изменение концентрации по клеточной стенке и являются результатом

^п 2(1) V L , ^(п imp (1)

^п imp (0))/ L ^и

( п imp (2) -п imp (1))/ L • Изменение концентрации в симпласте в целом связано с

изменениями концентрации по различным частям клеточной ячейки посредством соотношений

дпт           _ _

V 1 +V 2 ^- "^, ^п 2 ^{- c} 2 ^RT • о r

Концентрация в симпласте c ₂ является средней концентрацией по длине клеточной ячейки и связана со средними концентрациями по различным частям ячейки c ₂₍₁₎ и c ₂₍₂₎ следующими приближенными соотношениями:

c 2(1) = c 2

^(у 1 + У 2 ) L 2

2 RT

c 2(2) = c 2 +

⁽ У 1 + У 2 ) L 1

2 RT

выполняющимися точно в случае линейного распределения концентрации по частям ячейки.

Приравнивая правые части выражений (3) и (4), учитывая (5), (6) и пренебрегая нелинейными слагаемыми, имеющими форму произведения скорости жидкости на производную концентрации, получим

RT L d c 2 . / A ) ^у 1 =--------- 1 ® 2 _ ¹ (^y 2 ^-a 1 ) c 2 v 2 I ,

O>1 + Ж ydr           )

У 2 =

RT

Ш 1 + ^ 2

(   d c2 /

^1.  1(0

y   о r

^-G 1 ) c 2 v 2

Рассмотрение потоков высокомолекулярного вещества в различных частях клеточной ячейки с последующим их осреднением по объему среды приводит к написанию выражений для потока растворенного высокомолекулярного вещества Ic , аналогичных (3) и (4). Тогда выражения для величин ф1 и ф2, характеризующих изменение концентрации высокомолекулярного вещества во внутриклеточном пространстве и клеточной стенке, могут быть получены в виде

Ф 1 =

RT (а ^d c imp / а , а ⁶ 2   --- ^{+ (с} 02

)

-° 01 ) c imp v 2

)

61 + 62 (     оr ф 2 =

RT Га ^d c imp / а , а ⁶ 1    --- ^{+ (с} 02

61 + 6₂ (     о r

)

-^ 01 ) c imp v 2

)

Здесь 6 1 и 6 2 - коэффициенты проницаемости соответствующих частей клеточной ячейки по отношению к растворенному высокомолекулярному веществу.

Подстановка у i и ф i ( i = 1, 2) в соотношения (2)-(4) и аналогичные соотношения для высокомолекулярного вещества даёт выражения для потоков J_w , J_c и I_c :

v 2 =Р 2 ^{( с} 2 ) ^--p 2 ⁺ ^ ^RT -r^" ⁺ S1 RT

^ c imp d r ₎

,

d c^

Jc = ^- D 2      ^{+( 1} -G ) c 2 v 2 ,                              ⁽⁸⁾

d r

Ic = -D imp + (1 - G1 ) cimp v2 , dr             r где эффективная проводимость симпласта 02 (c2), эффективные коэффициенты диффузии низкомолекулярных и высокомолекулярных веществ D2 и D, а также коэффициенты g и G1 выражаются через характеристики клеточной ячейки следующим образом:

Р 2 ^{( c} 2 ^)-

___________________________Р____________________________

1 + Р RT (( _{Ю 1} +_{Ю 1}) Чо -_{О 1}) ² c 2 + ( 0 1 +0 1 ) ^{- 1} (1 о о ) ² C imp/

( 1       1 А-1

D 2 - — + —

<®1 ®2V

,

( i i А-1

D- г+г •

V01   02 V

а> 1 ^а 2 +Ю 2 ^а 1         ⁰ 1 ^а 02 + ⁰ 2 ° 01

5 ---------------• ^ 1 -----а---а-----

Ю 1 + ® 2               0 1 + 0 2

.

При написании динамического уравнения, описывающего движение жидкости в апопласте, пренебрегая осмотической силой, уравнение движения примем в виде закона фильтрации

V1 --₽, >• о r

где Р 1 является коэффициентом фильтрации жидкости в апопласте.

Описание баланса массы растворенных в апопласте и симпласте веществ учитывает диффузионное и конвективное распространение вещества, а также пассивный (диффузионный) и активный массообмен между фазами. При описании массообмена между симпластом и апопластом пренебрегаем конвективным переносом вещества, считая клеточную мембрану идеальной (при этом о 2 может, вообще говоря, существенно отличаться от единицы, так как внутриклеточные пространства сообщаются между собой посредством плазмодесм). Тогда с учетом (8) и (9) уравнения баланса массы примут вид

( dci 1 dcvir P11 1 +

V d t r d r

- к + X ( c 2 ^- c 1 ^)+p 1 D1- — r d r

( r ^ а , V d r J

( ^{d c} 2 + 1 ^{d( 1} -; ) ^c 2 ^v 2 ^r '

V d t r      d r      _v

1 d ( dCt А

^{- k -} X ⁽ c 2 ^{- C} 1 ^)+p 2 D 2- — I ^r -— I •          ⁽¹²⁾

r dr V dr V

p ₂

^d c imp + ^{1 d( 1} ^ 1 ) c imp v ^{2 r} _v d t     r        d r         _v

/

-P 2 D1   r r dr

V

^ c imp d r J

.

Здесь k – межфазный активный поток вещества, λ – проницаемость клеточных мембран по отношению к растворенному веществу, D 1 – коэффициент диффузии растворенных в апопласте веществ.

Уравнения (1), (7), (10)–(13) образуют замкнутую систему для нахождения величин v ₁ , v ₂ , p ₁ , p ₂ , c ₁ , c ₂ , c_imp и позволяют рассматривать различные постановки задач путем выбора соответствующих граничных условий и усложнения вида коэффициентов.

Эксперименты по изучению поглощения раствора из окружающей среды, проводимые над срезанными корнями, показали способность корней длительное время поддерживать стационарный расход жидкости на срезе. В связи с этим далее будет рассмотрена постановка задачи об осесимметричном стационарном течении жидкости из внешней среды во внутреннюю емкость, отождествляемую с сосудами ксилемы.

Будем предполагать, что концентрация внешнего раствора, а также давления во внешнем растворе и сосудах ксилемы являются данными фиксированными величинами (при этом будем пренебрегать пограничным диффузионным слоем на поверхности корня и считать концентрацию на поверхности равной концентрации в окружающей среде), в то время как концентрация в сосудах ксилемы подлежит определению наряду со скоростью поступлению жидкости в нее.

Учитывая, что внешний раствор имеет непосредственный контакт с апопластом, а поступление жидкости и растворенных веществ в симпласт осуществляется путем переноса через клеточные мембраны, на внешней границе корня поставим следующие условия:

r = r1 : P1 = Pe, c1 = ce, p2v2 = Lpe [(p2 - pe ) + RT(ce - c2 )-nimp ],

( 1 -_? 1 ) C imp V 2 — D ^ = 0,                              (14)

r        о r p 21(1 -s) c 2 v 2 - D2 2| = -ke + X e (c 2 - Ce). к                 drу

Условие на внутренней границе r = ry, соответствующей границе раздела ткани корня и ксилемы, описывающее свободное вытекание раствора из апопласта в ксилему, связано со структурой течения жидкости в самих сосудах. Если предположить, что раствор по всей границе сосуда ксилемы поступает с одинаковой концентрацией, то (при естественных условиях на концентрацию на его торцах) концентрация внутри сосуда будет постоянной (не зависящей от радиальной и осевой координат). Учитывая условия непрерывности концентрации, скорости раствора, а также потока вещества на границе раздела с сосудами ксилемы, получаем граничное условие, соответствующее принятому в традиционных компартментальных моделях условию конвективного уноса растворенного вещества на границе с ксилемой [9], r = r0 : ^c1 = 0.                                  (15)

о r

Следует еще добавить условия, описывающие возможное пассивное перетекание воды из симпласта в ксилему через разделяющие их мембраны и клеточные стенки, а также активный и пассивный перенос растворенного вещества из симпласта в ксилему.

r = r0 : Pl = Px, p2v2 = Lpx [(px - p2 ) + RT(c2 - cx )+ nimp ],

( 1 -s i ) C imp v 2 - D^ = 0,                                ⁽¹⁶⁾

о r p 21(1 - s) c2 v2 - D2 ^Cr | = -kx + X x (Cx - c2 )• к                 dr у

Здесь давление в ксилеме p_x , равно как и характеристики мембран, отделяющих клетки от сосудов ксилемы, считаются постоянными.

Дополнительно в месте расположения поясков Каспари ( r = r_c ) поставим условия непроницаемости для течения раствора в апопласте

5 c + r = rc : v+= V1 = 0,       =     = 0(17)

drd и условия непрерывности для p2 , c2 , cimp , v2 и диффузионных потоков в симпласте f a                                   дcl    дcimP \ ы

(последнее сводится к непрерывности —— и ----). Индексы « + » и « — » показывают ar      д r значения величин по разные стороны от r = rc.

Далее предполагается, что все коэффициенты за исключением параметров k и λ, характеризующих межфазный массобмен растворенным в фазах веществом, являются постоянными. Будем также пренебрегать потоком воды и растворенных веществ через внешнюю и внутреннюю границы симпласта по сравнению с потоками между симпластом и апопластом. В этом случае условия на потоки воды и растворенных веществ превращаются в условия непротекания л д c2       д cimP v2 = 0, ---= 0, -----= 0 при r = r0 и r = r.              (18)

"        д r          д r                   ^и

Структура уравнений и граничных условий такова, что позволяет в дальнейшем везде кроме уравнения (7) исключить п imp путем замены p 2 на p 2 — п imp . Оценки, выполненные для коэффициента с^, показывают, что он близок к единице. Если отличием его от единицы пренебречь, можно исключить концентрацию высокомолекулярных веществ из рассмотрения. При этом становится ясно, что осмотически активное вещество, не переносимое потоком через мембраны, не оказывает влияния на распределение скоростей и концентраций, а тем самым и на перенос воды и растворенных в ней ионов из почвы в сосуды ксилемы. В настоящей работе оно не рассматривается.

О средненные соотношения и расчеты

Перейдем от дифференциальных уравнений к интегральным соотношениям путем введения средних величин по соответствующим областям. Для произвольной функции f ( r ) введем следующие средние значения:

r1

• <    f >+ = 2Jrf (r)dr/(r2 — r2), < f >— = 2 Jrf (r)dr/(rc — r2).(19)

rcr

Дополнительные соотношения между введенными средними величинами и значениями функций на концах интервалов интегрирования, являющиеся точными при линейном распределении по переменной r функции r f ( r ) , примем в виде

• <    f > + = f l ^r 1 ^{+ f}c^rc   <  f > — = ^fc^rc ⁺ f 0 ^r 0

• ^r 1 ^{+ r}c   ’                 ^rc ^{+ r} 0    "

Примем также, что <  v 2 /Р2 ( c 2 ) > ± =< v 2 > ±/ p 2 ( < c 2 > ± ).

Для получения соотношений между средними по соответствующим областям величинами проинтегрируем по областям [ r o , r_c ] и [ r c , r 1 ] умноженное на r второе уравнение (1), умноженные на r ² уравнения (7), (10) и умноженное на r уравнение (12), записанное в стационарном виде, используя при этом приближенные равенства (19) и граничные условия (14)-(18). Уравнение (11) интегрируется по области [ r o , r_c ] .

Интегрирование уравнения сохранения массы для корня в целом в пределах [ r o , r_c ] и [ r_c , r 1 ] с учетом граничных условий и соотношений (19) дает связь между средними скоростями в симпласте и апопласте

Р1 < V1 > = р 2 < v 2 > , Р1 < V1 > = р 2 < v 2 >

Введем обозначения р 2 v 2 Г_ _ r _—р 0 v и <  P i > ± _ P i± ,    <  p 2 > ± _ p 2± ,

±    ±

< с 2 > _ с 2 . Используя дополнительные соотношения между средними величинами и значениями функций на концах интервалов интегрирования (19), получим, что

+ v ² r r _ r_c         ^r_c ро            - v ² r r _ r_c         ^r_c р₀

< v 2 >+_------c- _- v c 1-0_, < v 2 > _------c_ _- v c r0.

• ^r 1 ^{+ r}c       ^r 1 ^{+ r}c р 2                ^r 0 ^{+ r}c       ^r0 ^{+ r}c р 2

Соотношения (20) приводят к равенствам

< vi >+

^rc   р 0

^r 1 ^{+ r}c р 1 ’

< vi >

r_c   р ₀

r ₀ + r_c р ₁

Примем следующие дополнительные гипотезы:

< c i >^{+ _ c}e ’ <  c i > ^{_ c}x ’ ^c 2| _r _ _r c = 2^{( c} 2 ^{+ c} 2 ) ’

-       -     - d c_?        c + + - c —

< c i v i > _< c i > <  v i >  ’ —2      _ 2—--- 2 .

^{d r}r _ r_c      ^r i ^{— r} 0

В результате получим замкнутую систему алгебраических уравнений

+    — „+    — „+ — относительно неизвестных p1 , p1 , p2 , p2 , c2 , c2 , v, cx .

Y i ^{v _} P i ^{+ —} P 2 ⁺ X ^{( c} 2 ^{— c}e ) ’

Y 2 ^{v _} P 2 ^— P i- ⁺ X ⁽ c x ^{— c} 2 ) ’

R i^{v _} P e ^— P i ⁺ ,

R 2 ^{v _} P i- ^- P x ’

R 0 ^{v _ P} 2 ^{- P} 2 ⁺ X i ^{( c} 2 ^- c 2 ^

— k —X ( c^ — c_Y ) ⁼ a c_vv .

xx

Здесь использованы следующие обозначения:

Yi _

2 r c

L P ^{( r} i^{2 — r}c ²⁾

р 0 ’

Y 2 _

2 r c

L P ^{( r}c ^{2 — r} 0²⁾

р 0 ’

X_ RT ’ X i _? RT ’

R 0 - R 0i ⁺ R 02 ’

R 0i ^_

i р 0 ^{( r} i ^{— r}c ) ^rc

² р 2 ^{( r} i + ^rc ) P ( c 2 )’

_D _ ⁱ р0^{( r}c ^{— r} 0 ) ^rc

R 02 ^_p; —7—:—7 t^-”’

² р 2 ^{( r}c + ^r 0 ) P ( c — )

i р 0 ^{( r} i ^{— r}c ) ^rc 2 р1 ( r i + r c ) P i

R _ 1 р 0 (rc —r0) rc а_р0rc’  9_р0rc (1 — ?),

• ²    2 р 1 ( r c + r 0 ) P i

k - = ¹ ( C - r ₀ ² ) < k >^- , k ⁺ = ¹ ( r ₁ ² - r_c ²) < k >⁺ , D = D2^^ , ^{2                        2                            r} 1 ^{- r}0

• X^- = 2 ( r_c ² - r ₀ ² ) < X >^- , X⁺ = 2 ( r ₁ ² - r_c ²) < X >⁺ .

Система алгебраических уравнений, аналогичных приведенным, может быть получена в рамках компартментального описания процессов переноса в корне путем введения четырех компартментов, соответствующих внешней и внутренней (по отношению к пояскам Каспари) областям симпластного и апопластного пространств. Тогда первые два уравнения описывают обмен жидкостью между симпластом и апопластом. Следующие три уравнения являются законами движения жидкости во внешней и внутренней областях апопласта и в симпласте. И, наконец, последние три уравнения описывают массообмен растворенного компонента во внешней и внутренней областях корня между симпластом, апопластом и сосудами ксилемы. В отличие от предшествующих компартментальных моделей транспорта жидкости в корнях, в предлагаемых уравнениях коэффициенты не являются полностью эмпирическими, а определяются на основе данных о клеточных параметрах и параметрах анатомического строения.

Заметим, что при осреднении учтено, что параметры λ и k различаются во внешней и внутренней областях. Это различие принципиально для анализа эффективности рассматриваемого механизма массопереноса.

Интересующие нас зависимости концентрации в ксилеме c_x и разности давлений между окружающей средой и ксилемой A p = p e - p x от скорости вытекания жидкости через срез корня получаются в виде следующих алгебраических соотношений:

cx

0,5 d ( c e + k ⁺Д⁺ + k ^-Д^- ) v + D ( c_ek +^ X + - k ~Д~ ) 0,5 9a (V X⁺ - V X^- ) v ² + ( a + D a (l/ X⁺ + V X^- ) - 0,5 d ) v + D ’

^A p = Rv ^{+ (} X ^- X 1 ^{) (} c 2 ^- c + ^{) +} X ⁽ C e ^- C x ), R = R 0 ⁺ R l ⁺ R 2 +Y 1 +Y 2 ,

-

c ₂ = c_x

P   ' v 1

V X J

k + ,

X-

a

= -   cxv ++

X+X

Сравнение теоретических результатов с результатами, полученными экспериментально в работе [6], проводилось при следующих значениях параметров: r₀ = 0,5 мм, r 1 = 0,1 мм, r_c = 0,35 мм, n _ext = 0,15 МПа, c 1 = 0,3, c ₂ = 0,9, q= 0,8999,

P l /p c = 0,07,        P 2/pa = 0,63,

L p = 4,2 -10 -5 ^г---, м ³ - с - Па

D 1 = 3 - 10 "¹⁰ — , с

D ₂ = 2,1 - 10 ^{- 14} — , ⁺= 0,058 -кг-, с                      м ³ - с

- = 0,047 -кг-, <  k >⁺= 1,25 - 10 ⁴ -кгм ³ - с                         м ³ - с

• -       ,^-9 кг             ,^-17 м               ,^-17 м

• < k > = 6,25 - 10 —z—, Р] = 0,4 - 10   -----, Р₂ = 1,5 - 10   —

_м ³ _{- с}                     с - Па                     с -1

Результаты сравнения приведены на рис. 4 и 5.

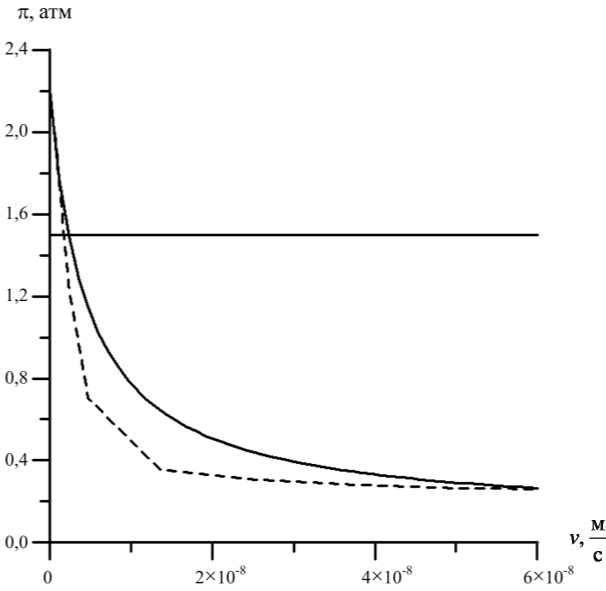
Рис. 4. Графики зависимости осмотического давления в ксилеме от скорости потока на срезе корня (пунктирная линия соответствует экспериментальным данным, сплошная – расчетам на основе модели, горизонтальная линия – осмотическое давление в окружающей среде)

м

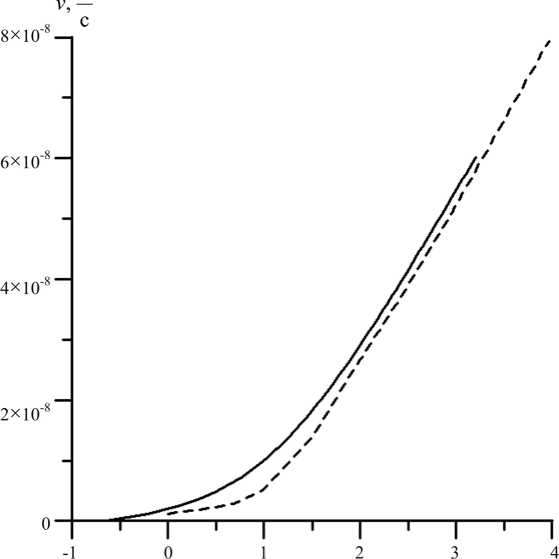
Рис. 5. Графики зависимости скорости потока на срезе корня от разности гидростатических давлений между окружающей средой и ксилемой (пунктирная линия соответствует экспериментальным данным, сплошная – расчетам на основе модели)

З аключение

Предложенная и обоснованная компартментальная модель позволила проанализировать участие основных известных механизмов в процессе поглощения воды и растворенных в ней веществ корнем растения. Результаты расчетов показывают достаточность существования активных насосов только в периферических слоях клеток для создания наблюдаемых в эксперименте потоков жидкости и концентраций на срезе корня. В дальнейшем будут проведены вычисления по более полной (континуальной) модели, которые необходимы как для проверки полученных на компартментальной модели результатов, так и для ее возможного уточнения. В свою очередь, континуальная модель может быть в случае необходимости модифицирована с учетом дополнительных возможных механизмов.

Работа поддержана РФФИ (проект № 08–01–00492) и Государственной программой поддержки ведущих научных школ (проект № НШ–1792.2008.1).