Компартментальное моделирование транспортных процессов в корне растения, учитывающее присутствие пограничных слоев
Автор: Логвенков С.А., Штейн А.А.
Журнал: Российский журнал биомеханики @journal-biomech
Статья в выпуске: 4 (62) т.17, 2013 года.
Бесплатный доступ
На основе информации о структуре решения и асимптотических оценок в задаче о стационарном потоке через корень получена система приближенных алгебраических соотношений, аналогичная имеющимся компартментальным моделям. Предлагаемый метод имеет по сравнению с последними существенное преимущество, позволяя учитывать особенности анатомического строения корня и неоднородность распределения величин по его сечению. Это дает возможность сформулировать простые конечные зависимости, совпадающие с достаточной точностью с численным решением, получаемым в рамках континуальной модели. Применение предлагаемого подхода для решения конкретных задач оказывается более простым по сравнению как с численным решением, основывающимся на континуальной модели, так и с решением, получаемым асимптотическими методами.
Поглощение воды растениями, корень растения, многофазные среды, клеточные системы, транспортные процессы, клеточные мембраны, компартментальные модели
Короткий адрес: https://sciup.org/146216114
IDR: 146216114 | УДК: 531/534:[57+61]
Текст научной статьи Компартментальное моделирование транспортных процессов в корне растения, учитывающее присутствие пограничных слоев
Изучение механизмов, участвующих в переносе веществ в корнях растений и обеспечивающих поддержание корневого давления для подъема воды на необходимую высоту и снабжение растения питательными веществами, поступившими из почвы или окружающего раствора, оказывается невозможным без использования математических моделей.
По большей части для этой цели используются компартментальные модели, в которых различные цилиндрические слои корня рассматриваются как компартменты, отделенные друг от друга и от внешней среды мембранами, вообще говоря, с различными свойствами. При этом массообмен между компартментами описывается в рамках традиционных для неравновесной термодинамики линейных связей потоков с гидростатическими и осмотическими давлениями. Компартментальные модели, предложенные в работах [5–9], отличаясь друг от друга числом рассматриваемых компартментов и свойствами разделяющих их мембран, позволили находить хорошее совпадение с получаемыми в эксперименте зависимостями, в частности с зависимостью разности гидростатических давлений между ксилемой и окружающим раствором от потока через корень. Однако подобное рассмотрение остается в достаточной мере
Штейн Александр Александрович, к.ф.-м.н., ведущий научный сотрудник Института механики, Москва эмпирическим и оставляет в стороне основные особенности функционирования корня как распределенной механической системы. Вследствие этого модели такого рода неизбежно остаются привязанными к узкому кругу экспериментов и частных гипотез и мало пригодны для включения в полную гидромеханическую модель транспорта в растениях.
Недостатки компартментального моделирования привели к необходимости рассматривать более полные континуальные модели, учитывающие реальное анатомическое строение корня и включающие в себя основные физические механизмы, влияющие на перенос веществ [1, 2, 10]. Однако решение задач на основе континуальных моделей существенно сложнее, чем на основе компартментального моделирования. Последовательное использование асимптотических методов [4] оказалось громоздким и реализуемо лишь в очень простых случаях, охватывающих малую часть подлежащих решению задач.
В работе [1] авторами была получена компартментальная модель, основывающаяся не на схематическом представлении корня совокупностью мембран, а на осреднении континуальных уравнений раздельно в двух областях, граница между которыми задается областью поясков Каспари. Однако в каждой из этих областей осреднение по пространственной координате выполнялось стандартным методом, дающим хорошие результаты для гладких функций. Между тем, как показало численное решение [1, 10], в каждой из этих областей имеются пограничные слои, в которых осредняемые функции резко меняются, что может внести существенную погрешность в результаты, полученные методом осреднения, использованным в исследовании [1].
В предлагаемой работе на основе асимптотических оценок выведены уточненные осредненные соотношения, учитывающие информацию о структуре решения в задаче о стационарном потоке через корень, полученную на основе континуальной модели [1, 10]. Получены приближенные формулы, описывающие зависимость потока жидкости через корень от разности приложенных давлений и концентрации низкомолекулярного компонента от потока жидкости, а также распределение давлений, скоростей и концентраций по сечению корня.
Задача о стационарном потоке веществ через корень растения. Континуальная модель
Методология континуального моделирования процессов массопереноса в корнях впервые предложена авторами в работах [1, 10]. В этих работах была разработана базовая континуальная модель, учитывающая реальное анатомическое строение корня, включающая в себя основные физические механизмы, влияющие на перенос веществ и позволяющая оценивать участие различных известных и предполагаемых механизмов в процессе поглощения жидкости корнем. Ткань корня моделируется жидким континуумом, заполняющим пористый каркас и состоящим из двух фаз, соответствующих внутриклеточной (симпласт) и внеклеточной (апопласт) жидкостям. Система уравнений и граничных условий подробно описана, например, в работе [1] и приводится здесь для случая стационарного осесимметричного течения без каких-либо обоснований и объяснений.
В предположении осевой симметрии корня решение ищется в области r 0 ≤ r ≤ r 1, где r 0 и r 1 – координаты раздела корня с сосудами ксилемы с окружающей средой. Стационарные распределенные уравнения имеют следующий вид:
1 dv r ρ 1 1
rdr
= J ,
р21 dvr = - J, J = Lp [ P 2 - P1 + RT (c - c 2)],(2)
rdr
V —ft dp",(3)
dr
-
V2 =₽2 (-dp2+6 RTdc2 ).(4)
^ dr dr j
-
1 dcvr , „, . 1 d ( dc )
Pi= -k + X(c2 -ci) + PiD , r77 ,(5)
-
r dr r dr ^ dr J
1 d (1 - c ) cvr , „ , . 1 d ( dc )
P 2 , 2 2 = k -X ( c 2 - c 1 ) + P 2 D 2-— r77- ■ (6) r dr r dr ^ dr J
Здесь индексы 1 и 2 соответствуют внеклеточной и внутриклеточной фазам соответственно; р 1 и р 2 - объемные плотности фаз; v 1 и v 2 - скорости жидкости в апопласте и симпласте; J – межфазный поток жидкости; L p – объемный коэффициент гидравлической проводимости ткани; p 1 и p 2 – гидростатические давления в фазах; R = p 0 • R 0 /р0 ( R 0 - универсальная газовая постоянная, p 0 - молярная масса растворенного низкомолекулярного компонента, р 0 - плотность воды); T - абсолютная температура; c 1 и c 2 – массовые концентрации обобщенного низкомолекулярного компонента в каждой фазе; |к и в 2 - проводимости апопласта и симпласта; 6 - распределенный коэффициент отражения симпласта; к - межфазный активный поток вещества; X - проницаемость клеточных мембран по отношению к растворенному веществу; D 1 и D 2 – коэффициенты диффузии растворенных в апопласте и симпласте веществ. Коэффициенты системы (1)–(6) в дальнейшем предполагаются постоянными за исключением X и к , которые считаются кусочнопостоянными с разрывом в месте расположения поясков Каспари, соответствующем r = rc ( r 0 < rc < r 1 ): при r > rc X = X+ , к = к + , при r < rc X = X- , к = к - .
Предполагается, что концентрация внешнего раствора, а также давления во внешнем растворе и сосудах ксилемы являются известными фиксированными величинами, в то время как концентрация в сосудах ксилемы подлежит определению наряду со скоростью поступления жидкости в нее.
Система граничных условий в пренебрежении потоком воды и растворенных веществ через внешнюю и внутреннюю границы симпласта по сравнению с потоками между симпластом и апопластом следующая (верхние индексы + и - соответствуют значениям функций по разные стороны от границы, определяющей пояски Каспари r = rc ):
dc r = r1: Р1 = Pe. c1 = ce. V2 = 0. -Г = 0. dr r = ro :
dc 1 = 0, v 2 = 0, dc 2 = 0, dr dr
de+ de r = rc:
V + = V - = 0, dc ^ = dc ^ = 0.
-
1 1 dr dr
Приближенные формулы
Решение поставленной выше задачи при значениях коэффициентов, приведенных ниже, показало, что величины c 2 , p 2 , rv 1 и rv 2 испытывают значительные изменения в пограничных слоях, примыкающих к внешней и внутренней границам поперечного сечения корня, а также слева и справа от поясков Каспари. Толщины пограничных слоев различаются для различных функций. Так, толщины пограничных слоев для концентрации в симпласте в зависимости от их локализации имеют величины порядка D 2 /v* и ^р2 D 2 /X. ( v * и X * - характерные значения скорости и проницаемости клеточных мембран по отношению к растворенному веществу), а для давления в симпласте и скоростей - порядка ^р2 Р 2/ L p [3]-При выбранных значениях коэффициентов функции c 1 и p 1 не испытывают резких изменений типа пограничного слоя. В области сечения, исключающей пограничные слои, величины rv 1 , rv 2 , c 1 и c 2 меняются слабо. К этим заключениям можно прийти и на основании более подробного асимптотического анализа. Перечисленные факты отражены на рис. 1. Заштрихованные области включают пограничные слои для всех величин, а буквенные обозначения соответствуют значениям функций на границе с пограничным слоем или значениям во всей области для слабо меняющихся величин.
Проинтегрируем уравнения (3) и (4) по интервалам, получаемым исключением из отрезков [ r 0 ; rc ] и [ rc ; r 1] заштрихованных на рис. 1 областей, содержащих пограничные слои. Учитывая, что величины u 1 = - rv 1 , u 2 = - rv 2 и c 2 в каждой из областей практически постоянны, а также пренебрегая толщиной переходных слоев, получим приближенные равенства
= — In
P i
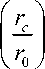
u 1,
*
P i - P.
**
p 0 - P i
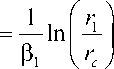
U1+ rc
* 1
*
u 2 ,
+ ** 1 i
P 2 - P 2 = |П
P 2
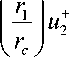
* -
P 2 - P 2 = T^ln r 2
В этих областях уравнение (1) принимает простой вид p 2 - P 1 + RT ( c 1 - c 2) = 0. Тогда значения величин на границах переходных областей оказываются связанными между собой соотношениями
P 2 - Px + RT ( c x - С 2 ) = 0, P * - P i* + RT ( c x - c 2 ) = 0, P 2* - p ** + rt ( c 0 - c + ) = 0, P 2 +- P 0 + RT ( c 0 - c 2 + ) = 0-
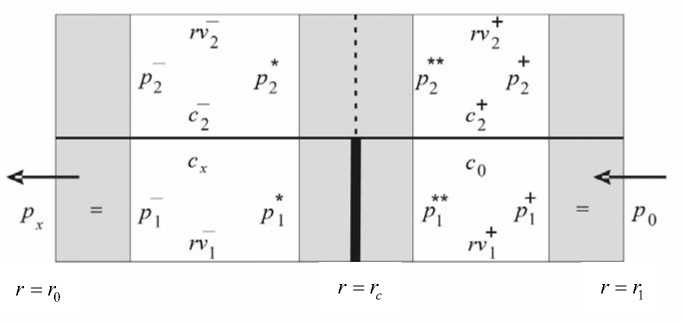
Рис. 1. Расположение пограничных слоев для концентраций, давлений и скоростей (заштрихованные области); буквенные обозначения дают значения соответствующих функций на границе с пограничным слоем или значения во всей области для слабо меняющихся величин
Значения числовых параметров: L p = 4,2 - 10 6 кым 3 -с 1 -Па 1 ; п ext = 0,15 МПа; с; = 0,89; r 1 = 0,5 мм; r 0 = 0,1 мм; r c = 0,35 мм; р 1 /р0 = 0,07; р 2 /р 0 = 0,2; к + = 6,2 - 10 - 5 кгм -3^-1 ; к - = - 6,2 - 10 - 9 кгм -3^-1 ; Х+ = 1,4 - 10 - 2 ктм "3^"1 ;
-
X- = 2,1 - 10 - 3 кг-м —3 -с —1 ; D 1 = 3 - 10 - 10 м 2 -с -1 ; D 2 = 5 -Ю"15 м2< 1 ; р 1 = 8 - 10 - 18 м 2 -Па "1 -с" 1 ; Р 2 = 4 - 10 - 18 м 2 -Па —1 -с —1 ; RT = 3,3 - 107 Па.
Аналогичные рассуждения, проведенные для уравнений (5) и (6), дают следующие зависимости:
-
-
- c 2 " cx = ТТ ,
X
+
-
c, - c = —.
Получим соотношение, связывающее значения давлений и концентраций в симпласте по разные стороны от переходных слоев, примыкающих слева и справа к пояскам Каспари при r = r c . Учитывая, что в этих слоях давление и концентрация веществ в симпласте испытывают значительные изменения, в уравнении (4) можно пренебречь величиной скорости по сравнения со значениями производных давления и концентрации. Тогда после интегрирования уравнения (4) по переходной области получим
Р* - p2 =gRT(с +- с2).(11)
Сложение уравнений (1) и (2) приводит к условию постоянства полного радиального потока жидкости. Отсюда, с учетом граничных условий (7), следует, что
P1u1+ + р2u2+ = P1 u- + P2u2 = Р14 (Г0 )Г0 = P2v2 (rc )rc •
Сложим уравнения (5) и (6). Интегрирование полученного уравнения на отрезке [ r 0 ; rc ] с учетом граничных условий (7) и уравнения (12) дает
( cx - (1 -S) c 2( rc ) ) (P1 u- +P2 u 2 ) = P2D2 rc dc 2( rc ) • dr
Для получения полной системы алгебраических уравнений необходимо добавить два уравнения, связывающие c ( r ) и c 2 ( rc ) с другими неизвестными.
2 c dr
Рассмотрим асимптотику решения уравнения (6) в окрестности поясков Каспари. Учитывая сильное изменение концентрации в симпласте в этой области, можно пренебречь конвективным потоком растворенных веществ по сравнению с диффузионным. Чтобы проанализировать поведение решения в окрестности пограничных слоев слева и справа от r = rc, выполним преобразование растяжения соответствующих областей. Введем в каждой из них мелкомасштабную внутреннюю „- ± r - r „ + 1 Р2D _ переменную с = —, где а =— 2 ±2 - малые параметры. Знаки + и - указывают
£ ri \ X на то, что слева и справа от поясков Каспари используются различные новые переменные, а пограничные слои имеют разную толщину. Переходя к новой переменной, получим в пограничных слоях уравнение вида (знаки + и – для простоты опущены)
9 (d2 с, £ de,)
r 2 —2- +-- - - e 2 + e1 + —= 0.
( dC2 re + ас dC JX
В первом приближении по малому параметру распределение концентрации в окрестности точки r = re слева и справа имеет соответственно следующий вид:
c 2
k --Г
= e +---+ A • e r + B • e r 1
" X- c2
= e 0
k +
+ — + A ' • e r 1
X+
+ B + • e r 1
Выполним сращивание решений в пограничных слоях с внешним решением.
Будем использовать следующие условия сращивания [3]: lim e 2 = e 2 и lim e 2 = e + .
C ^ ^ c'^i^
k
+
Из этих условий получим, что A + = B = 0, e + — = e , eQ + — = e.
Л X- 2 ° X+ ■
■ |. Для определения
оставшихся постоянных интегрирования A и B + будем использовать условия непрерывности концентрации e 2 и диффузионного потока при r = re :
e +---+ A = e n +---+ A ,
" X- 0 X+
A -
X-p 2 D 2
- B
X+
V P2 D 2
Отсюда следует
+ k -
— e +
X+ X-
c 0
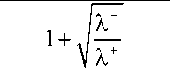
B + =
-
+ k -
— e +
X+ X-
c 0
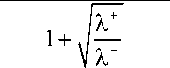
Теперь можно получить
k c 2( rc ) = cx +^- +
k + k - c — c„ +
0 x X+ X-
1 +
X
dc
2
(
r
c
)
=
V p
2
D
2
dr , X.
+
vx+
k
+
' 0
c
x
+ X
+
X Уравнения (8)–(14) образуют полную систему уравнений для нахождения dc2 (rc). dr
неизвестных
u
,
u
±
,
p
2
,
p
2
,
p
2*
,
p
*
,
p
**
,
c
±
,
c
x
,
c
2(
rc
) и
Расчеты и результаты В данном разделе в результате решения полученной системы уравнений будут найдены приближенные формулы, описывающие зависимость скорости течения от разности гидростатических давлений между окружающей средой и сосудами ксилемы, а также концентрации веществ в сосудах ксилемы от скорости потока на срезе корня. Складывая четвертое уравнение (8) с третьим уравнением (9) и вычитая из этой uu . суммы второе уравнение (8) и четвертое уравнение (9), получим равенство — = —
P
2
P
1
Выполняя аналогичные действия с третьим уравнением (8), первым уравнением (9), первым уравнением (8) и вторым уравнением (9), получим равенство — = —.
P
2
P
1
Учитывая полученные равенства и уравнение (12), находим, что
u
1
=
u
1
+
и
u
2
=
и
+
. В дальнейшем при этих величинах будем опускать верхние индексы.
Введем обозначение
u
=
— u
1
+ —
u
2, где
р = р
1
+ р
2. Тогда имеем выражения
Р Р
PiP u1 =------1------u р1Р1 + P2P2 P2P и u 2 =------2------u .
P
1
P
1
+ P
2
P
2
Складывая третье уравнение (8), четвертое уравнение (8), первое уравнение (9) четвертое уравнение (9), получаем и уравнение (11), а затем вычитая из этой суммы
p
0
-
px
=
- ln
r^ u
2
++
ln
r^ u
2
+
(
g-
1)
RT
(
c
+
P ' 2 V r
-
c
2
)
+
RT
(
c
0
-
cx
).
С учетом последних результатов это равенство можно переписать следующим образом:
ln
(rdrn
) P
-
p
x
=
R 0 R
u
+
(
g -
1)
RT
(
c
+
-
c
2
)
+
RT
(
c
0
-
c
x
) •
P
1
P
1
+P
2
P
2
Подставляя (14) в уравнение (13), найдем концентрацию низкомолекулярного компонента в сосудах ксилемы c x
л ч
Л
+
, k U
(1
- G
)
c
0 ' . . 1 .
К к
+
r
c
1
+S
7Р
2
К-
D
2
P
Величину
c
2
—
c
2
определим из уравнений (10):
c
+
-
c
2
k
+
k
-
—
c
0 —
c
+— ---
.
0
x
Г К
-
Алгебраические соотношения (15)–(17) дают интересующие нас зависимости концентрации в ксилеме
cx
и разности давлений между окружающей средой и ксилемой
A
p
—
p
0
—
p
x
от скорости
и
и, следовательно, от скорости вытекания жидкости через срез корня
J
—
2
uL / r
12
, где
L
- длина корня.
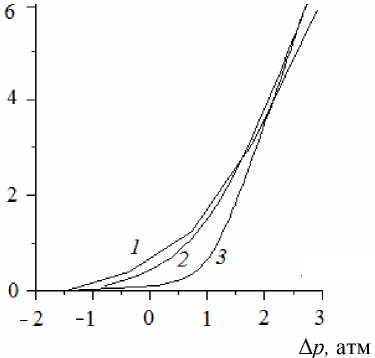
Численное решение и приближенные решения, полученные на основе двух компартментальных моделей (представленной соотношениями (15)–(17) и модели, сформулированной в работе [1]), сравнивались при одних и тех же значениях параметров. Результаты сравнения приведены на рис. 2 и 3. Видно, что полученные в настоящей работе соотношения с большей точностью совпадают с численным решением. В частности, наклон асимптоты, к которой приближается график зависимости потока от разности гидростатических давлений на рис. 2, полученный с помощью компартментальной модели [1], заметно отличается от наклона асимптоты функции, полученной из точного решения, тогда как в модели, представленной в настоящей работе, такого отклонения не наблюдается. Указанное расхождение может привести к значительным ошибкам в определении гидравлической проводимости корней. Источник ошибки – в неучете присутствия пограничных слоев. Сравнение с экспериментом было выполнено для численного решения ранее [10] и здесь не проводится.
v
-
10
8
, м/с
Рис. 2. Зависимость скорости потока на срезе корня от разности гидростатических давлений между окружающей средой и ксилемой:
1
– расчет на основе континуальной модели;
2
– расчет на основе предлагаемой модели;
3
– расчет на основе компартментальной модели [1]
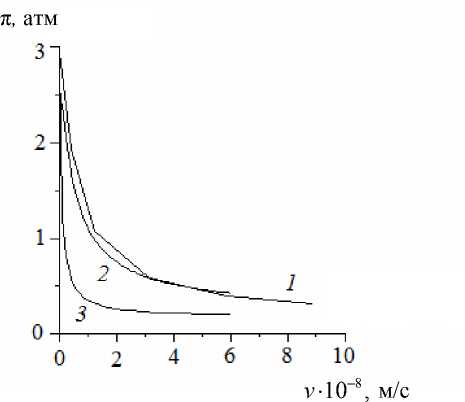
Рис. 3. Зависимость осмотического давления в ксилеме от скорости потока на срезе корня:
1
– расчет на основе континуальной модели;
2
– расчет на основе предлагаемой модели;
3
– расчет на основе компартментальной модели [1]
Предлагаемый метод получения конечных соотношений, структурно сходных с традиционными компартментальными моделями, имеет по сравнению с последними существенное преимущество: он позволяет учитывать особенности анатомического строения корня и неоднородность распределения величин по сечению. Это дает возможность получать простые приближенные зависимости, совпадающие с достаточной точностью с численным решением. Использование таких зависимостей оказывается значительно проще использования распределенных моделей или применения асимптотических методов. В рамках предлагаемого подхода модель может быть в случае необходимости модифицирована с учетом дополнительных возможных механизмов. Благодарности Работа поддержана РФФИ (проект № 11-01-00774).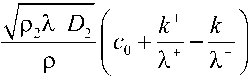
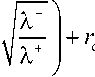
Список литературы Компартментальное моделирование транспортных процессов в корне растения, учитывающее присутствие пограничных слоев
- Логвенков С.А., Штейн А.А. Компартментальная модель поглощения воды корнями растений с учетом процессов на клеточном уровне//Российский журнал биомеханики. -2008. -Т. 12, № 4. -C. 18-32.
- Логвенков С.А., Штейн А.А. Влияние проницаемости поясков Каспари для воды и растворенных веществ на величину корневого давления. Математическое моделирование//Российский журнал биомеханики. -(Статья в настоящем выпуске).
- Найфэ А. Введение в методы возмущений. -М.: Мир, 1984. -535 с.
- Юдина Е.Н. Асимптотическое исследование транспортных процессов в корне растения//Российский журнал биомеханики. -2012. -Т. 16, № 2. -C. 59-67.
- Dalton F.N., Raats P.A.C., Gardner W.R. Simultaneous uptake of water and solutes by plant roots//Agronomy Journal. -1975. -Vol. 67. -P. 334-339.
- Fiscus E.L. Determination of hydraulic and osmotic properties of soybean root system//Plant Physiology. -1977. -Vol. 59. -P. 1013-1020.
- Ginsburg H. Model for iso-osmotic water flow in plant roots//Journal of Theoretical Biology. -1971. -Vol. 32. -P. 147-158.
- Miller D.M. Studies of root function in Zea mays. IV. Effects of applied pressure on the hydraulic conductivity and volume flow through excised root//Plant Physiology. -1985. -Vol. 77. -P. 168-174.
- Murphy R. Some compartmental models of the root: Steady-state behavior//Journal of Theoretical Biology. -2000. -Vol. 207. -P. 557-576.
- Stein A.A., Logvenkov S.A., Chalyuk A.T. Mathematical modelling of the plant root as a water-pumping cellular system//Mathematical modelling and computing in biology and medicine/ed. V. Capasso. -Bologna: Soc. Ed. Esculapio, 2003. -P. 206-212.


