Компенсация нелинейных искажений в многокаскадных усилителях

Одним из основных требований при проектировании радиоэлектронной аппаратуры для современных приложений является обеспечение низкого уровня нелинейных искажений (НИ) передаваемых и принимаемых сигналов. В работах [1–8] были предложены идеи компенсации интермодуляционных искажений в каскадах радиоприемных устройств, основанные на использовании дополнительного комбинационного взаимодействия спектральных составляющих второго порядка с основными частотами для нейтрализации прямого нелинейного взаимодействия основных частот. При этом используются типовые режимы и типовые схемы усилителей на полевых или биполярных транзисторах. Существенным условием для задействования этого механизма является широкополосное согласование двух последних каскадов и отсутствие существенных фазовых искажений сигналов в усилительных каскадах. Если последнее условие не выполняется, необходимы дополнительные корректирующие цепи, что, разумеется, усложнит схему. Предлагаемый компенсационный метод борьбы с НИ налагает определенные ограничения на коэффициент усиления предпоследнего каскада для выравнивания амплитуд спектральных компонент различного происхождения.

При линеаризации инерционных устройств на первый план выдвигаются ряды Вольтерры [9– 11], базирующиеся на разделении продуктов по уровням нелинейности. Именно ряды Вольтерры позволяют глубоко проникнуть в сущность физических явлений, проследить за вкладом в НИ источников различного происхождения, увидеть доминирующие источники и механизмы компенсации НИ. Если теория строится в предположении безынерционности нелинейных элементов и гармонических сигналов на входе, то наиболее предпочтительными являются степенные ряды. Предложенные компенсационные методы борьбы с интермодуляционными искажениями во входных усилителях ВЧ диапазона оказывают эффективными как для гармонических, так и широкополосных сигналов [8].

1. Последовательно-параллельная структура для компенсации НИ

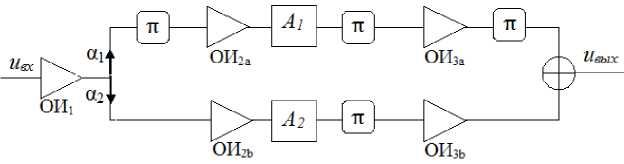
Рассмотрим многокаскадную структуру, содержащую последовательно и параллельно включенные усилители (рис. 1, а ). В работах [1–4] предложен способ устранения НИ четных порядков путем балансного включения двух последовательных структур, в каждой из которых скомпенсированы НИ третьего порядка. В n -каскадной структуре ( n - 3 ) данный

а )

б )

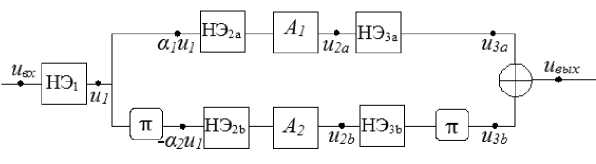
Рис. 1. Блок-схема ( а ) и модель ( б ) устройства для компенсации НИ

подход не приведет к полной компенсации НИ второго и третьего порядка, если включить балансным способом только оконечные усилители. Однако если обеспечить поступление сигнала в каждое из плеч в определенных, в общем случае неравных пропорциях, то удается полностью подавить НИ второго и третьего порядка. Структура похожа на балансное включение, но плечи не идентичны. Деление сигнала после первого каскада происходит в пропорциях a ^ , а 2 ( а 1 + а 2 = 1 ) без потерь полезного сигнала. При поиске эффективного решения ранее [3; 8] наиболее очевидным представлялся путь, когда каждое из плеч настраивается на минимум НИ третьего порядка в данном плече с последующим балансированием составляющих второго порядка из верхнего и нижнего плеч. Надлежащим подбором параметров аттенюаторов и/или коэффициентов усиления каскадов ОИ_2a и ОИ_2b можно одновременно устранить НИ второго и третьего порядка на выходе предлагаемой структуры. В данной работе рассматриваются другие подходы к решению задачи с получением противофазных компонент одновременно и второго и третьего порядка.

Поскольку усилители ОИ обладают инвертирующими свойствами, то последовательно-параллельную структуру на рис. 1, а можно заменить моделью (рис. 1, б ), более наглядно отображающей смысл спектральных преобразований.

2. Моделирование

С целью упрощения математических выкладок предполагалось, что все нелинейные элементы (НЭ) имеют характеристики в виде знакочередуемых полиномов

f ( и ) = a 1 и + a 2 и ² — a 3 и ^{3 a} 1 , a 2 , a 3 , — >  0.

—

a^u + a^u + — , ^{4        5           ,}      (1)

На вход многокаскадного усилителя воздействует двухтональный сигнал ивх = U01 cos «1t + + U02 cos «2t. После преобразования Ui = f (ивх ) в НЭ1 все спектральные составляющие, в т. ч. продукты интермодуляции второго и третьего порядка a2U01U02 cos («1 ± «2 ) t,

• ^—    4 a 3 ^U 01 ^U 02 ^cos ( ² « 1 ± « 2 ) t ,

• ^—    4 a 3 ^U 01 U 02 ^cos ( 2 « 2 ± « 1 ) t распределяются в пропорции a 1 : a 2 ( a 1 + a 2 = 1 ) между верхним и нижним каналами. В верхнем плече после прохождения НЭ_2a и аттенюатора A ₁ имеем

^u 2 a = f ( ^a 1 ^u 1 ) A 1 =

( ^b 1 ^ивх ^{+ b} 2 ^ивх

где

—

^b3^ивх ^— "• ) A 1 ,

b 1 = a a ,    b 2 = a 1 a 1 a 2 (a^ 1 + 1 ) ,

b 3 = ^a 1 a 1 a 3 ¹

I

—

a

2 a 1 -2- + a 2 a 2 ,

a ₃

при этом интермодуляционные продукты второго и третьего порядка b2A1U01U02 cos («1 ± «2 ) t,

—

—

4 ^b 3 A 1 U 01 U 02 cos ^{( 2} « 1 ± « 2 ) t ,

4 ^b 3 A 1 U 01 U 02 cos ( 2 ® 2 ± « 1 ) t .

Аналогично в нижнем плече после инверсии напряжения, НЭ_2b и аттенюатора A ₂

а )

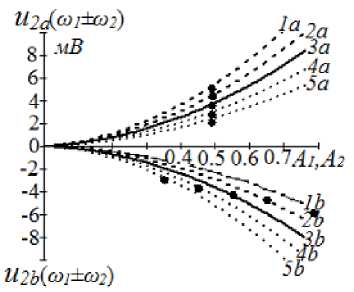
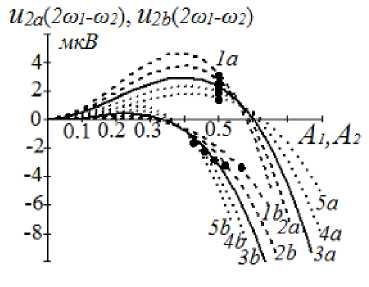
Рис. 2. Продукты интермодуляции второго порядка ( а ) и третьего порядка ( б ) в верхнем и нижнем каналах в зависимости от затухания в аттенюаторах. Кривые: 1 — а = 0.6; 2 — а = 0.55; 3 — а = 0.5; 4 — а = 0.45; 5 — а = 0.4

б )

^u2a = f ( ^-a 2 u i ) A 2 =

= (—ci ивх + c2 u2х + c3 u3х — —) A2, где

c i = « 2 a 2 ,    1

c 2 = « 2 a 1 a 2 ( ^а 2 a i ^— 1 ) ,

На частотах to i ± to 2 ^ивых ^(to i ± ^to 2 ) =

= ( a i ^b 2 A i ⁺ a 2 ^b l A l ^— a i ^c 2 A 2 ^— a 2 c ² A 2 ) ^{x          (8)}

X U 0i U 02 cos ( to i ± to 2 ) t .

^c 3 = ^a 2 a i a 3 ^{1 + 2 a} 2 “2 ^{+ a} 2 a ² ,

к

a ₃

при этом интермодуляционные продукты второго и третьего порядка

• ^c 2 A 2 U 0i U 02 ^{cos (to} i ± ^to 2 ) t ,

• 4 ^c 3 A 2 U 0i U 02 ^{cos ( 2 to} i ± ^to 2 ) t ,

• 4 ^c 3 A 2 U 0i U 02 ^{cos ( 2 to} 2 ± ^to i ) t ■

В конце верхнего плеча после преобразования u 3 a = f ( U a ) на НЭ з _а интермодуляционный продукт третьего порядка (в дальнейшем для определенности рассматривается частота 2 to i — to 2 ) равен

• u3a (2toi - to2 ) =

• = — 4 ( a ^b A i — ² a 2 ^b i ^b 2 A i ⁺ a 3 ^b 3 A ³ ) ^X

x U 0i U 02 cos ( 2 to i — to 2 ) t .

В нижнем плече после преобразования на НЭ_3b и инверсии фазы u 3 ь =— f ( U 2 ь ) продукт интермодуляции на частоте 2 to i — to 2

• u3b (2toi — to2 ) =

• = ^— 4 ( a i ^c 3 A 2 ^{— 2} a 2 ^c i ^c 2 A 2 ⁺ a 3 ^c l A 2 ) ^x

• x U 0i U 02 cos ( 2 to i ± to 2 ) t .

Окончательно, в результате суммирования сигналов отдельных каналов на выходе имеем на основных частотах to i , to 2

На частоте 2 to i — to 2 (на частоте 2 to 2 — to i аналогично)

ивых (2toi — to2 ) =

= ^— t( a i ^b 3 A i ^{— 2} a 2 ^b i ^b 2 A l ⁺ a 3 ^b l A l ⁺

⁴                                                  (9)

+ aiC3A2 — 2a2CiC2A2 + a3c3A3) x x U0iU02 cos (2toi — to2 ) t.

Для компенсации составляющих второго порядка коэффициенты передачи аттенюаторов в верхнем и нижнем плечах должны быть связаны соотношением aib2 Ai + a 2 b2 A2 = ai c2 A2 + a 2 cl A2 .             (l0)

Условие компенсации оставляющих третьего порядка требует одинакового вклада в НИ первичного взаимодействия основных частот и повторного взаимодействия основных частот с

продуктами второго порядка a i ^b 3 A i ⁺ a i ^c 3 A 2 ⁺ a 3 ^b 3 A 3 ^{+ +} a 3 ^c l A 2 = ² a 2 ^b i ^b 2 A l ^{+ 2} a 2 ^c i ^c 2 A 2 .

u вых ( to i ) = a i ( b i A i + c i A 2 ) U 0 i cos to i t .

3. Результаты расчетов

На рис. 2, а показаны составляющие второго порядка в верхнем и нижнем плечах для пяти вариантов a ( a 2 = l — a ) . Вследствие балансного включения усилителей составляющие второго порядка в каналах находятся в противофазе. Однако в каждом из каналов фаза составляющих второго порядка не меняется. С помощью аттенюаторов можно выровнять их амплитуды

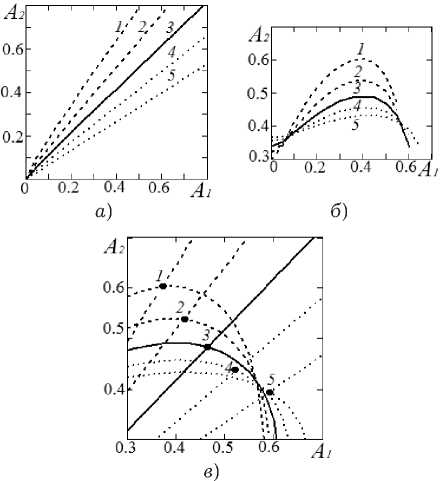
Рис. 3. Соотношения между коэффициентами передачи аттенюаторов при компенсации интермодуляции второго порядка ( а ), третьего порядка ( б ); одновременная компенсация продуктов интермодуляции в точках пересечения кривых ( в ). Нумерация кривых такая же, как на рис. 2

при любых пропорциях без ограничения. Например, при А 1 = 0, 5 и набора значений « 1 (0.4, 0.45, 0.5, 0.55, 0.6) A ₂ должно быть соответственно равно 0.33, 0.42, 0.52, 0.64, 0.79.

На рис. 2, б изображены составляющие третьего порядка в верхнем и нижнем плечах для тех же вариантов. Типичная фаза составляющих третьего порядка имеет отрицательный знак, но на любой приведенной кривой знак изменяется, т. е. составляющие третьего порядка в верхнем и нижнем каналах могут находиться в противофазе. Эффект обусловлен наличием достаточно интенсивного взаимодействия основных частот с составляющими второго порядка. При увеличении масштаба можно увидеть, что любая кривая изменяет знак дважды. Однако в области низких значений коэффициентов A ₁, A ₂ факт смены знака малоинтересен. С помощью аттенюаторов в определенном диапазоне изменения A ₁, A ₂ можно выходить на участки про-тивофазности составляющих третьего порядка в верхнем и нижнем плечах и выравнивать их амплитуды. Например, при A 1 = 0,5 и рассмотренных вариантов « 1 (0.4, 0.45, 0.5, 0.55, 0.6) A 2 должно быть соответственно равно 0.42, 0.44, 0.47, 0.51, 0.55. Все зависимости приведены для 2

a 2 / a y a 3 = 2.5, т. е. достаточно высокого уровня 2

квадратичной нелинейности. Если a 2 / a y a 3 <  1, то будет происходить только частичная компенсации продуктов третьего порядка, и необходимы дополнительные меры.

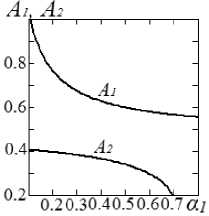
Рис. 4. Зависимости коэффициентов передачи аттенюаторов от параметра « 1

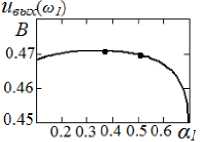
Рис. 5. Выходной сигнал линеаризованного устройства на основных частотах

На рис. 3, а показаны соотношения между коэффициентами A ₁, A ₂, которые обеспечивают подавление составляющих второго порядка при различных соотношениях a y , « 2 . Здесь нейтрализованы только НИ второго порядка, а НИ третьего порядка остаются. Напротив, соотношения между коэффициентами A ₁, A ₂ на рис. 3, б обеспечивают полное подавление составляющих третьего порядка с сохранением продуктов второго порядка. На рис. 3, в зависимости совмещены, при этом отчетливо видно, что есть точки пересечения кривых. Иными словами, при изменении a ₁, a ₂ в определенных пределах, включая точку a y = « 2 = 0.5, можно получить одновременную компенсацию НИ и второго, и третьего порядка. На рис. 4 приведены зависимости коэффициентов передачи A ₁, A ₂ от a ₁, при которых на выходе отсутствуют одновременно искажения второго и третьего порядка. Положительным моментом является то, что сигнал может распараллеливаться в равных пропорциях « у = « 2 = 0.5. Это реализуется практически проще по сравнению с делением сигнала в неравных пропорциях. В случае компенсации НИ в каждом плече, компенсация наблюдается только при единственном наборе значений: « 1 = 0.37 и A 1 = 0.64, A 2 = 0.37.

На рис. 5 приведена зависимость выходного сигнала на одной из основных частот от «у при условии, что нейтрализованы продукты второго и третьего порядка одновременно. При «1 = «2 = 0.5 (равное деление сигнала по каналам) и «1 = 0.37, «2 = 0.63 (компенсация НИ третьего порядка в каждом плече) выходные сиг- налы на основных частотах практически не отличаются.

Заключение

Таким образом, предложенные компенсационные методы борьбы с интермодуляционными искажениями во входных усилителях ВЧ диапазона допускают более оптимальную реализацию по сравнению с ранее полученными результатами. Возможный проигрыш в суммарном коэффициенте усиления каскадов из-за включения аттенюаторов можно восстановить введением дополнительного усилительного звена со стороны входа, и серьезной деградации других параметров при линеаризации устройства не должно происходить. В целом идея представляется полезной с практической точки зрения и достаточно легко реализуемой (во всяком случае, в низкочастотных усилителях). Хотя теория с компенсационным механизмом устранения НИ развивается в предположении разделения продуктов по уровням нелинейности, она достаточно хорошо подтверждена результатами экспериментов на макетах усилителей.

Работа выполнена при поддержке Минобрна^ уки России в рамках государственного задания ВУЗам в сфере научной деятельности на 2014– 2016 годы (Проект № 978).