Компьютерная модель устройства фильтрации сигнала для мониторинговой земной станции

На сегодняшний день большое значение в жизни общества оказывают технические средства связи, коммуникации и навигации. В зависимости от назначения и условий использования данные системы и их техническая реализация могут быть различны. Для того чтобы определить координаты объекта либо же обеспечить передачу информации из отдаленных территорий земного шара, где установка наземных систем связи не рентабельна или даже невозможна, применяются системы спутниковой связи. Они имеют преимущество перед другими системами связи, так как имеют большой охват территории. Земная спутниковая станция может быть как спутниковым пиратом (нелегитимным пользователем) так и легитимным пользователем. Перед разработчиками стоит задача определить координаты незаконно занимающего частотный ресурс нелегитимного пользователя [1].

Рассмотрим реализацию фильтра, входящего в состав устройства определения координат (УОК) [2]. Для этого сформируем структуру устройства фильтрации, проведем обзор существующих аналогов устройства фильтрации и разработаем компьютерную модель устройства фильтрации с возможностью определения набега фазы.

1.    Формирование структуры устройства фильтрации

На рис. 1 приведена общая структурная схема мониторинговой земной станции [2], в состав которой входит УОК.

Рис. 1. Общая структурная схема мониторинговой земной станции: УВЧ – усилитель высокой частоты, ПЧ – преобразователь частоты

УОК должна содержать [2]: фильтр (Ф), который позволит выделить гармоническую составляющую сигнала (нелегитимного пользователя) с неизвестной структурой, принятую с искус- ственного спутника земли (ИСЗ); фазометр (Фаз.), который содержит, кроме измерителя разности фаз, аналого-цифровой преобразователь и память и который, в свою очередь, позволит произвести измерение разности фаз по алгоритму, изложенному в [3]; ЭВМ, в которой заложен алгоритм [1], с помощью которого будет произведено определение координат нелегитимного пользователя. Структурная схема УОК представлена на рис. 2.

Ф

Фаз.

ЭВМ

Рис. 2. Структурная схема УОК

В связи с тем, что используется фазовый метод определения координат, на выходе фильтра (устройства фильтрации) требуется знать набег фазы при прохождении через него сигнала.

Также для высокоточного определения разности фаз должно быть минимальное искажение сигнала и постоянное слежение за частотой [4]. Учитывая предъявляемые требования, структура устройства фильтрации должна состоять из двухуровневой фильтрации и системы фазовой автоподстройки частоты (ФАПЧ) (рис. 3).

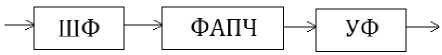
Рис. 3. Структурная схема фильтра (устройства фильтрации): ШФ – широкополосный фильтр, предназначен для предварительной фильтрации сигнала на входе ФАПЧ; ФАПЧ – предназначен для слежения за частотой; УФ – узкополосный фильтр, предназначен для увеличения отношения сигнал/шум на выходе устройства фильтрации

Проведем обзор существующих имитационных моделей устройств фильтрации.

2.    Аналоги устройства фильтрации

Существует патент «Способ восстановления несущей частоты фазоманипулированного сигнала и слежения за ней» [5]. Предложенный в патенте способ относится к области радиотехники и может быть использован при реализации систем

Том 7

связи и радионавигации с фазоманипулированны-ми сигналами. Достигаемый технический результат – восстановление сигнала несущей частоты из принятого фазоманипулированного сигнала, искаженного шумами, с уменьшением дисперсии фазовых шумов в шумовой полосе ФАПЧ. Способ восстановления несущей частоты фазоманипули-рованного сигнала и слежения за ней характеризуется тем, что синфазный опорный сигнал, являющийся сигналом восстановленной несущей, формируют посредством фазовой модуляции гармонического сигнала, создаваемого автономным генератором, в соответствии с сигналом, получаемым при интегрировании профильтрованного сигнала в фильтре кольца ФАПЧ.

Структурная схема восстановления несущей частоты фазоманипулированного сигнала и слежения за ней представлена на рис. 4.

Данный способ восстановления сигнала для использования в устройстве определения координат не подходит, так как в данном случае извлекается несущая из сигнала с заранее известным видом, а именно фазоманипулированного сигнала. Устройство фильтрации, входящее в состав УОК, в свою очередь должно выделять любую спектральную составляющую. Кроме того, на данную структурную схему восстановления несущей частоты фазоманипулированного сигнала нет ее компьютерной модели для анализа работы схемы.

Существует патент «Фильтр с переменной полосой пропускания для подавления узкополосного шума и модуль регулируемой задержки» [6]. Данное запатентованное изобретение относится к технике связи. Его цель заключается в повышении помехоустойчивости. Для достижения повышения помехоустойчивости в системе используют фильтры управляемой ширины полосы пропускания для фильтрации принимаемого сигнала. Управляющая схема генерирует сигнал управления, чтобы управлять шириной полосы пропускания фильтров. Если интенсивность принимаемого сигнала выше первого порогового значения, то для фильтров может использоваться более широкая полоса пропускания. Если принимаемый сигнал ниже второго порогового значения, то управляющая схема ге-

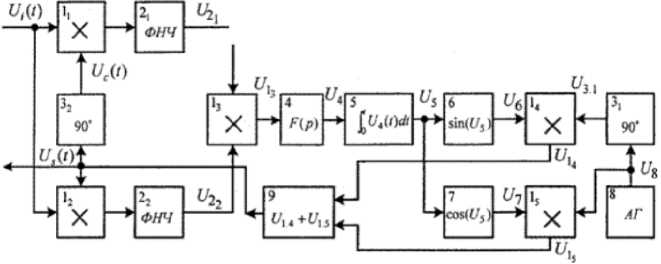
Рис. 4. Структурная схема восстановления несущей частоты фазоманипулированного сигнала и слежения за ней

нерирует сигнал управления для настройки фильтров на более узкую полосу пропускания. Ширина полосы пропускания фильтра также изменяется в зависимости от присутствия источника узкополосных радиопомех (преднамеренных радиопомех). Блок регулируемой задержки гарантирует постоянное групповое время задержки между всеми возможными конфигурациями фильтра.

Данное изобретение не подходит для использования в УОК, так как в данной модели фильтра устройства определения координат нет возможности слежения за частотой принимаемого сигнала для измерения фаз, которое требуется. Уход частоты сигнала не позволит снимать ее истинные значения, что приведет к невозможности применения данного фильтра для определения координат фазовым методом.

Существует научная статья «Цифровой фильтр для устройства определения координат источника радиосигнала в спутниковых системах телекоммуникаций» [2]. В данной статье проводится исследование зависимости мощности сигнала, который используется в измерениях разности фаз устройством определения координат, и шумовых составляющих сигнала от типа цифрового фильтр и его параметров при различных соотношениях сигнал/шум.

В качестве устройства фильтрации разработчики предлагают использовать полосно-пропуска-ющий цифровой фильтр. В ходе научной работы авторами была создана компьютерная модель для исследования цифрового фильтра, которая изображена на рис. 5, а также рассмотрены исследования для цифровых рекурсивных полосно-пропускаю-щих фильтров типа Баттерворта, Чебышева 1 рода, ⁷⁷ Чебышева 2 рода, Золотарева-Кауэра, которые задаются с помощью дискретной линейной системы.

В данной модели фильтра устройства определения координат нет возможности слежения за частотой принимаемого сигнала для высокоточного измерения фаз.

Разработаем компьютерную модель устройства фильтрации, используя программу MatLAB Simulink.

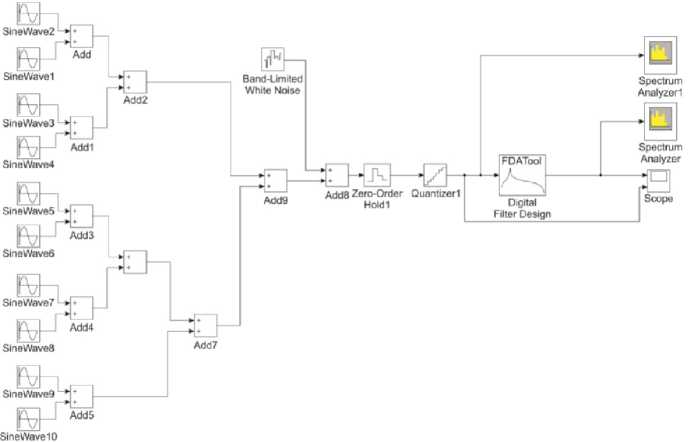
Рис. 5. Компьютерная модель для исследования цифрового фильтра

3.    Компьютерная модель устройства фильтрации

В качестве широкополосного и узкополосного фильтра устройства фильтрации применим блок аналогового фильтра Analog Filter Design, который представлен на рис. 6.

Рис. 6. Блок аналогового фильтра Analog Filter Design

ШФ и УФ являются полосно-пропускаю-щим фильтром с настройками, приведенными на рис. 7 а (для ШФ) и на рис. 7 б (для УФ). В настройках блока можно установить: метод проектирования (Design method), тип фильтра (Filter type), порядок фильтра (Filter order), верхнюю (Lower passband edge frequency) и нижнюю частоты полосы пропускания (Upper passband edge frequency).

На рис. 8 рассмотрены амплитудно-частотные характеристики (АЧХ) и фазочастотные характеристики (ФЧХ) пяти возможных типов проектирования полосовых фильтров первого порядка с заданными верхней ( f _в ) и нижней ( f _н ) частотами среза: Баттерворда (Butterworth), Чебышева 1 (Chebyshev1) с пульсацией полосы пропускания

Том 7

2 дБ, Чебышева 2 (Chebyshev2) с затуханием в по- с пульсацией полосы пропускания 2 дБ и затухани-лосе задерживания 40 дБ, Эллиптический (Elliptic) ем в полосе задерживания 40 дБ, Бесселя (Bessel).

И Block Parameters: ШФ

Analog Filter Design (mask) (link)

Design one of several standard analog filters, implemented in statespace form.

X Q Block Parameters: УФ

Analog Filter Design (mask) (link)

Design one of several standard analog filters, implemented in statespace form.

Parameters

Design method: Butterworth

Filter type: Bandpass

Filter order:

Parameters

Design method: Butterworth

Filter type: Bandpass

Filter order:

Ы	1
Lower passband edge frequency (rad/s):	Lower passband edge frequency (rad/s):
59061941.89                                                    i	59690260.42
Upper passband edge frequency (rad/s):	Upper passband edge frequency (rad/s):
66601764.26                                                    I	65973445.73

б

а

Рис. 7. Панель настройки: а – ШФ, б – УФ

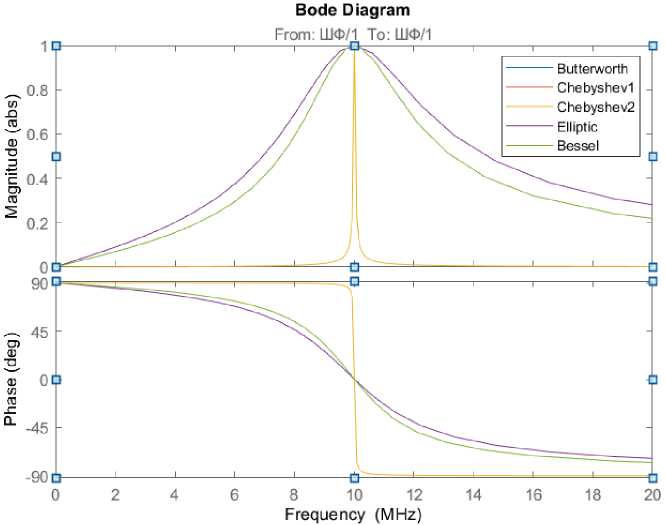
Рис. 8. АЧХ и ФЧХ фильтров Баттерворда (Butterworth), Чебышева 1 (Chebyshev1), Чебышева 2 (Chebyshev2), Эллиптический (Elliptic), Бесселя (Bessel)

По рис. 8 видно, что при данных настройках фильтры Чебышева 1 и Эллиптический одинаковы между собой. Также при данных настройках одинакова пара фильтров Баттерворда и Бесселя. Таким образом, зная возможности регулировки данных фильтров, анализируя АЧХ и ФЧХ и уже подавая в систему сигнал с шумом, можно исследовать фильтр под заданные требования с настройками как у широкополосного фильтра, так и у узкополосного фильтра для того, чтобы получить требуемое значение сигнала на выходе устройства фильтрации.

Возьмем фильтр для проверки влияния с типом реализации Баттерворда. Порядок ШФ принимаем равным 3.

Нижняя и верхняя частоты среза подбираются таким образом, чтобы на центральной частоте, например 10 МГц, ФЧХ равнялась нулю, то есть на этой частоте не было фазового сдвига. Аналитическим методом определяем верхнюю ( f _в ) и нижнюю ( f _н ) частоты среза ШФ. Анализ показал следующие значения частот: f _н = 8,5 МГц; f в = 11,760323 МГц. Диаграмма АЧХ и ФЧХ ШФ приведена на рис. 9.

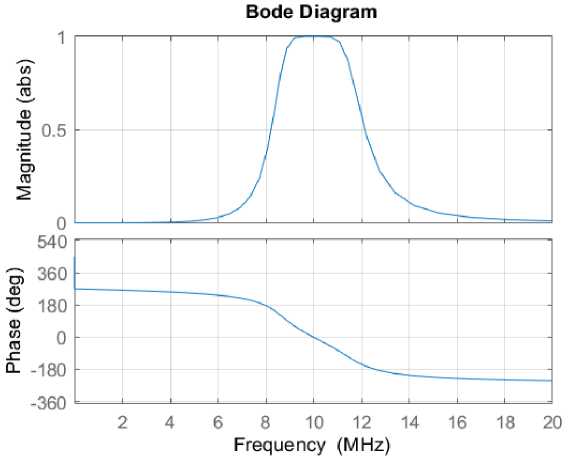
Рис. 9. Диаграмма АЧХ и ФЧХ ШФ

Для того чтобы определить изменения фазы сигнала, вносимые данным фильтром в систему, следует зафиксировать значения ФЧХ ШФ. Зная частоту сигнала на выходе устройства и отклонение фазы фильтром на этой частоте, можно математически рассчитать фазу сигнала на входе фильтра.

Фиксированные значения ФЧХ, где ∆φ – отклонения фазы (град.) при значении частот f в по- лосе 9–11 МГц с дискретностью взятия отсчетов по частоте 100 кГц, приведены в табл. 1.

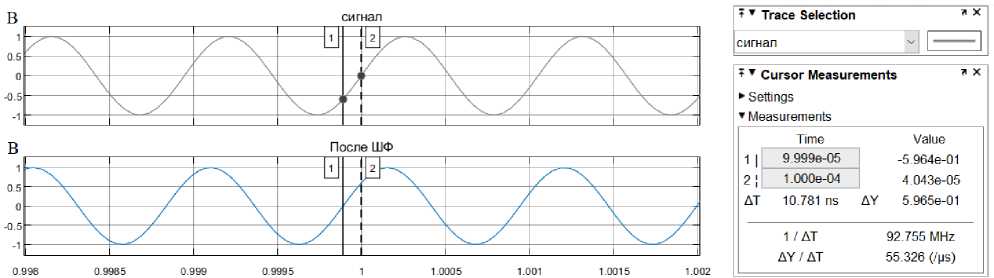
По частоте сигнала с помощью данных значений отклонения фаз на выходе фильтра можно восстановить входную фазу сигнала. Произведем проверку восстановления сигнала, подавая на вход данного фильтра сигнал с частотой 9,5 МГц. Результат приведен на рис. 10.

Таблица 1

к ю"’ сек.

Рис. 10. Временной график входного и выходного сигнала ШФ

ФЧХ ШФ от частоты входного сигнала фильтра

f	∆ φ	f	∆ φ	f	∆ φ
9	81,5	9,7	21,4	10,4	–28,2
9,1	71,7	9,8	14,2	10,5	–35,3
9,2	61,8	9,9	7,12	10,6	–42,3
9,3	53,5	10	0	10,7	–49,4
9,4	45,4	10,1	–7,17	10,8	–57,1
9,5	37	10,2	–14,1	10,9	–64,8
9,6	29	10,3	–21,2	11	–72,6

Таблица 2

ФЧХ УФ от частоты входного сигнала фильтра

f	∆ φ	f	∆ φ	f	∆ φ	f	∆ φ	f	∆ φ
9	493	9,41	249	9,82	49,7	10,23	–137	10,64	–328
9,01	486	9,42	244	9,83	45	10,24	–142	10,65	–333
9,02	478	9,43	239	9,84	40,4	10,25	–146	10,66	–338
9,03	471	9,44	234	9,85	35,8	10,26	–151	10,67	–343

Параметр ∆T = 10,781∙10^-9 с на рис. 11 показывает разницу во времени между маркерами 1 и 2. Маркеры установлены в нулевых фазах входного и выходного сигнала фильтра соответственно. Таким образом, зная смещение сигнала во времени, можно получить разность фаз сигнала на входе и выходе ШФ:

360 Δϕ fсигн

1 _{Δ T} ^,                  (1)

сигн где fсигн – частота входного сигнала; ∆φf   – раз-

⁸⁰ ница фаз входного и выходного сигнала. ^сигн

Аф.  = 360 -10,781 -10 - 9 - 9500000 = 36,87°.

f сигн

Расчетное математически значение из временных графиков рис. 11 и значения ФЧХ из табл. 1 практически равны, что доказывает возможность определения набега фазы сигнала после прохождения его через ШФ.

Для УФ, анализируя графики типов проектирования фильтров рис. 9, выбор останавливается на типе реализации Баттерворда. Данный фильтр имеет максимально гладкую АЧХ на частотах полосы пропускания и снижающуюся почти до нуля на частотах подавления [7]. УФ должен не искажать амплитуду сигнала в полосе пропуска-

Том 7

ния и при этом иметь полосу пропускания меньше, чем у ШФ. Также, УФ должен иметь более высокое отношение сигнал/шум, чем ШФ, обладая высоким уровнем затухания в полосе задерживания. Для того чтобы АЧХ имела резкий переход между полосами среза и задерживания, необходимо выбрать высокий порядок фильтра.

Корректируя АЧХ под требуемую форму, уменьшая уровень затухания в полосе задерживания, получаем требование для порядка ШФ, равное 15. Такой высокий порядок фильтра приводит к тому, что фильтр будет иметь высокие искажения фазы, следовательно, дискретность взятия отсчетов ФЧХ по частоте нужно взять заметно больше, чем у ШФ.

Нижняя и верхняя частоты среза подбираются таким образом, чтобы АЧХ имела максимально ровную полосу пропускания в диапазоне частот от 9 до 11 МГц. Аналитическим методом определяем значения верхней ( f _в ) и нижней ( f _н ) частотам среза УФ. Анализ показал следующие значения: f _н = 8,8 МГц, f _в = 11,2 МГц. Диаграмма АЧХ и ФЧХ УФ приведена на рис. 11.

Фиксированные значения ФЧХ, где ∆ φ – отклонения фазы (град.) при значении частот f в полосе 9–11 МГц с дискретностью взятия отсчетов по частоте 10 кГц, приведены в табл. 2.

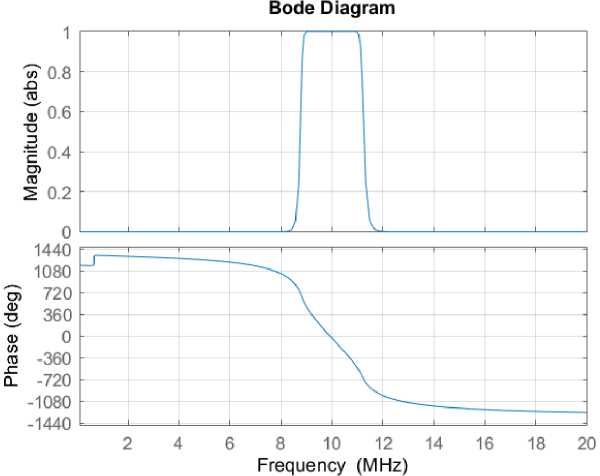
Рис. 11. Диаграмма АЧХ и ФЧХ УФ

Окончание таблицы 2

f	∆ φ	f	∆ φ	f	∆ φ	f	∆ φ	f	∆ φ
9,04	468	9,45	229	9,86	31,2	10,27	–155	10,68	–348
9,05	458	9,46	224	9,87	26,6	10,28	–160	10,69	–353
9,06	451	9,47	219	9,88	21,9	10,29	–164	10,7	–358
9,07	445	9,48	214	9,89	17,4	10,3	–169	10,71	–363
9,08	439	9,49	208	9,9	12,8	10,31	–173	10,72	–368
9,09	432	9,5	203	9,91	8,15	10,32	–178	10,73	–373
9,1	429	9,51	198	9,92	3,56	10,33	–183	10,74	–378
9,11	420	9,52	193	9,93	–1,03	10,34	–187	10,75	–383
9,12	413	9,53	188	9,94	–5,57	10,35	–192	10,76	–388
9,13	407	9,54	183	9,95	–10,2	10,36	–196	10,77	–393
9,14	400	9,55	178	9,96	–14,7	10,37	–201	10,78	–398
9,15	394	9,56	173	9,97	–19,2	10,38	–206	10,79	–403
9,16	388	9,57	168	9,98	–23,8	10,39	–210	10,8	–409
9,17	382	9,58	164	9,99	–28,3	10,4	–215	10,81	–414
9,18	376	9,59	159	10	–32,9	10,41	–219	10,82	–419
9,19	370	9,6	154	10,01	–37,4	10,42	–224	10,83	–425
9,2	364	9,61	149	10,02	–42	10,43	–229	10,84	–430
9,21	358	9,62	144	10,03	–46,5	10,44	–233	10,85	–436
9,22	353	9,63	139	10,04	–51	10,45	–238	10,86	–441
9,23	347	9,64	134	10,05	–55,6	10,46	–242	10,87	–447
9,24	342	9,65	130	10,06	–60,1	10,47	–247	10,88	–452
9,25	336	9,66	125	10,07	–64,7	10,48	–252	10,89	–457
9,26	330	9,67	120	10,08	–69,7	10,49	–256	10,9	–463
9,27	325	9,68	115	10,09	–73,7	10,5	–261	10,91	–469
9,28	319	9,69	111	10,1	–78,2	10,51	–266	10,92	–475
9,29	314	9,7	106	10,11	–82,7	10,52	–271	10,93	–481
9,3	308	9,71	101	10,12	–87,2	10,53	–275	10,94	–486
9,31	302	9,72	96,5	10,13	–91,8	10,54	–280	10,95	–492
9,32	297	9,73	91,7	10,14	–96,3	10,55	–285	10,96	–498
9,33	291	9,74	87	10,15	–101	10,56	–289	10,97	–504
9,34	286	9,75	82,3	10,16	–105	10,57	–294	10,98	–510
9,35	281	9,76	77,6	10,17	–110	10,58	–299	10,99	–516
9,36	275	9,77	72,9	10,18	–114	10,59	–304	11	–523
9,37	270	9,78	68,1	10,19	–119	10,6	–309
9,38	265	9,79	63,5	10,2	–123	10,61	–314
9,39	259	9,8	58,9	10,21	–128	10,62	–319
9,4	254	9,81	54,2	10,22	–132	10,63	–323

С помощью значений отклонения фаз сигнала УФ табл. 2 и значения частоты сигнала на выходе этого фильтра можно установить набег фазы.

Основными элементами системы ФАПЧ являются фазовый детектор (ФД), фильтр нижних частот (ФНЧ) и генератор, управляемый напряжением (ГУН). Существенной особенностью системы

ФАПЧ является то, что выходной величиной ГУН является частота, а входной величиной ФД – разность фаз управляющего сигнала и сигнала обратной связи, поступающего с выхода ГУН [8].

Фазовый детектор – устройство, осуществляющее сравнение двух входных частот, и формирующее выходной сигнал, длительность которого

Том 7

пропорциональна этой разности. При реализации цифрового ФД используется схема «исключающего или», а при реализации аналогового ФД используется схема аналогового умножителя сигналов [9]. При сборке в программе схемы фазового детектора необходимо выбрать блок аналогового умножения сигналов и блок усиления сигнала. Блок аналогового умножения сигналов Product приведен на рис. 12 а . Результат перемножения двух сигналов необходимо усилить. Для этого необходимо применение блока усиления сигнала Gain, который приведен на рис. 12 б .

б

а

Рис. 12. Составной блок ФД: а – аналогового умножения сигналов Product, б – усиления сигнала Gain

пряжения данный блок смещает частоту генерируемого сигнала в зависимости от величины управляющего напряжения. Если входной сигнал равен u ( t ), то выходной сигнал соответствует формуле:

t

y ( t ) = A _v cos(2n f co t + 2n k c J u ( t ) d т + ф),   (2)

где A_cg – амплитуда входного сигнала, f_co – частота покоя, t – время, k_c – входная чувствительность, φ – начальная фаза.

Блок ГУН Continuous-Time VCO имеет настройки: выходная амплитуда (Output amplitude), частота покоя (Qulescent frequency), входная чувствительность (Input sensitivity) и начальная фаза (Initial phase).

Сборная модель системы ФАПЧ приведена на рис. 13.

Таким образом, с помощью блоков Product и Gain сформирована схема фазового детектора, собранная в один блок, изображенный в модели ФАПЧ на рис. 13.

На выходе ФД применяется ФНЧ. Цель ФНЧ – подавить высокочастотную составляющую сигнала, сохранив сигнал нулевой частоты, который должен регулировать ГУН. Для выполнения функций ФНЧ в программе MatLAB Simulink подходит блок Analog Filter Design. Блок ФНЧ Analog Filter Design приведен в модели ФАПЧ на рис. 13. Данный блок такой же, как у ШФ и УФ, отличающийся только настройкой параметра типа фильтра. Он имеет настройки: метод проектирования (Design method), тип фильтра (Filter type), порядок фильтра (Filter order) и граничная частота полосы пропускания (Passband edge frequency (rad/s)).

В ФАПЧ ГУН является генератором, у которого частота на выходе зависит от напряжения на его управляющем входе [10]. Блоком ГУН в программе MatLAB Simulink является блок ContinuousTime VCO, изображенный в модели ФАПЧ на рис. 13. Данный блок предназначен для непрерывных сигналов. Под действием управляющего на-

Рис. 13. Модель системы ФАПЧ

Таким образом, цель сборки модели ФАПЧ успешно достигнута.

В результате моделирования системы ФАПЧ в диапазоне частот от 9 МГц до 11 МГц фаза сигнала на выходе смещается на 90 градусов относительно входного сигнала за счет ГУНа.

На рис. 14 представлена разработанная общая компьютерная модель устройства фильтрации в программе MatLAB Simulink.

Входной сигнал формируется из суммы двух блоков генерации: генератор сигнала (Signal Generator) и генератор нормального распределения случайных чисел (Random Number). Параметры сигнала и белого шума также регулируются.

Заключение

Таким образом, проведенный обзор аналогов предложенной структуры устройства фильтрации показал отсутствие компьютерной модели с возможностью слежения за частотой сигнала и оценки влияния параметров элементов устройства на фазу сигнала. В результате была разработана ком-

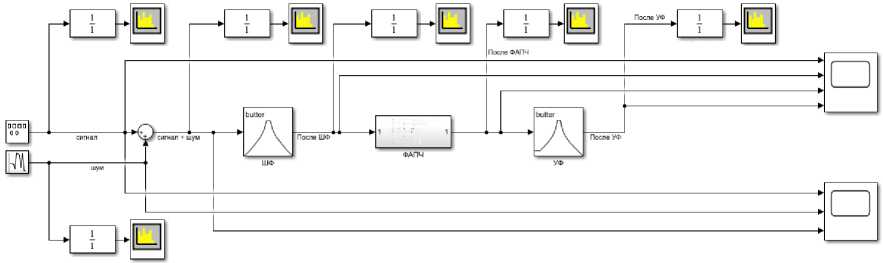
Рис. 14. Модель устройства фильтрации

пьютерная модель устройства фильтрации в программе MatLAB Simulink, в которую вошли: ШФ и УФ с возможностью изменения их параметров (частоты среза и задерживания, типа реализации фильтра, порядка фильтра), ФАПЧ с возможностью изменения ее параметров (коэффициента усиления в ФД, чувствительности ГУН, частоты покоя ГУН и ряда других параметров) и схемотехнического решения.

Разработанная компьютерная модель позволит провести исследования влияния блоков устройства фильтрации на фазу сигнала.

Исследование выполнено в рамках государственного задания ФГАОУ ВО «Сибирский федеральный университет» (номер FSRZ-2023-0008).