Компьютерное моделирование автоматического управления сельскохозяйственным малым беспилотным летательным аппаратом с переменной массой

ТЕХНОЛОГИИ, МАШИНЫ И ОБОРУДОВАНИЕ / TECHNOLOGIES, MACHINERY AND EQUIPMENT

EDN:

В условиях интенсификации сельскохозяйственного производства вопросы управления технологическими процессами без участия человека становятся все более востребованными. Наравне с наземными мобильными машинами [1] в сельскохозяйственном производстве активно используются летательные аппараты, при этом «возможности применения малых беспилотных летательных аппаратов в сельском хозяйстве оказались гораздо шире их изначального основного назначения» [2]. Одна из областей их применения связана с обработкой полей препаратами для уничтожения вредителей, а также с внесением удобрений. Полеты осуществляются на небольшой высоте, и, во избежание нарушения норм внесения активного вещества на единицу площади поля, необходимо обеспечить равномерность внесения препаратов за счет поддержания заданной высоты полета над поверхностью поля и скорости малых беспилотных летательных аппаратов (МБЛА). Такой режим полета можно обеспечить за счет соответствующего управления рулем высоты и тягой двигателя. При этом необходимо учесть, что масса летательного аппарата, осуществляющего обработку поля от вредителей, может значительно уменьшаться до 30 % и более. Вопросы влияния изменения полетной массы на характеристики и устойчивость полета в исследованиях автоматического управления полетом МБЛА не рассматривались. Ввиду уменьшения массы во время полета коэффициенты дифференциальных уравнений движения МБЛА становятся переменными, применение методов операционного исчисления и передаточных функций требует дополнительных обоснований. В настоящем исследовании изложены результаты, полученные с помощью двух компьютерных моделей автоматического управления полетом: программного и траекторного. Рельеф поля в продольной плоскости полета представлен двумя формами: прямой и волнистой наклонными линиями. В первой модели управление рассчитывалось с помощью дифференциальных уравнений продольного полета МБЛА с переменной массой при задании траекторного угла и скорости центра масс летательного аппарата, во второй – полет моделировался дифференциальными уравнениями движения тела переменной массы с заданием функций управления рулем высоты и тяги двигателя по показаниям датчиков высоты и угла тангажа.

Целью исследования является оценка влияния переменной массы на высоту полета и скорость центра масс МБЛА при их стабилизации в режиме автоматического управления рулем высоты и тягой двигателя.

Задачи исследования включают в себя разработку алгоритма управления летательным аппаратом и компьютерных моделей управления полетом, моделирование в среде программирования Lazarus и в среде визуального моделирования XCOS Scilab, оценку точности управления в условиях изменяющегося рельефа поля.

ОБЗОР ЛИТЕРАТУРЫ

Беспилотные летательные аппараты (БПЛА) можно использовать как важное звено эффективной системы защиты растений от болезней и вредителей. Для этого следует провести исследования зависимости ширины опрыскивания

^® ИНЖЕНЕРНЫЕ ТЕХНОЛОГИИ И СИСТЕМЫ Том 35, № 4. 2025 от высоты полета БПЛА и нормы рабочего раствора [3]. В результате производственно-полевых опытов установлено, что при планировании полетного задания необходимо учитывать высоту обработки, норму внесения рабочего раствора и ширину захвата. Особенно важно соблюдение ширины захвата во время обработки гербицидами, поскольку ошибка может привести к пропускам, перерасходу препарата и гибели растений. По мнению А. Г. Кузнецова, для повышения точности позиционирования и оценки навигационных параметров МБЛА во время полета целесообразно использовать систему технического зрения. При этом алгоритмы обработки видовой информации сложны, трудоемки и затратны по времени их реализации; для навигации МБЛА необходимы средства управления динамикой летательного аппарата и измерения параметров, а также вычислительные средства [4].

В работе А. В. Архипова и С. П. Тимошенкова представлена разработанная математическая модель и описаны проведенные исследования преимуществ адаптированной системы управления углом тангажа БПЛА [5]. Угол тангажа служит управляемым параметром, с помощью которого можно руководить траекторным углом и траекторией полета, также для синтеза системы управления и стабилизации полета МБЛА рекомендуется применять метод бэкстеппинга [6], согласно которому задача разработки закона управления для всей системы разбивается на последовательность соответствующих подзадач до подсистем меньшего порядка. Приведены результаты численного моделирования в среде Matlab движения БПЛА с полученным регулятором, доказывающие устойчивость системы в больших пределах коэффициентов регулятора.

Методы и алгоритмы формирования динамической системы, моделирующей с заданной точностью целевую миссию БПЛА, представлены В. Е. Усачовым и Р. Ч. Таргамадзе [7]. Оценка точности такой модели осуществляется на основе предложенных критериев качества. Управление полетом МБЛА моделируется как в пространстве, так и в вертикальной плоскости. При этом математическая модель БПЛА как объекта управления представляется в виде линеаризованных математических моделей движения БПЛА [8].

В исследовании А. В. Потудинского отмечается наличие широкого диапазона неопределенностей при управлении динамикой полета различных беспилотных летательных аппаратов и предложены методы, обеспечивающие устойчивость управления в условиях неопределенностей [9]. Представляют интерес алгоритмы генерации траектории полета МБЛА через заданные путевые точки [10]. Такие алгоритмы можно использовать при разработке алгоритмов управлении МБЛА по карте поля. Наряду с вопросами управления полетом МБЛА в научной литературе поднимаются вопросы исследований параметров руля высоты и элеронов [11]. Важные для проектировщиков МБЛА исследования поверхностей элеронов и элевонов позволили найти решения, обеспечивающие устойчивость управления полетом МБЛА. С. Ч. Фам, А. Д. Сурковой и М. С. Селезневой предложены алгоритмы управления МБЛА, позволяющие повысить точность позиционирования МБЛА в базовой инерциальной системе за счет коррекции управления

Vol. 35, no. 4. 2025 ENGINEERING TECHNOLOGIES AND SYSTEMS .^Ts по изображениям местности путем сравнения бортовых радиолокационных снимков с эталонными картами [12]. Задачу вывода беспилотного летательного аппарата в заданную точку пространства (в том числе подвижную) необходимо рассматривать аналогично задачам, которые решаются известными методами синтеза системы самонаведения летательного аппарата на цель [13]. На основе разработанного метода синтеза параметров управления БПЛА предложена методика формирования траектории автоматического облета БПЛА заданной запретной зоны полета. В среде Simulink пакета Matlab произведено моделирование полета МБЛА с отслеживанием траектории его движения в пространстве при воздействии внешних сил (например, ветра) и при отработке сигналов управления рулем высоты, направления, отклонением элерона и дроссельной заслонки [14]. Модель корректно отрабатывает воздействия, возвращая МБЛА на прежний курс.

На моделях и экспериментальным путем изучены четыре стратегии управления МБЛА [15]. Две стратегии основаны на управлении с помощью ПИД-регуляторов, третья реализуется на базе линейно-квадратичного регулятора, четвертая – на управлении регулятором, обеспечивающим прогнозирование. Отмечается надежность ПИД-регуляторов и перспективность контроллеров с функциями прогнозирования. Установлено, что в условиях ветра ПИД-регулятор с оптимальными параметрами настройки обеспечивает более эффективное управление БПЛА при посадке в сравнении с ПИ-регулятором [16].

Было проведено исследование сравнительной эффективности нелинейного ПИД-регулятора и регулятора высокого порядка с настройкой скользящего среднего при управлении полетом БПЛА. [17]. Беспилотный летальный аппарат с фиксированными крыльями моделировался в виде системы с восемью степенями свободы, где учитывались колебания шасси и иных элементов конструкции. Эффективность регуляторов изучалась по ударным воздействиям на колеса шасси. Установлено преимущество нелинейного регулятора. В свою очередь, учеными из Нигерии представлен разработанный прототип БПЛА, который может распылять жидкие пестициды или средства борьбы с сорняками на посевы в сельскохозяйственных предприятиях [18]. Это было сделано путем создания полуавтономного квадрокоптера с системой точного сельскохозяйственного опрыскивания, включающей бак, насос, камеру и форсунки. Таким образом, задача эффективного управления БПЛА в виде квадрокоптера остается актуальной. Следует отметить, что полетная масса летательного аппарата не являлась предметом исследований и принималась постоянной, поэтому вопрос о влиянии ее изменения на управляемые переменные, высоту полета и скорость требует изучения.

МАТЕРИАЛЫ И МЕТОДЫ

Объект исследования

Малый беспилотный летательный аппарат является объектом настоящего исследования.

Методы и оборудование

При разработке математической модели были оспользованы методы дифференциальных уравнений, теоретической механики, автоматического управления, численные методы. Конструктивные параметры и материалы объекта исследования и управления взяты из научной работы Р. У. Биарда и Т. У. Маклэйна1.

Процедура исследования

Компьютерное моделирование автоматического управления рулем высоты и тягой двигателя летательного аппарата для стабилизации высоты полета над полем с переменным рельефом осуществлялось в среде программирования Lazarus и в среде визуального моделирования XCOS Scilab.

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ

Постановка задачи и уравнения движения тела переменной массы

Примем следующие допущения: МБЛА имеет плоскость симметрии (рис. 1), два пропеллера вращаются в противоположных направлениях; движением воздушной среды можно пренебречь и считать скорость ветра равной нулю; силы, действующие на МБЛА, симметричны относительно плоскости симметрии (рис. 2); кориолисовы силы инерции, действующие со стороны частиц воздуха на лопасти пропеллеров ввиду осевой симметрии пропеллера и плоскостной симметрии, взаимно уравновешиваются.

В соответствии с принятыми допущениями можно предположить, что движение МБЛА плоскопараллельное, продольное, без крена и рысканья (рис. 3).

Запишем уравнения движения центра масс МБЛА m переменной массы вдоль оси Ox и вращения МБЛА вокруг оси, проходящей через центр масс. В соответствии с уравнением Мещерского уравнение изменения импульса представим в виде равенства разности количеств движения частиц МБЛА в моменты ( t + Δ t ) и t, с одной стороны, и импульса главного вектора внешних сил, действующих на МБЛА за то же время, с другой:

[(m + Am)(uC + AuC) - Am(uC + um)] - [mиC] = FC At, или после приведения подобных членов и деления уравнения на Δt при Δt → 0:

dv       dm

md- = FC+diU где t- время, с; Am - малое изменение массы МБЛА за малое время At, кг (Am < 0, если масса убывает); ΔυС – изменение вектора υС за время Δt; FС – главный вектор внешних сил, действующих на малый беспилотный летательный аппарат; um – вектор скорости частицы рабочего вещества на выходе из форсунок относительно корпуса летательного аппарата.

• a)                                      b)

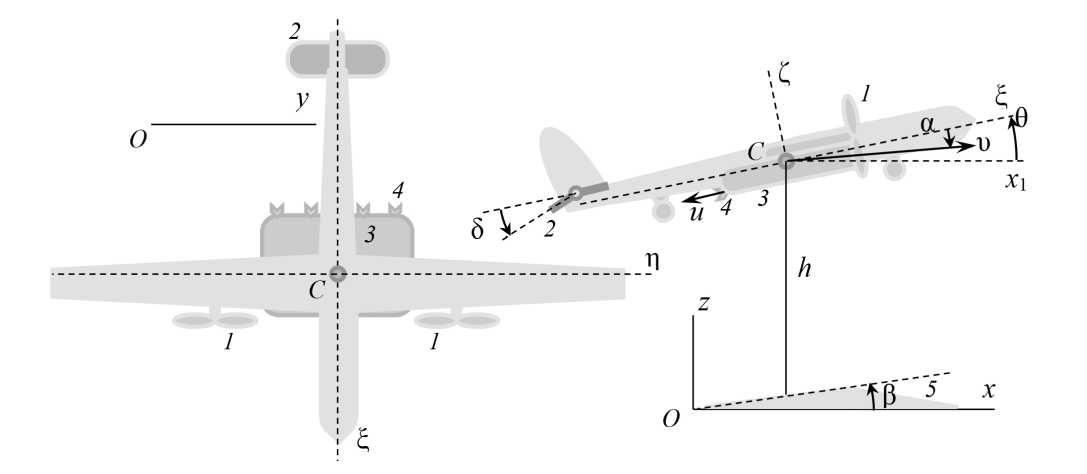
Р и с. 1. Малый беспилотный летательный аппарат при продольном полете без крена:

• a) вид сверху; b) вид сбоку:

• 1    ‒ пропеллеры; 2 ‒ система управления углом тангажа; 3 ‒ рабочая емкость; 4 ‒ форсунки;

5 ‒ прямолинейный участок профиля поля с наклоном под углом β

F i g. 1. Scheme of a small unmanned aerial vehicle in longitudinal flight without roll:

• a) viewed from above; b) from the side:

• 1    ‒ propellers; 2 ‒ elevator actuator; 3 ‒ container with working substance for spraying;

4 ‒ nozzles; 5 ‒ field profile with a rectilinear slope at an angle β

Примечание: Oxyz – неподвижная ортогональная система декартовых координат с началом O на уровне моря, горизонтальными осями Ox , Oy и вертикальной осью Oz , направленной вверх; C ξηζ – связанная с малым беспилотным летательным аппаратом ортогональная система декартовых координат с началом C в центре масс малого беспилотного летательного аппарата, осью C ξ, совпадающей с главной продольной осью инерции малого беспилотного летательного аппарата, перпендикулярной ей осью C ζ в плоскости симметрии малого беспилотного летательного апарата и перпендикулярной обеим этим осям осью C η; Cx ₁ – подвижная горизонтальная ось, параллельная оси Ox ; x , z – координаты центра масс малого беспилотного летательного аппарата (точки C ) в неподвижной системе координат по осям Ox , Oz , м; β – угол наклона средней прямой линии профиля поля в продольной вертикальной плоскости, рад; υ ‒ величина скорости центра масс малого беспилотного летательного аппарата, м/с; α – угол атаки, образуемый продольной осью C ξ и вектором υ или проекцией вектора υ на плоскость симметрии малого беспилотного летательного аппарата, рад; h – высота полета над полем, м; δ – угол поворота руля высоты с отсчетом от нулевого положения, рад; u ‒ величина скорости частиц вещества, распыляемого при обработке поля, относительно корпуса малого беспилотного летательного аппарата в направлении, противоположном направлению продольной оси C ξ ( u > 0), м/с;

Note: Oxyz – a fixed orthogonal system of Cartesian coordinates with the origin O at sea level, horizontal axes Ox, Oy and vertical axis Oz directed upwards; C ξηζ – an orthogonal Cartesian coordinate system with origin C associated with a small unmanned aerial vehicle, axis C ξ, coinciding with the main longitudinal axis of inertia of a small unmanned aerial vehicle, perpendicular to it by the C ζ axis in the plane of symmetry of the small unmanned aerial vehicle and perpendicular to both of these axes by the C η axis; Cx ₁ – movable horizontal axis parallel to the Ox axis; x , z – coordinates of the center of mass of a small unmanned aerial vehicle (point C ) in a fixed coordinate system along the axes Ox , Oz , m; β – the angle of inclination of the average straight line of the field profile in the longitudinal vertical plane, rad; υ – the value of the speed of the center of mass of a small unmanned aerial vehicle, m/s; α – the angle of attack formed by the longitudinal axis C ξ and the vector υ or the projection of the vector υ onto the plane of symmetry of a small unmanned aerial vehicle, rad; h – flight altitude above the field, m; δ – elevator rotation angle measured from the zero position, rad; u – the value of the velocity of particles of the substance sprayed during field treatment relative to the body of a small unmanned aerial vehicle in the direction opposite to the direction of the longitudinal axis C ξ ( u > 0), m/s.

Источник: здесь и далее в статье рисунки составлены авторами.

Source: compiled by the authors of the article.

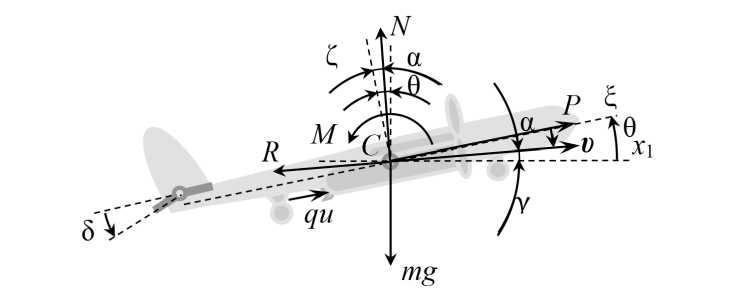
Р и с. 2. Внешние силы, действующие на малый беспилотный летательный аппарат

F i g. 2. External forces acting on the small unmanned aerial vehicle

Примечание: θ – угол тангажа, образуемый осями C ξ и Cx ₁, рад; γ – траекторный угол, образуемый вектором скорости υ и осью Cx ₁ (γ = θ - α), рад; m – масса малого беспилотного летательного аппарата, кг; q ‒ расход рабочего вещества при обработке поля на единицу длины пути вдоль оси Ox , кг/м; P ‒ величина главного вектора сил тяги двух пропеллеров (сила тяги), Н; N ‒ величина главного вектора подъемных сил (подъемная сила), Н; R ‒ величина главного вектора сил сопротивления (сила сопротивления), Н; M ‒ величина главного момента внешних силы относительно оси C η, Н м; g ‒ ускорение свободного падения материальной точки, м/с².

Note: θ – pitch angle formed by the axes C ξ and Cx ₁ , rad γ – trajectory angle formed by the velocity vector υ and the Cx ₁ axis (γ = θ - α), rad; m – mass of a small unmanned aerial vehicle, kg ; q ‒ consumption of working substance during field processing per unit length of path along the Ox axis, kg/m; P ‒ the magnitude of the main vector of the thrust forces of two propellers (thrust force), N; N ‒ the magnitude of the main vector of lifting forces (lift force), N; R ‒ the magnitude of the main vector of resistance forces (resistance force), N; M ‒ the magnitude of the principal moment of external forces relative to the C η axis, N m ; acceleration of gravity of a material point, m/s².

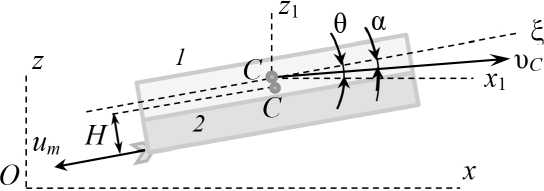
Р и с. 3. Обоснование уравнений движения малого беспилотного летательного аппарата с переменной массой и переменным положением центра масс С :

1 – рабочая емкость; 2 – вещество в рабочей емкости

F i g. 3. To the substantiation for the equations of a small unmanned aerial vehicle motion with variable mass and variable position of the center of mass C :

1 – container; 2 – substance in container

Примечание: υ _С – вектор скорости центра масс малого беспилотного летательного аппарата; u_m – вектор скорости частицы рабочего вещества на выходе из форсунок относительно корпуса малого беспилотного летательного аппарата; H – расстояние от центра масс до линии вектора u_m , приложенного к форсунке в плоскости симметрии малого беспилотного летательного аппарата, м.

Note: υ _С – velocity vector of the center of mass of a small unmanned aerial vehicle; u_m – the velocity vector of the working substance particle at the outlet of the nozzles relative to the body of the small unmanned aerial vehicle; H – distance from the center of mass to the line of vector u_m applied to the nozzle in the plane of symmetry of a small unmanned aerial vehicle, m.

При выходе рабочего вещества из форсунок проекции векторов υС и um на ось имеют противоположные знаки, а производная массы МБЛА по времени – отрицательную величину. Уравнение изменения кинетического момента МБЛА запишем в движущейся системе координат с началом в центре масс МБЛА и осями, параллельными неподвижным осям Ox и Oz. Будем полагать, что частицы рабочего вещества в емкости под давлением вращаются вокруг оси вместе с фюзеляжем. Угловая скорость, кинетический момент и момент внешней силы положительны, если при наблюдении с конца оси согласуются с вращением против хода стрелки часов. Разность кинетических моментов частиц МБЛА относительно оси, проходящей через центр масс МБЛА, перпендикулярной плоскости симметрии, в моменты (t + Δt) и t равна импульсу главного момента внешних сил, действующих на МБЛА, относительно той же оси за то же время:

[(J + ∆ J)(ω + ∆ω) + ∆mHu] – [Jω] = M∆t, где u =|um|; ω ‒ угловая скорость вращения малого беспилотного летательного аппарата вокруг оси Cη, рад/с; Δω ‒ изменение угловой скорости ω за малое время Δt, рад/с; J ‒ текущий момент инерции малого беспилотного летательного аппарата относительно оси Cη, кг∙м2; ΔJ ‒ изменение момента инерции J за малое время Δt, кг∙м2.

После приведения подобных членов, деления обеих частей на Δ t и Δ t → 0 уравнение примет вид:

d ω   djdm

J + ю = M - dt     dtdt и, полагая, что угловая скорость настолько мала, что ей можно пренебречь, получим:

d ω

J — = MHu dtdt

Модель программного управления малого беспилотного летательного аппарата

Программное управление движением определяется как управление желаемым движением и находится из решения уравнений движения. Рассмотрим полет МБЛА на заданной высоте над полем по траектории, параллельной линии профиля поля в продольной вертикальной плоскости полета. Полагаем, что программное управление поддерживает траекторный угол МБЛА равным углу наклона линии профиля поля к горизонту. Неподвижную систему координат выберем так, чтобы плоскость Oxz совпала с плоскостью симметрии C ξζ. При составлении дифференциальных уравнений плоскопараллельного движе-ния² в инерциальной системе координат Oxz уравнение движения (1) центра масс МБЛА запишем в естественном виде, проецируя ускорение точки и силы на ось касательной, направленную по вектору скорости υ центра масс МБЛА, ось нормали к траектории центра масс, направленную в сторону вогнутости траектории. Уравнения движения запишем так:

где

J =

dv            dm m — = P cos a — R--u cos a — mg sin (e — a)

dt                  dt

d ( e — a )                dm .

mv —----- = P sin a + N —   u sin a — dt                     dt jd^ = m — dmHu

dt d e

dt

— = ro dt

— = v cos ( e — a ) dt

— = v sin ( e — a ) , dt

m =

m0 + mc , m0 + mc -q(x-x0),

m 0 ,

mg cos ( e — a )

0 < x < x0 m x0 +--- > x > x0

q

x >  x ₀

m

+—;

q

J 0

+ m c

H

,

0 <  x <  x ₀

J o

+ [ m

c

— q (x — x 0

H .Hq ^ x - x o )

J o ,

>1H+

2 m

c

,

m

x0 +--- > x > x0 q

x >  x ₀

m

+—;

q

0,

dm dt

,               0 <  x <  x 0

-------------1

qv cos ( 0 — a ) , x 0 + m c- >  x > x 0 ^q

0,

m

q где x0 – координата х в момент начала уменьшения массы МБЛА; m0, mc ‒ масса летательного аппарата без рабочего вещества и максимальная масса рабочего вещества (m0 ≤ m ≤ m0 + mc), кг; J0 ‒ момент инерции малого беспилотного летательного аппарата относительно оси Cη без рабочего вещества, кг∙м2.

Уравнения (3) содержат силы P , R , N и пару сил M , выражения для которых определены по экспериментальным данным³. В соответствии с уравнением Бернулли разность Δ p давлений воздуха на выходе из пропеллера при скорости воздуха υ ₀ и на входе в него при скорости воздуха υ определяется по формуле:

AP = 2P(uo -u ), где ρ ‒ плотность воздуха, кг/м3.

Принимая скорость υ ₀ воздуха на выходе прямо пропорциональной перемещению δ _P руля тяги, а силу тяги P прямо пропорциональной разности давлений и площади сечения пропеллера, последнюю формулу для двух пропеллеров получим⁴:

P = pSp [(kp8 p )2 - v2 ]. (4)

где sp ‒ площадь поперечного сечения пропеллера, м2; kp ‒ коэффициент тяги пропеллера, (м/с)/м; δP – перемещение тяги двигателя (дроссельной заслонки), м. При малых углах тангажа и атаки справедливы следующие выражения для сил сопротивления R, N, M 2:

^N = ¹ P v²s . ( c : + c N p P + c N _fS )

-^R = -P v s w ⁽ c R + c R p ^P

• 2          (

M = -Pv swc cMpP + — ® + cM8S , где c, cN , cNα, cNδ , cR , cRα, cMα, cMω, cMδ – экспериментальные коэффициенты; sw ‒ площадь поперечного сечения крыла, м2.

Система уравнений (3) с учетом функций (4), (5) при заданных начальных условиях и заданном законе управления δ(t), δP(t) является замкнутой и позволяет однозначно определить шесть неизвестных, являющихся переменными состояния: υ, ω, α, θ, x, z. Для определения функций управления δ(t), δP(t) необходимо задать два условия (уравнения). Такими являются уравнение профиля поля или соответст-

вующее ему уравнение траекторного угла и задание скорости центра масс МБЛА.

Линию профиля поля с координатами z_f по оси Oz зададим в виде наклонной прямой

линии (верхняя формула) или волнистой наклонной линии (нижняя формула) так:

z f =

x tg P x tg P +

h_c sin

[ 2 n x} [ 250 J

где zf – координата точки профиля поля по оси Oz, м; hс – заданная высота полета над полем, м.

Два условия (уравнения) по траекторному углу γ и скорости υ зададим в виде:

dz   dzf tg (9 — a) = tg у =   = —^

dx dx u = и c = const, где zf – функция от x, заданная формулами (6), υс – заданная скорость, м/с.

Система алгебро-дифференциальных уравнений (3), (7) с учетом (4), (5) состоит из восьми уравнений и позволяет найти шесть переменных состояния и две переменные управления, которые служат программным управлением. Она приводится к линейной системе четырех обыкновенных дифференциальных уравнений с переменными θ, ω, x , z при заданной постоянной скорости υ _c . Действительно, из первого уравнения системы (3) с учетом выражения для R из (5) следует такое равенство:

mg sin P     mm    1 p v C s w [ Cr + Cr _a ( 0 - ^y)]

P =----7-----7 +--U +---7-----7------ cos (0 — y)   mt 2      cos (0 — y)

Используя формулу (4), найдем δ _P :

где Р задается формулой (8).

P

+ v

5 2 = PSp____

P k2 p

C

,

Из выражения (5) для N найдем δ, подставляя в него выражение N из второго уравнения системы (3), в таком виде:

-NT- /- c N - c N a ⁽ 0 - Y )

₅ = P v C s J-------------- ,                     (10)

^C N S

Idm |                              dу где N = u — P sin (0 — у) + mg cos у + mvc — vc cos у.

I dt )    '      '                    ^C dx ^C

Подставляя δ из (10) и α из (7) в выражение (5) для M , получим такую формулу:

M = 1 P ^vC s w c c

^

•M „ ( e - r )+— v _c

® ⁺ c M _S ⁸ .

?

Отмечаем, что последние четыре уравнения системы (3) с учетом выражений (6)–(11) служат системой дифференциальных уравнений с неизвестными θ, ω, x , z . В установившемся режиме полета на участках с постоянной массой угол тангажа и угол атаки зависят от заданной скорости и массы МБЛА и связаны с ними так:

2 mg [cos у - sin у tg ⁽ e - y ^)]_                    _{C;v 8} c_{M a} ⁽ e - y) ,

-------------2------------- = ^CN + ^CN a ^{( e - y )+} +

P v_C s w                                    ^CM 8

^{+ [ C}R + ^CR a ^{( e} - У ) ] tg ^{( e} - У ) .

Отсюда следует, что установившееся значение угла тангажа совпадает с заданным траекторным углом γ, если скорость рассчитывать по следующей формуле:

v

c

2 mg cos у c N P s w

Модель траекторного управления малым беспилотным летательным аппаратом

Программное управление предполагает, что истинный рельеф поля описывается заданной функцией, начальные моделируемые и реальные условия совпадают, погрешность модели отсутствует. Ввиду расхождений по всем позициям программное управление эффективно, если имеются основания считать такие расхождения незначимыми. Вместо уравнений (7) зададим управления в виде: t

• 8 = b 1 ( 9 — p ) + b ₂ ю + c 1 ( z — Z f — h_c ) + c 2 J* ( z — Z f — h_c ) dt ,       (13)

_{t 0}

• ⁸ P = ^k 1 ( v a ^- v ) + k 2 / ( v a ^- v ) ^dt ,                     ⁽¹⁴⁾

Vol. 35, no. 4. 2025 ENGINEERING TECHNOLOGIES AND SYSTEMS-^ где b ₁, b ₂, c ₁, c ₂, k ₁, k ₂ – задаваемые коэффициенты ПИ регулятора для управления рулем высоты и дроссельной заслонкой (тягой двигателя); z_f – функция (6); υ_a – заданное значение скорости.

Вопрос обоснования коэффициентов b ₁, b ₂, c ₁, c ₂, k ₁, k ₂ не рассматривался. Коэффициенты оценивались так, чтобы значения переменных управления не превышали заданных рабочих пределов δ_max по углу поворота руля высоты и δ_Pmax по перемещению дроссельной заслонки (тяги двигателя). Технология подобной оценки приведена, например, в упомянутой выше работе Р. У. Биарда и Т. У. Мак-лэйна⁵. В равенствах (13), (14) предполагается, что значения высоты полета, угла тангажа, угловой скорости и скорости, регистрируемые датчиками и рассчитываемые по уравнениям движения МБЛА, совпадают. Шесть уравнений (3) после подстановки в них выражений (13), (14) для переменных управления содержат все шесть переменных состояния и при заданных начальных значениях переменных и коэффициентах могут быть решены. Уравнения (3) с учетом уравнений (4)–(7), (13), (14) рассматриваются как модель траекторного управления.

Алгоритм расчета высоты и скорости

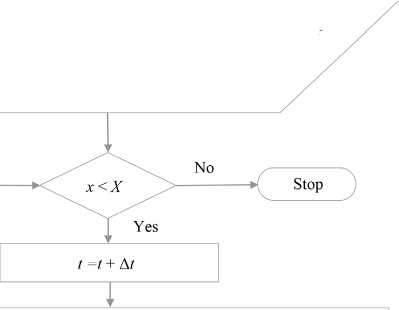
Алгоритм представим в виде блок-схемы (рис. 4).

Ввод данных:

то, т_с, h_c, хо, Jo, Н, п, р, q, Р, g, s_w, s_p, к_р, с, cn, cnu, ем, CR, CRa, С/М, СМа, СМа, С Me, 5max, Зртах, Ъ{, Ьэ, Cl, С2, к{, кэ

Назначение дальности X полета по оси Ох, шага А/ по времени и начальных значений при / = 0 переменных состояния: 0 = Р, о = 0, х = 0, z = hc при программном управлении и 0 = Р, о = 0, х = 0, z = hc, а = 0, о = 20 или 25 м/с при траекторном управлении остановка

/ =/ + А/

При программном управлении решение последних четырех уравнений системы (3) относительно переменных 0, со, х, z методом Рунге - Кутта четвертого порядка с учетом формул (3), (6)-(12) и определение а из первого равенства (7).

При траекторном управлении решение уравнений системы (3) относительно переменных и, а, 0, со, х, z методом Рунге - Кутта четвертого порядка с учетом формул (3), (4)-(6), (13), (14).

Р и с. 4. Упрощенная блок-схема расчета высоты полета в моделях программного и траекторного управления

Data entry:

mo, m_c, h_c, .to, Jo, H, u, p, q, p, g, s„, s_p, k_p, c, cn, cn„, c®, cr, CRu, OR , CMu, CM®, CMS, Smax, Sfmax, Ь\, bl, Cl, Cl, kl, kl

Assigning the flight range X along the Ox-axis, the time step At and the initial values at / = 0 of the state variables 0 = P, = 0, x = 0, c = he under software control and 0 = p, to = 0, x = 0, z = h_c, a = 0, и = 20 or 25 m/s with trajectory control

In program control, the solution of the last four equations of system (3) with respect to variables 0, to, x, z using the fourth-order Runge - Kutta method, taking into account formulas (3), (6)-(12) and determining a from the first equality (7). In trajectory control, the solution of the equations of system (3) with respect to the variables u, a, 0, в, r, z is carried out using the fourth-order Runge - Kutta method, taking into account formulas (3), (4)-(6), (13), (14).

F i g. 4. Simplified flow chart for calculating flight altitude in software and trajectory control models

Компьютерное моделирование

Алгоритм определения значений высоты и скорости был реализован в среде программирования Lazarus и в визуальной среде моделирования XCOS Scilab при следующих исходных данных⁶ m 0 = 13,5 кг; m c = 5 кг; h c = 10 м; x 0 = 600 м; J ₀ = 1,135 кг м²; H = 0,035 м; u = 2,5 м/с; ρ = 1,27 кг/м³; q = 0,007 кг/м; β = 4 град; g = 9,8 м/с²; s_w = 0,55 м²; s_p = 0,11 м²; k_P = 80 (м/с)/м; c = 0,19 м; c_N = 0,8; c N α = 3,45; c N δ = –0,36; c R = ^p 0,03; c R α = 0,3; c M α = –0,38; c M ω = –3,6; c M δ = –0,5; δ_max = π /3; δ _{P max} = 0,04 м; b ₁ = π /3 рад/рад; b ₂ = π /60 (рад·c)/рад; c ₁ = 0,2 рад/м; c ₂ = 0,025 рад/(м·с); k ₁ = δ _{P max}/10 (м·с)/м; k ₂ = δ _{P max}/80 м/м.

Программное и траекторное управления позволили стабилизировать высоту полета над полем с прямолинейным и волнистым рельефом, моделируемым уравнениями (6) (рис. 5).

В случае прямолинейного рельефа траектория центра масс МБЛА становится прямой линией, параллельной линии рельефа. Расчеты и моделирование показали, что программное управление обеспечило стабилизацию скорости и высоты полета над полем с любым рельефом. Изменение полетной массы при

Vol. 35, no. 4. 2025 ENGINEERING TECHNOLOGIES AND SYSTEMS -^ траекторном управлении не изменило высоту полета, если к началу рабочего процесса, во время которого полетная масса начинала уменьшаться, высота стабилизировалась (рис. 6 а).

a)                                           b)

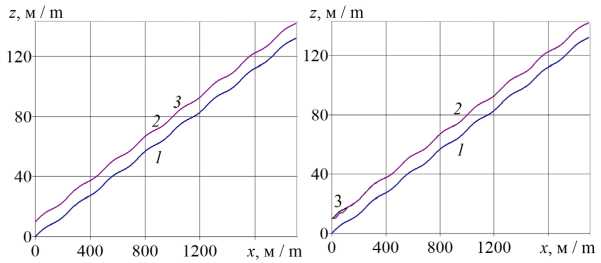
Р и с. 5. Зависимости от координаты x координаты z (высоты над уровнем моря) точек линии волнистого профиля поля 1 и центра масс малого беспилотного летательного аппарата при программном (а) и траекторном (b) управлении при полете с заданной скоростью:

2 – 20 м/с; 3 – 25 м/с

F i g. 5. Depending on the x coordinate of the z coordinate (altitude above sea level) of the points of the wavy profile line of field 1 and the center of mass of a small unmanned aerial vehicle with software (a) and trajectory (b) control when flying at a set speed:

2 – 20 m/s; 3 – 25 m/s

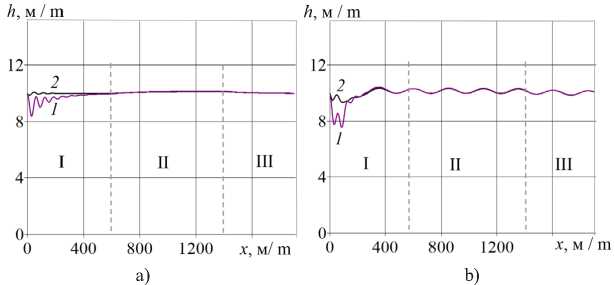
Р и с. 6. Зависимости высоты полета h над полем с прямолинейным наклонным профилем (а) и волнистым наклонным профилем (b) от координаты x при траекторном управлении и заданной скорости:

1 – 20 м/с; 2 – 25 м/с

F i g. 6. Dependence of the flight altitude h above a field with a straight inclined profile (a) and a wavy inclined profile (b) on the coordinate x with trajectory control and a given speed:

1 – 20 m/s; 2 – 25 m/s