Компьютерное моделирование деформированного состояния физически нелинейных трансверсально-изотропных тел с отверстием

Развитие науки и вычислительных технологий на современном этапе позволяют создавать компьютерные модели, реально отражающие картину напряжённого состояния композиционных конструкций. При этом особое внимание уделяется исследованию влияния структурных особенностей волокнистых материалов и концентраторов напряжений. Приближённые методы построения решений статических задач для анизотропной пластинки с криволинейными отверстиями и решения предложены в [1]. В [2] рассматривается плоская задача для пластинок с эллиптическим отверстием и мало от него отличающимся криволинейным отверстием. Изучено напряжённое состояние указанных пластинок при осевых и поперечных нагрузках. Влияние концентраторов напряжений на прочность армированных пластинок изучается в [3], где анализируется напряжённое состояние в окрестности кругового отверстия, расположенного в центре конструкции. Отмечается, что на боковой поверхности кругового отверстия максимального значения достигают касательные напряжения. Так как композит плохо сопротивляется сдвигу, то в зонах, где касательные напряжения максимальны, появляются трещины. В однонаправленном материале эти трещины распространяются вдоль волокон на всю длину образца и приводят к общему разрушению. Но возникновение таких небольших трещин разгружает материал в окрестности круглого отверстия. В [4] проводится исследование концентрации упругих напряжений вблизи кругового отверстия в пластине из бороалюминия с использованием плоской волокнистой конечно-элементной модели, явным образом воспроизводящей структуру материала с сохранением объёмных долей составляющих и характерных структурных размеров в двумерном представлении. Для изучения концентрации напряжений в волокнах и связующем при растяжении вдоль волокон и при сдвиге структура считается волокнистой, составленной из однородных элементов разной жёсткости с размерами, меньшими характерного размера структурной неоднородности.

Разработке моделей и решению задач физически нелинейного деформирования волокнистых композиционных материалов посвящены работы многих авторов, см., например, список цитирования в [5]. В [6] излагаются основные положения (постулаты) механики сплошной среды. Наряду с классическими моделями рассматриваются сравнительно новые модели, где материал — композит, и модели, учитывающие связанность механических полей. Работа [7] содержит результаты экспериментального и численного конечно-элементного определения показателей анизотропного напряжённо-деформированного состояния (НДС) при одноосном растяжении графито-эпоксидных слоистых композитных прямоугольных пластин с однонаправленными подкрепляющими углеродными волокнами, содержащих центральное круглое отверстие. В работе [8] дан анализ концентрации и распределения напряжений в изотропных, ортотропных и слоистых композитных пластинах с центральным круглым отверстием, подвергнутым поперечной статической нагрузке. В работе [9] исследуется влияние концентратора напряжений в прямоугольной пластине. Концентратором является круглое отверстие. Приводятся значения коэффициентов концентрации напряжений в окрестности отверстия, полученные методом конечных элементов. В [10] рассмотрены алгоритм и решение задачи с учётом физической нелинейности тел на основе теории малых упругопластических деформаций. Отмечается, что процесс решения с использованием деформационной теории выполняется значительно быстрее, чем в рамках теории течения.

Известно, что наличие в телах конструкционных отверстий существенно сказывается на деформировании в их окрестности. В [11] на основе уточнённой теории изучено влияние анизотропии материала на деформированное состояние пластины с отверстием и установлены границы пластической зоны. Исследуется вид пластической зоны вблизи круглого отверстия в бесконечной пластине из трансверсально-изотропного материала. Прогнозирование прочности слоистых композитов с отверстиями и повреждениями типа трещин выполнено в [12, 13]. Решение задачи определения напряжённого состояния толстой плиты (случай плоской деформации) из упругого идеально пластического анизотропного сжимаемого материала, ослабленной эллиптическим отверстием, приводится в [14]. Плита находится в условиях двуосного растяжения на бесконечности. Упругопластический анализ напряжений изотропной пластинки в окрестности квадратного отверстия осуществляется в [15]. Границы поля пластических напряжений вокруг конформно-отображаемых квадратных отверстий ищутся с помощью упругих уравнений Г.Н. Савина. Для нахождения численных решений применяется конечно-элементный подход. Сравниваются теоретические и конечно-элементные упругопластические решения для изотропных пластин с квадратными отверстиями, у которых закруглены углы.

В данной работе для описания анизотропии механических свойств трансверсально-изотропных материалов используется структурно-феноменологическая модель, представляющая исходный материал в виде комплекса из двух совместно работающих изотропных материалов: основного материала (связующего) и материала волокон, ориентированных вдоль направления анизотропии исходного материала. При этом связующее рассматривается с позиций механики сплошной среды, а материал волокон — в предположении, что волокна воспринимают лишь осевые усилия растяжения–сжатия и деформируются совместно со связующим. Для решения задачи теории пластичности применяется упрощенная теория малых упругопластических деформаций для трансверсально-изотропного тела [16]. Упрощение заключается в замене исходной волокнистой среды эквивалентной трансверсально-изотропной средой с эффективными механическими параметрами. Вследствие этого при простом растяжении композита в направлении оси трансверсальной изотропии и в направлении, перпендикулярном к ней, пластических деформаций не возникает, интенсивности напряжений и деформаций определяются отдельно как по главной оси трансверсальной изотропии Oz — (Qu,qu), так и в перпендикулярно расположенной плоскости изотропии Oxy — ( Pu, pu). Упрощенная теория малых упругопластических деформаций открывает возможности для решения конкретных прикладных задач. В случае тел с отверстиями она позволяет производить достаточно точный расчёт напряжений и деформаций при различных видах нагружения при условии, что оба размера, характеризующие волокнистый материал — толщина волокна и ширина промежутка между волокнами — на несколько порядков меньше радиуса отверстия [4].

Для вычисления значений эффективных механических параметров волокнистых материалов в работе используются соотношения, полученные на основе асимптотических методов, в которых учитывается также и радиальное взаимодействие компонентов (матрицы и волокна), связанное с различием их коэффициентов Пуассона [17]. Так как деформирование матрицы обеспечивает нагружение высокопрочных волокон, то учёт её пластических деформаций является актуальной задачей, поскольку делает исследование НДС волокнистых композитов наиболее полным [18]. На основе разработанной компьютерной модели деформирования физически нелинейных трансверсально-изотропных тел найдены решения упругих и упругопластических задач деформирования конструкций из волокнистых композитов, и изучено влияние эллиптических отверстий и трещин на интенсивность деформаций пластины.

2.    Постановка задачи и метод решения

Исследуется упругопластическая среда из неоднородного сплошного материала, состоящего из двух компонентов: волокон и матрицы (связующего), которая обеспечивает совместную работу армирующих элементов. Для решения задачи применяется теория малых упругопластических деформаций для трансверсально-изотропной среды [16].

Общая постановка краевой задачи теории упругости для анизотропных тел включает:

– уравнения равновесия

– обобщённый закон Гука

– соотношения Коши

– краевые условия

ст v j+ Xi = о, x ^e v ;

^CT jj = C ijkl ^е kl ;

1 1 d u_k d u l

2 i d x l d x_k

u iL 1 = u^{0 ,}      x i ^1 ,

E ^CT j n l = S^{0 ,}     x i ^e ^ 2

j =1               2

где ui — компонента вектора перемещений; Xi, Sj — объёмные и поверхностные силы; S1, S2 — части поверхности S, ограничивающей объём V ; nj — внешняя нормаль к поверхности S2; Cijkl — тензор упругих констант; сту и еkl — компоненты тензоров напряжений и деформаций.

В упрощенной теории малых упругопластических деформаций трансверсально-изотропной среды обобщённый закон Гука (2) принимает следующий вид:

PQ ст = (X2 +Х4)в + Хзезз, ст33 =Х39 + Х 1£зз, P = -^р Qj= sq-q                     (5)

pu            qu где

P = 2 X ₄(1 -n ( p u )) p u , Q u = 2 X ₅(1 -x ( q u )) q u ,                               (6)

n ( p ) =X 1 ( 1 - pjp ) и x ( q ) = X 2 ( 1 - qs/q ) — функции пластичности типа функций А.А. Ильюшина, значения которых в упругой зоне равны нулю ( X i , p _s и X 2 , q _s — коэффициенты упрочнения и пределы упругой деформации, соответственно, в плоскости изотропии O xy и по оси изотропии O z ). В упругой области параметры CT _tj определяются из закона Гука, а в области пластических деформаций — на основе деформационной теории А.А.Ильюшина; X i — упругие постоянные трансверсально-изотропной среды;

P_ij , Q_ij и p_ij , q_ij — составляющие девиаторных частей трансверсально-изотропных тензоров напряжений и деформаций, соответственно, в плоскости изотропии ( P_ij , p_ij ) и по оси изотропии ( Q_ij , q_ij ):

P u =Л/1 PP =       \(^C 11^{- C} 22^{) 2} + ^4C! 2 ,

P u = 2p P j P j = "У V^(£ 11 -^£ 22 ) ^{+ 4 £} 12 ,

Q u =_x /1 Q j , Q j ^— M ■ cy.

• q u = 2q q j q ij ^— V^£ 13 ^{+ £} 23 ,

причём

Pij = £j + Т (5i38j3 —8j) + £338,38j3 — (£,38j3 + £3j8,3), qj = £i 38 j 3 + £3 j 8 i 3 — 2£338 i 38 j 3, 9 —£11 +£22,

P — c j + c (8i38j3 — 8 y>) + C338i38j3 (c A- = +^3j8i3) ,

Qij — Ci38j3 + C: j8i3 - 2C338i38j3, C — (C11 + C22 )/2 .

Механические параметры трансверсально-изотропного материала связаны с модулями X i следующими соотношениями:

• X, — E ‘(1 — ц)/1, X2 — E (ц + кц2)/[(1 + ц)/1 ], X3 — E ц'/1, X4 — G — Ej [2(1 + ц)], X5 — G', 1 — 1 — ц — 2ц'2 к, к — E/E'.

3.    Вычислительные эксперименты

• 3.1.    Упругий расчёт

Здесь ц и ц' — эффективные коэффициенты Пуассона, Е и E ' — эффективные модули упругости, соответственно, в плоскости и по оси изотропии трансверсально-изотропного материала.

Предполагается, что плоскость трансверсальной изотропии совпадает с плоскостью O xy , а ось изотропии — с осью O z . Поскольку среда является однородной с эффективными механическими параметрами как по оси изотропии, так и по плоскости изотропии, то для решения упругопластических задач используется итерационной процесс метода упругих решений А.А. Ильюшина [19].

Вычислительные эксперименты выполнялись на основе разработанного автором специализированного программного комплекса АРПЭК [20]. Достоверность и корректность предложенной однородной модели подтверждается совпадением результатов, полученных на её основе, с решением ряда тестовых задач на растяжение квадратной пластины с центральным круговым отверстием. В случае упругой задачи результаты по модели автора сравниваются с результатами по волокнистой модели и по модели однородного трансверсально-изотропного материала с эффективными упругими механическими характеристиками бороалюминия [4]. В упругопластическом случае решение сопоставляется с результатами решения задачи растяжения квадратной пластины из волокнистого материала на основе вариационно-разностного метода [6].

Для исследования влияния изолированного отверстия на НДС тела из однонаправленного композита рассматривается трёхмерная упругая задача деформирования прямоугольной пластины (её высота 10 мм, ширина — 5 мм и толщина — 1 мм) при одноосном равномерном растяжении по оси O z распределенной нагрузкой P zz — 100 МПа, приложенной на нижнем и верхнем краях (Рис. 1). Параметры c j определяются из закона Гука, а в соотношении (6) значения функций пластичности п ( p ) и х ( q ) равны нулю. В качестве материала матрицы используется алюминиевый сплав Д16 (дюралюминий) с параметрами: E — 7,1 - 10⁴ МПа (модуль упругости), ц — 0,32 (коэффициент Пуассона), c _s — 2,13 - 10² МПа (предел упругости), p s — 0,003.

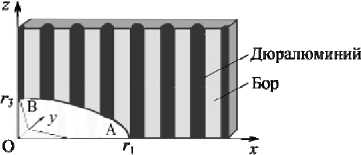
Рис. 1. Четвёртая часть сечения пластины плоскостью O xz

Армирующими элементами служат борные волокна с характеристиками: E ′ = 39,7 ⋅ 10⁴ МПа, µ′ = 0,21 , σ′ s = 2,5 ⋅ 10 3 МПа (предел прочности при растяжении). Волокна материала ориентированы по оси O z , объёмное содержание волокна в композите составляет ν = 60 % , соответствующие эффективные механические параметры бороалюминия следующие: E = 1, 3992 ⋅ 10⁵ МПа, E ′= 2,6682 ⋅ 10⁵МПа, G = 0,6551 ⋅ 10⁵МПА,

G ′ = 0,5396 ⋅ 10⁵МПа, µ= 0,0682, µ′ = 0, 2480 [21].

Путём вычислительного эксперимента исследуется влияние формы отверстия на распределение полей деформаций и напряжений в плоскости трансверсальной изотропии O xy . Варьируются размеры большой ( r ₁ ) и малой ( r ₃ ) полуосей концентратора в форме эллипса. Логически процесс завершается решением упругой задачи растяжения волокнистой конструкции с горизонтальной прямолинейной трещиной в центре. На границе трещины выделяется фронт — плоскость, в которой смыкаются берега трещины. С точки зрения постановки и решения задачи берега трещины играют роль дополнительной границы тела, причём из-за малого расстояния между берегами реальную трещину можно считать математическим разрезом, то есть полостью нулевого объёма, ограниченной двумя геометрически совпадающими поверхностями — берегами разреза. Очевидно, что вблизи фронта будет наблюдаться наибольшая концентрация напряжений, в связи с этим в расчётах окрестность трещины разбивается на более мелкие конечные элементы.

В качестве концентратора рассматривается:

– сквозное отверстие в форме эллипса ( r ₁ = 0,5 мм и r ₃ = 0,1 мм);

– сквозная горизонтальная прямолинейная трещина ( l = 1 мм).

Характерные точки А и В расположены в зонах концентрации напряжений: для эллипса (Рис. 1) — это точка А на пересечении контура отверстия с осью x и точка В на пересечении с осью z ; для трещины: А — в её вершине и В — береговая точка на середине длины.

В таблицах 1 и 2 приведены значения компонент НДС в характерных точках окрестности отверстия в сечении Oxz (u, w — проекции смещения точек, соответственно, на оси Ox и Oz ) в плоскости изотропии Oxy . При r3r1= 0 (случай трещины) интенсивность напряжений Pu в плоскости изотропии повышается, что связано с увеличением разности значений σxx и σyy , а также с возрастанием и сменой

Таблица1. Параметры НДС в точке А пластины с трещиной

r 3 r 1	u ⋅ 10 5 , мм	σ , МПа xx	σ yy , МПа	τ xy , МПа	p u	P u , МПа
4	–0,5710	4,215	5,5695	–0,6092	0,00151	1,972
2	–1,2372	8,684	11,427	–1,0252	0,00266	3,489
4/3	–1,9507	14,250	18,058	–1,3152	0,00351	4,592
1	–2,7033	20,406	25,219	–1,5375	0,00421	5,5225
3/4	–2,6036	32,746	37,874	–1,0085	0,00352	4,6143
1/2	–2,4438	53,186	59,049	–0,1149	0,00317	4,1593
1/4	–1,9935	85,801	94,233	0,9611	0,00500	6,5544
0	–2,060	74,888	30, 862	2,2877	0,00244	32,0307

Таблица 2. Параметры НДС в точке B пластины с эллиптическим отверстием ( τ xy = 0 )

r 3 r 1	w ⋅ 10 5 , мм	σ xx , МПа	σ yy , МПа	p u	Pu , МПа
4	3,0528	–46,102	–12, 586	0,00181	23,705
2	4,3270	–69,287	–13,306	0,00302	39, 595
4/3	5,6192	–78,653	–10,791	0,00366	47,997
1	6,9720	–83,022	–7,9411	0,00405	53,104
3/4	6,4114	–81,179	–7,4131	0,00398	52,174
1/2	5,8184	–80,714	–7,0060	0,00398	52,132
1/4	5,0181	–85,329	–7,6285	0,00419	54,956
0	4,7642	–77,201	–4,4764	0,00393	51,437

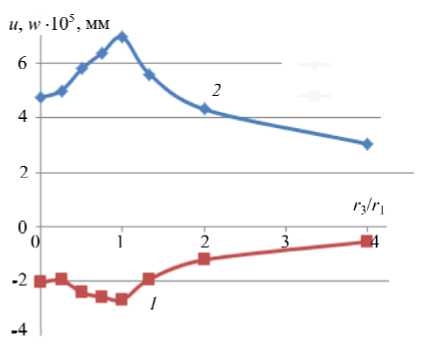
Рис. 2. График изменения смещений u в точке А (кривая 1) и w – в точке В (кривая 2)

знака компоненты напряжения т xy (Табл. 1). Однако значение интенсивности деформаций в плоскости изотропии остаётся вдвое меньшим, чем при наличии отверстия в форме эллипса ( r₃ /г = 1/4) (Табл. 2). Так как трансверсально-изотропная среда является моделью волокнистого композита, то местом наибольшей концентрации разрывающего напряжения становится зона у последнего волокна, обрезанного трещиной. Первое волокно, соседствующее с разорванными, берет на себя основную нагрузку и обеспечивает снижение интенсивности напряжений в местах разрыва волокон [4].

На рисунке 2 показано поведение смещений u в точке А (кривая 1 ) и w в точке В (кривая 2 ). Максимальной величины каждое из них достигает при соотношении r₃ /г 1 = 1, то есть когда отверстие принимает форму круга и имеет наибольшую площадь.

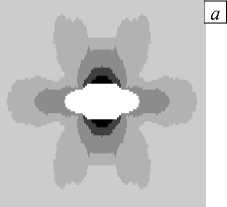
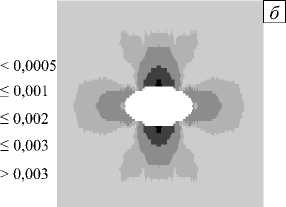
На рисунке 3 приведены распределения интенсивности деформаций pu в плоскости изотропии в сечении Oxz в зависимости от отношения r3r1. Повышенные значения pu локализованы и концентрируются в окрестности отверстия. Под действием растягивающей нагрузки центральная часть конструкции вместе с отверстием сжимается по оси Ox , что подтверждается также наличием сжимающей компоненты напряжения стxx (Табл. 2). Вследствие этого отверстие по оси Oz растягивается.

Рис. 3. Картины распределения интенсивности деформаций p_u в сечении O xz

Повышенные уровни интенсивностей деформаций и напряжений в плоскости изотропии наблюдаются в окрестности верхней и нижней частей отверстия, причём наибольшие значения ( p u = 0,00419 и P u = 54,96 МПа) достигаются при r ₃ = 0,0125 мм. Распределения интенсивности деформаций в трёх вычислительных экспериментах (при отношениях r ₃ / г 1 = 4, 2 и 4/3) подтверждают локальность влияния отверстия на изменение поля интенсивности деформаций: согласно рисунку 3 оно ограничено областями, расположенными в окрестностях верхней и нижней частей контура отверстия.

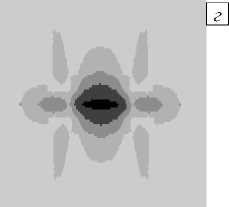
При наличии изолированной прямолинейной трещины (Рис. 4) максимальные значения интенсивности деформаций pu в плоскости изотропии сосредоточены по берегам трещины, а в окрестности вершины её значения несколько ниже.

Рис. 4. Распределение значений интенсивности деформаций p_u в случае трещины

< 0,00005

<0,0001

< 0,0002

< 0,0003

> 0,0003

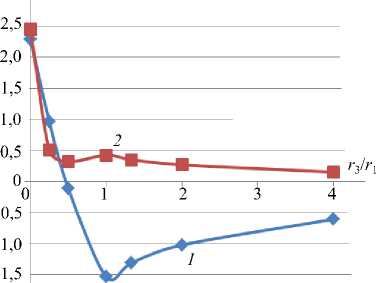
Зоны интенсивности напряжений Pu в плоскости изотропии в окрестности концентратора напряжений при отношении r3r1 из интервала от 1 до 1 8 (при r 1 = 0,05 мм) представлены на рисунках 5а-г. Максимальные значения интенсивности концентрируются вблизи верхней (и, соответственно, не показанной здесь нижней) части отверстия. Однако с уменьшением вертикального размера отверстия около боковых частей также формируются зоны повышенных значений P , что связано u, с увеличением коэффициента кривизны эллипса. Необходимо отметить, что в окрестности

МПа

Рис. 5. Распределение интенсивности напряжений P_u в 1/4 части пластины

точки А значения интенсивности напряжений незначительны. Эта зона отчетливо просматривается на рисунке 5д, отвечающем случаю изолированной прямолинейной трещины.

т_л1, МПа p„- ю⁵

-2,0

Рис. 6. График изменения напряжений т xy

(кривая 1 ) и p_u (кривая 2 ) в точке А

Графики изменения касательной компоненты напряжений т xy и интенсивности деформаций p u в плоскости изотропии в окрестности точки А представлены на рисунке 6. Анализ результатов показывает, что при наличии трещины и сплющенного ( r₃ /г1 = 1/8 ) в направлении оси O z эллипса касательные напряжения положительны. При увеличении значения отношения полуосей r ₃ r ₁ в интервале от 14 и выше касательные напряжения меняют знак на отрицательный и достигают максимального значения при r ₃ / г = 1 (круг). Так как касательные напряжения обычно вызывают изменение формы, то смена знака при уменьшении величины вертикальной оси эллиптического отверстия означает, что в окрестности точки А формируется область максимальных касательных напряжений. Это приводит к появлению трещин, которые распространяются вдоль волокон на всю длину образца и могут привести к общему разрушению конструкции [3].

Для определения зон максимальных тxy при различных соотношениях

касательных напряжений

параметров отверстия проведены вычислительные эксперименты при значениях r ₃ r ₁, приведенных в таблице 2. Результаты экспериментов представлены на рисунке 7. Из рисунка видно, что при значении r ₃ / г 1 = 1 (круг) и меньших в окрестности отверстия формируется стабильная область максимальных т xy .

Рис. 7. Распределение касательных напряжений т xy в 1/4 части пластины

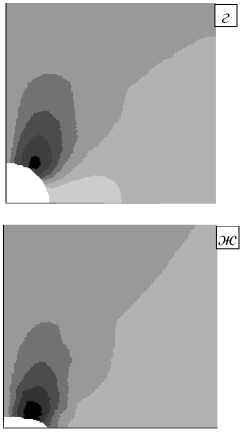
Рис. 7. Продолжение

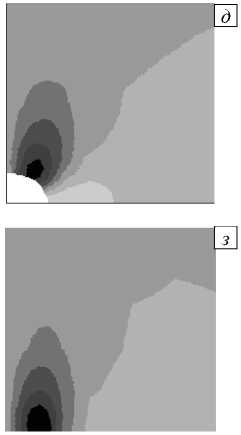
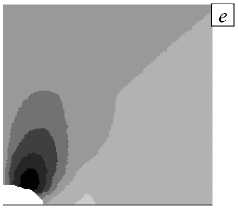
<0,5

МПа

> 1.5

<2,0

>2.0

Рис. 8. Распределение касательных напряжений т xy в случае трещины

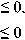
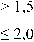
МПа

С уменьшением размера полуоси r ₃ эллиптического отверстия (при постоянном r 1 = 0,05 мм) область максимальных значений охватывает контур отверстия (Рис. 7 а–ж ), а в задаче с трещиной касательные напряжения т xy формируются в окрестностях её вершин (Рис. 7 з ). Именно эти области с точки зрения прочности являются наиболее уязвимыми в волокнистых конструкциях с отверстием или трещиной (Рис. 8), поскольку здесь существует вероятность отрыва матрицы от высокопрочных волокон [3].

• 3.2.    Упругопластический расчёт

Рассматривается трёхмерная упругопластическая задача равномерно распределенного растяжения пластины по оси O z нагрузкой ( P z = 950 МПа), приложенной на нижнем и верхнем краях. В пластине имеется изолированное отверстие в форме эллипса ( r₃ /г1 = 1/8) или прямолинейная горизонтальная трещина. Геометрические и механические параметры задачи идентичны параметрам задачи при упругом расчёте. В первом приближении эффективные материальные константы функции пластичности эквивалентной трансверсально-изотропной среды приравниваются материальным константанам матрицы из дюралюминия. В последующих исследованиях планируется уточнение полученного решения упругопластической задачи.

Для сравнения результатов в таблицах 3 и 4 приведены значения компонент упругого и упругопластического состояния пластины в плоскости трансверсальной изотропии O xy для сечения O xz , характеризующие поведение материала матрицы волокнистых композитов.

Таблица 3. К сравнению параметров при различно вычисленных НДС в точке В пластины с эллиптическим отверстием ( т xy = 0 )

Расчёт	p u	с xx , МПа	с „ , МПа	P МПа u ,
Упругий	0,00398	–810,63	–72,47	522,09
Упругопластический	0,00327	–622,23	–105,28	410,95

Таблица 3 содержит значения параметров НДС в плоскости изотропии в окрестности точки В эллиптического отверстия. Анализ данных указывает на существенное уменьшение значений интенсивности деформаций p_u и напряжений P _u в плоскости изотропии за счет пластических деформаций.

Далее анализируются результаты расчёта НДС пластины с вырезом в форме горизонтальной прямолинейной трещины (Табл. 4). В окрестности срединной точки на берегах трещины значения

Таблица 4. К сравнению параметров при различно вычисленных НДС в пластине с трещиной

	На вершине трещины (точка А)		В срединной точке (точка В)
	упругость	упругопластичность	упругость	упругопластичность
pu	0,00232	0,00155	0,00373	0,00338
a xx , МПа	711,44	492,22	–733,41	–634,13
a„ , МПа	293,19	221,15	–42,526	–72,61
Pu , МПа	304,29	203,10	488,65	418,18

p в пластине u упругом (а, в) и

интенсивности деформаций p u >  p s (пластичность) в плоскости изотропии, однако в окрестностях вершин трещины значения p u <  p s (упругость). Этим подтверждается, что при растяжении волокнистого композита вдоль оси трансверсальной изотропии O z область пластических деформаций в плоскости изотропии концентрируется в окрестностях середины берегов трещины, а в окрестностях вершин трещины область остаётся упругой.

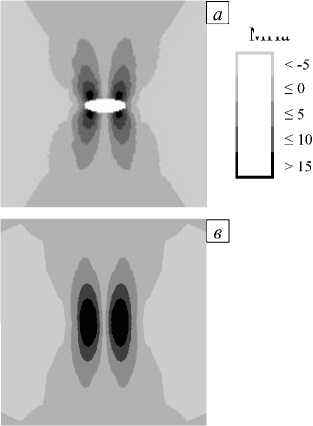
На рисунке 9 приведены распределения интенсивности деформаций p_u в плоскости

Рис. 9. Распределения интенсивности деформаций с эллиптичеким отверстием ( а , б ) и трещиной ( в , г ) в упругопластическом ( б , г ) случаях

(Рис. 9 а , в )  и упругопластического расчётов

изотропии для пластины с отверстием в виде эллипса при r ₃ / r 1 = V8 и с трещиной,

полученные из упругого

(Рис. 9 б , г ). Области пластических деформаций

концентрируются в окрестности верхней и нижней частей эллипса (Рис. 9 б ) и возле середины берегов трещины (Рис. 9 г ).

МПа

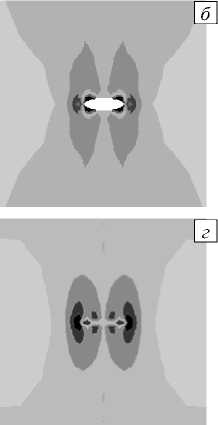
Рис. 10. Распределение касательных напряжений т xy в пластине с эллиптичеким отверстием ( а , б ) и трещиной ( в , г ) в упругом ( а , в ) и упругопластическом ( б , г ) случаях

В завершение приведены распределения касательной компоненты тензора напряжений т (Рис. 10, 12). Анализ полей указывает на то, что, в отличие от упругого случая (Рис. 10 а ), при упругопластическом расчёте происходит перераспределение напряжений: максимальные значения концентрируются в окрестности боков контура эллиптического отверстия и на некотором расстоянии от него (Рис. 10 б ).

Такое же перераспределение можно наблюдать и при наличии центральной горизонтальной прямолинейной трещины (Рис. 10 в , г ). Максимальные значения касательной

компоненты напряжений    т xy

формируются в окрестностях

вершин

трещины.

В упругопластическом случае максимальные значения этой компоненты концентрируются непосредственно у вершин трещины (Рис. 10 в ).

Таким образом, вычислительный эксперимент дает возможность исследовать влияние формы отверстий на НДС конструкций из волокнистых композитов, определить зоны образования пластических деформаций и локализацию областей с максимальными касательными напряжениями, вызывающими отрыв волокна от матрицы. Результаты упругопластического расчёта позволяют уточнить напряжённо-деформированное состояние конструкций и оценить истинное поведение волокнистых композитов.

4.    Заключение

В результате теоретических исследований и проведенных вычислительных экспериментов выполнено следующее:

• 1.    Разработана компьютерная модель решения трёхмерных задач упругого и упругопластического деформирования трансверсально-изотропной среды на основе упрощенной теории малых упругопластических деформаций трансверсально-изотропных сред и метода конечных элементов.

• 2.    Изучено влияние формы отверстий на НДС и распределение интенсивности деформаций в плоскости изотропии в окрестности концентратора напряжений трансверсально-изотропного тела.

• 3.    Определены области пластических деформаций в плоскости изотропии и перераспределение параметров НДС трансверсально-изотропного тела в окрестности концентраторов напряжений.

• 4.    Посредством вычислительного эксперимента для различных конфигураций отверстий в трансверсально-изотропном теле установлено месторасположение областей с максимальными значениями касательных напряжений τ xy , где возможен отрыв высокопрочных волокон от матрицы.