Компьютерное моделирование динамики бионического плавающего робота

Расчетная схема и математическая модель динамики бионического плавающего робота. В качестве расчетной схемы для построения математической модели перемещения бионического плавающего робота в горизонтальной плоскости примем трехзвенную кинематическую схему (рис. 1).

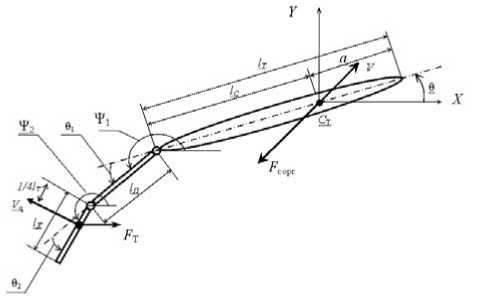
Рис. 1. Расчетная схема бионического плавающего робота в горизонтальной плоскости

На схеме приняты следующие обозначения: X-Y – прямоугольная абсолютная система координат; l T – длина «тела» робота; l П – длина хвостового стебля; l _Х – длина хвостового плавника; С Т – точка, соответствующая центру масс «тела» робота; V – вектор абсолютной скорости центра масс; V q – вектор линейной скорости точки хвостового плавника, отстоящей на расстоянии 1/4 его длины от оси вращения; θ – угловая координата центральной продольной осевой линии тела робота; θ 1 и θ 2 –относительные углы поворота хвостового стебля и хвостового плавника соответственно вокруг своих осей вращения;

ψ₁ и ψ₂ – абсолютные угловые координаты положения хвостового стебля и хвостового плавника соответственно; F Т - вектор силы тяги, возникающей при движении хвостового плавника; F copr – вектор силы сопротивления движению тела робота.

«Тело» робота-рыбы так же, как и хвостовой плавник будем считать плоскими недефор-мируемыми пластинами. В качестве обобщенных координат рассматриваемой системы примем [X,Y,θ,ψ 1 ,ψ 2 ]. Относительные угловые координаты поворота хвостового стебля θ₁(t) и хвостового плавника θ 2 (t) на первой стадии исследования выступают как задающие движение робота, т.е. считаются кинематически заданными. Тогда абсолютные координаты ориентации хвостового стебля и хвостового плавника определяются выражениями

V1( t) = 6( t) + п + 01( t),          (1)

V ₂( t ) = V ₁ ( t ) + 0 2 ( t ) = 6 ( t ) ■ П ■ 6 ( t ) + 6 2 ( t ) .                                                    (2)

Принятая расчетная схема соответствует окунеподобному стилю плавания [2-4], при котором в формировании тягового усилия участвует треть длины тела совместно с хвостовым плавником. Окунеподобный стиль движения является одним из наиболее легко реализуемых в механических аналогах гидробионтов. Кроме того, он является эффективным как с позиций обеспечения высоких линейных скоростей плавания, так и с позиций достаточно высокой степени маневренности. В качестве допущений примем, что масса робота распределена по его «телу», а хвостовой плавник и хвостовой стебель являются безинерционными. Также примем, что силы сопротивления хвоста и силы тяги «тела» пренебрежимо малы по сравнению с силами сопротивления «тела» и силой тяги, приложенной к хвостовому плавнику. Используя положения аэродинамической теории крыла, подъёмную (тяговую) силу, действующую на движущуюся плоскую пластину, можно определить согласно следующему выражению [4]:

uur     uururuur

FT   ПРS (vq X le ) X vq

где ρ – плотность среды (воды); S – площадь по- uur верхности пластины; vq – вектор скорости точки пластины, находящейся на расстоянии четверти её длины от оси вращения (см. рис. 1); le – единичный вектор, расположенный в плоскости пластины и определяемый координатами

le, t = [- c0s(V 2) — sin(V2),0]

uur

Координаты вектора скорости v опреде-q ляются следующими выражениями

V qX ⁽ t ) = ^VX ^{+ L}cort sin [ ^{( 6 (} t ) ]^{6 (} t ) — ^Lp sin [ V 1 ⁽ t ) ]^V 1 ⁽ t ) ^- L Sin [ V 2 ⁽ t ) ] ^V 2 ⁽ t )

V qY ( t ) = V y + L cort cos [ ( 6 ( t ) ] 6 ( t ) - L p cos [ V 1 ( t ) ]x v i ( t ) - L cos [ v ₂( t ) ]\ V ₂( t )

V qZ ( t )     0.                       (7)

Тогда проекции вектора силы тяги F T на оси X и Y в соответствии с (3) - (7) с учетом двойного векторного произведения векторов будут иметь вид

FTX (t) = nPS [VqX (t) sin [ V2 (t)] — VqY (t) C0S [ V2 (t)]] VqY (t)

,

FTY (t) = ПРS [-VqX (t)sin [V2(t)] + VqY (t)c0S [V2(t)]] VqX (t)

Относительные движения хвостового стебля θ 1 ( t ) и хвостового плавника θ 2 ( t ) будем задавать по гармоническим законам

6 ₁( t ) = a ₁sin( o t ) 6 ₂( t ) = a ₂sin( o t ) (ю)

Положение «тела» робота-рыбы зададим параллельным оси X (θ=0) головой вправо, а хвостом – влево. Тогда абсолютные угловые координаты ψ 1 (t) и ψ 2 (t) будут определяться выражениями (1) и (2) с учетом (10). Помимо силы тяги на хвостовую пластину будет действовать момент, определяемый выражением [3, 4]:

Mt = -пр

L (                  1 2

-7 xтУ m cos⁽²V 2 ⁽ t ) + т( У m

4 V                 2

— x & m ) sin⁽² V 2 ⁽ t )

где xm,ym - проекции вектора скорости средней точки хвостовой пластины на оси X и Y, определяе- мые аналогично (6) и (7).

На тело робота-рыбы будут также действовать момент от вектора силы тяги, сила сопротивления жидкости и момент сил вязкого сопротивления. Для определения последних двух факторов необходимо интегрирование распределенных по поверхности тела робота-рыбы сил. Для предварительных расчетов будем считать эти силовые факторы пропорциональными соответствующим обобщенным скоростям

F soprX = ^R X V X F soprY = И Y V Y ^M sopr = ^R 6 ⁶ ,   ,.

Момент, действующий на тело робота, от силы тяги относительно его центра масс, определим в соответствии с векторным произведением

M e ( F t ) = [ X_cq , Y_cq ] ^x [ F tx , F ty ]

где Хcq, Ycq – координаты вектора, связывающего центр масс тела робота-рыбы т. СТ и точку приложения силы тяги на хвостовом плавнике. В результате получим:

M e ⁽ F T ) = ^Ycq^FTX  XcqFTY

Тогда система алгебро-дифференциальных уравнений, описывающих динамику рассматриваемой системы, будет иметь вид:

^m X ^X = ^F TX ^{( X} , ^Y , ⁶ , V 1 , ^ 2 ’ t ) ⁺ F sopr ^{( X} );

m_tY^& = F ty ( X , Y , 6, V i , V 2 , t ) + F sopr ( Y & );

< 1 6 6 = M e ( F t ) + M sopr (6) + M t ( X , Y & ,6,V i ,V 2 );

V i ( t ) = п + 6( t ) + 6 i ( t );

V 2 ( T ) = V i ( t ) + 6 2 ( t ).

Входящие в систему уравнений (15) выражения определяются формулами (8-12), (14). Величины приведенных масс робота m tX и m tY должны быть определены с учетом эффекта присоединенных масс жидкости, участвующей в движении. Обеспечивающие движение робота-рыбы функции относительных углов поворота хвостового стержня θ₁( t ) и хвостового плавника θ₂( t ) будем задавать в виде тригонометрических функций (10). Причем заданием дополнительного определенного угла θ 1 ( t ) представляется возможным выполнять поворот корпуса робота-рыбы.

Математическое моделирование динамики бионического плавающего робота. Математическое моделирование динамики плавающего робота-рыбы рассматриваемой конструкции будем осуществлять в среде имитационного компьютерного моделирования Simulink/MatLab [5]. Основная Simulink-программа компьютерного моделирования динамики робота-рыбы в соответствии с системой уравнений (15) представлена на рис. 2. Расположим составные элементы трехсекционного робота-рыбы горизонтально вдоль оси X головой вправо, т.е. вектор начальных координат рассматриваемой системы будет равен [ X 0 , Y ), 6 0 , V io , V 20 ] = [ 0,0,0, п , п ] , и зададим движение хвостового плавника.

На рис. 3 представлен годограф вектора силы тяги, создаваемой угловым колебательным движением хвостового плавника с амплитудой α 2 =0,3 рад. и частотой ω 2 =2 с^-1 по закону θ 2 ( t ) =α₂sin (ω₂t) при неподвижном состоянии хвостового стебля θ 1 (t)=0 и значениях параметров S =0,02 м², L T =0,2 м, L P =0,1 м, L c ort =0,3 м.

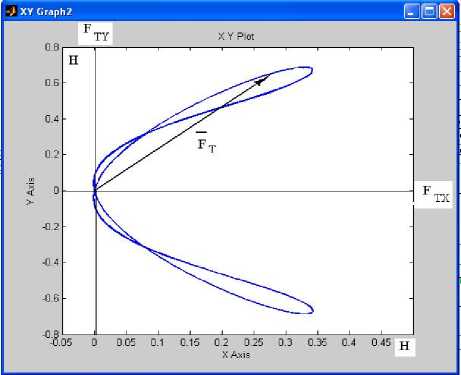
Рис. 3. Годограф вектора силы тяги, создаваемой угловым колебательным движением хвостового плавника

Как следует из анализа рис. 3, годограф вектора силы тяги имеет симметричное расположение относительно оси X, описывая за период колебательного движения хвостового плавника некоторую петлю в I и IV квадрантах. Следовательно, пульсации силы тяги на вертикальную ось Y за период взаимно компенсируются, а горизонтальные составляющие за каждый полупериод положительны и будут обеспечивать продвижение робота вперед (т.е. вправо) вдоль его центральной оси. На рис. 4 представлена траектория движения робота-рыбы в горизонтальной плоскости за 50 с, а изменения самих обобщенных координат во времени, определяющих движение и ориентацию тела робота, даны на рис. 57. Средняя скорость направленного вдоль оси X перемещения составила 0,176 м/с, а само перемещение – более 8 м. Некоторая волнистость траектории носит вполне закономерный характер и вызвана колебаниями тела робота в поперечном основному движению направлении из-за углового колебательного движения хвостового плавника.

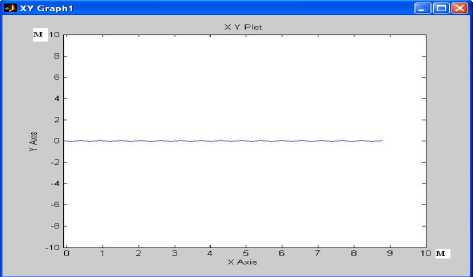
Рис. 4. Траектория движения робота-рыбы в горизонтальной плоскости за 50 с

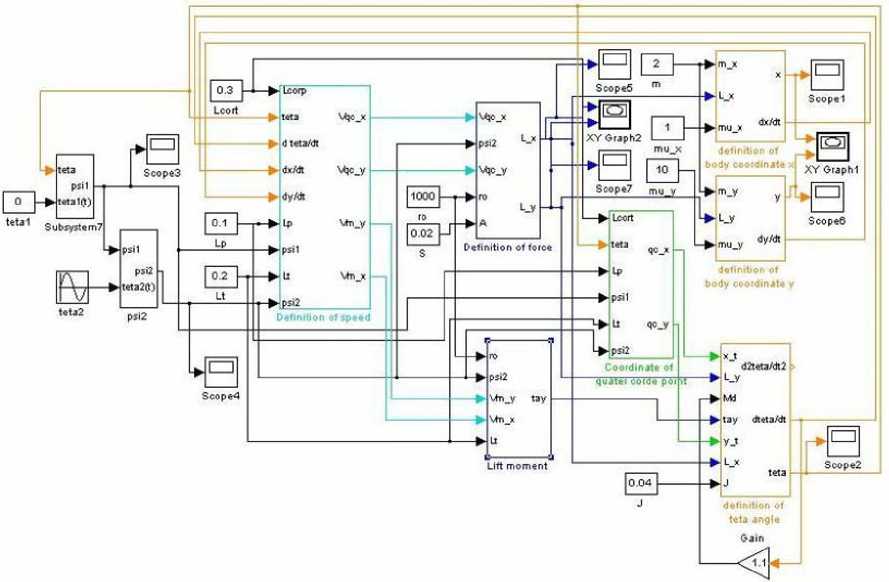
Рис. 2. Simulink-программа компьютерного моделирования динамики робота-рыбы

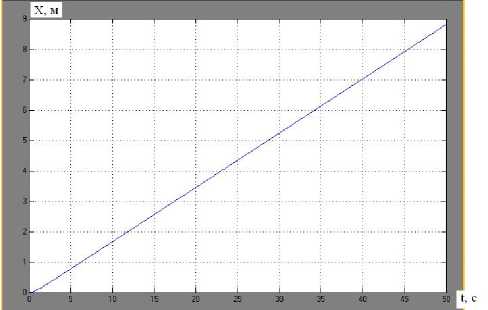
Рис. 5. График изменения во времени перемещения центра масс робота-рыбы по оси X

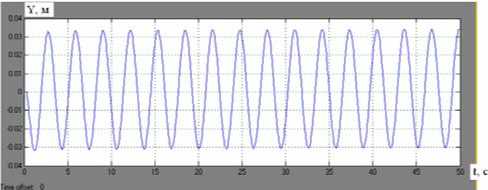
Рис. 6 . График изменения во времени перемещения центра масс робота-рыбы по оси Y

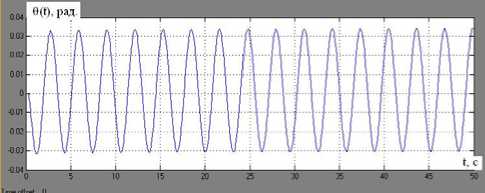
Рис. 7. График изменения во времени углового перемещения тела робота-рыбы θ(t) относительно положительного направления оси X

Рассмотрим теперь траекторию полного разворота корпуса модели робота-рыбы из состояния покоя, задав закон изменения относительного угла поворота хвостового стебля в виде θ 1 ( t ) =α 1 sin(ω 1 t) при значениях параметров α 1 =1 рад, ω 1 =0,5 с^–1 и α 2 =0,3 рад ω 2 =1 с^–1. Полученная траектория движения представлена на рис. 8. Форма траектории обусловлена законом управления относительного угла отклонения хвостового стебля от главной оси тела робота-рыбы. Для обеспечения другой требуемой траектории необходимо задавать некоторый другой закон θ 1 ( t ) или корректировать его в зависимости от положения корпуса робота.

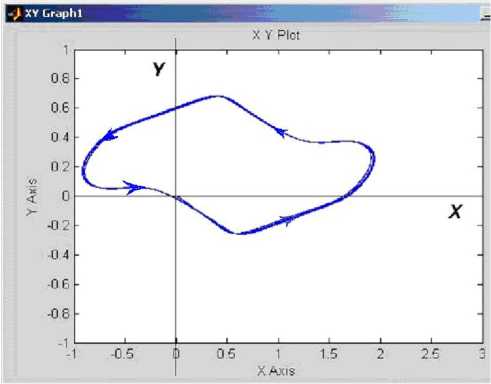
Рис. 8. Траектория разворота на 180º робота-рыбы в горизонтальной плоскости за 80 с (θ 1 ( t )=α 1 sin(ω 1 t), α 1 =1 рад, ω 1 =0,5 с^–1, α 2 =0,3 рад ω 2 =1 с^–1)

Поставим задачу разворота корпуса робота-рыбы в процессе «прямолинейного» движения на 180º. С этой целью зададим закон изменения относительного угла поворота хвостового стебля в виде полуволны синусоиды (рис. 9). Траектория такого движения и разворота на 180º робота-рыбы за 80 с при значениях параметров α 2 =0,3 рад., θ 1 (t)= var, ω 2 =1 с^–1 представлена на рис. 10. Как видно из анализа полученной траектории, разворот корпуса происходит с малым радиусом, без существенного заноса и искажения траектории.

Таким образом, полученные результаты моделирования движения робота-рыбы при различных задаваемых законах управления свидетельствуют об адекватном поведении исследуемой системы и подтверждают правильность разработанной математической модели и функционирования вычислительного программного комплекса для ее решения.

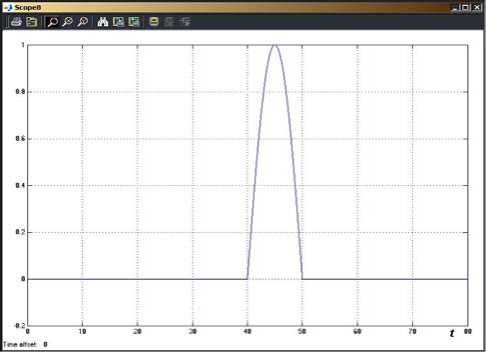
Рис. 9. Закон изменения во времени относительного угла θ₁(t) хвостового стебля, обеспечивающий разворот модели робота-рыбы на 180º

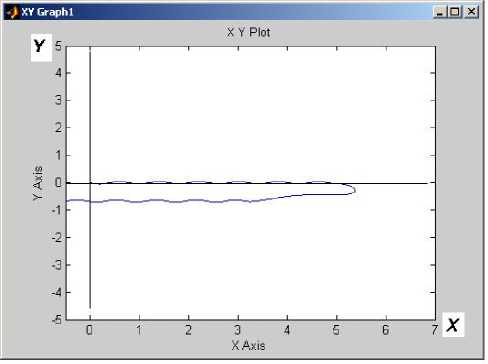
Рис. 10. Траектория движения и разворота на 180º робота-рыбы в горизонтальной плоскости за 80 с (α 2 =0,3 рад., θ 1 (t)= var, ω 2 =1 с^–1)

Выводы: полученные траектории движения, и законы изменении обобщенных координат качественно соответствуют результатам, полученным в работах [2-4]. Конкретные значения коэффициентов сопротивления и других констант дифференциальных и алгебраических уравнений, используемых в данной модели, должны быть уточнены из специально поставленных экспериментов для конкретного прототипа робота-рыбы. Разработанная математическая модель и вычислительный программный комплекс позволят решать задачи оптимизации параметров конструкции разрабатываемого робота и ее системы управления.

Работа выполнена в рамках реализации Федеральной целевой программы «Научные и научнопедагогические кадры инновационной России» на 2009-2013 годы по проблеме «Разработка бионического плавающего робота для мониторинга природных и техногенных объектов в гидросфере» (гос. контракт № П971) .