Компьютерное моделирование потока крови при наличии сосудистых патологий

В настоящее время методы компьютерного моделиро в ания широко используются в исследованиях процесса гемодинамики [3]. Основная трудност ь при этом состоит в сложной внутренней структуре к р ови, а также в сложной структуре пульсирующего потока крови в артериях. Как известно, кровь состоит из плазмы, содержащей 93 % воды, и клеток крови (форменных элементов) – эритроцитов, лейкоцитов, тромбоцитов и моноцитов. Строго говоря, кровь представляет собой двухфазную среду, при этом она включает в себя деформируемые частицы со сложной внутренней структурой, механические свойства которых, к сожалению , мало изучены. Это не позволяет использовать известные модели двухфазных сред, и отдельные попытки описания крови как двухфазной среды содержали значительные упрощения [13, 20]. Наибольший относительный объем в составе крови составляют эритроциты (около 46 %), которые в значительной степени влияют на свойства крови и на структуру потока. В частности, эритроциты ми г рируют по поперечному сечению, смещаясь ближе к оси сосуда. Тромбоциты, напротив, смещаются к стенке сосуда. Кроме того, эритроциты могут образовывать временные агрегаты в виде так называемых «монетных столбиков» (рис. 1), что та к же изменяет структуру потока и его свойства [18]. Особое внимание этому эффекту было уделено в р аботе [4]. Это обстоятельство свидетельствует о том, что кровь можно, хотя и с оговорками, рассматривать как жидкость тол ь ко в тех сосудах, диаметр ко т орых намного больше не только самих клеток, но и их а грегатов, причем жидкость должна обладать неньютоновскими свойствами, чтобы учесть, хотя бы частично, специфические свойства крови. Влияние неньютоновских с в ойств к рови исследовалось, в частности, в работе [11]. В работе [7] проводилось численное исследование неньютоновского потока крови в зоне бифуркации. На н еньютоновские свойства крови обращалось внимание и при моделировании течения крови в зонах сосудистых патологий. Так, в [8] анализировалось влияние неньютоновской вязкости на поток крови в больных артериях, однако лишь для стационарного случая. В работе [19] исследовалось взаимодействие неньютоновского потока с пористой бляшкой.

Следует, однако, отметить, что для неньютоновских жидкостей существует около двух десятков конкретных моделей, в которых формулируется соответству ю щий закон, связывающий тензор напряжений с тензором скоростей деформации. Поэтому адекватность модели в сильной степени зависит от выбора этого закона.

Наиболее полный обзор работ, посвященных различным аспектам моделирования, приводится в работе [5].

Рис. 1. Образование «мо н етных столбиков»

Что касается кровеносных сосудов, то следует отметить, что их механические свойства варьируются в широких пределах. В частности, стенки аорты являются достаточно жесткими и их можно считать недеформируемыми [14, 21]. По мере удаления от сердца стенки сосудов становятся все более мягкими и их деформируемость увеличивается. Однако для некоторых сосудов при решении ряда задач все еще сохраняется возможность не учитывать их деформируемость [10, 12, 15, 16]. В противном случае приходится прибегать к гидроупругой постановке задачи [22].

С учетом вышесказанного целью представленной работы было построить математическую модель течения крови в окрестностях сосудистых патологий, которая учитывала бы в должной мере неньютоновские свойства крови, пульсовый характер ее течения и специфику взаимодействия плазмы и клеток крови со стенкой сосуда.

Модели потока крови и сосудистых патологий

В качестве объектов моделирования были выбраны четыре вида сосудистых патологий: мешотчатая аневризма, фузиформная аневризма, стеноз и бляшка. Как и в приведенных выше работах, стенки сосудов считались недеформируемыми.

Кровь рассматривалась как неньютоновская жидкость, для которой уравнение неразрывности и уравнение движения можно записать следующим образом div v = 0,                                       (1)

P — = V- ( - p I + T ),                             (2)

dt где v – скорость жидкости; ρ – плотность; p – давление; I – единичный тензор и T – тензор напряжений.

В качестве конкретного реологического соотношения был выбран степенной закон зависимости тензора напряжений от тензора скоростей деформаций, а именно

Г n - 1 )

T = 2 k\T 2 |lJ D ,                                          (3)

где I ₂ – второй главный инвариант тензора напряжений; k и n – кэффициенты ( n > 1), являющиеся параметрами модели; D – тензор скоростей деформации. Этот закон примечателен тем, что он способен описывать реологические свойства не только жидкостей, но и суспензий.

В качестве начальных условий для решения уравнений (1) и (2) при выполнении соотношения (3) выбирается состояние покоя при постоянном давлении, т.е.

v t = 0 = ⁰ и p\_t = 0 = p 0 -                                      ⁽⁴⁾

После того как процесс вычислений интересующих нас величин запускается, он продолжается до достижения устойчивого режима.

Для задания граничного условия на входе в рассматриваемый участок артерии было предложено задавать пульсирующее распределение скорости по поперечному сечению в виде части параболоида вращения (рис. 2). Высота этой части параболоида меняется во времени от нуля до максимального значения v _max так, чтобы суммарный поток крови через это поперечное сечение в каждый момент времени был равен потоку, определяемому при клиническом обследовании пациента,

В цилиндрической системе координат r , φ, z это граничное условие можно записать следующим образом:

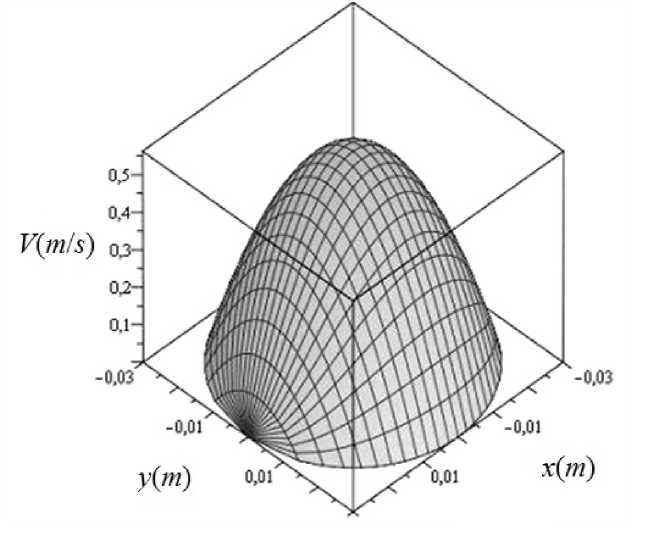
Рис. 2. Пространственное распределение скорости на входе r2

v ( М ) вх = - v max ( t ) ⁽ 2 + 1),                                ⁽⁵⁾

r ₀

где r 0 – радиус сосуда.

Для задания граничного условия на противоположном конце используется известный прием. Выходное поперечное сечение мысленно располагается настолько далеко, чтобы скорость и давление на нем были постоянными.

v | вых = v cp = const и p\ вых = P 0 = const,                           ⁽⁶⁾

где p ₀ – средняя скорость потока.

Во-первых, такой подход оправдан, поскольку пульсовой характер течения ослабевает по мере удаления от сердца. Во-вторых, в этом случае не происходит «навязывания» характера распределения скорости и давления на реальном конце рассматриваемого участка.

При определении граничного условия на стенке сосуда следует отметить, что необходимо учитывать взаимодействие со стенкой не только плазмы крови, но и содержащихся в ней клеток крови. Известно, что стенка сосуда изнутри выстлана однослойным пластом из клеток эндотелия, через который осуществляются обменные процессы. Этот слой и препятствует оседанию доминирующих в пристенном слое тромбоцитов на стенках сосудов, а тромбы образуются в местах разрушения эндотелия. В противном случае упомянутые обменные процессы были бы блокированы, тромбоциты образовали бы сплошной слой нарастающей толщины. В результате жизнь новорожденного продолжалась бы несколько часов.

Сомнения в справедливости условий прилипания для кровеносных сосудов высказывались еще С.А. Регирером и его коллегами [1, 2]. В работе [6] условия полупроскальзывания также предлагается использовать в качестве граничного условия при моделировании потока крови. Следует также отметить, что это граничное условие применяется и для других случаев течения жидкостей [9, 23], в том числе идеальных

[17, 24, 25].

Существует несколько видов аналитического задания условия частичного проскальзывания. Мы использовали линейный случай такого задания:

v wall

dv

= b dy

В этом случае продольная составляющая скорости уменьшается при приближении к стенке сосуда до некоторого наперед заданного значения v0 (рис. 3), которое и является граничным условием на стенке, т.е.

v ( ^r0 , Ф, t ) = v 0 •

Степень полупроскальзывания характеризуют параметром b , который является расстоянием от стенки до точки пересечения касательной к огибающей линии профиля скорости с осью y , как показано на рис. 3.

Таким образом, система дифференциальных уравнений (1) и (2) с учетом соотношения (3) в сочетании с начальными (4) и граничными условиями (5), (6) составляет математическую постановку задачи о течении пульсирующего потока крови.

Для построения механических моделей перечисленных выше сосудистых патологий использовался программный пакет ABAQUS , схема работы которого приведена на рис. 4. Он позволяет создавать сложную геометрию сосудов без использования сторонних систем автоматизированного проектирования продуктов. Для этого сначала были созданы вспомогательные элементы: сфера и цилиндр с помощью инструментов «фигура вращения» ( revolved solid ) и «фигура выдавливания» ( extruded solid ). К полученным объектам была применена операция сложения, а затем на стыке – операция сглаживания. В результате были получены геометрические модели мешотчатой и фузиформной аневризмы, стеноза и атеросклеротической бляшки, на которые затем накладывались объемные вычислительные сетки.

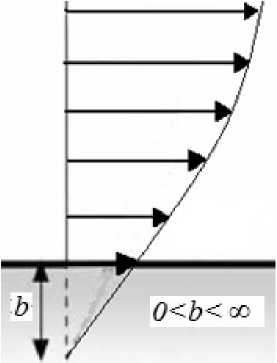
Рис. 3. Профиль скорости при режиме полупроскальзывания на стенке сосуда

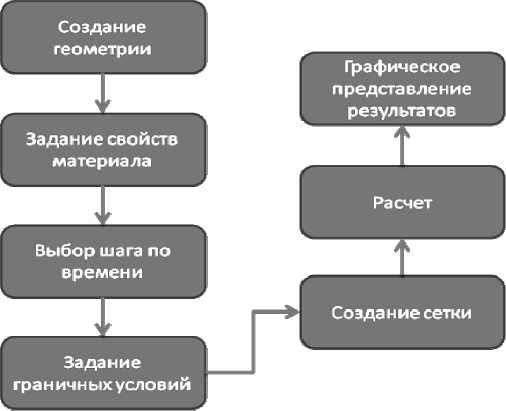
Рис. 4. Схема работы пакета ABAQUS

Результаты расчета и их анализ

Численный расчет течения крови, определяемого уравнениями (1) и (2), осуществлялся методом конечных элементов с использованием упомянутого выше пакета ABAQUS . Для этого предварительно задавались реологические с войства крови, определенные соотношением (3), начальные условия (4) и граничные условия по формулам (5)–(7).

В результате проведенных расчетов были получены распределения скорости и давления в каждом узле вычислительной сетки с шагом по времени 0,01 с в течение одного пульсового периода. Наиболее интересные результаты были получены в м о мент времени t = 0,5 с, который соответствует максимальному значению потока крови.

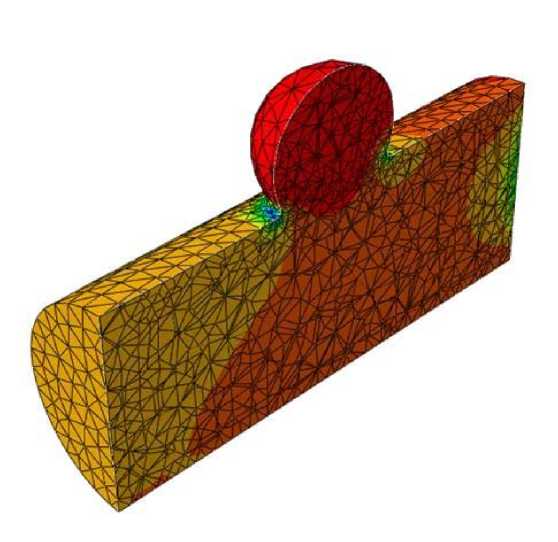
В частности, в стенозированном сосуде и н терес представляет распределение давления в потоке крови (рис. 5, a ). Перед зоной сужения оно повышается до максимального значения, падает в зоне сужения и достигает минимального значения перед расширением. После выхода из зоны сужения появляется зона незначительного повышения давления, соответствующая пульсово м у режиму, что свидетельствует об ослаблении пульсового характера потока.

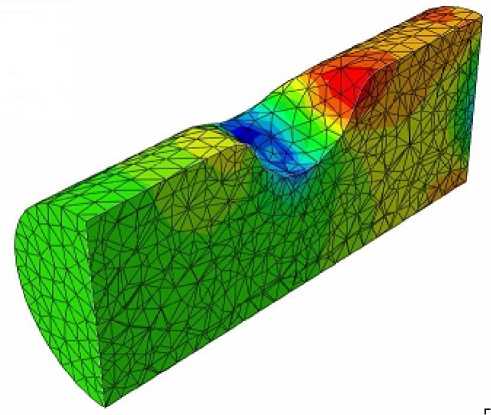
При наличии бляшки распределение давления более сложное и не с толь ожидаемое, как в зоне стеноза (рис. 5, б ). Давление возрастает в небольшой зоне потока перед бляшкой, потом падает при огибании бляшки до минимума и возрастает до средних значений после ее огибания.

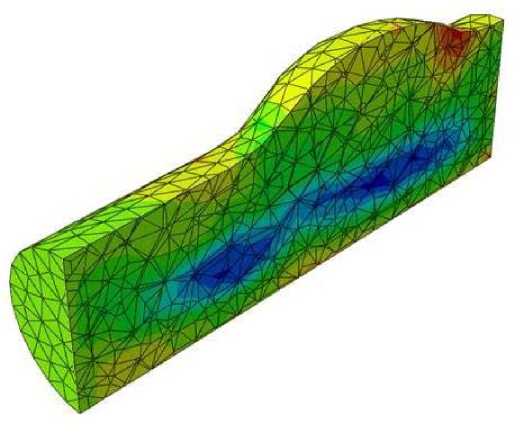
При моделировании потока в зоне фузиформной аневризмы обнаружено появление области пониженного давления под осевой линией сосуда (рис. 5 , в ). В случае мешотчатой аневризмы наблюдается вихрь, занимающий всю об л асть патологии (рис. 6). Его зарождение начинается в момент времени, равный 0,3 с, что соответствуетмоменту смены знака производной функции потока на входе в артерию. Вихрь развивается в течение 0,2 с и затем исчезает. Кроме того, в пристеночном слое возникают кратковременные обратные токи крови. Внутри самой аневризмы наблюдается повышенное давление, что само по себе вполне ожидаемо (рис. 5, г ). Однако наличие небольших зон пониженного давления до и после бляшки свидетельствует о весьма опасном перепаде давления по сравнению с остал ь ным сосудом, что в реальности может привести к прорыву его стенки.

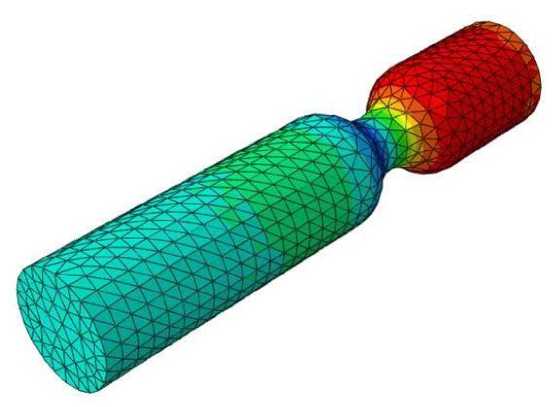
а

б

в

Рис. 5. Распределение давления в области стеноза ( а ), бляшки ( б ), мешотчатой аневризмы ( в ), фузиформной аневризмы ( д ) при t = 0,5 с

д

Рис. 5. Окончание

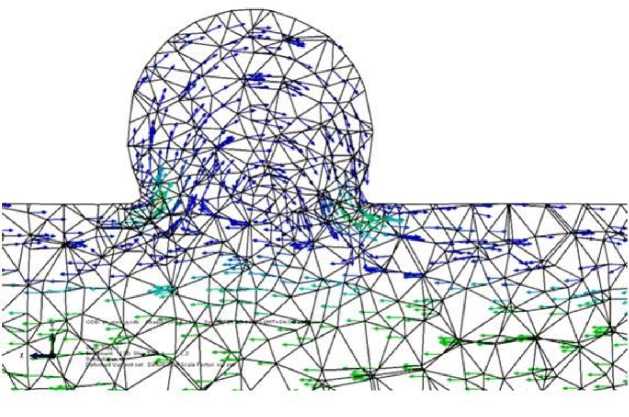
Рис. 6. Наличие вихря в зоне мешотчатой аневризмы

Заключение

Таким образом, разработанная математическая модель течения крови в окрестностях сосудистых патологий позволяет получить более адекватное представление о характере течения крови за счет учета ее неньютоновских свойств, предложенного способа задания пульсового режима и использования режима полупроскальзывания при взаимодействии крови со стенкой сосуда. Следует отметить, что в приведенных рисунках представлено только несколько частных примеров полученных результатов в отдельные моменты времени, иллюстрирующих работу предложенной модели в условиях нескольких видов сосудистой патологии. Несмотря на идеализированные формы патологий, модели дают не только качественное представление о характере течения, но и позволяют получить количественные характеристики потока. При этом они предполагают возможность изменения геометрических форм патологий, приближая их к реальным формам конкретных пациентов, полученных при их обследовании.