Компьютерное моделирование при проектировании железобетонного каркаса двухэтажного жилого дома

Анализ работы строительных конструкций показывает, что аварии возникают в результате случайного совпадения нескольких факторов [1]: отклонения нагрузки в худшую сторону; снижения механических свойств материала; неблагоприятных условий эксплуатации; неточности расчетной схемы и т.д. При расчете по несущей способности условие прочности выражается в общем виде неравенством [2]:

Ттах(^П, У/, Уп) — Tu m{Tl(S, Нп,ут,Ус), где Tma%- внешнее расчетное усилие; Tu^m.in- сумма внутренних предельных усилий (М, Q, N).

Неравенство (1) показывает, что значения М , Q , N в сечении элемента конструкции от внешних нагрузок при самых неблагоприятных условиях не должны превышать его теоретическую минимальную несущую способность. Если неравенство не соблюдается, то прочность конструкции не обеспечена.

В связи с проектированием двухэтажного жилого дома возникла задача исследования НДС железобетонной рамы этого дома со схемой нагрузок на поперечную раму (рис. 1 а) в САПР Mathcad [3, 4]. Расчет каркаса здания сводится к определению усилий в рамной системе [3], стойками которой являются колонны, ригелями балки из сталефибробетона с расчетными характеристиками: Rtr : = 4.5 • МПа - расчетное сопротивление на растяжение; Rcr := 22.5 МПа - расчетное сопротивление на сжатие; Er : = 31 • 103 • МПа - модуль упругости.

Материал колонны - железобетон с расчетными характеристиками: Rbk : = 11.5 • МПа - расчетное сопротивление бетона колонны на сжатие; Ek : = 31 • 103 • МПа - модуль упругости бе-кН тона колонны; qn.кол := 180 — - нормативная постоянная распределенная нагрузка ко лонны; /у := 1.2 - коэффициент надежности; q := q1Lкол • у;- - расчетная нагрузка колонны.

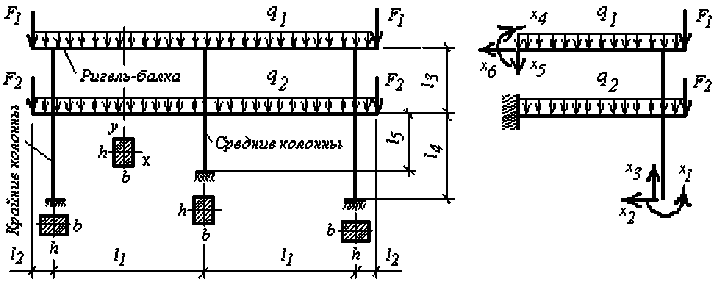
Рисунок 1 – а - расчетная схема рамы двухэтажного жилого дома; б - эквивалентная система

В сборе нагрузок на верхний ригель учтены временная нагрузка в холодном чердаке, собственный вес скатной кровли и снеговые нагрузки. Расчетные нагрузки: на покрытие 9.5 кН, из них временная нагрузка 2,4- кН. На перекрытие 10^ кН, из них временная нагрузка 2- кН. Се чение колонн b X h. Колонны ориентированы в плоскости рамы: крайние - стороной h, средние – стороной b. Рамная конструкция каркаса здания рассчитывается на действие вертикаль- ных и горизонтальных усилий методом заменяющих рам в двух взаимно перпендикулярных направлениях [1] (здесь приводится расчет на вертикальную нагрузку). Расчетная схема каркаса здания представлена (рис. 1 а) в виде 12 раза статически неопределимой рамы (Z1 := 6 м; Z2 := 0,4 м; Z3 := 3 м; Z4 := 3,8 м; Z5 := 2,9 м). Используя свойство симметрии, снижаем число канонических уравнений до 6. Канонические уравнения (3) метода сил приведены ниже и выражают равенство нулю перемещений точек приложения сил Х1, ^,х6 в направлениях отброшенных связей.

В программе при вычислении Мf(s) и Mj(s) использована «путевая координата» s, кото- рая непрерывно увеличивается по мере перемещения текущего сечения от начала отсчета и до конца рамы [4]:

М 1

I-1 if L2 < s < L3 1-1 if L3

Программные модули М , (s)

М 2

(s) := |

¹ • ^(L3

1 • Z4

— s) if L2 < s < L3 if L3 < s < L4

1⁰ if L 3 4

" ³ (^SH -1._a<- _s )

I 1 • s                  if 0 < s i

M₅(s) :=|1-Z 1               if L i 2

|—1 • l i + 1 • (L 4 — s) if L 3 < s < L 4

I —1 if 0 < s < l i M 4 (s):= —1 if L i 2

11    if L₃< s < L₄

I1-(s —L i ) if L i 2

^M 6 ^(s): | — 1^l₃      if L₃< s < L₄

M_f(s) : =

Q i •s²

Q i • ^l 2

Q i • l i

+ F_i • (L

i

^Q 2 • ^(L 4

Q i • l 2

—

s')2

Q i • l²

^q 2 • ^(L 5

—

Программный модуль Мf(s)

—

—

s)

F i • l i

^{+ Q} 2 • ^l 2 • ^(l 4

^{+ Q} i ^ ^l 2 • ^(l 4

s)2

+ F 2 • (l₅

—

+

—

s) + F i • (L 4 + l i

—

s')

+li

s)

—

s) + F i • (L 4 + l i

—

s)

if 0 < s < li if li < s < Li if Li < s < L2

if L 3 4

if L₄5

Коэффициенты 5ц,..., 855 и свободные члены 8j f ,..., 86 f канонических уравнений вычислили при помощи интеграла Мора [3, 4], приводим только отрывок, при этом учтено, что ^ t] — S jt (по теореме о взаимности перемещений):

5ц := ^ • (f^ ³ M^ds + f² MKs)ds) ;

5 if :=Aff⁴M i (s)^M f (s)ds;

J       E*IX 2b3                J

(s') ds + J  M₆ ² (s)ds) .

5 if := ^-^ f^ M i (s) lM f (s)ds;

⁵ 6f:=^-; (f 2 M 6 (s) • M f (s)ds + J l2; M 6 (s) • M f (s)d^)

Канонические уравнения решаем в вычислительном блоке Given-Find :

Given   5_ii • X i. + 5_i2 • x₂ + 5 i3 • X 3 + 5 i4 • X 4 + S ig • X 5 + 5 i6 • X 6 + 5 if — 0

5 6i • X i + 5 6i • X i + 5 63

Find(xi,x2,x3,x4,xs,x6) —

• •    ^x 3 ^{+ S} 64 • ^X 4 ^{+ S} 65 - 1.618 x 10⁴/ "  1.278 x 10⁴N 3.525 x 10 5 N —1.522 x 105}  ;

• — 1.436 x 10 5 N

• -    —5.48 x 10⁴N -

• ^X 5 ^{+ 5} 66 • ^X 6 ^{+ 5} 6f = ⁰

^Xil x₂ X₃

X 4

Xg

-X6-

" 1.618 x 10⁴J "  1.278 x 10⁴N ^3.525 x ¹⁰ 5 ^N —1.⁵²² x ¹⁰⁵ — 1.436 x 10⁵N ^- —5.48 x 10⁴N ^-

Определив неизвестные силовые факторы (5), составляем программный модуль для суммарных изгибающих моментов M_tot (s) и строим выпрямленную эпюру (рис. 2):

Программный модуль Mtot (s) M_tot(s)

• — Х4 + "у- + Х5 • s

HH^ip^ + Fi • (Li — s)

• -    Х4 + Х5 • 11 + Х6 • (s—Li) + ^у1 - 91-2 - fl • l2

• ^{- Х}1 + % 2 • ^(L3 ^{— s)}

• ^{9 2} ( 4 ^S ) ⁺ 4 2 • ^l 2 • ( ^L4 ⁺ ~ ^{— s) + F}2 • ^(L4 ^{+ l} 2 ^{— s) —}

• ^— ^1 ^{+ 4}1 ^ ^l1 ^ ^(L4 — ^s) + ⁴1 ^ ^l2 ^ ( ^L4 ⁺ ^ — ^s) ₊

^+F1 • ^(L4 + ^l2 ^{— s) —} Х д • ^li + Х д • ^(-4 ^{— s) —}

• —%6 • I3 — %1 + %2 • I4 — Х3 • (—4 — S) + %4

— + F^. — s)

if 0 < s < 1 1

if 1 1 < s < L 1

if — i < s < — 2

if L2 < s < L3

if L₃< s < L 4

if L 4 g

Как видно из рисунка 2, выпрямленная суммарная эпюра M_tot (s) построена правильно.

После этой проверки она на рисунке 3, а представлена в привычном виде. Проверим прочность ригеля как балки с исходными размерами по нормальным напряжениям. Предварительно

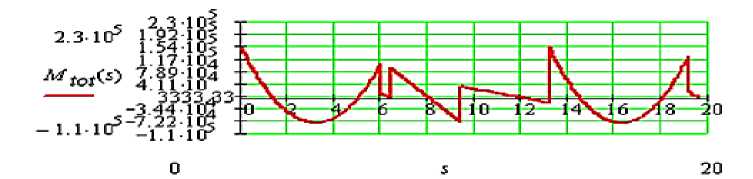
Рисунок 2 – Выпрямленная суммарная эпюра изгибающих моментов M_tot (s)

определяем момент сопротивления сечения И^.г := ^, W^.r = 5.333 • 10 3м3. Наибольший из- гибающий момент по абсолютному значению Мтах := 154 • кН• м. Из условия прочности l^tl = °тах, l°tl = Мтах < Rtг, находим отах = ^^2^ = 28.875МПа. Перенапряжение состав-тах   с     WXr                      .. И/хг ляет gmax Rtr • 100 • % = 541.667 • %. Это слишком большая перегрузка. Увеличив размеры Rtr сечения ригеля до 6Г := 0.4 • м , йг := 0.7 • м , получаем тах = 4.714МПа , т.е. отах Ихг

:= 4.714 МПа . Перенапряжение оставляет £ ™“^х_ ?^ ^ ^г • 100 • % = 4.756% , т.е. 4.756% < 5%. ^{1       1}                                 Rtr

Таким образом, прочность ригеля обеспечена при данном увеличенном размере сечения ригеля.

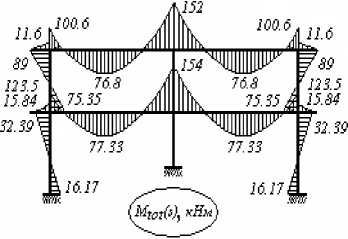
а

Рисунок 3 – a - cуммарная эпюра изгибающих моментов M_tot (s); б - деформированное состояние

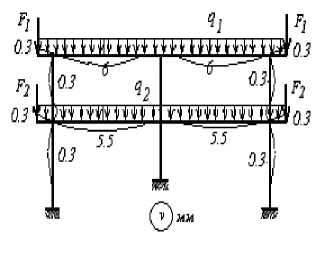
б

рамы в привычном виде

Проведем проверку жесткости рамы с заданной нагрузкой. Форму изогнутой оси рамы определяем численным интегрированием дифференциального уравнения изогнутой оси рамы при помощи встроенной функции Odesolve , которая использует метод Рунге-Кутта 4-го порядка с фиксированным шагом интегрирования. Сначала составляем программные блоки для вычисления /(s') и E(s) по участкам рамы:

	! х	Программные модули /(s) и E(s)			— s — L1
		if 0 — s — L 1	Er	if 0
/(S) : =	! х	if L 1 — S — L 3       E(s):=	Ek	if L i	— s — L3
	1 х	if L3 — s — L5	Er	if L3	— s —L 5

После этого дифференциальное уравнение изогнутой оси рамы решаем при помощи вычислительного блока Given Odesolve :     Given  ^—vtis) = — ^{M tot (s}^ . Начальные условия:

ds²             E(s>I(s)

v(0) = 0,   v(9.4) = 0 , ответ v : = Odesolve(s, 19.6,1000) .

Результаты машинного решения дифференциального уравнения изогнутой оси рамы представлена на выпрямленной оси рамы на рисунке 4 a. Деформированное состояние рамы в привычном виде показана на рисунке 3 б. Допускаемое значение прогиба ригеля f : = — • 1г,

“    600

fv := 10 • мм. Как видно из эпюры рисунка 4 а, максимальное значение прогиба ригеля не пре- вышает 6 мм, следовательно, жесткость ригеля обеспечена.

Определяем вертикальные нагрузки на колонны: qбетона = 2.4 • Т; qж.бетона = 2.5 • Т; qпог.жб := 25 • кН• 0.4 • м • 0.2 • м; qпог.жб = 2 • кН. Вертикальные нагрузки на верхние сечения крайних колонн определяем из уравнения равновесия верхнего ригеля (рис. 4 б): £Ма = 0.

Начальное значение Rm«m := 10 • кН; Given —х - £101+22—f • (l + l ) + r    •l = кр. вер                      4      2       112     кр. вер  1

0; Find(Rкр.вер) = 182.917 • кН.

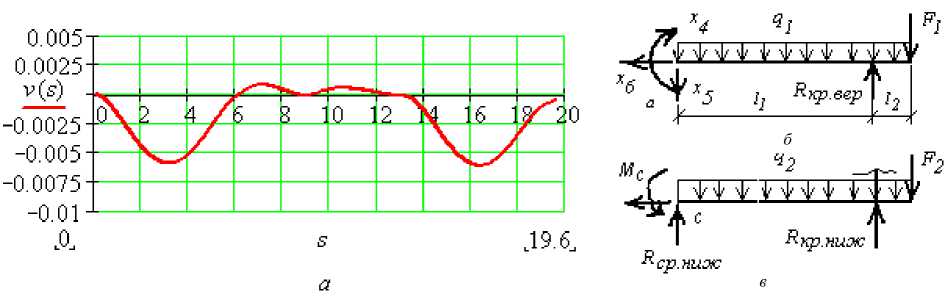
Рисунок 4 – a - выпрямленная (машинная) эпюра изогнутой оси рамы; б - расчетная схема верхнего ригеля; в - расчетная схема нижнего ригеля

Вертикальные нагрузки на нижние сечения крайних колонн определяем из уравнения равновесия нижнего ригеля (рис. 4 в) :   £М с = 0R _кр . _ниж := 30 • кН М_с := 205.31 • кН • м

Given Мс — ^ — q2 • l2 • (li + |) — F2 • li + Rкрниж • li = 0; Find(Rкр.ни) = 203.755 • кН.

—

^кр (^кр ) :

R кр. вер

—

Программный модуль ^ _кр (рис. 4 а)

R кр. ниж

—

^q пог . жб • ^(l3 ^{+ l}4    ^ кр ) ^{if 0 —} ^ кр — ^l4

-R кр. вер

—

^q пог . жб

• ^(l3 ^{+ l}4

^кр )

if l4 — Zкр — l4 + 1з

Вертикальную нагрузку на нижнее сечение средней колонны определяем из уравнения

равновесия нижнего ригеля: R_c р . _ниж := 10 • кН

Given ^12 - ^^ -F2-L- Кспниж • ^ = 0   Find(RCDHUVC) = 2 • 177.167 • кН

2         2         2   2      Ср . НИ-^Ж   1                       Ср . НиЖ

Программный модуль для N_c р (рис. 4 а)

N ep (z) : =

^R cр . вер    ^R cр . ниж   Q пог . жб "  ^(l3 + ^l5 ^{z)     if 0 — z — l}5

^R cр . вер   У пог . жб "  ^(l3 + ^l5   ^{z)                        if l} 5 — ^z — ^l 5 + ^l 3

z:= 0,0.01..5.9

z_ср := 0,0.01. .6,8

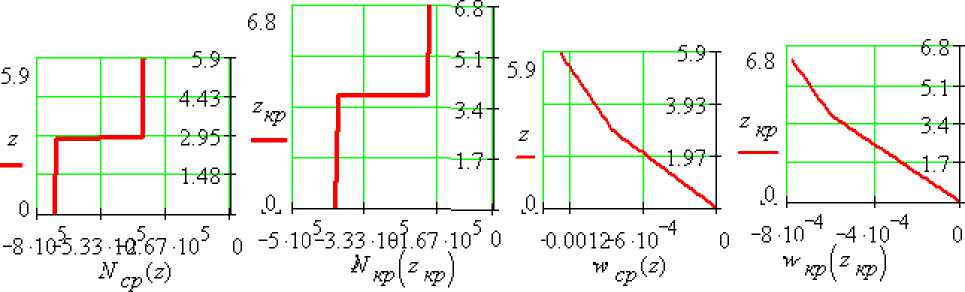
Рисунок 5 - Эпюры нормальных сил N _сp (z), N _кp (z _кр ) осевых перемещений сечений и ^р и м кр по длине средней и крайних колонн

Проверка прочности колонн. Условие прочности бетонной колонны (средняя колонна наиболее нагружена, ее и рассматриваем) omax := W™a* — Rb "Уь, где Nmax : = 729.09 • кН -максимальное значение нормальной силы в колонне; уь : = 0.9 - коэффициент условий работы бетона; расчетное сопротивление бетона В20 осевому сжатию Rb : = 11.5 • МПа, откуда находим: <7max := w™“z, cmax = 9.114 • 106 • Ра, Rb -уь = 10.35 • МПа. Как видно, прочность ко- лонн достаточная. Величину осевого перемещения сечения w(z) по длине колонны определяем, интегрируя дифференциальное уравнение растяжения-сжатия колонны (эпюры осевых перемещений сечений представлены на рисунке 5):

i4(z) := | ^{0 if 0 — Z — l}3 + ^l5 . Given —w(z)= " ^{ср (}^ . Начальные условия w(0) = 0, Ь • a                           d ^z         -E fc -^(z)

\^ср := Odesolve(z, 5.9,1000). Given ~^кр(zкр)=^кр"^кр). Начальные условия \^кр(0) = 0, wK$) := OdesoZne(zкр,6.8,1000) : z := 0,0.01..5,9; zкр := 0,0.01. .6,8. Условие жесткости колонны при расчете по 2-й группе предельных состояний w ≥ wu, где w=1,5 мм – искомое перемещение; wu = 1,5 • мм - предельное значение перемещения, выполняется.

Таким образом, проведенное исследование НДС каркаса рамной конструкции двухэтажного жилого дома показало, что запроектированное здание отвечает всем требованиям СНиПа. Следует отметить, что использование математического пакета Mathcad при расчете стержневых строительных конструкций [1, 4] вполне оправдано тем, что система достаточно просто реализует вычислительный алгоритм любой сложности. Традиционное программирование, как известно, делит процесс решения задачи на три независимых этапа: написание программы, отлаживание и оптимизацию. В среде Mathcad эти процессы слиты воедино, т.е. создание программы идет параллельно с ее отладкой.