Компьютерное моделирование процесса переноса тепла в неоднородных средах с использованием технологий параллельных вычислений
Автор: Прохоров С.А., Тен А.В.
Журнал: Математическая физика и компьютерное моделирование @mpcm-jvolsu
Рубрика: Моделирование, информатика и управление
Статья в выпуске: 3 т.26, 2023 года.
Бесплатный доступ
В данной работе изучено двумерное линейное уравнение теплопроводности с дробным порядком дифференцирования и составлен вычислительный алгоритм его численного решения. Дробные производные по пространству и времени представлялись при помощи определения Римана - Лиувилля, а для их аппроксимации использовалось определение Грюнвальда - Летникова со сдвигом. На основе вычислительного алгоритма написана программа для компьютерного моделирования процесса теплообмена в неоднородных средах. Разработана версия программы с использованием технологии параллельных вычислений OpenMP. Компьютерная модель протестирована рядом численных экспериментов по решению задачи распространения теплового импульса. По результатам моделирования было изучено влияние дробного порядка дифференцирования на процесс теплопроводности.
Компьютерное моделирование, разностные схемы, дробное дифференцирование, уравнение теплопроводности, параллельные вычисления
Короткий адрес: https://sciup.org/149144545
IDR: 149144545 | УДК: 536.2 | DOI: 10.15688/mpcm.jvolsu.2023.3.3
Текст научной статьи Компьютерное моделирование процесса переноса тепла в неоднородных средах с использованием технологий параллельных вычислений
DOI:
Значительная часть процессов в природе происходит в пористых средах и не может быть описана при помощи уравнений, относящихся к теории механики сплошной среды. Для учета особенностей неоднородности среды при моделировании данных процессов можно использовать математический аппарат дробного дифференцирования, позволяющий учитывать фрактальность среды [3].
Идея о распространении интегрирования и дифференцирования на дробные порядки существует с самого зарождения интегрального и дифференциального исчисления. Разработано множество способов для определения производной дробного порядка, одними из популярных являются определения Римана — Лиувилля [4; 8], Капуто [7] и Грюнвальда — Летникова [12].
Хотя основы дробно-дифференциального исчисления были заложены еще в позапрошлом веке, их широкое применение началось только в последние десятилетия. В следующих задачах использование математического аппарата с дробными производными оказалось особенно эффективным: классическая механика (обратные задачи) и гидродинамика (движение тела в вязкой жидкости) [9], конвекция-диффузия (решение начально-краевых задач с дробной производной Капуто) [7], теплопроводность (теплообмен в пористых средах, распространение тепла в аэрогелях) [1], динамика турбулентной среды, теория фазовых переходов, пространственные и временные корреляции в жидкостях, просачивание в пористых средах, вязкоупругость (реология полимеров) [2], решение начально-краевых задач для уравнения конвекции-диффузии.
Дробное дифференцирование является актуальной областью исследования, так как дает более реалистичные результаты, чем классические уравнения механики сплошной среды. Дробное исчисление может быть распространено на различные области физических и естественных наук. Кроме того, дробные операторы имеют больше степеней свободы, и они обобщают целочисленные дифференциальные операторы [11]. Некоторые линейные и нелинейные динамические задачи дробного порядка решаются с помощью полуаналитических решений с использованием преобразования дробной суммы [13; 14].
Основным преимуществом дробного дифференцирования перед целочисленным является возможность учитывать микро- или наноструктуру моделируемого объекта, но за это приходится расплачиваться более высокой вычислительной сложностью алгоритмов их численного решения.
1. Уравнение теплопроводности в неоднородных средах
При рассмотрении неоднородной (фрактальной) среды возникает дробная производная по координате (пространству), значение которой определяется посредством размерности фрактала. В случае прилипания атомов вещества к порам среды, в которой происходит теплообмен, необходимо учитывать нелокальность по времени при помощи дробной производной по времени. Также стоит сказать, что при в = 2 уравнение (1) превращается в классическое уравнение теплопроводности, а при в = 1 получаем уравнение переноса примеси [6].
Ниже записано одномерное уравнение теплопроводности в консервативной форме с дробным порядком дифференцирования по времени и пространству:
д а Т _ д в Т dt a дх в ’
где Т (x,t) — распределение температуры; К = const — коэффициент теплопроводности; 0 < а < 1 — дробный порядок дифференцирования по времени; 1 < в < 2 — дробный порядок дифференцирования по пространству.
Уравнение (1) может быть расширено на двумерный случай. Двумерное уравнение с дробными производными по пространству и времени имеет следующий вид [1]:
д а Т _ д в Т , _ д в Т
dt» Кх дxв + Ку дув + /(t,x,у), где Т(x,y,t) — распределение температуры; КЖ,КУ — коэффициенты теплопроводности по x и у координате соответственно; /(t,x, у) — функция, задающая источники тепла.
2. Численное решение двумерного уравнения теплопроводности в неоднородной среде
Решать будем уравнение теплопроводности вида (2), которое является классическим представителем уравнений в частных производных параболического типа. Перепишем уравнение в отсутствии внешних источников тепла и добавим в уравнение учет таких теплофизических характеристик, как плотность р и теплоемкость с:
D^ =
^^Т + К ^ D в T.
рс ж рс у '
где D » — параметр, отвечающий за дробный порядок дифференцирования по времени а (0 < а < 1); De — параметр, отвечающий за дробный порядок дифференцирования по координате x (1 < в < 2); D ^ — параметр, отвечающий за дробный порядок дифференцирования по координате у (1 < в < 2); р и с — плотность и теплоемкость вещества.
Для аппроксимации дробных производных по пространству использовалось определение Грюнвальда — Летникова со смещением. Выражения для расчета D ^ , D ^ имеют
Для аппроксимации дробной производной по времени применялся достаточный признак существования дробной производной Римана — Лиувилля, в области [t ^ , ^+1 ] при 0 < а < 1. Согласно нему D » равно:
DаT (М,у)к
1 I Т(t k ,x,y) Г(1 — а) I (t k+i — tк) а
t k + / t k +1
Т ‘ (x, s^ds (tk +1 — s ) »
Производную Т ‘ (т, x, у) в области [t k , t ^ +1 ] можно представить с помощью конечной разности:
(S
Т(t k+1 ,x,y) - Т(t k ,х,у^
τ
В итоге получим следующее равенство для аппроксимации дробной производной по времени:
D т(t,x,y')\tk « Г(1 — а) х х / Т(tk,х,у) + Т(tk+i,x,y) - Т(tk,х,у) Гtk ds \ =
Х \ (t k +i - Na т Л+1 ( t k +i - s ) a)
= Т - аТ п Г(1 - а)(1 - а)та
Используя выражения (3–5) и уравнение (3), получим следующую явную разностную схему:
Если известно распределение u^ j на п-м временном слое, то значение и п +1 в каждом г, i -м узле вычисляется из соотношения (9) по формуле:
пп+1 - Kx(Г(2 а)т ) (ип впп + ^ ш,ип+
Ui,3 = -вл M«+1,t - eUi,3 + Z^^kUi-k+1,3
hxРС \ k=2/
K y (Г( 2 - а ) т а ) / п 6 п , у1 п ^ , п
+ Гр I U i,j+1 - e U i,j + У ^ k U ij - k+1 + a u i,j .
hyРС k=2/
Для устойчивости схемы (9) необходимо выполнение следующего условия [5]:
та /Kx Kx\а pc \ hX hX ) (2 + в)Г(2 - а)
3. Применение технологии OpenMP для разработки параллельной версии программы
Тема увеличения эффективности вычислений весьма актуальна для задач, которые связаны с большими объемами вычислительных работ. Некоторые задачи требуют нескольких месяцев расчетов. Однако с развитием технологий и программного обеспечения стало возможным создавать программы с эффективным быстродействием.
На основе разностной схемы, приведенной выше, запишем вычислительный алго- ритм для решения двумерного уравнения теплопроводности в неоднородных средах:
дТ
Этап 1: Задание начальных условий: Т(х,у, 0) и dt Ш
Этап 2: Вычисление шага по времени τ из условия устойчивости для конечноразностной численной схемы (11).
Этап 3: Формирование значений температуры Т(x,y,t) на границах расчетной сетки (задаются граничные условия). В данной программе возможно задание граничных условий I, II и III типа.
Этап 4: Расчет значений .0 е, ))У согласно выражениям (4-5) для всех ячеек T ^n (j = 1,..., М ; г = 1,..., N ) на текущем временном слое t k .
Этап 5: Определение распределения тепла Т + согласно (9) на следующем временном слое t ^ +i .
На следующем временном интервале расчеты повторяются со второго этапа по пятый, до тех пор, пока не будет достигнуто время окончания расчетов. Вычислительная сложность данного алгоритма составляет О(п 3 ).
На основе описанного выше алгоритма разработана программа на языке С++, с помощью которой проведены серии численных экспериментов с разными значениями дробного порядка дифференцирования.
В данной работе для распараллеливания программы применялся стандарт OpenMP, который представляет собой расширение исходного языка программирования. OpenMP предоставляет простой способ использовать для вычислений ресурсы нескольких вычислителей, без необходимости использования специфичного API операционной системы.
Для численного решения уравнения теплопроводности производится замена частных производных в дифференциальных уравнениях их разностными аналогами, то есть применяется явная конечно-разностная схема. Следовательно, область расчетов [0 ... N]х х [0... М] разбивается на ячейки с постоянным шагом по времени и пространству. Для распараллеливания программы расчетная область делится на равные подобласти согласно количеству потоков в выполняемой параллельной программе. На каждом полученном таким способом интервале процесс интегрирования осуществляется отдельным потоком, при этом в связи с использованием явной схемы соседние процессы должны обмениваться крайними значениями, полученными на предыдущем шаге, для выполнения следующего шага. В OpenMP описанное разделение на подобласти осуществляется при помощи условия schedule с типом static, который равномерно распределяет итерации между потоками.
Данным способом были распараллелены циклы для этапов 3–5. Разделяемыми переменными в данных циклах являются массивы, содержащие распределение температуры на текущем и следующем временных слоях, остальные переменные записаны под условием private , то есть каждый поток имеет свои копии данный переменных [10].
Для оценки эффективности параллельных вычислений рассчитаны следующие показатели параллельного алгоритма: ускорение (S p ) и эффективность (Е р ) представленные ниже в таблице. Отладка и тестирование программы проводились на ПК (персональном компьютере) со следующими характеристиками: процессор — Intel(R) Core(TM) i5-8250U c 4 ядрами и 8 потоками, частотой 3,60 GHz; оперативная память 8 Гб; графический процессор — NVIDIA Geforce GTX 1060 c оперативной памятью 6 Гб.
Время работы Т р , ускорение S p и эффективность распараллеливания Е р вычислений c помощью OpenMP
|
Z \ t ( c ) |
Т |
Т 2 |
Т 4 |
Т 8 |
S 2 |
S 4 |
S 8 |
Е 2 |
Е 4 |
Е 8 |
|
10 2 |
0 , 038 |
0 , 039 |
0 , 042 |
0 , 045 |
0 , 95 |
0 , 88 |
0 , 84 |
0 , 47 |
0 , 22 |
0 , 11 |
|
10 3 |
0 , 863 |
0 , 559 |
0 , 394 |
0 , 256 |
1 , 54 |
2 , 19 |
3 , 37 |
0 , 77 |
0 , 55 |
0 , 42 |
|
10 4 |
384 , 9 |
252 , 6 |
161 , 8 |
103 , 7 |
1 , 52 |
2 , 38 |
3 , 71 |
0 , 76 |
0 , 59 |
0 , 46 |
Как ожидалось, наибольшее ускорение получено при использовании восьми потоков, Z = 10 4 и равно S 8 = 3,71. Также наблюдается следующая закономерность: в случае малых значений вычислительной сложности (Z) параллельная программа работает медленнее последовательной. Это обусловлено тем, что время, затраченное на инициализацию потоков в параллельной версии программы, превышает время работы последовательной версии.
4. Результаты компьютерного моделирования процесса теплопроводности в неоднородных средах
Проведены серии численных экспериментов с разными значениями дробного порядка дифференцирования по времени α, также для сравнения проводились расчеты для классического уравнения теплопроводности.
Задача о распространении импульса решается в области [0, 2п] х [0, 2п] (N x = М у = = 50) при следующих начальных и граничных условиях:
дТ
Т(х,у, 0) = 5(х - п), — = 0, в = 2,К Х = К у = р = с = 1,
Т (х, 0, t) = Т (0, у, t) = Т (х, М, t) = Т (N, у, t) = 0. (13)
Ниже показаны результаты численного эксперимента при а = 0,2 (см. рис. 1) и а = 0,8 (см. рис. 2), вертикальная ось и показывает температуру. По графикам видно, что при более высоком значении α процесс теплообмена протекает быстрее. На рисунке 1 можно наблюдать эффект «памяти», когда начальное состояние дольше сохраняется с течением времени, а на рисунке 2 данный эффект не такой заметный, но наблюдается смещение центра столба влево.
Также проведены численные эксперименты при разных значениях дробной производной по пространству, в случае в = 1,1 (см. рис. 3) и в = 1,9 (см. рис. 4), порядок производной по времени в обоих случаях равен а = 1. В случае дробного порядка дифференцирования по пространству наблюдается перенос тепла влево. В ходе численных экспериментов также замечено, что при уменьшении значений β перенос тепла влево увеличивается.
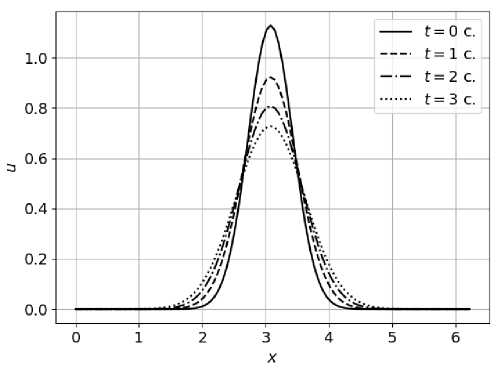
Рис. 1. График зависимости температуры Т ( ж, п ) при а = 0 , 2 за t = 0 ; 1 ; 2 ; 3 секунды
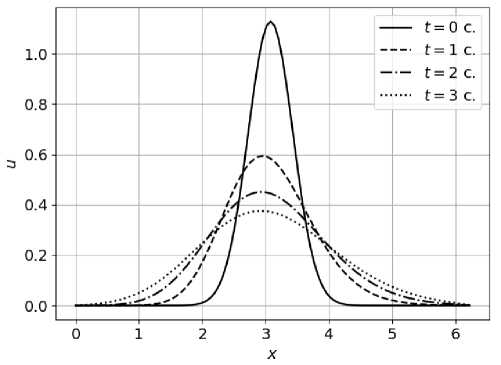
Рис. 2. График зависимости температуры Т ( ж, п ) при а = 0 , 8 за t = 0 ; 1 ; 2 ; 3 секунды
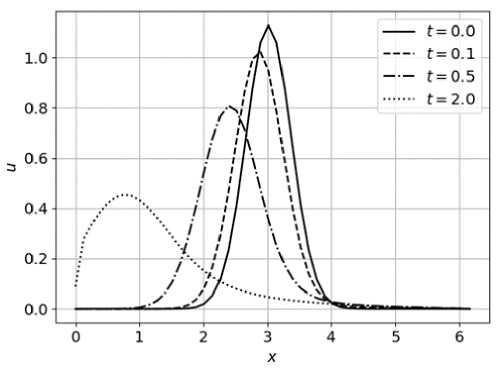
Рис. 3. График зависимости температуры Т ( ж, п ) при в = 1 , 1 за t = 0 ; 0 , 1 ; 0 , 5 ; 2 секунды
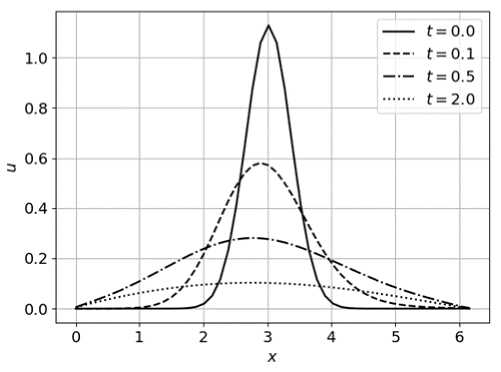
Рис. 4. График зависимости температуры Т ( ж, п ) при в = 1 , 9 за t = 0 ; 0 , 1 ; 0 , 5 ; 2 секунды
По графикам можно сделать вывод, что в случае дробной производной по времени процесс теплообмена происходит медленнее, чем в классическом случае. В случае дробной производной по пространству наблюдается процесс переноса тепла влево. Также по результатам численных экспериментов можно утверждать, что реализованная конечно-разностная схема является устойчивой и ее можно применять для решения практических задач.
Заключение
В результате работы была разработана программа, позволяющая моделировать процесс теплообмена в неоднородных средах, с последующей визуализацией полученных результатов в виде двумерных и трехмерных графиков. Подробно описаны способы определения производной дробного порядка, а также рассмотрена возможность применения линейного уравнения теплопроводности с дробным порядком дифференцирования для исследования неоднородных сред.
Для представления производных дробного порядка использовалось определение Грюнвальда — Летникова и Римана — Лиувилля, а для вычисления гамма-функции использовался метод Ланцоша. На основе данных определений проведена аппроксимация дробных производных и составлена численная схема для решения двумерного уравнения теплопроводности в неоднородных средах.
Разработана параллельная версия программы с использованием технологии параллельных вычислений OpenMP, для которой в табличном виде представлены параметры.
Проведен ряд численных экспериментов по моделированию процесса переноса тепла с различными параметрами дробного дифференцирования по времени и пространству. По результатам компьютерного моделирования были сделаны следующие выводы:
-
1. Процесс теплообмена при решении уравнения с дробным порядком дифференцирования по времени происходит медленнее, чем в классическом случае. И чем меньше значение дробного порядка, тем медленнее протекает процесс теплообмена.
-
2. При дробном порядке дифференцирования по пространству наблюдается процесс переноса. С уменьшением значения дробного порядка перенос происходит быстрее.
Список литературы Компьютерное моделирование процесса переноса тепла в неоднородных средах с использованием технологий параллельных вычислений
- Бейбалаев, В. Д. Численный метод решения начально-граничной задачи для двумерного уравнения теплопроводности с производными дробного порядка / В. Д. Бейбалаев, М. Р. Шабанова // Вестник Самарского государственного технического университета. Серия «Физико-математические науки». — 2010. — Т. 5, № 1. — C. 244-251.
- Евсеев, К. Б. Моделирование упругих свойств винтовых пружин, выполненных с применением полимерных композиционных материалов, в системах подрессоривания колесных машин с учетом реологических свойств / К. Б. Евсеев, А. Б. Карташов // Журнал автомобильных инженеров. — 2017. — № 3. — C. 17-21.
- Журавков, М. А. О некоторых направлениях применения аппарата дробного дифференцирования в механике / М. А. Журавков, Н. С. Романова // Аналитические методы анализа и дифференциальных уравнений. — 2018. — № 1. — C. 33-34.
- Карпова, А. П. Аппарат дробного интегро-дифференцирования / А. П. Карпова. — Минск: Изд-во БГУ, 2019. — 45 с.
- Корчагина, А. Н. Численное моделирование диффузионных процессов в фрактальных средах / А. Н. Корчагина, Л. А. Мержиевский // Ученые записки Забайкальского государственного университета. Серия: Физика, математика, техника, технология. — 2013. — № 3. — C. 53-59.
- Мержиевский, Л. А. Численное моделирование распространения теплового импульса во фрактальной среде / Л. А. Мержиевский, А. Н. Корчагина // Современные проблемы прикладной математики и механики: теория, эксперимент и практика. — 2011. — Т. 9, № 2. — C. 126-146.
- О численном решении начально-краевых задач для уравнения конвекции-диффузии с дробной производной Капуто и нелокальным линейным источником / А. М. Апеков, М. Х. Бештоков, З. В. Бештокова, З. В. Шомахов // Математическая физика и компьютерное моделирование. — 2020. — Т. 23, № 4. — C. 35-50. — DOI: https://doi.Org/10.15688/mpcm.jvolsu.2020.4.4
- Псху, А. В. Уравнения в частных производных дробного порядка / А. В. Псху. — М.: Наука, 2005. — 199 с.
- Учайкин, В. В. О дробно-дифференциальном уравнении Лиувилля как уравнении динамики открытой системы / В. В. Учайкин // Прикладная математика & Физика. — 2014. — Т. 37, № 25 (196). — C. 58-67.
- Chandra, R. Parallel Programming in OpenMP / R. Chandra. — San Francisco: Morgan Kaufmann Publishers, 2001. — 112 p.
- Hilfer, R. Applications of Fractional Calculus in Physics / R. Hilfer. — London: World Scientific, 2000. — 429 p.
- Machado, J. A. The Bouncing Ball and the Griinwald — Letnikov Definition of Fractional Derivative / J. A. Machado // Fractional Calculus and Applied Analysis. — 2021. — Vol. 24, № 4. — P. 1003-1014.
- Rahman, N. A. Solving Fuzzy Fractional Differential Equations Using Fuzzy Sumudu Transform / N. A. Rahman, M. Z. Ahmad // Nonlinear Sci. Appl. — 2017. — Vol. 10, № 5. — P. 2620-2632.
- Rossikhin, Y. A. Applications of Fractional Calculus to Dynamic Problems of Linear and Nonlinear Hereditary Mechanics of Solids / Y. A. Rossikhin, M. V. Shitikova // The American Society of Mechanical Engineers. — 1997. — Vol. 50, № 5. — P. 15-67.


