Компьютерное моделирование процесса распространения тепла в измерительном блоке отечественного калориметра ДСК-500

Одним из распространенных методов термического анализа является дифференциально-сканирующая калориметрия, с помощью которой можно получить информацию о теплофизических особенностях исследуемого вещества по его отклику на температурное воздействие. Запись отклика в виде экспериментальной кривой позволяет осуществить информационно-измерительное устройство – дифференциальный сканирующий калориметр (ДСК). Анализ полученной записи позволяет по известным методам определять такие физико-химические параметры вещества, как время протекания химической реакции, температура фазовых переходов, теплоемкость и т.д.

Корректность определения указанных параметров вещества по экспериментально полученным зависимостям возможно только с учетом

математической модели измерительной системы и протекающих в ней процессов. Однако, как известно, любая модель может описать реальную систему лишь в некотором приближении, что, безусловно, отражается на подлинности конечного результата.

При построении моделей процесса распространения тепла в измерительном блоке калориметра довольно часто задаются следующими допущениями:

. измерительная система абсолютно симметричная (одинаковые тигли, одинаковые датчики, одинаковое расстояние от нагревателя до ячеек с образцом и эталоном и т.п.), что позволяет избежать множества дополнительных слагаемых и коэффициентов в аналитических записях;

• .    теплообмен между ячейками с образцом и эталоном отсутствует, т.е. тепловое сопротивление материала подложки между измерительными ячейками бесконечно велико;

• .    наличие нескольких границ раздела фаз между образцом и нагревателем не учитывается, как не учитывается и пространственное разделение образца и измерительного датчика;

• .    в расчет принимается теплоемкость образца и эталона, в то время как теплоемкость конструктивных элементов измерительной ячейки не учитывается;

. во время проведения эксперимента предполагается, что тепло от нагревателей к образцу и эталону передается только за счет теплопроводности подложки, не учитывая наличие эффектов теплового излучения и конвекции газов.

Снятие каждого из этих ограничений влечет усложнение и уточнение модели, что не всегда оправдано ввиду получения незначительного прироста точности по сравнению с затратами временных ресурсов в процессе обработки данных.

Построение компьютерной модели процесса распространения тепла в измерительном блоке дифференциального сканирующего калориметра позволяет проводить численные эксперименты и их обработку автоматизировано. Это дает возможность уточнять модель, делая ее сложнее, существенно не увеличивая при этом временные затраты. Также модель, построенная сообразно реальному объекту, позволяет реализовывать задачи по его управлению и регулированию с минимальным количеством физических экспериментов, что немало важно при решении вопросов определения кинетических тепловых характеристик исследуемого образца.

В работе предлагается компьютерная модель процесса распространения тепла в измерительном блоке отечественного дифференциального сканирующего калориметра ДСК-500, особенность которого заключается в возможности управления температурой ячейки с эталоном посредством встроенного микронагревателя [1].

ИССЛЕДОВАНИЕ ПРОЦЕССА РАСПРОСТРАНЕНИЯ ТЕПЛА В ИЗМЕРИТЕЛЬНОМ БЛОКЕ ОТЕЧЕСТВЕННОГО КАЛОРИМЕТРА ДСК-500

Построение компьютерной модели базирует- ся на математическом моделировании процессов, протекающих в измерительном блоке. Кроме того требуется проведение набора экспериментов, для получения численных значений ее параметров.

В основу математической модели были по- ложены законы теплопередачи в замкнутых изобарных системах ограниченного объема [2-4].

В работе [2] авторами была получена функциональная зависимость нагрева измерительной ячейки с образцом от воздействия на ячейку с где t – время воздействия источником тепла; Kн – коэффициент передачи процесса нагрева ячейки тепловым потоком, идущим от нагревателя; Kня - коэффициент передачи нагрева ячейки; 0н -постоянная времени процесса нагрева ячейки тепловым потоком, идущим от нагревателя; 0ня - постоянная времени процесса охлаждения точечного массивного источника тепла, приложенного к ячейке с эталоном.

Численные значения коэффициентов тепловой модели измерительного блока устройства ДСК-500 выбирались исходя из того, что материалом подложки является константан с коэффициентом теплопроводности X=22 Вт/(м·К), теплоемкостью С=410 Дж/(кг·К) и плотностью р=8800 кг/м3[5]. Радиус подложки R=15 мм. Начальные условия принимались как нормальные (атмосферное давление 105 Па, температура 298 К).

Были проведены эксперименты, показавшие, что при температуре нагрева подложки свыше 410 °С расхождение с численными значениями классической модели процесса переноса тепла посредством теплопроводности составляет более чем 10%. Было предложено уравнение теплопроводности подложки в измерительном блоке отечественного дифференциального сканирующего калориметра ДСК-500 с корректирующим коэффициентом, зависящим от температуры нагрева и учитывающим влияние эффектов теплового излучения и свободной конвекции, которое дает расхождение с экспериментом менее 1% на всех температурах от 0 до 520 °С:

д T (r, t)   x Г д2 T (r, t)

д tC      р r д ² r

1 д T ( r, t )

r д

. (2)

Здесь Т – температура подложки, r – ее радиус, Х _э - теплопроводность подложки, учитывающая изменение коэффициента термического сопротивления воздуха от температуры Т . Влияние термического сопротивления воздуха при нагреве металлических объектов в реальных задачах практически никогда не учитывается, однако, если ставиться цель определить количество необходимой энергии, которая должна быть передана телу для нагрева его до определенной температуры за определенное время подобный учет необходим [6].

эталоном точечного источника тепла, которая дает численную информацию о тепловом сообще-

нии этих ячеек:

/     -£ А y (t) = 2 Kн- 1 - e 0н k 7

+

^K н ^K ня

0 ² ня

/      -1 А

1 - e ⁰ ня +

к 7

+ K н к

ня

-

0 н

ня

02 -0

ня н

/        (2 0 _ня -0 _н) t А

1 - e ^{0 ня 0 н}

СТРУКТУРНОЕ МОДЕЛИРОВАНИЕ ИЗМЕРИТЕЛЬНОГО БЛОКА ДСК-500

Используя полученное уравнение теплопроводности измерительного блока и функциональные особенности ДСК-500 [1], было составлено уравнение передаточной функции измерительного блока дифференциального сканирующего калориметра:

^W общ ⁽P) = ( W on ⁽P> ' W ,» ® ■ ^W o ⁽P) ^— — (W on (p) ■ W h . nog. (p) + W mh (P)) ■ W э (p) ^ / ( 1 + W ,c (p) ■ (W on (p) ■ W h . no,, (p) ■ W o (p)

—

—

W (P) ' W,_.(p) + Wmh (p)) ■ Wэ(p))) , где Wнп(р) – передаточная функция процесса нагрева печки, Wн.под.(р) – передаточная функция процесса нагрева подложки, Wо(р) – передаточная функция нагрева объекта, Wэ(р) – передаточная функция нагрева эталона, Wмн(р) – передаточная функция процесса нагрева микронагревателя, Wос(р) – передаточная функция обратной связи.

Структурная схема измерительного блока ДСК-500 с учетом его физических и геометрических особенностей, а также на основании законов структурного преобразования, примет вид, представленный на рис. 1.

В схеме PID1 и PID2 – ПИД-регуляторы основного нагревателя печки и микронагревателя соответственно. Регуляторы необходимы для высокоточного поддержания температуры исследуемого образца и эффективного функционирования измерительной системы.

Данная схема легла в основу компьютерной модели процесса распространения тепла от нагревателей к измерительным ячейкам посредством теплопроводности.

КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ ИЗМЕРИТЕЛЬНОГО БЛОКА ПЕЧКИ ДСК-500

В связи с выше изложенным, в работе проведено численное моделирование процессов переноса тепла в печке ДСК-500. Моделирование проводилось с использованием программ- ного продукта MATLAB и графической среды имитационного моделирования Simulink, позволяющих при помощи блок-диаграмм в виде направленных графов строить динамические модели. Вид полученной модели представлен на рис. 2.

Численные значения коэффициентов в модели рассчитывались на основании проделанного в работе эксперимента и анализа справочных данных. Стоит отметить, что модели исследуемого вещества и эталона выбрались одинаковыми для определения процесса переноса тепла в самой измерительной ячейке в независимости от исследуемых веществ. Также вторичные преобразователи, усиливающие сигнал с первичных преобразователей (термодатчиков), были выбраны с единичным коэффициентом усиления, поскольку они могут быть настроены одновременно с настройками регуляторов и на сам процесс распространения тепла не влияют.

Результатом моделирования стал график, отражающий зависимости становления дифференциальной температуры при подаче на вход модели ступенчатого воздействия в виде сигма-функции (рис. 3).

Колебательный вид графика становления дифференциальной температуры, представленного на рис. 3, объясняется многоконтурностью системы, а также довольно высокой степенью характеристического уравнения передаточной функции всей системы.

Функциями регуляторов являются как раз уменьшение амплитуды колебаний и увеличение быстродействия системы, позволяющей за меньшее время выводить дифференциальную температуру на заданный уровень.

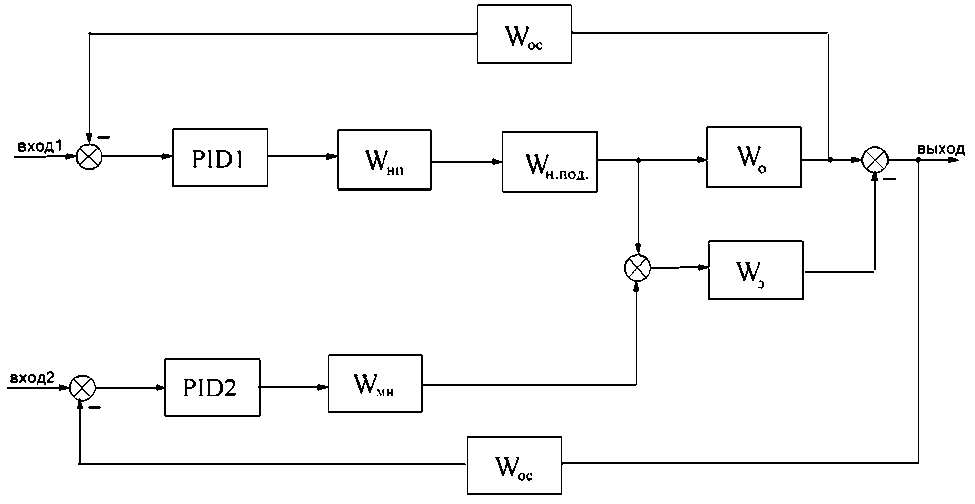
Рис. 1. Структурная схема измерительного блока ДСК-500

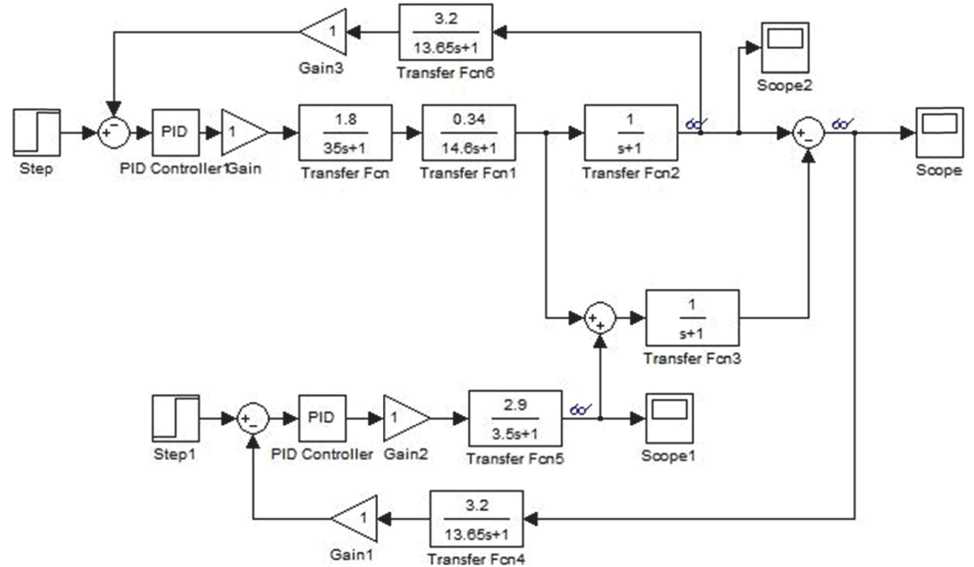
Рис. 2. Компьютерная модель измерительного блока ДСК-500

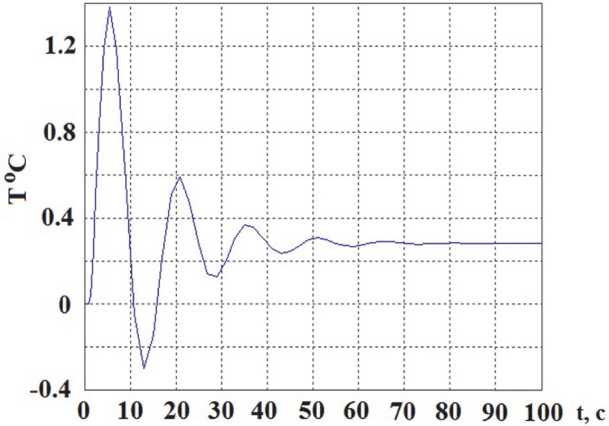
Рис. 3. График становления дифференциальной температуры

ЗАКЛЮЧЕНИЕ