Компьютерное моделирование процессов фотовозбуждения донорно-акцепторных комплексов

Сверхкороткие лазерные импульсы длительностью 10 - 13 ^ 10 - 14 c используются для исследования кинетики фотохимических реакций в донорно-акцепторных комплексах (ДАК), выступая при этом и как инструмент оптической накачки реагентов, и как средство детектирования текущего состояния молекулярной системы. Методы фемтосекундной спектроскопии позволяют фиксировать структуру коротко-живущих реакционных интермедиатов, то есть фактически исследовать микроскопические механизмы химических превращений [1; 8]. Вместе с тем интерпретация экспериментальных данных предполагает, как минимум, наличие достаточно точной и подробной математической модели исследуемых процессов, а также методов исследования модельных уравнений (аналитических или численных) и извлечения из них количественной информации для анализа экспериментальных данных. Основой для описания сверхбыстрого переноса электрона между донорным и акцепторным компонентами молекулярной системы в многомодовом полярном растворителе может служить стохастическая модель фотохимической реакции (см., например, [4]). Модель использует разработанные ранее в [7; 9] понятия дебаевской поляризационной моды растворителя, параболического диабатического терма, резонансного электронного перехода в точке пересечения термов, соответствующих состояниям системы с различной локализацией электрона в пространстве, а также учитывает диффузионный характер движения частиц вдоль координат растворителя. С математической точки зрения модель представляет собой систему дифференциальных уравнений в частных производных, описывающих эволюцию плотностей распределения частиц в пространстве, заданном отдельными модами растворителя. В большинстве приложений конфигурационное пространство задачи ограничено 1–3 поляризационными модами, в то время как число уравнений модели может достигать нескольких тысяч.

Большинство исследований, использующих стохастическую модель для описания сверхбыстрых фотоиндуцированных реакций в ДАК, рассматривают заселение возбужденного состояния молекулярной системы как мгновенный процесс. Это предположение нельзя считать корректным в ситуациях, когда длительность импульса сравнима или превышает характерные времена релаксационных процессов в растворителе. Фотохимическая система в этих условиях успевает эволюционировать в ходе возбуждения, а сформированный в результате волновой пакет существенно отличается по форме от пакета, полученного при мгновенной накачке. Граница применимости этого приближения может быть оценена из экспериментальных данных о характерных временах инерционной релаксации среды, являющейся наиболее быстрой среди всех релаксационных компонент полярного растворителя. К примеру, для ацетонитрила (химическая формула CH 3 CN ) время инерционной релаксации составляет ~ 0.19 пс, что делает проблематичным использование приближения мгновенной накачки в ситуациях, когда донорно-акцепторный комплекс возбуждается импульсами длительностью более 100 фс.

Целью настоящей работы является разработка модели фотохимической реакции, в которой динамика оптической накачки системы учитывается явным образом. Основное внимание при этом уделяется адаптации модели к численному моделированию кинетики фотохимического разделения зарядов и рекомбинации ДАК в рамках метода случайных траекторий [2].

1.    Модель и численный метод

Реакцию переноса электрона в полярном растворителе опишем в терминах квантовых переходов между состояниями с различной локализацией электрона. В ДАК такими состояниями являются основное состояние с нейтральными реагентами |DA) и возбужденное состояние с разделенными зарядами |D+A-) (здесь символами D и А обозначены донорный и акцепторный компоненты молекулярной системы). Отметим, что двухуровневое приближение в данном случае используется для упрощения изложения сути метода, и не является принципиальным. Предложенные ниже алгоритмы могут быть напрямую обобщены на системы, содержащие большее количество электронных (и колебательных) состояний, участвующих в фотохимической реакции. Пусть As и AGcr — энергия реорганизации растворителя и свободная энергия электронного перехода |DA) ^ |D+A-). В качестве координат реакции используем маркусовы поляризационные моды Q: (г = 1,...,п). В полярном растворителе электронные термы основного и возбужденного ДАК можно записать в виде п О2

U gA Q ) = Е Q + AG cr , г=1 ^г

U^Q ) = £ (^^ г=1          ^г

где А _г — энергия реорганизации г -й поляризационной моды, V A , = A s .

В приближении сильной связи со средой движение изображающих точек вдоль координат Q i носит характер диффузии. Эволюция функций распределения частиц на термах основного и возбужденного состояний P _gr = P _gr (Q,t) и p _ex = P _ex (Q,t) в этом случае описывается уравнениями

d^   =    к   5 ^   ^ex) (Pgr   Pex) + LexPex,                (2a) dpgr       2^V„2  _,           x            x                                    x d^   =    к   5 (^gr   U ) (Pex   Pgr) + LgrPgr,                  (2b) где Ve — энергия электронной связи донорного и акцепторного состояний, 5 (ж) — функция Дирака, Lk — оператор Смолуховского

^L k

= Ё I ( ^{1 +} (^Q ,  -dQ + ^{Q j}

d ² dQ : ²

т _г — время релаксации г -й моды растворителя, (Q ? ) = 2А _г k B T , Q ^(gr) = 0 , Q^ = 2А _г . Кинетика населенностей электронных состояний ДАК в модели (2) может быть рассчитана через интегралы по конфигурационному пространству от соответствующих плотностей распределения

N _k (t) = I

P k ( Q,t ) dQ,

( k = ex, gr).

Будем считать, что в начальный момент времени система находится в основном электронном состоянии и термодинамически равновесна по ядерным степеням свободы:

P ex ( Q, 0) =0,

^p gr ^(Q, ⁰⁾ = ^p g⁰⁾

= const • exp

(

U gr (Q) к в Т

)

Учтем далее динамику оптического возбуждения ДАК в приближении спектрально широкого импульса, то есть в условиях, когда ширина его спектра существенно превышает величину V 2 A s k B T . В этом пределе мы можем пренебречь различиями в скоростях оптических электронных переходов для частиц, распределенных по конфигурационному пространству и обладающих различными энергиями перехода AU(Q) = U _ex — U gr . Это позволяет описать фотовозбуждение системы дополнительными слагаемыми в уравнениях (2):

dp ex dt dp gr ”dt

^{I (t)}p g⁰⁾ +--^“ el ^{5 (U} gr ^{— U} ex ) ⁽P gr ^— P ex ) + ^I ex p ex -

(6a)

(6b)

^{— I (t)}P g^{0) +}-- ^“ el ^{5 (U} gr ^{— U} ex ) ⁽P ex ^— P gr ) + ^v P gv

Данные уравнения справедливы в слабых электромагнитных полях, когда вероятность фотовозбуждения системы мала и возможно кинетическое описание процесса. В большинстве реальных экспериментов такое приближение оправдано. Величина I (t) в уравнениях (6) имеет смысл скорости оптического перехода |^Л) ^ ^ |D ⁺ A ^- ) . Для гауссова импульса c несущей частотой ш _е и длительностью т _е , /(t) ~ exp (—z^ _e t — t 2 /2T _e 2 ) , функция I (t) имеет вид

I (t) = I ₀ exp

(-T i t

где I ₀ — константа, зависящая от дипольного момента оптического перехода, поляризации электромагнитной волны и т. д. Далее мы положим I ₀ = (у^т _е ) ^{- 1} , что позволяет нормировать пиковую населенность возбужденного состояния ДАК на единицу.

Известно, что наиболее эффективным способом численного решения уравнений стохастической модели в пространстве нескольких координат реакции может считаться метод броуновского моделирования. Метод основан на программной генерации траекторий движения системы на поверхностях свободной энергии химической системы при последовательном учете электронных переходов в моменты рекроссинга гиперповерхностей пересечения термов [2; 3]. В рамках этого подхода оптическое возбуждение ДАК может моделироваться переходами частиц с терма основного состояния на терм состояния с разделенными зарядами в течение действия импульса накачки. Учитывая смысл введенных ранее обозначений, вероятность такого перехо- да на временном интервале (t,t + dt) для отдельной частицы равна dP = I(t)dt, а фотоиндуцированный «прыжок» Ugr(Q) ^ Uex(Q), таким образом, может считаться случайным событием с плотностью распределения вероятности I(t).

Наиболее простым способом генерации оптических переходов в указанной схеме является введение для каждой частицы величины t * , обозначающей момент оптического «прыжка» и выбираемое из ансамбля с плотностью I (t) (здесь а — номер частицы). В рассматриваемом примере такая выборка может быть реализована с помощью любого известного программного генератора псевдослучайных чисел с гауссовым распределением. При этом момент электронного оптического перехода для каждой изображающей точки определяется заранее, на этапе инициализации ансамбля и до начала моделирования диффузионного движения.

Альтернативой может выступить модификация данного алгоритма, в рамках которой решение об электронном «прыжке» с терма основного состояния на терм возбужденного состояния ДАК принимается независимо на каждом шаге по времени. Вероятность P(t1,t2) такого перехода на временном интервале (t1,t2) рассчитывается как t2

^P (М ) = j¹ (t) dt = 2 erf g) - 2 erf g) , t 1

где erf (ж) — функция ошибок (интеграл вероятности). Прыжковые события в этом случае могут моделироваться стандартным для метода Монте-Карло способом: путем сравнения P ( t 1 ,t ₂ ) с псевдослучайной величиной у, полученной от программного генератора с равномерной плотностью распределения на отрезке [0,1] . В случае, если расчетная схема предполагает использование фиксированного шага по времени At , значения P ( t 1 ,t ₂ ) на всех временных интервалах могут быть вычислены на начальном этапе работы программы и сохранены в оперативной памяти.

2.    Тестирование алгоритма. Кинетика фотовозбуждения ДАК в отсутствие рекомбинации зарядов

Последний из описанных алгоритмов был реализован программно в рамках пакета QM2L. Для тестирования работы алгоритма сравним результаты численного моделирования с точным аналитическим решением уравнения (6) в отсутствие рекомбинации. Найдем это решение.

При V e = 0 система (6) распадается на два независимых уравнения для p gr и p _ex . Интегрируем второе уравнение (6) по координатам Q _t и используем введенные ранее определения для населенностей электронных состояний |DA) и ID + А - }

V ex (t)= У I (t) p g0) dQ + j L ex P ex dQ = I ( t ) .

С учетом (7) получим

erf( IV ^{2    2} y^e /

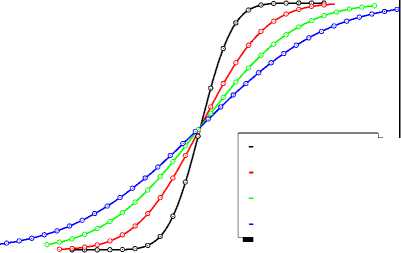
Результаты тестирования работы алгоритма представлены на рисунке 1, где показана кинетика населенности возбужденного состояния донорно-акцепторного комплекса, рассчитанная численно для нескольких значений т _е (указаны на рисунке). Усреднение выполнено по N = = 5•10 5 броуновским траекториям, параметр V e в расчетах положен равным нулю, шаг по времени – 5 фс. Сравнение с аналитическим решением (10) (точки на рис. 1) позволяет говорить о работо

о

Рис.

1.0

0.0

о

о

о

0.5

= 0.05 пс

τ

e

= 0.10 пс

τ

e

= 0.15 пс

τ

e

= 0.20 пс

-0.2

0.0

0.2

время, пс

------те

-0.4

0.4

1. Тестирование расчетного алгоритма. Сплошные

линии — данные численного моделирования кинетики заселения возбужденного состояния ДАК в отсутствие рекомбинации, точки — точный результат (10)

способности алгоритма. Расхождение между численными результатами и решением (10) при указанных параметрах расчета не превышает 1.5 % и обусловлено статистической погрешностью на этапе усреднения по выборке.

3.    Кинетика фотовозбуждения/рекомбинации ДАК

Рассмотрим далее результаты ряда численных экспериментов, в которых оптическая накачка ДАК моделируется наряду с рекомбинацией зарядов донорного и акцепторного компонентов в ходе релаксации растворителя. В расчетах используем модель Йортнера-Биксона [6], принимая во внимание участие высокочастотных (h ^ v >  k B T ) внутримолекулярных колебаний в процессах перераспределения энергии поглощенного фотона. Модель описывается системой нескольких уравнений диффузионного типа, аналогичных уравнениям (2) (см., например, [3]). Предложенные выше алгоритмы численного моделирования электронного оптического возбуждения ДАК при этом могут использоваться без существенных изменений.

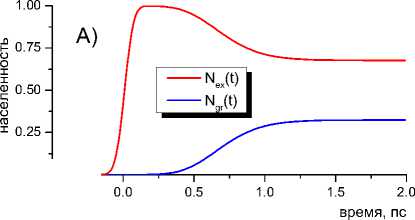
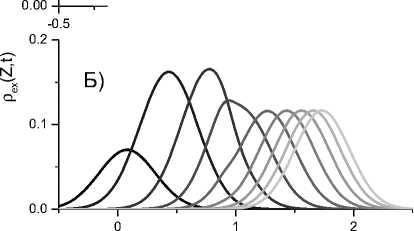
На рисунке 2 показана эволюция населенностей (панель А) и профилей распределения частиц на термах возбужденного (панель Б) и основного (панель В) электронных состояний ДАК, обусловленная действием лазерного импульса, процессами релаксации в растворителе и ДАК, а также обратными электронными переходами. В расчетах использованы следующие значения параметров: энергия реорганизации растворителя A s = 1 эВ, энергия реорганизации высокочастотной внутримолекулярной моды A v = 0 эВ, свободная энергия рекомбинации ДАК AG cr = 0 , энергия электронной связи V e = 0.01 эВ. Время продольной релаксации растворителя T L принято равным 1 пс, время внутримолекулярной колебательной релаксации — T v = 0.03 пс. В качестве абсциссы на панелях Б и В использована коллективная энергетическая координата Z = ^2Q i , выраженная в эВ. Выборка включает N = 5 • 10 5 траекторий.

Результаты на рисунке 2Б демонстрируют динамику образования волнового пакета в возбужденном состоянии ДАК на начальной стадии реакции, далее релаксацию неравновесного пакета к положению равновесия (точка Z = 2 эВ) и его частичный распад в результате горячей рекомбинации зарядов. Эволюция профилей распределения частиц в основном состоянии p gr ( Z, t ) на рисунке 2В показывает образование волнового пакета в окрестности точки пересечения термов Z = 1 эВ и его движение к минимуму поверхности ^-( Z) .

В ситуации, когда оптические переходы |DA) ^ |D + A ^- ) конкурируют с обратными электронными переходами ID + A - } ^ |DA) , длительность импульса накачки может оказывать существенное влияние на кинетику населенностей основного и возбужденного состояний системы. Это предположение иллюстри-

0.10

N t = 0

-----0.25 ПС

-----0.50 пс

-----0.75 пс

-----1.00 пс

-----1.25 пс

1.50 пс

1.75 пс

2.00 пс

0.05

0.00

В)

координата растворителя Z

Рис. 2. А) Кинетика населенностей в модели Йортнера-Биксона. Б), В) Эволюция профилей распределения частиц в возбужденном (Б) и основном (В) состояниях

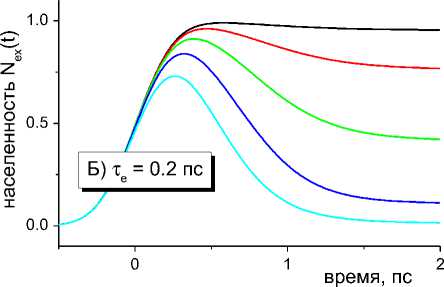
руется результатами численного моделирования, показанными на рисунке 3. На левой панели изображены зависимости N _ex ( t ) , вычисленные при т _е = 0 (в приближении мгновенной накачки), на пра-

вой панели — при т _е = 0.2 пс. Цветом выделены кривые, соответствующие различным V e (указаны на рисунке). Значения других параметров: A s = 1 эВ, A v = 0.3 эВ, h ^ v = 0.1 эВ, AG cr = -0.4 эВ, T L = 1 пс, T v = 0.03 пс. Графики на правой панели рисунка 3 демонстрируют снижение пикового значения населенности возбужденного состояния, обусловленное перекрыванием во времени прямых и обратных переходов. Этот эффект становится более выраженным при увеличении Ki и A v , когда обратные электронные переходы смещаются в область малых Z , где формируется начальный волновой пакет.

Стоит отметить, что влияние параметра т _е на квантовый выход горячей рекомбинации зарядов оказывается слабым. Графики на рисунке 3 показывают, что по завершении процессов релаксации (в момент времени t = 2 t _l = 2 пс) заселение состояния с разделенными зарядами в обоих случаях оказывается одинаковым. Этот результат имеет достаточно простое физическое объяснение. Как было показано ранее в работе [5], вероятность рекомбинации ДАК на сверхбыстрой нетермической стадии в рамках стохастической модели не зависит от формы волнового пакета, а потому не зависит от динамики его образования.

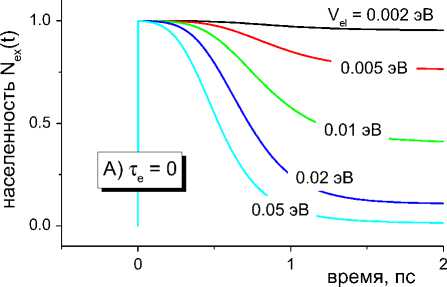
Рис. 3. Кинетика заселения и распада состояния с разделенными зарядами за счет сверхбыстрой рекомбинации ДАК. Левая и правая панели соответствуют различным значениям длительности импульса накачки (указаны в графиках)

Заключение

При описании сверхбыстрых фотохимических реакций в ДАК, протекающих на временах, сравнимых с временами релаксации растворителя, важным является последовательный учет динамики заселения возбужденного состояния при взаимодействии ДАК с лазерным импульсом. Это дает более подробную картину реакции и позволяет точнее интерпретировать результаты экспериментов. Данная работа затрагивает вычислительные аспекты моделирования процессов оптической накачки ДАК. Основными результатами работы являются кинетическая модель реакции, использующая единый подход к описанию прямых и обратных электронных переходов, а также алгоритмы численного моделирования оптических переходов в рамках метода случайных траекторий [2–4]. Несмотря на то что все результаты сформулированы для двухуровневой системы, они могут быть легко адаптированы для систем, включающих несколько электронных и высокочастотных колебательных состояний.

Предложенные в работе алгоритмы реализованы программно в качестве модуля расширения вычислительного пакета QM2L. Результаты тестовых расчетов, а также сравнение данных численного моделирования и точных решений модельных уравнений в частных случаях подтверждают работоспособность алгоритмов.

Главным ограничением предложенной модели с физической точки зрения является использование приближения спектрально широкого импульса. Это приближение позволяет пренебречь различиями в скоростях оптических переходов для частиц в разных точках конфигурационного пространства, однако сужает область применимости модели. Модель справедлива в случае, когда спектральная ширина сигнала значительно превышает k B T . В частности, для гауссова импульса с постоянной несущей частотой условием применимости будет выражение

A s ^ b T< к²^. (11)

При комнатных температурах и сверхкоротких импульсах длительностью т2 = 10 фс это соотношение дает оценку для энергии реорганизации среды As < 0.172 эВ. Таким образом, модель может применяться для описания фотохимических процессов в слабополярных растворителях, либо при использовании спектрально уширенных импульсов (например, в результате чирпирования). На последующих этапах работы мы предполагаем развить данный подход и разработать модели, учитывающие спектральный состав импульса накачки.