Компьютерное моделирование влияния кристаллографии структуры на гофрообразование при вытяжке

Как известно, такие широко распространенные в производстве аэрокосмической техники полуфабрикаты как листы, ленты, профили, трубы и т.д. обладают явно выраженной анизотропией свойств. Игнорирование в технологических расчетах анизотропии свойств не только снижает потенциальные деформационные возможности заготовок, но и приводит к целому ряду других нежелательных явлений: повышенному расходу металла, ограничению предельно допустимой деформации, искажению формы, размеров и снижению эксплуатационных параметров продукции [1-6]. С другой стороны, рациональная анизотропия является серьезным фактором интенсификации процессов формообразования материалов и повышения эксплуатационных характеристик изделий в определенных направлениях [4-11].

Оптимальную анизотропию свойств для конкретного процесса можно определить методами компьютерного моделирования, современный уровень развития которых позволяет значительную часть работ по оценке и анализу напряженно-деформированного состояния перенести в область численного эксперимента; получить больший объем информации; провести всестороннее исследование не только процессов формообразования, но и характера поведения материала в этих процессах в зависимости от его структурного состояния; рассмотреть и сопоставить большее количество альтернативных вариантов [12-14].

PAM-STAMP 2G, AUTOFORM и др., в большинстве случаев полностью не востребованы, т.к. используемые в них алгоритмы и модели или предназначены для изотропных материалов, или основываются на теории пластичности анизотропных сред, в исходные уравнения которой не входят в явном виде параметры кристаллографической ориентации структуры и константы кристаллической решетки, являющиеся причиной возникновения анизотропии свойств [15-18]. Следовательно, нет и оснований для непосредственного анализа поведения металла в конкретной операции, определения условий формирования и наиболее эффективного использования направленности свойств заготовок.

Учесть кристаллографическую ориентацию структуры и сформулировать требования к ней позволяет разработанный в [19-20] критерий пластичности, особенностью которого является то, что в него в явном виде входят параметры кристаллографической ориентации структуры и константы кристаллической решетки. На основе данного критерия была разработана и интегрирована в программу LS-DYNA модель материала [21-22], что позволило проводить анализ процессов пластического деформирования с учетом кристаллографической ориентации структуры заготовок.

Используя данную модель материала, можно изучить влияние кристаллографической ориентации структуры на гофрооборазование при вытяжке. Известно, что в процессе вытяжки во фланце заготовки при определенных соотношениях ее размеров (при большой степени деформации и небольшой толщине материала) и механических свойств возникают волны или складки в радиальном направлении [23]. Появление складок приводит к резкому увеличению сопротивления фланца деформированию вследствие повышения изгибающих напряжений при перемещении складок по вытяжной кромке матрицы. Кроме того, возникают дополнительные напряжения, необходимые для распрямления складок в вытяжном зазоре. Суммарное влияние указанных факторов обуславливает в итоге отрыв фланца от стенки изделия. В связи с этим для устранения гофрообразования применяется прижим заготовки складкодержателем, усилие которого определяется в том числе и свойствами материала.

Поэтому в данной статье на примере вытяжки колпачков из алюминиевого сплава 8011А исследовано влияние кристаллографии структуры материала на гофрооборазование и минимально допустимое усилие прижима.

КОМПЬЮТЕРНАЯ МОДЕЛЬ ПРОЦЕССА ВЫТЯЖКИ

Схема вытяжки колпачка из алюминиевого сплава 8011А со всеми характерными размерами приведена на рис. 1. С целью сокращения количества конечных элементов моделировалось ¼ объема, заключенного между координатными плоскостями YOX и YOZ. Ось Z совпадает с направлением прокатки. Тип конечных элементов для всех частей модели – 4-х узловые оболочечные элементы SHELL163 с 5 и 3 точками интегрирования по толщине заготовки и инструмента соответственно. Длина ребра конечно-элементной сетки заготовки составляет 0,35 мм, инструмента – 0,7 мм.

К прижиму в направлении оси Y приложено постоянное усилие, величина которого подбиралась опытным путем таким образом, чтобы отсутствовало гофрообразование. Пуансон перемещается с постоянной скоростью 2 м/с по направлению оси Y, матрица – неподвижна.

Деформирующий инструмент принимался абсолютно жестким. Коэффициент трения принят равным 0,08 (по закону Кулона).

При моделировании задавались следующие свойства материала заготовки – алюминиевого сплава 8011А: предел прочности – 140 МПа; предел текучести – 130 МПа; относительное удлинение – 3%; модуль Юнга – 70 ГПа; коэффициент Пуассона – 0,3 [24].

С целью оценки влияния кристаллографии структуры на гофрообразование при вытяжке моделировался анизотропный материал, текстура которого состоит только из одной идеальной кристаллографической ориентировки. Рассмотрены три ориентировки {111}<112>, {100}<100> и {124}<123>, параметры которых приведены в табл. 1. Как видно из табл. 1, кристаллографическая ориентировка {111}<112> обеспечивает выравнивание коэффициентов поперечной деформации в плоскости листа, т.е. данный материал является трансверсальноизотропным. Также для сравнения выполнено моделирование процесса вытяжки колпачка из изотропной заготовки.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

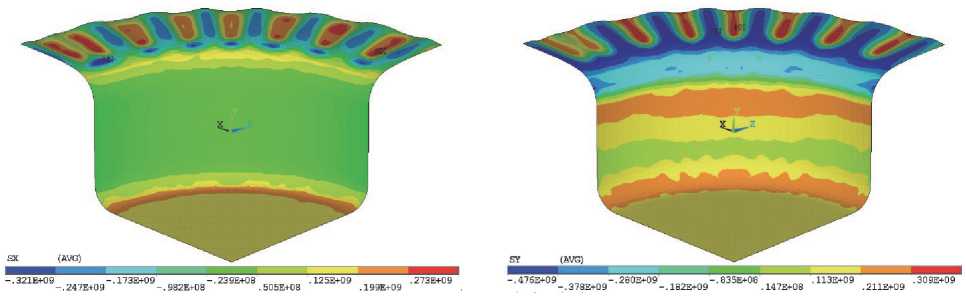
В ходе моделирования установлено, что как для изотропной заготовки, так и для трансверсально-изотропной заготовки (идеальная кристаллографическая ориентировка {111}<112>), минимальное усилие прижима, при котором устраняется гофрообразование, составляет 0,42 Н/мм2 или 600 Н. При этом, как видно из рис. 2, потеря устойчивости фланца заготовки происходит под действием напряжений тангенциального сжатия.

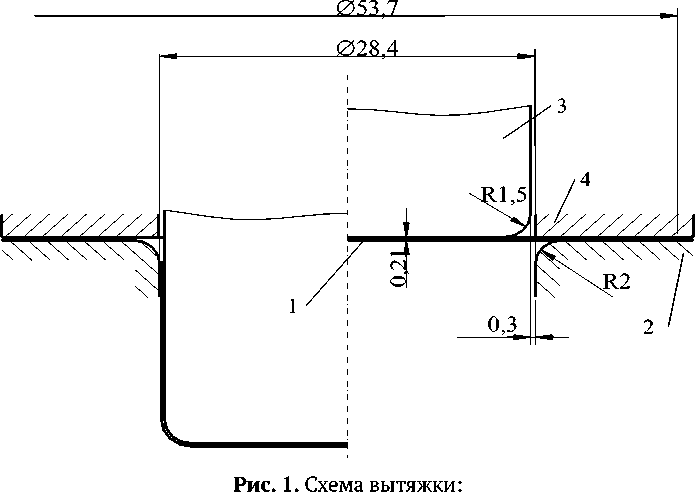
1 – заготовка; 2 – матрица; 3 – пуансон; 4 – прижим

Таблица 1. Кристаллографические ориентировки и их параметры

Идеальная ориентировка	Ориентационные факторы			Коэффициенты поперечной деформации			Примечание
	А 1	А 2	А 3	Д о	Д |5	Д 90
{111}<112>	0,250	0,250	0,333	0,628	0,628	0,628	Трансверсальноизотропный материал
{100}<100>	0	0	0	0,500	0,117	0,500	Фестоны под углом 0/90° к направлению прокатки
{124}<123>	0,250	0,250	0,190	0,409	0,555	0,409	Фестоны под углом 45° к направлению прокатки
-	0,200	0,200	0,200	0,500	0,500	0,500	Изотропный материал

б

а

Рис. 2. Гофрообразование при вытяжке изотропной заготовки с удельным усилием прижима менее 0,4 Н/мм²: а - радиальные напряжения; б - тангенциальные напряжения

При вытяжке же заготовок, текстура которых состоит только из одной ориентировки {100}<100> и {124}<123>, требуются более высокие усилия прижима: 0,83 Н/мм2 или 1,2 кН. Это можно объяснить влиянием следующих факторов.

Во-первых, неравномерным распределением давления прижима по фланцу заготовки. Это вызвано тем, что утолщение краевой части фланца по периметру вследствие плоскостной анизотропии различно. Следовательно, усилие прижима сосредоточено в тех участках краевой части фланца, в которых коэффициенты поперечной деформации минимальны, а значит, возникает наибольшее утолщение.

Во-вторых, влияние кристаллографии структуры на гофрообразование сказывается потому, что она определяет значение и соотношение радиальных и тангенциальных напряжений, а, следовательно, и силы, вызывающие выпучивание, а также внутренние силы и моменты, препятствующие ему.

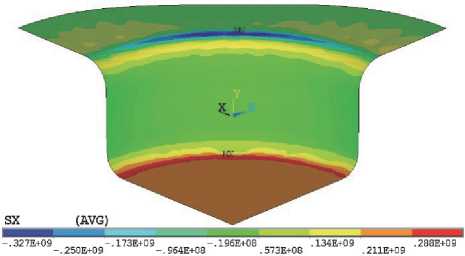
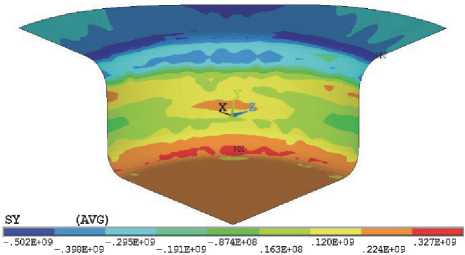
Как видно из рис. 3, при вытяжке осесимметричных деталей волнистость образуется в первую очередь в тех местах фланца, где действуют

а

б

Рис. 3. Момент начала гофрообразования при вытяжке анизотропной заготовки

с ориентировкой {100}<100> с удельным усилием прижима менее 0,8 Н/мм2: а - радиальные; б - тангенциальные напряжения максимальные тангенциальные напряжения сжатия, т.е. там, где коэффициенты поперечной деформации в плоскости листа имеют минимальное значение, а значит, формируется впадина.

ЗАКЛЮЧЕНИЕ

Таким образом, по сравнению с изотропным и трансверсально-изотропным материалом для устранения гофрообразования при вытяжке заготовок с плоскостной анизотропией требуются более высокие усилия прижима. При этом складки образуются в тех местах фланца, где начинает формироваться впадина, т.е. там, где коэффициенты поперечной деформации минимальны.