Компьютерное нахождение четырехэлементных мультипликативно идемпотентных полуколец

Данная статья является продолжением работы [2], в которой вручную найдены все трехэлементные полукольца с идемпотентным умножением и описаны их свойства.

В работе [6] с помощью компьютера описаны все трехэлементные аддитивно идемпотентные полукольца, с точностью до изоморфизма (таких полуколец ровно 61).

Общая теория полуколец изложена в монографии Голана [4]. Мультипликативно идемпотентным полукольцам посвящены работы [1–3, 5].

Полукольцом называется алгебраическая структура     ⟨S, +, ⋅⟩     с     коммутативно ассоциативной операцией сложения + и ассоциативной операцией умножения, дистрибутивной относительно сложения с обеих сторон.

Полукольцо S называется:

• -    коммутативным , если S удовлетворяет тождеству xy=yx ;

  
  
  

  Эта работа © 2022 Михеев Р. А., Петров А. А. лицензируется под CC BY 4.0. Чтобы просмот-

  
  

  реть копию этой лицензии, посетите

  
  

• -    мультипликативно идемпотентным ( аддитивно идемпотентным ), если на нем тождественно хх = x (соответственно, х + x = x );

• -    идемпотентным , если S одновременно мультипликативно и аддитивно идемпотентное;

• -    моно-полукольцом , если x+y=xy для всех x , y е S ;

• -    полукольцом с константным сложением , если оно удовлетворяет тождеству x+y=u+v .

Элемент 0 произвольного полукольца S назовем поглощающим по умножению ( поглощающим по сложению ), если для всех xеS выполняется 0 x = x -0=0 (соответственно, x +0=0). Элемент да е S , поглощающий по сложению и по умножению, называется поглощающим .

Если в полукольце S существует элемент 0, нейтральный по сложению и поглощающий по умножению, то S называется полукольцом с нулем 0. Если же полукольцо S обладает элементом 1, нейтральным по умножению, то S называется полукольцом с единицей 1.

Отметим, что к любому полукольцу S можно естественным образом присоединить нулевой элемент 0 или поглощающий элемент да. Обозначим полученные полукольца S и {0} и S и { да } , соответственно.

Хорошо известно, что с точностью до изоморфизма существует ровно шесть двухэлементных мультипликативно идемпотентных полуколец:

• •    двухэлементная цепь B ={0,1};

• •    двухэлементное поле Z 2 ={0,1};

• •    двухэлементное идемпотентное монополукольцо D ={1,да} с единицей 1;

• •    двухэлементное полукольцо T ={1,∞} c единицей 1 и константным сложением ( x + у =да);

• •    двухэлементное идемпотентное полукольцо L ={ a , b }, с тождеством xy=x ;

• • двухэлементное идемпотентное полукольцо R ={ a , b }, с тождеством xy=y .

Для любого полукольца ( S , +, ■ ) существует антиизоморфное полукольцо ( S , +, * ), в котором тождественно x ∗ y = y ⋅ x ; такое дуальное полукольцо обозначим через S*.

Полукольцо S , для которого S* ≅ S , назовем самодуальным . Ясно, что любое коммутативное полукольцо S самодуально. В работе [2] установлено, что среди трехэлементных некоммутативных мультипликативно идемпотентных полуколец самодуальных нет.

Пример 1. Положим S = LxR . Умножение на некоммутативном четырехэлементном мультипликативно идемпотентном полукольце S выполняется следующим образом:

( x , у ) ■ ( и , v ) = ( xu , yv ) = ( x , v ) для любых x , у , и , v е { a , b }.

Соответственно, сложение на полукольце S *, дуальном к S , задается так же, как на S , а умножение определяется правилом:

( x , у ) * ( и , v ) = ( и , v ) ■ ( x , у ) = ( и , у ), и, как легко видеть, S * s R*L s LxR= S , то есть S - некоммутативное самодуальное мультипликативно идемпотентное полукольцо.

Для описания всех четырехэлементных мультипликативно идемпотентных полуколец S нами составлена компьютерная программа на языке программирования С.Опишем схему создания этой программы.

Аддитивный и мультипликативный редукты полукольца задаются с помощью таблиц Кэли. Таблицы представляют собой одномерные массивы matrix длины N2 из элементов 0, ..., N-1, в которых с 0-ого по (N-1)-ую позицию занимает первая строка таблицы, с N-ного по (2N-1)-й - вторая строка таблицы и т. д. Соответственно, позиция элемента в строке i и столбце j в массиве matrix равна i*N + j.

Шаг 1. Генерация ассоциативных таблиц

//проверка таблицы на ассоциативность bool isassociative(int matrix[N*N]) { for (int i = 0; i < N; i++) { for (int j = 0; j < N; j++) { for (int k = 0; k < N; k++) { if (matrix[matrix[i*N + j]*N + k] != ma-trix[i*N + matrix[j*N + k]])

return false;

}

}

} return true;

}

//Создание аддитивной полугруппы полукольца S с учетом ее коммутативности void generate_commutative_tables(List* mult_tables) { int matrix[N*N];

generate_commutative_tables_rec(matrix, 0, 0, mult_tables);

if (isassociative(matrix)) { int* matrix_copy = copy_matrix(matrix); list_push(add_tables, matrix_copy);

} return;

} for (int i = 0; i < N; i++) { matrix[row_pos*N + col_pos] = i; matrix[col_pos*N + row_pos] = i; int new_row_pos = row_pos;

if (col_pos == N - 1) new_row_pos++;

int new_col_pos = (col_pos +  1  + new_row_pos) % N;

gener- ate_commutative_tables_rec(matrix, new_row_pos, new_col_pos, add_tables);

}

}

//Создание мультипликативно идемпотентной полугруппы void generate_idempotent_tables(List* mult_tables) { int matrix[N*N];

for (int j = 0; j < N; j++) { matrix[j*N + j] = j;

} generate_idempotent_tables_rec(matrix,

0, 1, mult_tables);

if (isassociative(matrix)) { int* matrix_copy = copy_matrix(matrix); list_push(mult_tables, matrix_copy);

} return;

} for (int i = 0; i < N; i++) { matrix[row_pos*N + col_pos] = i;

int new_col_pos = (col_pos + 1) % N;

int new_row_pos = row_pos;

if (new_col_pos == 0) new_row_pos++;

if (new_col_pos == new_row_pos) { new_col_pos = (new_col_pos + 1) % N; if (new_col_pos == 0) new_row_pos++;

} generate_idempotent_tables_rec(matrix, new_row_pos, new_col_pos, mult_tables);

}

}

Шаг 2. Проверка дистрибутивности умножения относительно сложения для построенных таблиц Кэли

//Проверка левой дистрибутивности bool isdistributive(int mult[N*N], int add[N*N]) { return isdistributive_left(mult, add) & isdistributive_right(mult, add);

} bool isdistributive_left(int mult[N*N], int add[N*N]) { for (int i = 0; i < N; i++) { for (int j = 0; j < N; j++) { for (int k = 0; k < N; k++) { if (mult[i*N + add[j*N +  k]]  != add[mult[i*N + j]*N + mult[i*N + k]])

return false;

}

}

} return true;

} bool isdistributive_right – правая дистрибутивность проверяется аналогично левой

// Проверка коммутативности умножения. Если умножение коммутативно, проверяем только левую дистрибутивность умножения относительно сложения.

bool iscommutative(int table[N*N]) { for (int i = 0; i < N; i++) { for (int j = i; j < N; j++) { if (table[i*N + j] != table[j*N + i]) return false;

}

} return true;

tive_left(mult_temp->value, add_temp->value)

Semiring* semiring = (Semir-ing*)malloc(sizeof(Semiring));

semiring->mult = mult_temp->value;

semiring->add = add_temp->value; list_push(semirings, semiring);

} add_temp = add_temp->next;

} mult_temp = mult_temp->next;

}

}

Шаг 3. Выбор из полученного списка неизоморфных полуколец

// Генерируем одномерные массивы – перестановки чисел 0, ..., N-1.

void generate_arrays(List* arrays) { int array[N];

generate_arrays_rec(array, 0, arrays);

} void generate_arrays_rec(int arr[N], int pos, List* arrays) { if (pos == N) { list_push(arrays, copy_array(arr));

} else { for (int i = 0; i < N; i++) { bool found = false;

for (int j = 0; j < pos; j++) { if (arr[j] == i) { found = true;

break;

}

} if (found)

continue;

arr[pos] = i;

generate_arrays_rec(arr, pos + 1, arrays);

}

}

}

//Перебираем пары полуколец, проверяя свойства f ( a⋅b ) = f ( a ) ⋅f ( b ) , f ( a+b ) = f ( a ) +f ( b ) для произвольной подстановки f на множестве {0, 1, ., N-1}. Если для некоторой пары полуколец s1 и s2 существует f с перечисленными свойствами, то s1 и s2 изоморфны.

return false;

}

} return true;

} bool areisomorphic(Semiring s1, Semiring s2, List arrays) { bool result = false;

while (temp != NULL) { if (isisomorphism(temp->value, s1, s2)) return true;

temp = temp->next;

} return false;

}

//Перебираем список полученных полуколец и исключаем изоморфные полукольца void filter_isomorphism(List* semirings, List arrays) { struct Node* temp = semirings->head;

while (temp != NULL) { struct Node* temp_inner = temp->next;

while (temp_inner != NULL) { if (areisomorphic(*((Semiring*)temp->value), *((Semiring*)temp_inner->value), arrays)) { struct Node* temp_next = temp_inner->next;

list_delete(semirings, temp_inner); temp_inner = temp_next;

} else temp_inner = temp_inner->next;

} temp = temp->next;

}

}

Шаг 4. Проверка свойств найденных мультипликативно идемпотентных полуколец

//идемпотентность bool isidempotent(int matrix[N*N]) { for (int i = 0; i < N; i++) { if (matrix[i*N + i] != i) return false;

} return true;

}

//наличие нейтрального элемента 1 относительно умножения int neutral(int matrix[N*N]) { for (int i = 0; i < N; i++) { if (isneutral(matrix, i)) { return i;

}

} return -1;

} bool isneutral(int matrix[N*N], int inx) { for (int i = 0; i < N; i++) { if (matrix[inx*N + i] != i || matrix[i*N + inx] != i) { return false;

}

} return true;

}

//наличие нейтрального элемента 0 относительно сложения int zero(int mult[N*N], int add[N*N]) { int add_neu = neutral(add);

if (add_neu == -1) { return -1;

} for (int i = 0; i < N; i++) { if (mult[add_neu*N + i] != add_neu || mult[i*N + add_neu] != add_neu) { return -1;

}

} return add_neu;

}

//наличие поглощающего элемента int infinity(int mult[N*N], int add[N*N]) { for (int i = 0; i < N; i++) { if (isinfinity(mult, add, i)) { return i;

}

} return -1;

} bool isinfinity(int mult[N*N], int add[N*N], int inx) { for (int i = 0; i < N; i++) { if ( mult[i*N + inx] != inx || mult[inx*N + i] != inx

|| add[i*N + inx] != inx || add[inx*N + i] != inx

) { return false;

}

} return true;

}

//проверка константности сложения bool isconst(int table[N*N]) { for (int i = 0; i < N*N - 1; i++) { if (table[i] != table[i + 1]) { return false;

}

} return true;

}

//проверка, является ли полукольцо моно-полукольцом bool ismono(int mult[N*N], int add[N*N]) { for (int i = 0; i < N*N; i++) { if (mult[i] != add[i]) { return false;

}

} return true;

}

Шаг 5. Переобозначение элементов полукольца

Обозначаем элементы полученных полуколец через a, b, c, d и т. д. Нулевой, единичный и поглощающий элементы обозначаем как 0, 1 и i, соответственно. Полученный результат записывается в текстовый файл (рис. 1): comm idem mono const zero one inf add mult +   --   +   --   + iiii iaii iiii iibi add mult +  -----  + iiii iaii iiii iibi add mult +   ____   _   _ aaca aaaa aaca abaa ccac aaca aaca aaad

Рис. 1

Полный исходный код описанной программы доступен по ссылке:

При N=3 получен результат из [2, теорема 1]: с точностью до изоморфизма существует ровно 43 трехэлементных мультипликативно идемпотентных полукольца, среди которых:

• •    19 коммутативных полуколец, из них 7 идемпотентных;

• •    23 идемпотентных полукольца, в том числе 16 некоммутативных;

• •    14 полуколец с единицей 1, 6 полуколец с нулем 0, 4 полукольца имеют одновременно 0 и 1;

• •    12 полуколец с поглощающим элементом ∞, 5 полуколец с 1 и ∞.

При N=4 результатом работы программы стала следующая

Теорема 1. С точностью до изоморфизма существует ровно 381 четырехэлементное мультипликативно идемпотентное полукольцо. Среди этих полуколец:

• •    118 коммутативных, из них 33 идем-потентны;

• •    166 идемпотентных;

• •    46 полуколец с нулем 0;

• •    67 полуколец с единицей 1;

• •    17 полуколец с 0 и 1;

• •    78 полуколец с поглощающим элементом ∞, из них 20 имеют 1;

• •    15 полуколец с константным сложением;

• •    5 полуколец являются монополукольцами .

Замечание 1. Время работы созданной программы для поиска всех четырехэлементных мультипликативно идемпотентных полуколец на персональном компьютере с процессором AMD FX - 4300 составляет 2,73 секунды. Следует заметить, что программа основана на большом переборе вариантов, поэтому уже при N=5 она не дает требуемый результат за разумное время.

В дальнейшем планируется усовершенствование алгоритма для сокращения времени ее работы.

Замечание 2. Мультипликативная полугруппа полукольца с коммутативным идемпотентным умножением является нижней полурешеткой, то есть частично упорядоченным множеством (a≤b⇔ab=a), для каждой пары a, b элементов которого имеется точная нижняя грань inf{a,b}=ab. С точностью до изоморфизма существует 5 четырехэлементных нижних полурешеток (рис. 2):

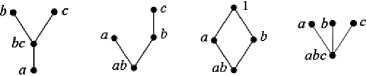
(1) (2) (3) (4) (5)

Рис. 2

Из 118 полуколец с коммутативным идемпотентным умножением 37 полуколец с умножением (1), 27 полуколец с умножением (2), 34 полукольца с мультипликативной полурешеткой (3) и по 10 полуколец типа (4) и (5).

Заметим, что с точностью до изоморфизма существует ровно 15 пятиэлементных нижних полурешеток. Поэтому поиск всех неизоморфных пятиэлементных коммутативных мультипликативно идемпотентных полуколец можно начинать с подбора аддитивной коммутативной полугруппы для каждой из нижних полурешеток по умножению.

Замечание 3. Присоединяя внешним образом к полученным в теореме 1 четырехэлементным полукольцам нулевой элемент 0 (поглощающий элемент ∞), получим 381 пятиэлементное мультипликативно идемпотентное полукольцо с 0 (соответственно, с ∞).

Пусть S – произвольное пятиэлементное мультипликативно идемпотентное полукольцо с нулем 0. Известно [1, теорема 4.1.1], что S представимо в виде прямой суммы некоторых булева кольца R и антикольца T (напомним, что антикольцом называется полукольцо, удовлетворяющее квазитождеству x+y =0⇒ x =0). Но любое неодноэлементное конечное булево кольцо изоморфно прямому произведению двухэлементных полей, а потому имеет четное число элементов. Значит, R ={0}, и S = T – антикольцо. Если при этом в S нет делителей нуля (то есть ab ≠0 для любых a , b ∈ S \{0}), то S \{0} будет четырехэлементным полукольцом.

Стало быть, нахождение всех пятиэлементных мультипликативно идемпотентных полуколец S с нулем сводится к случаю, когда S имеет ненулевые делители нуля.