Комплексная численная модель медленного течения многофазной жидкости

В настоящее время модели механики многофазных сред широко используются во многих областях геофизики: седиментологии, динамике магмы и углеводородов, сейсмологии, тектонике [1–4]. Многофазной средой называют континуум (смесь), состоящий из нескольких компонентов (фаз), каждый из которых заполняет один и тот же объем, занятый смесью, и имеет собственную скорость [3]. По сравнению с однофазными, построение моделей многофазных сред значительно сложнее, потому что необходимо учитывать межфазное взаимодействие (в частности тепло- и массообмен между фазами), а уравнения, описывающие его, содержат множество неопределенных параметров, значения которых можно найти только после введения дополнительных предположений и ограничений [4]. Задача еще значительнее усложняется в случае, когда нужно рассматривать процессы, в которых приходится иметь дело с комплексами, состоящими из нескольких разнородных сред и учитывать их взаимовлияния на подвижных границах и условия их сопряжения. Даже для самых простых структур такого рода построение численных моделей является нетривиальной задачей [5].

При исследовании глубинных процессов в земной коре и мантии значение имеет моделирование аккумуляции разуплотненного мантийного вещества на границе «земная кора-мантия». Такие зоны разуплотнения зафиксированы геофизическими и сейсмическими наблюдениями в недрах большинства тектонически активных областей, например, под корой активной зоны перехода океан-континент. Существуют различные гипотезы их образования: концентрация легкого материала под корой; адвекция из мантии [6] как результат мантийного диапиризма [7] и другие. Разработанные к настоящему времени модели отображают лишь отдельные аспекты процесса аккумуляции: или моделируется адвекция легкого вещества в мантии без взаимодействия с покрывающей корой [6], последняя заменяется простым граничным условием; или закон поступления легкого вещества предполагается заданным [8]; или рассматривается эволюция легкой линзы без учета источника поступления вещества [7]. В этой связи актуальной проблемой является разработка численных моделей, дающих представление об эволюции указанного выше процесса в комплексе.

В работе [9] построена комплексная численная модель, в которой для описания течения в расчетной области, состоящей из толстого вязкого слоя, покрытого тонким многослойным вязким пластом, использовались разные уравнения: в толстом слое — уравнения Стокса, а в тонком многослойном пласте — уравнения Рейнольдса. Методом асимптотических разложений получено уравнение, связывающее смещения границ слоев многослойного пласта со скоростями на его нижней границе. Результаты моделирования показали, что включение в модель этого уравнения в качестве дополнительного условия позволяет, во-первых, получить численное решение с хорошей точностью, устойчивое к возмущениям границ слоев, а во-вторых, вести счет с более крупным шагом по времени, что существенно сокращает вычислительные затраты.

В настоящей работе проведено численное моделирование разуплотнения в виде легкой линзы. Расчетная область состояла из двухфазной вязкой среды, покрытой тонким многослойным вязким пластом. Процесс рассматривался при больших деформациях границ слов. Показаны возможные приложения результатов вычислений в исследовании Западно-Тихоокеанской зоны перехода океан-континент. Модельные исследования механизма образования активных океанических окраин являются одной из основных проблем глобальной тектоники, так как для глубокого и всестороннего изучения процесса аккумуляции разуплотненного мантийного вещества на границе «земная кора–мантия» необходимы не только качественные представления, но и количественные характеристики глубинных движений и распределения напряжений. Помимо теоретического интереса эти работы имеют и практическое значение для изучения закономерностей формирования месторождений полезных ископаемых и углеводородов.

2.    Система уравнений и краевые условия Рис. 1. Общая схема расчетной области: сплошными линиями показаны границы вязкого пласта; отрезки с маркерами изображают поток легкой фазы на нижней границе для описания течения в Dx  уравнения

Рассмотрим расчетную область (Рис. 1), которую разделим на две подобласти: D_Y и D ₂. Верхняя подобласть D представляет собой относительно тонкий пласт, состоящий из N вязких слоев с плотностями р_; и вязкостями ц . Обозначим через Z₍ границы слоев, где i = 1, N + 1 Нижняя подобласть D заполнена двухфазной вязкой средой, в которой тяжелая фаза с плотностью р₅ и вязкостью ц составляет основную долю, а легкая фаза с плотностью Ру и вязкостью Цу имеет небольшую объемную концентрацию ф . На нижней границе расчетной области задан фильтрационный поток легкой фазы.

Так как горизонтальный размер многослойного пласта существенно больше вертикального, можно предположить, что горизонтальные скорости течения в нем значительно больше вертикальных. Это дает возможность применить Рейнольдса — упрощенные уравнения в длинноволновом приближении, которые получены из уравнений Навье-Стокса при следующих предположениях:

• -    характерный горизонтальный масштаб возмущений много больше вертикального;

• -    плотность не убывает с глубиной;

• -    негидростатические напряжения существенно меньше гидростатического давления:

p ,1     ^Ц i u 1,22 ,

Р,2 = -Pig     (i = 1, N + 1), где g — ускорение силы тяжести, p — давление, и — скорость жидкости. Здесь и далее нижний индекс «, к » обозначает частную производную по координате xk (к = 1,2), а «, t» — производную по времени t.

Поле скоростей из (1) должно удовлетворять уравнению неразрывности u1,1 + u 2,2   0

и следующим граничным условиям:

p = 0, Pj и ₂ = 0, z = Z j,

[ и , ] + = 0,     [ p ] + = 0,     [P 1 U 1,2 ] + = 0, z = Z i    ( i = 1, N + 1).

Зададим начальное положение границ слоев пласта:

Z ( Х 1 ,0 ) = Z i0

( i = 1, N + 1).

Кроме этого, предположим, что подвижные границы Z_t являются непроницаемыми. Тогда изменение толщин слоев h = Z - Z_/+1 происходит только за счет перетекания жидкости внутри слоя. Однако на границе сопряжения подобластей происходит перетекание легкого компонента из D, в нижний слой пласта и обратно с объемным потоком V . Тогда кинематическое условие можно записать следующим образом:

^hN , t

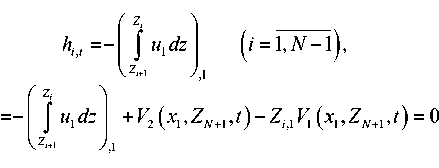
j и 1 dz       ( i = 1, N - 1 )

Z_M       J ,1

h j U1 dz + V. (X1,Zn+1,t)-Zi,1V1 (X1,Zn+1,t) = 0.

Решив уравнения (1), (2) с учетом условий (3)-(5), определим значения и ,, и₂ и p на границах слоев. После подстановки их в (5) и некоторых преобразований получим уравнения относительно границ слоев Z :

(i = 1, N),(6)

где A„ = A-= f У hi У h. У— -— к    , 8j — символ Кронекера (i < j, i, j = 1, N).

j     j           m=j jk=jpк1 + 8ik +8ij

На боковых границах области D, поставим условия отсутствия потока жидкости, которые имеют следующий вид: Zj j = 0.

Для описания движения двухфазной среды в нижней подобласти D₂ можно использовать уравнения вязкой компакции, которые моделируют поровязкие процессы, представляющие собой совместную деформацию двухфазной среды и фильтрацию флюида (легкого компонента) сквозь вязкий скелет (тяжелый компонент) [1 -4]:

(р$ (икj + иьi)) _ - p i - (р$ (1- ф) + рf ф)g8i2 = 0,

—p-i-PT V-Р fg 8'2 = 0    (' = 1,2),

где к — проницаемость скелета, и₁ — скорость скелета, V — поток флюида (относительно скелета), p — давление.

В достаточно быстрых процессах давления в фазах могут быть различными (см., например, [2]). Однако в медленных процессах, рассматриваемых в настоящей работе, фазы находятся в состоянии, близком к механическому равновесию, и скачок давления на межфазной границе можно считать пренебрежимо малым [3]. Плотности и скорости фаз, входящие в (7), должны удовлетворять закону сохранения массы:

(p.(1-ф)),t +(р. (1-ф)u,),- =р,,t (1 -ф) + р,,i (1-ф)и

-

р, ф, t +р, ((1-Ф) ui) = 0,

(рf ф),, +(рf (фui + V)),=рf,tф+рf,i (фu- + V)+рfф,t +рf (фui + V),i = 0.

Предположим, что плотности фаз при движении не изменяются:

p , , t + р , ,i u i = ^0,

f V)  „

p,, + p,,  u, + —  = 0.

^f , t        , ^       ф J

Подставив (9) в закон сохранения массы (8), предварительно сократив, соответственно, на р$ и получим:

р f , тогда

Сложим уравнения (10):

-ф, t +((1 -ф) ui), i = 0, Ф,t +(Ф Ui + Vi),i = 0.

u i , i + V , i = 0.

Уравнение (11) характеризует баланс объемного содержания компонент.

В данной работе для вычисления проницаемости скелета к применялась формула [7]:

к = H2ф2/(72п),

где H — толщина слоя D . Эволюция объемной концентрации флюида описывалась одним из уравнений (10), например, первым:

^ф , t ^+ф , i U = ( 1 ^-ф ) U , i .

Теперь, имея уравнения (7)–(11), можно конкретизировать скорость относительного движения тяжелой и легкой фаз.

Так как единый закон движения фаз в недрах Земли пока еще математически не сформулирован, при построении моделей используется несколько вариантов. Например, двухкомпонентная среда, часто употребляемая при моделировании седиментационной конвекции [6], представляется как вязкая жидкость, содержащая взвесь твердых частиц, совокупность которых в гидродинамическом приближении может рассматриваться как жидкость, а смесь — как двухкомпонентная среда. Для учета адвективных процессов в ней прибегают к диффузионному (одножидкостному) приближению.

Построенная выше система уравнений (7)–(12) позволяет описать движение такой двухкомпонентной среды, потому что уравнения диффузионного приближения сводятся к уравнениям вязкой компакции, если сделать следующие уточнения [10]:

• –    частицы движутся под действием градиента давления, а не силы тяжести;

• –    скорость движения частицы определяется относительно вмещающей жидкости, а не центра масс смеси.

На боковых границах расчетной области зададим условия гладкой неподвижной стенки:

^U 1    ⁰, V   ⁰,     Ц N +1 ( ^U 1,2 ^{+ U} 2,1 )    ⁰ ,

а на нижней границе (скелет неподвижен) — флюидный поток:

U -lz    = 0, V iz = 0,     V₂|_z    = V 2"

^l' Z N +2                ^{1 I Z} N +2                 ² Z N +2        ⁰²

Пусть на подвижной границе сопряжения подобластей Z нет никаких источников и стоков массы. Тогда должно выполняться условие непрерывности потоков:

⁽ V i ^{+ и )}1 Zn + 1 -0 = u -Z „ + 1 +0

С учетом (3) граничные условия для напряжений па границе z = Z_N^_X приобретают следующий вид:

^ N +1 ⁽ u 1,2 ⁺ u 2,1 )      =   ^ | ^р 1 Z , ,1 ⁺ ^ ^(р k   ^Р к -1 ) Z k ,1 | ⁽ Z i   ^Zi +1 ) ,

Z N ^{+ 1}        i =1 V            к =2                       7

N

^- P ⁺ 2 Ц n +1 u 2,2k =^- Е р i ( Zi ^- Z +1 ) .

Z N +1          i =1

3.    Численная модель

Численное решение общей системы уравнений находилось следующим образом. По положению поверхности и границ слоев в начальный момент времени вычислялось поле скоростей в нижней подобласти D. . Для решения краевой задачи (7)-(13) применялся модифицированный метод конечных элементов в сочетании с методом проекции. Затем, по известным значениям скоростей на границе сопряжения Z_v2 вычислялось поле скоростей в верхней подобласти D_x . После этого устанавливались положения границ слоев на следующем временном слое путем численного решения системы параболических уравнений (6). Далее повторялась вся процедура (подробное описание численного алгоритма приводится в работе [9]).

При построении численной модели течения многофазной вязкой жидкости основной проблемой является сопряжение разнородных уравнений. Как показано в [9], при использовании в постановке задачи естественных условий непрерывности поля скоростей и напряжений на границе сопряжения разнородных сред на больших временах поле скоростей определяется с большой погрешностью даже при задании малого шага дискретизации по времени. С целью поиска путей повышения точности решения и сокращения времени счета проведено асимптотическое исследование уравнений Рейнольдса в подобласти D j и получено уравнение, связывающее профили границ слоев на больших временах со скоростями на границе сопряжения Z_{N +1}, которое не зависит от начального положения границ Z :

N +1           Л

Р 1 A 1 Z 1,1 + Е A ik р k Z k ,1 1 + ( u + V 1 ) Z N ,_и + ( u 2 + V 2 ) = 0.

k =2               у ,1

В настоящей работе асимптотическое уравнение (16) использовалось в качестве дополнительного условия при решении системы разнородных уравнений (1)-(15). Численное решение тестовых задач (см. [5]) показало, что применение (16) в качестве дополнительного ограничения на искомое решение позволяет существенно сократить вычислительные затраты, по сравнению с ранее разработанными вариантами моделей [11].

4.    Исследование эволюции течения для варианта с трехслойным пластом

В модельной задаче верхняя подобласть D_x разделялась на 3 слоя: осадочный чехол с плотностью 2500 кг/м ³ и вязкостью 10 ¹⁶ Па ■ с, гранитный слой с плотностью 2700 кг/м ³ и вязкостью 10 ²¹ Па ■ с, базальтовый слой с плотностью 3000 кг/м ³ и вязкостью 0,5 ■Ю²¹ Па ■ с и тонкий (в начальный момент времени) слой с плотностью 3100 кг/м ³ и вязкостью 10 ¹⁷ Па ■ с, в котором аккумулировался легкий компонент. Среда, заполняющая нижнюю подобласть D ₂, имела следующие параметры: плотность тяжелого компонента 3300 кг/см ³ и вязкость 10 ²² Па ■ с, плотность легкого компонента 3100 кг/м ³ и вязкость 10 ¹⁷ Па ■ с . Вертикальный размер расчетной области составлял L = 400 ■Ю³ м . В начальный момент времени объемная концентрация легкого компонента задавалась равной 0,01; в процессе эволюции течения ее вариации оказались пренебрежимо малыми. Поток легкого компонента на нижней границе расчетной области имел профиль синусоидального вида:

V₀₂ =- cos ( ^ /( 2 n L ) ) .

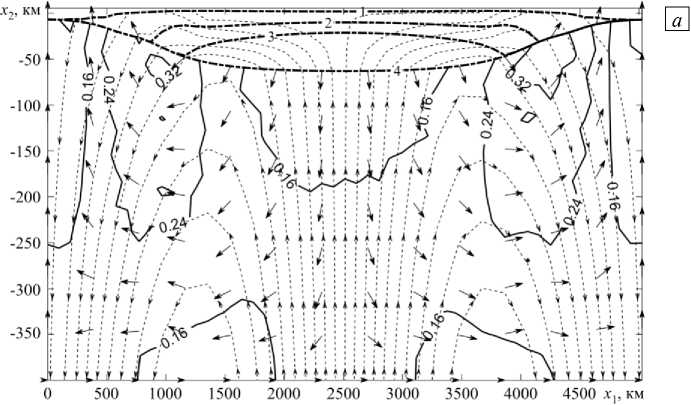
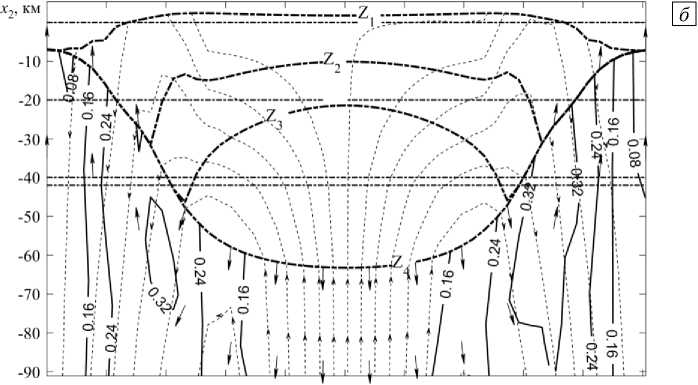
Произведен расчет эволюции течения в расчетной области. На рисунке 2 а приведены графики эволюции границ слоев в точке ^ = n L , а на рисунке 2 б — графики поля скоростей и профили дневной поверхности и границы между осадочным чехлом и гранитным слоем через ~30 (млн лет). Как видно, в центральной

О 500    1000   1500   2000   2500   3000   3500   4000   4500 л^км

Рис. 2. Поле скоростей в варианте с двухслойным пластом для момента времени около 30 млн лет: во всей расчетной области ( а ); в ее верхней части в увеличенном масштабе ( б ) (в начальный момент времени границы слоев задавались горизонтальными); сплошные линии - модуль скорости тяжелой фазы, пунктирные линии со стрелками - линии тока легкой фазы, стрелки - направления потока легкой фазы, пунктирные линии - дневная поверхность и границы раздела пласта, толстые штрихпунктирные линии - границы раздела земной коры (их начальное положение показано тонкими штрихпунктирными линиями)

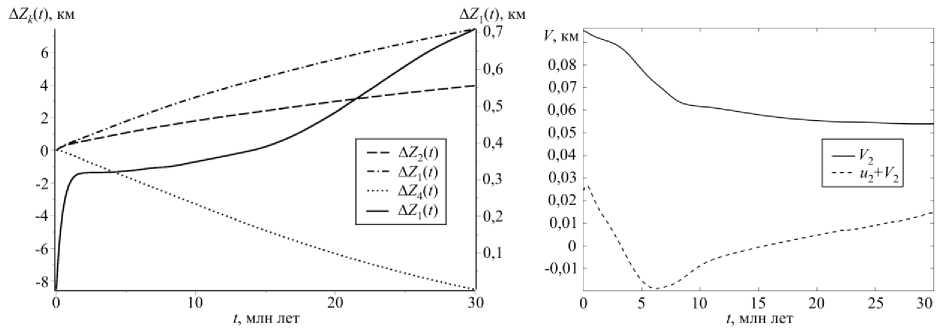
Рис. 3. Смещение A Z границ слоев верхней подобласти в центральной точке

Рис. 4. Эволюция V2 и u2 + V2  в центральной точке на границе сопряжения подобластей

части рисунков над восходящим потоком легкого компонента происходит его аккумуляция в нижнем слое подобласти D . Это приводит к тому, что верхняя и нижняя границы этого слоя начинают двигаться в противоположных направлениях. В области восходящего потока легкого компонента границы двух первых слоев поднимаются, и, соответственно, в области нисходящего потока легкого компонента они опускаются. В процессе эволюции область подъема этих границ расширяется в горизонтальном направлении, а скорость их подъема в центре уменьшается. В центральной части нижней подобласти D легкий компонент устремляется вверх, тяжелый компонент движется вниз, а на периферии перемещения обоих компонентов меняются на противоположные. Таким образом, скорости тяжелого и легкого компонентов везде получаются разнонаправленными.

На рисунках. 3, 4 представлена эволюция смещения границ слоев верхней подобласти A Z_z и вертикальной составляющей потока легкого компонент на границе сопряжения подобластей. Так как смещение поверхности много меньше, чем смещения границ раздела слоев, его значения приводятся на оси справа. Как видно из графиков, можно выделить два режима эволюции: быструю — на малых временах, и медленно изменяющуюся (квазистационарную) — на больших временах.

5.    Геофизические приложения

В качестве геофизического приложения осуществлен численный расчет аккумуляции области разуплотненной мантии под земной корой в Западно-Тихоокеанской зоне перехода океан–континент [12]. Эта зона характеризуется тепловым потоком высокой плотности, наличием разуплотненных астеносферных линз, а также погружающихся в сторону континента сейсмофокальных зон (очагов мантийных землетрясений), распространяющихся до глубин порядка 800 км.

В последние годы разработан ряд моделей и на их основе проведены исследования этих зон. Так, в [7, 13] моделируется процесс взаимодействия легкой горячей мантийной неоднородности (плюма) с литосферой и последующим формированием зон субдукции. Моделирование проводилось с учетом как глубинных, так и поверхностных факторов (денудации, осадконакопления). Для этой цели использовались однофазные модели со сложной реологией. Однако в этих работах легкая мантийная неоднородность считается существующей уже в самом начале процесса. В рамках однофазных моделей предполагается, что легкая неоднородность — это последствие диапиризма (возникновения и роста куполообразного возмущения за счет релей– тейлоровской неустойчивости с его последующим отрывом и всплыванием). Другим возможным путем образования такой легкой неоднородности является седиментационная конвекция. В [6] рассматривается процесс наращивания земной коры в результате адвекции легких дифференциатов, приводятся некоторые количественные оценки этого процесса, но его моделирование не реализовано.

При вычислениях верхняя подобласть расчетной области D была разделена на 5 слоев, что находится в соответствии с реальной структурой, включающей: осадочный чехол с плотностью 2500 кг/м ³ и вязкостью 1016 Па ■ с ; гранитный слой с плотностью 2700 кг/м ³ и вязкостью 10 ²¹ Па ■ с ; базальтовый слой с плотностью 3000 кг/м ³ и вязкостью 0,5 ■ I0 ²¹ Па ■ с ; тонкий (в начальный момент времени) слой разуплотненной мантии с плотностью 3100 кг/м ³ и вязкостью 10 ¹⁷ Па ■ с, в котором происходит аккумуляция легкого компонента. Среда, заполняющая нижнюю подобласть D , имела следующие параметры: плотность тяжелого компонента 3300 кг/см ³ и вязкость 10 ²² Па ■ с ; плотность легкого компонента 3100 кг/м ³ и вязкость 10 ¹⁷ Па ■ с . Вертикальный размер расчетной области составлял L - 400 ■Ю³ м. Вязкость считалась убывающей с глубиной по экспоненциальному закону [7, 14]: п = П о exp ( - 5 X 2/ L ) ■

В начальный момент времени объемная концентрация флюида задавалась постоянной, а в процессе эволюции течения имела пренебрежимо малые вариации.

В модели также учитывались поверхностные процессы — эрозия, денудация и осадконакопление, которые, по мнению многих исследователей, оказывают существенное влияние на структурообразование в верхних слоях литосферы [13, 15]. Для этого в правую часть уравнения (6) для дневной поверхности Z вводились дополнительные слагаемые:

(V      N^

Z1, t = || 41 Z1,1 + ^ Aik (pk -p k-1 ) Zk ,1 |-( u1 + V1 )z_z  (Zi - ZN+1 )l + (u 2 + V2 )z_z + Vden +

I                                                         I                   z = Z N +1                       I                       ^lz = Z N +1

W         k=2                   7

где   V_de „-(p Z j J — скорость осадконакопления, в — коэффициент интенсивности денудации,

V 1 ^-af— - 1 ] exp f ^- z— z ² ) 7 ^{1 + z} 22,1

Ip 1    7 I H 7

скорость эрозии на границе между осадочным чехлом и гранитным слоем, а — коэффициент интенсивности эрозии, H* — параметр, характеризующий скорость убывания эрозии с глубиной. Тогда для границы z в уравнение (6) необходимо добавить дополнительное слагаемое:

Z 1, t =

N

A 21 Z 1,1 ⁺ ^ Ai k ^(р к ^{— Р} к -1 ) ^Zk ,1 к =3

- (u + V1 )|

^z = Z N +1

(Z2 —ZN+1 )| + (u2 + V2 )|z_z  + V z=ZN+1

Л 1

[ z     z.> ।

--1^*2 I V^{1 + z} 2,1 .

Поток легкого компонента на нижней границе расчетной области задавался в виде куполообразного профиля:

V 02 = exP ( ^- ( ^ 1

—

П

n)2)—-J exp(—x 2) n 0

dx .

Согласно результатам геофизических наблюдений, любая эволюция плотностных неоднородностей (создание различных форм рельефа) идет всегда при их полной изостатической уравновешенности в региональном масштабе. Поэтому предполагалось, что в начальный момент времени земная кора находилась в состоянии изостазии, и впадина Охотского моря отсутствовала.

Произведен расчет эволюции течения с большими деформациями границ. На рисунке 5 приводятся поле скоростей и профили дневной поверхности, а также положение границы между осадочным чехлом и гранитным слоем примерно через 30 млн лет. По результатам моделирования можно заключить, что эволюция исследуемого процесса происходит следующим образом:

• –    в литосфере под подошвой коры в результате адвекции аккумулируется легкий компонент — разуплотненная линза, вертикальный размер которой со временем растет, а горизонтальный размер, наоборот, сокращается;

• –    линза локализуется под океанической корой;

• –    при увеличении размеров линзы дневная поверхность и границы раздела коры, расположенные выше, поднимаются;

• –    далее, при продолжающемся росте величины линзы, дневная поверхность постепенно опускается с образованием крупномасштабной впадины, глубину которой значительно увеличивают процессы эрозии, денудации и другие (финальная стадия эволюции представлена на рисунке 4).

  

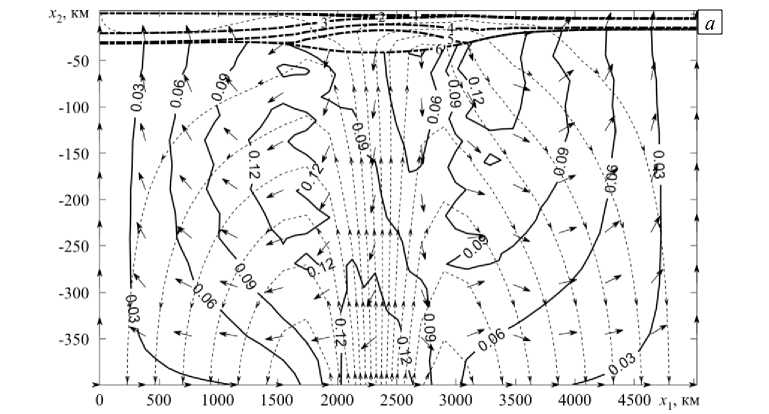
  Рис. 5. Поля скоростей в момент времени около 30 млн лет в литосфере переходной зоны океан–континент: во всей расчетной области ( а ); в ее верхней части в увеличенном масштабе ( б ); сплошные линии – модули скорости тяжелой фазы; пунктирные линии со стрелками – линии тока легкой фазы; стрелки – направления потока легкой фазы; пунктирные линии – дневная поверхность и границы раздела земной коры; толстые штрихпунктирные линии – границы раздела земной коры (их начальному положению отвечают тонкие штрихпунктирные линии); цифрами обозначены: дневная поверхность (линия 1 ), границы между осадочным чехлом и гранитным слоем ( 2 ), между гранитным и базальтовым слоями ( 3 ), между верхним и нижним базальтовыми слоями ( 4 ), между нижним базальтовым слоем и мантийной неоднородностью ( 5 ), между неоднородностью и верхней мантией ( 6 )

  
  
  

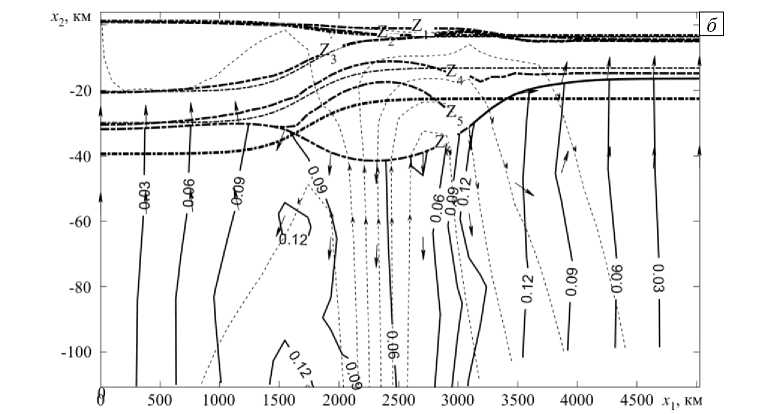
  Рис. 5. Продолжение

  
  

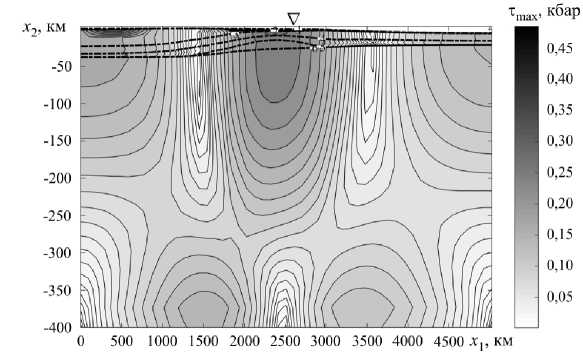
На рисунке 6 приведено поле максимальных скалывающих напряжений т_тах в модельной среде и один из вертикальных разрезов сейсмофокальной зоны Камчатки, взятый из [16]. Сопоставление результатов показывает, что положение большинства очагов сильных землетрясений попадает в зону возможных разрушений геоматериалов: 0, 3 ≤ τ ≤ 0, 5 кбар. Следует отметить наличие и другой зоны повышенных значений т_тах — слева под континентом. Геофизическими наблюдениями здесь также зафиксировано скопление очагов землетрясений.

а

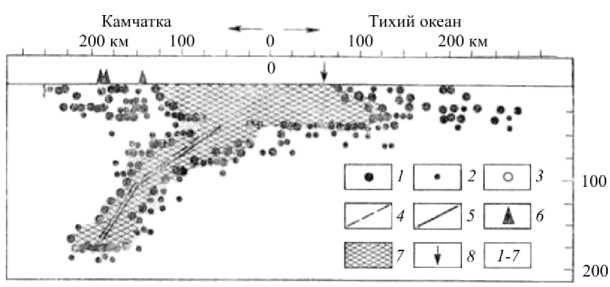
Рис. 6. Поле максимальных скалывающих напряжений в литосфере зоны перехода океан-континент во всей расчетной области через ~30 млн лет ( а ): треугольником на поверхности показано расположение формирующегося желоба; вертикальный разрез сеймофокальной зоны Камчатки [16] ( б), где цифрами обозначено: 1 - землетрясения с K >  9,5

( K - показатель согласно энергетической классификации землетрясений по шкале С. А. Федотова [16]); 2 - землетрясения с 7,5 < K <  9,4; 3 - землетрясения, координаты которых взяты из других бюллетеней; 4 - мода распределения числа землетрясений на данной глубине; 5 - медиана распределения числа землетрясений на данной глубине; 6 - вулканы; 7 - сейсмофокальная зона; 8 - проекция оси желоба

Как и расчет для модельной среды с трехслойным пластом, представленный в разделе 4, численное моделирование процесса аккумуляции разуплотненной мантии под земной корой в Западно-Тихоокеанской зоне перехода океан–континент показывает, что существование различных стадий эволюции течения с характерными масштабами времени, которые определяются не внешними факторами, а геометрическими и физическими параметрами самой исследуемой среды.

6.    Заключение

Разработана комплексная численная модель медленного течения многофазной жидкости в области, состоящей из относительно толстого слоя двухфазной жидкости и многослойного вязкого пласта на его поверхности. С помощью этой модели проведены вычислительные эксперименты для исследования многофазного течения вязкой жидкости. Полученные результаты показали, что эволюция течения состоит, по крайней мере, из двух стадий с характерными масштабами времени, которые определяются геометрическими и физическими параметрами изучаемой среды (в приложении к геофизике — геосферы), а не внешними факторами. Поля скорости тяжелого и легкого компонентов получаются разно направленными.

В качестве геофизических приложений, произведено численное моделирование процесса аккумуляции разуплотненной мантии под земной корой в зоне активного перехода океан–континент. Расчеты осуществлены с учетом более подробной структуры многослойного пласта и дополнительных процессов эрозии, денудации и осадконакопления. Особенности аккумуляции легкой мантии в недрах активных океанических окраин и распределения максимальных скалывающих напряжений, известные из других источников и найденные из численных расчетов в разделе 5, подтверждаются данными геофизических наблюдений [7].

Модель, разработанная автором статьи, и количественная информация, полученная на ее основе, могут быть полезными для более детального и всестороннего изучения структуры и глубинных движений в регионах с активными переходными зонами.

Работа выполнена по госбюджетной тематике ТОИ ДВО РАН «Математическое моделирование и анализ динамических процессов в океане» (Госрегистрация № 117030110034-7).