Комплексная форма дискретных отображений томсоновских автоколебательных систем

Современная нелинейная динамика [1] рассматривает эволюцию динамических систем как в непрерывном (НВ), так и дискретном времени (ДВ). При этом в области дискретного времени нелинейная динамика смыкается с цифровой обработкой сигналов [2] и объекты ДВ-динамики могут служить основой алгоритмов обработки. Для выполнения этих функций необходим широкий круг ДВ-систем, обеспечивающий возможность выбора заданной характеристики преобразования сигналов. Поиск таких систем следует рассматривать в качестве одной из задач нелинейной динамики в дискретном времени.

Как правило, объекты НВ-динамики являются результатом математической формализации физических (химических, биологических и т. д.) моделей реально существующих систем, в то время как ДВ-системы в большинстве случаев возникают в результате дискретизации времени в НВ-системах. Полученное таким образом разностное уравнение, следуя терминологии теории колебаний, можно обозначать как уравнение движения ДВ-системы, а как объект ДВ-динамики – дискретное отображение соответствующей НВ-системы. При этом способ дискретизации существенным образом влияет на форму дискретного отображения.

Широко известен ряд способов построения дискретных отображений. В качественной теории динамических систем – это сечения Пуан- каре [1]. Для гамильтоновых систем с помощью введения в гамильтониан нелинейных дельтавоздействий строятся универсальное и стандартное отображения [3]. Рассматривается также и самый прямой способ дискретизации времени – конечно-разностная аппроксимация производных в дифференциальном уравнении движения системы. Но он не дает эффективных алгоритмов преобразований сигналов ДВ-системами [2].

В настоящей работе для построения дискретных отображений аналоговых автоколебательных систем (АКС) томсоновского типа использован метод структурного синтеза в сочетании с принципом сохранения временного отклика линейных резонаторов при переходе к дискретному времени.

1.    Структурный синтез АКС

В качестве основного прототипа в непрерывном времени выберем осциллятор с уравнением движения вида d2 y to dy dy

+ 70 77 ^{+ ю} о У ^{= to} ° ^Y G ( У )77, ⁽¹⁾

dt2 Q dt dt где tog и Q — собственная частота и добротность резонансного контура АКС; у - параметр цепи обратной связи с нелинейностью усилителя G(y) – четной функцией входного сигнала. Формально при выполнении условий Q >> 1, у << 1 АКС (1) относится к классу томсоновских. При G(у) = 1 - у2 — это осциллятор Ван дер Поля.

Используемый способ проектирования ДВ-осциллятора в определенном смысле можно назвать структурным, поскольку он опирается на представление о структурной схеме томсоновской АКС (1), как кольцевом соединении блоков «резонатор – нелинейный усилитель – обратная связь».

Динамическую (инерционную) часть АКС (1) представляет резонансный контур с дифференциальным уравнением движения dry + Г0 dy + ®0 у = ®2 x (t),                  (2)

dt2 Q dt где x(t) – сигнал возбуждения. Контур (2) имеет импульсную характеристику

h ( t ) = to₀ exp

^- 2^ 0 t J ^{sin( to} o t ) •

Ее дискретные временные отсчеты, взятые с интервалом А, определяют импульсную характеристику ДВ-резонатора:

h [ n ] = А ■ h ( t n ) = 2nQ o a ⁿ sin ( 2 kQq n ) . (3) Здесь Qq = to o А /2п — собственная частота контура, измеряемая в единицах частоты дискретизации to d = 2п / А; a = exp ( -nQ o / Q ) — параметр диссипации.

Так как частотная характеристика ДВ-системы связана с ее импульсной характеристикой дискретным во времени преобразованием Фурье [2]:

H(jQ) = £ h[n] exp (-j2nQn), n=0

то для (3), проведя вычисления, получим

H ( j Q) = H ₊ ( j Q) + H - ( j Q) =

= j^_________ ₊          (4)

1 - a exp ( j 2nQ o ) exp ( - j 2nQ )

₊___________ j nQo___________

1 - a exp ( - j 2nQ o ) exp ( - j 2nQ )

Частотная характеристика (4) соответствует системе разностных уравнений движения вида y [ n ] = y + [ n ] + y -[ n ], y + [n] = aZoy + [n - 1] - jnQox[n],                 (5)

y-[n] = aZOy-[n - 1] + jnQox[n], где Zo = exp (j2nQo ) — множитель поворота. Отметим, что при действительном сигнале x[n] осцилляции y- [n] комплексно сопряжены по отношению к y + [n]: y- [n] = y + [n].

В автоколебательной системе с уравнением движения (1) роль сигнала возбуждения x ( t ) играет сигнал на выходе нелинейного усилителя, вход которого через обратную связь взаимодействует с выходом контура y ( t ):

x ( t ) = -^- G ( y ( t ) ) y ( t ).                         (6)

2nQ o

В этой записи введено обозначение для производной по безразмерному времени: y = А dy / dt .

С учетом связи (6) система разностных уравнений движения (5) для томсоновского ДВ-осциллятора принимает вид y [ n ] = y + [ n ] + y - [ n ], y + [ n] = aZo y + [ n - 1] - j 2 G (y [ n ]) y[ n ], y-[n] = aZOy-[n - 1] + j Y F (y[n]) y[n].

Сумма второго и третьего уравнений этой системы с учетом первого дает важное соотношение y [ n ] = aZo y + [ n - 1] + aZO y + [ n - 1] , указывающее на зависимость значения осциллирующей переменной y[n] в текущий момент дискретного времени n от значения переменной y + [n - 1], взятого в предыдущий момент n - 1. Такая временная зависимость позволяет построить ДВ-осциллятор в форме итерируемого дискретного отображения вида y + [n] = aZoy + [n - 1] - j 2 G (y[n]) y[n] ,(7)

где

y[n] = 2a Re (Zoy + [n - 1]) .(8)

При этом для связи отсчетов y [ n ] и y [ n ] предлагается использовать выражение вида [4]

sinc (2n Qo) 'y[n] = cos (2n Qo) y[n] - y[n - 1].(9)

Оно является точным для дискретных гармонических колебаний с частотой Qo. Как прибли- женное, предлагается распространить его и на квазигармонические автоколебания. С учетом (9) отображение (7) принимает вид y [ n ] = a Zo y + [ n - 1] + aZq y + [ n - 1], nQn y + [ n] = aZo y +[ n - 1] - j Y      0— x sin (2n Qq )

x G ( y [ n ] ) ( cos ( 2n Q o ) y [ n ] - y [ n -1] ) ,

Сформированное таким образом нелинейное разностное уравнение (10) представляет собой комплексную форму дискретного отображения (уравнения движения) томсоновской АКС.

2.    Метод MMA для ДВ-АКС

Отображение (10) воспроизводит в дискретном времени основные характеристики томсоновской АКС (1). Это нетрудно показать цифровым анализом генерируемых по алгоритму (10) времен- ных рядов, но мы воспользуемся здесь широко распространенным в теории нелинейных колебаний методом медленно меняющихся амплитуд (методом ММА) [5]. На ДВ-осцилляторы томсоновского типа метод ММА был распространен работах [6; 7]. Следуя им, генерируемый отображением (10) временной ряд (ДВ-автоколебания) представим в виде y + [ n ] = 2 A[ n ] Zn, где A[n] = a[n] exp ( jф[n]) — комплексная амплитуда автоколебаний; a[n] и ф[n] — действительные амплитуда и фаза. Тогда первое из уравнений (10) можно записать как y [ n]=a A [ n—1] Zn+a A * [ n—1] z- n,

Нелинейную функцию

F ( y ^{[ n ]} ) = G ( y ^{[ n} 1 ) ( cos ( 2 лПо ) y ^{[ n ] -} y ^{[ n - 1]} ) ⁽¹¹⁾

в правой части первого уравнения (10) в рамках метода ММА заменим первой гармоникой ряда Фурье:

F (y[ n 1) « 2 F (A [ n 1) Zn + 2 F (A [ n 1) Z- -n с комплексной амплитудой

F1 (A[n]) = j sin (2пПо )x x fG0 (a[n - 1]) - - G2 (a[n - 1])^ A[n - 1].

При этом использовано Фурье-разложение четной функции G ( y [ n ] )

G ( y [ n ] ) « G о ( a [ n ] ) +

^{+ - G} 2 ( a ^{[ n ]} ) ^exP ( j ²Ф^{[ n ]} ) Z 2 n ⁺

⁺ 2 ^G 2 ( a ^{[ n ]} ) exp (^- j ²Ф^{[ n ]} ) ^Z 0 ² n .

Отметим также, что в рамках используемой здесь методики ММА в нелинейности (11) считаем A [ n - 2] = A [ n - 1] и a = 1.

Используя в (10) представленные разложения и проведя очевидные математические преобра- зования, получим

A [ n ] = aA [ n -1] + медленный процесс изменения (с характерным временем релаксации Tr = Q / 2Qo) комплексной амплитуды A[n]. Пренебрегая этим воздействием, приходим к укороченному уравнению для комплексной амплитуды ДВ-автоколебаний

A [ n ] = a A [ n - 1] +

+ пП_оYI G 0 ( a [ n - 1] ) - - G ₂ ( a [ n - 1] ) I A [ n - 1].

Полученное разностное уравнение (13) сопоставим с укороченным уравнением для комплексной амплитуды автоколебаний в исходной аналоговой модели АКС (1). Нетрудно показать, что для автоколебаний вида

у ( t ) = 2 A ( t ) exP( j ® 0 1 ) + 2 A ( t ) exp(- j ® 0 1 )

уравнение движения (1) методом ММА сводится к дифференциальному укороченному уравнению dto

— A (t) =--0 A (t)

dt2

+ -2 0 ^Y ^ ^G о ( a ( t ) ) ^- 2 G 2 ( a ⁽ t ) ) 1 A ⁽ t ).

При переходе к безразмерному времени т = t А ¹ уравнение (14) принимает вид

— A (т) = -п ^°- A (т) + d т         Q

+ лП о Y f G о ( a (т) ) - ^- G 2 ( a (т) ) j A (т).

Учитывая разложение параметра диссипации высокодобротного контура в ряд по обратным степеням добротности

( _Ц)1 . -По a = exp -п ® 1 - п , f Q J Q приходим к выводу о том, что разностное укороченное уравнение ДВ-АКС (13) реализует алгоритм Эйлера для укороченного уравнения (15) аналоговой АКС. Таким образом подтверждается сделанное нами ранее утверждение о том, что отображение (10) воспроизводят в дискретном времени основные динамические характеристики томсоновской АКС (1).

+ nQ o Y | G о ( a [ n - 1] ) x A [ n - 1] +

-¹ g₂

( a [ n - 1] ) I x

3. Некоторые результаты анализа динамики ДВ-АКС

+ nQ o Y | G о ( a [ n - 1] )

-

1 _G

( a [ n - 1] ) I x

x A *[ n - 1] Z ₀ ^{2 n} .

Приведем ряд результатов, полученных для дискретного отображения осциллятора Ван дер Поля. В этом случае функция нелинейности

Последнее слагаемое здесь описывает высокочастотное воздействие (с периодом 7 = 1/ 2Q o ) на

F ( у ) = f^{1 -} 3 у ² j у ,

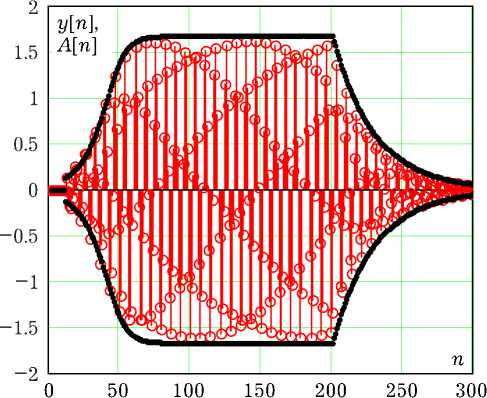
Рис. 1. Дискретные отсчеты мгновенных значений и амплитуды первой гармоники автоколебаний

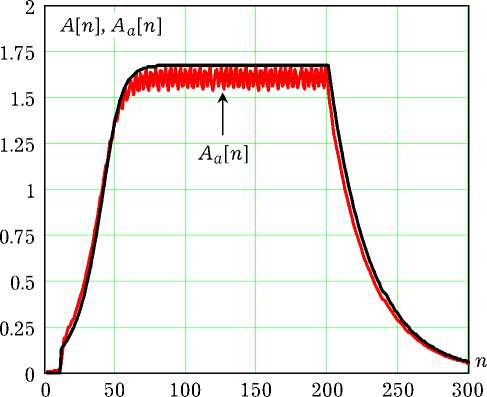
Рис. 2. Дискретные отсчеты амплитуды первой гармоники и огибающей автоколебаний

а отображение (10) и его укороченное уравнение

• (13)    принимают вид

y + [ n ] = a Z o y + [ n - 1] -

-

j Y e ( 1

-

У 2 [ n — 1] ) ( cos ( 2n Qo ) У [ n ] — y [ n — 1] ) ,

A [ n ] = a A [ n -1] + у e sin ( 2nQ o ) x

Yip i x|1 - a 2[ n - 1] IA [ n - 1].

I 4          J

Здесь в (16) для упрощения записи введен эффективный параметр обратной связи в ДВ-системе:

nQn

Y e = Y . z₉ " v sin ( 2n Qo )

На рис. 1 точками приведены отсчеты ДВ-автоколебаний y [ n ], генерируемых отображением (16) со значениями Qo = 0.14 и Q = 13. Обратная связь с параметром у = 0.143 включается на интервале времени 11 <  n < 200. Пунктирной линией на рисунке показан график временной зависимости амплитуды автоколебаний, рассчитанный по укороченному уравнению (17). Как видно из графиков, зависимость a [ n ] = A [ n ]| с хорошим приближением воспроизводит амплитуду автоколебаний.

На рис. 2 график a [ n ] приведен вместе с графиком временной зависимости огибающей A_a [ n ] ДВ-автоколебаний y [ n ], выделенной методом аналитического сигнала с использованием дискретного преобразования Гильберта [2]. Зависимость A_a [ n ] кроме медленной кусочно-монотонной компоненты содержит компоненту, осциллирующую с частотой 2 Qo . Она возникает из-за наличия третьей гармоники в спектре сигнала y [ n ]. Заметим, что осциллирующая компонен-

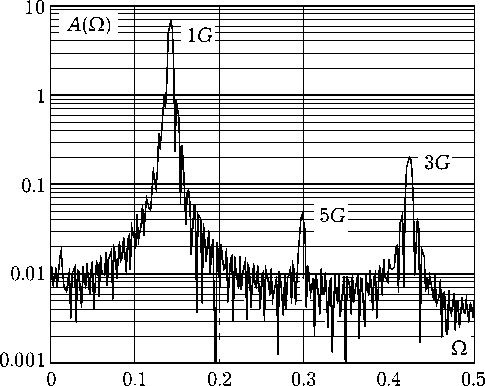
Рис. 3. Амплитудный спектр автоколебаний

та комплексной огибающей также содержится в решении амплитудного уравнения (12). Такое решение в теории нелинейных колебаний носит название улучшенного первого приближения [8].

Амплитудный спектр на рис. 3, где символами kG обозначены линии k -ых гармоник, рассчитанный для анализируемой реализации автоколебаний, демонстрирует неустранимый эффект подмены частот в нелинейных ДВ-системах. При определенных условиях он приводит к существенным особенностям в динамике ДВ–АКС [9; 10].

4.    Генерация хаоса дискретным отображением осциллятора Ван дер Поля

Ранее [11] отмечалось, что в ДВ-АКС, синтезированной по аналоговому прототипу – осциллятору Ван дер Поля, наблюдаются режимы хаотических автоколебаний. Они имеют место

3-2-10  1  2  3

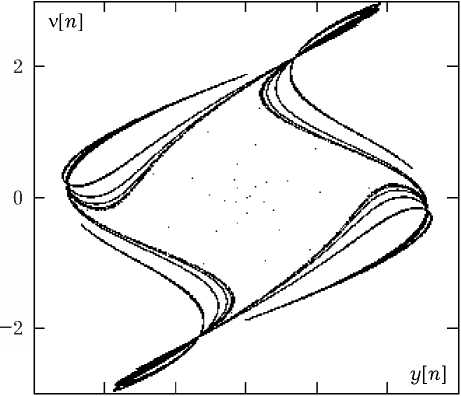
Рис. 5. Фазовый портрет хаотических автоколебаний

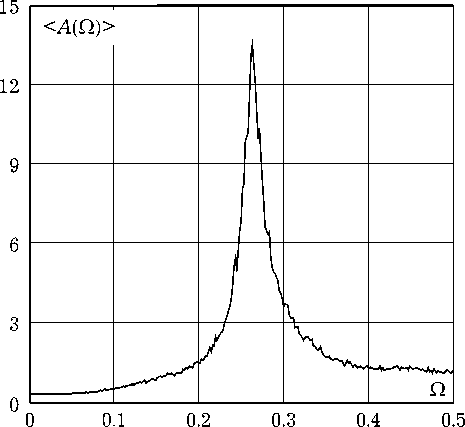
Рис. 4. Усредненный амплитудный спектр хаотических автоколебаний

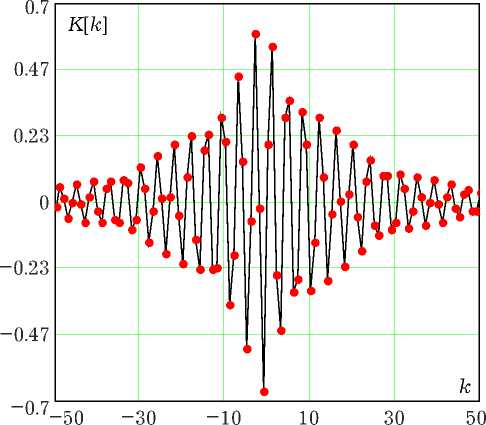
Рис. 6. Взаимная корреляционная функция компонент хаотических автоколебаний

и в дискретном отображении (16), модифицированным следующим образом:

y [ n ] = aZo y + [ n - 1] + а Z0 y + [ n - 1], у + [n] = аZoy + [n - 1] -                           (18)

• - j Y e ( 1 - y ²[ n - 1] ) ( p y [ n ] - y [ n - 1] ) ,

то есть введением параметра p вместо cos ( 2п Qo ) в формулу (9) для дискретной аппроксимации скорости y . При p = 1 отображение (18) эквивалентно уравнению движения ДВ-осциллятора Ван дер Поля из статьи [11].

На рис. 4 приведен усредненный амплитудный спектр автоколебаний, генерируемых отображением (18) с параметрами Qo = 0.22, Q = 13, Ye = 0.131 и p = 0.75. Уширенная спектральная линия является одним из эвристических признаков хаоса. Подтверждением хаотического ре- жима служит также имеющий ярко выраженную фрактальную структуру фазовый портрет дискретного отображения, представленный на рис. 5 в координатах (y[n], v[n] = y[n]).

Наряду с хаотическими автоколебаниями y [ n ] отображение генерирует и их компоненты Re ( y ₊ [ n ] ) и Im ( y ₊ [ n ] ) . Степень корреляции компонент иллюстрирует взаимная корреляционная функция K [ k ] = ^Re ( y ₊ [ n ] ) ■ Im ( y ₊ [ n + k ])}, показанная на рис. 6.

Заключение

Представленная здесь новая форма дискретных отображений томсоновских осцилляторов расширяют круг объектов нелинейной динамики в дискретном времени, имеющих свойства аналоговых автоколебательных систем. Практические применения предложенных отображений весьма разнообразны – моделирование сигналов и систем, нелинейная фильтрация дискретных (цифровых) сигналов, защита информации (в режимах генерации динамического хаоса).