Комплексная оценка несущей способности нахлесточных соединений в условиях вязкого и квазихрупкого разрушений

При изготовлении сварных конструкций для автомобилей особо большой грузоподъемности, горно-шахтного оборудования, строительно-дорожных машин и механизмов около 70 % всех сварных швов составляют угловые швы [1]. Оптимизация геометрических параметров сварных соединений с угловыми швами, ведущая к снижению объема наплавленного металла, возможна только на основе расчетной оценки несущей способности указанных соединений.

В данной работе рассматривается расчетная оценка несущей способности сварных нахлесточных соединений с лобовыми швами в условиях вязкого разрушения и их сопротивляемость квазихрупким и хрупким разрушениям с учетом локальных пластических деформаций в окрестности места сопряжения и величины радиуса последнего.

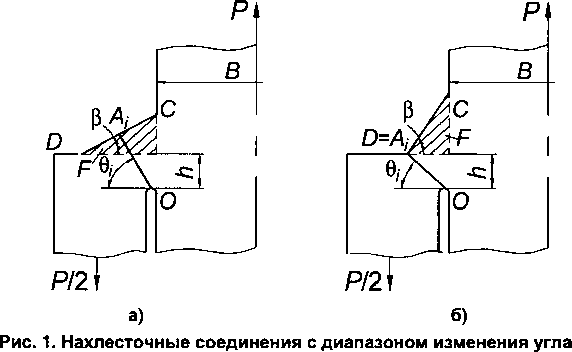
Теоретический анализ вязкой прочности нахлесточных соединений был выполнен с использованием полос скольжения по алгоритму кинематической теоремы предельного равновесия [2]. Согласно принятым расчетным схемам (рис. 1), линии скольжения О А, делят нахлесточные соединения с лобовыми швами на жесткие недеформируемые блоки.

Мощность внутренних w_L и внешних w_p сил на единицу длины соединения в плоскости, перпендикулярной чертежу (рис. 1), определяется выражениями [2]:

w_L=2kU_Ll_p, w_p=PU₀,                                                   (1)

где к - предел текучести материала при чистом сдвиге, к=<з_Т)4з - для неупрочняющихся материалов, к = о_в /Л - для упрочняющихся в процессе пластического деформирования материалов [2], (<з_т и а_в- соответственно предел текучести и прочности материала); 1_Р - размер поверхности разрушения О А, в плоскости чертежа, для нахлесточных соединений: I =(h + J2FtgP)— cosP— , h - глубина проплавления; Р - угол наклона образующей шва; F - площадь шва; Р - погонное предельное усилие; U_L - скорость перемещения материальных частиц при пластическом течении вдоль линий скольжения ОА„ U_L = 7/₀/sine, , U_o - средняя скорость деформирования.

Исходя из баланса мощности внутренних и внешних сил (w_L = Wp) получено выражение для оценки несущей способности (средних предельных напряжений сг_ср) для нахлесточных сварных соединений:

В 2 ,

"ср=- = ^--"₅-^-^р. (2) где V = 'J2F/в - относительная площадь наплавленного металла (В - толщина пластины); к^ - коэффициент, зависящий от геометрических параметров сварных соединений. В общем виде этот коэффициент может быть представлен в следующем виде:

^р=(п+75р)-

COsP sin (Р + О,) sin 6,

где т] = h/^lF - относительная глубина проплавления пластин.

Угол наклона плоскости вязкого разрушения 6, находим из условия минимума мощностей

6wL _ dwP

= 0.

В зависимости от сочетания геометрических параметров нахлесточные соединения имеют два диапазона изменения угла 6„ характеризующихся местоположением точки А, по отношению к вершине углового шва С (рис. 1, а, б).

В первом диапазоне (0<Р<Р*), где Р* - граничные значения углов Р, определяемые из уравнения — = tg—JtgP* , траектория вязкого разрушения, совпадающая с линией скольжения т] 2 v

ОА_Ъ распространяется от вершины непровара стенки (точки О) до наклонной поверхности углового шва CD (см. рис.1, а).

1 2 2

k$=2tg2 J-+ * 2(tgP

'tgP

Во втором диапазоне (Р*<Р<л/2) траектория вязкого разрушения распространяется от вершины непровара стенки (точки О) до точки перехода от шва к основному металлу присоединяемой пластины (нахлестки) A, = D (рис. 1, б):

®2

1,(2) кпР

= 'n + l/ntgP-

Анализ полученных выражений (2)-(5) открывает возможность оптимизировать геометрические параметры угловых швов при конструктивно технологическом проектировании рассматриваемого сварного соединения. Из условия Эо_ср/Эр = 0 были найдены соотношения, позволяющие по известной глубине проплавления h и площади наплавленного металла F (т. е. по известному значению параметра т| = A/V2F ) определить оптимальные углы наклона образующей шва Р = Р_опт, обеспечивающие максимальную несущую способность рассматриваемых сварных соединений:

l-2cos|3onT

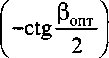
Зависимости оптимальных значений углов Ропт от относительной глубины проплавления Т| для нахлесточных соединений приведены на рис. 2. Как следует из выражения (6), для нахлесточных соединений, выполненных ручной дуговой сваркой без проплавления стенки, оптимальное значение угла Ропт = 60°. С увеличением относительной глубины проплавления т] нахлесточных соединений наблюдается уменьшение оптимальных значений Ропт (Ропт < 60°). Следует от метить, что оптимальные значения углов Ропт находятся в I диапазоне их изменения.

Оценку несущей способности нахлесточных сварных соединений в условиях квазихрупкого и хрупкого разрушения осуществляли, используя критерий обобщенного нормального разрыва [3], в следующей форме:

Т^ФкФхФплФр ’ где КХс - критическое значение коэффициента интенсивности, при котором произойдет разрушение; фк - поправочная функция; учитывающая конечность геометрических размеров; фх - поправочная функция; учитывающая совместное действие нормальных и сдвигающих напряжений в окрестности места сопряжения; фт - поправочная функция, учитывающая образование зон локальной текучести в окрестностях места сопряжения; фр- поправочная функция, учи-

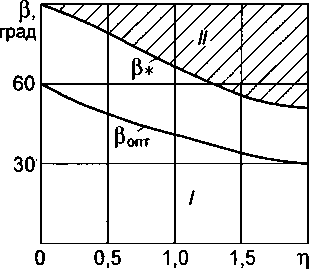
Рис. 2. Зависимость оптимальных значений углов |301ГГ от относительной глубины проплавления т] нахлесточного соединения. I, II - диапазоны изменения углов 0

тывающая конечность радиуса сопряжения.

Для определения поправочной функции фк, согласно работам [3, 4], рассматриваемые сварные соединения приводили к эквивалентной (с точки зрения идентичности напряженного состояния и характера локального разрушения в окрестности места сопряжения) пластине с наклонным трещиностойким концентратором напряжений. В результате теоретического анализа было полу чено следующее выражение: Гл z И где Фь Ф2 - параметрические функции; Ф; = 1 + 2\|/>/tgP tgy*, Ф2 = sin2Y*, Y* ~ уг°л наклона трещиноподобного концентратора в эквивалентной пластине (рис. 3).

В условиях нагружения смешанного типа напряженное состояние в окрестности вершины концентратора определяется коэффициентами интенсивности напряжений Кх и Ки, отношение которых Х = ^Кх/Кп^, согласно [3], описывается выражением: X = ctgy*.

Согласно работе [4], параметр X определяет направление страгивания трещины от места сопряжения (угол а,):

Х =

sin а,-

3cosa, -1

Для определения поправочной функции фх получено следующее выражение: cos а/2

(Ю)

Функция фпл, учитывающая локальную текучесть в окрестности вершины концентратора, с учетом особенностей, вносимых смешанным типом нагружения, равна [4]:

ФпЛ =

д/з,41Х2 + 2,06

cos а/2 (cos2 (а/2) -1,5Х sin а)

(П)

А

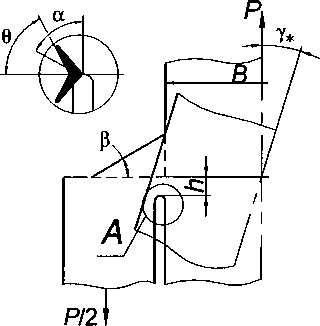
Рис. 3. Расчетная схема нахлесточного соединения с эквивалентной ей пластиной с наклонным трещиноподобным концентратом

Из сопоставления выражений (9) и (11) для нахлесточных соединений при практических инженерных расчетах удобнее пользоваться произведением поправочных функций фх и (р^ :

ФплФх =

Уз,41Х²+2,0б 1 + Х²

Дефекты типа непровара в нахлесточных соединениях имеют больший радиус в вершине, чем усталостная трещина. Оценивать несущую способность таких соединений следует с учетом радиуса в вершине непровара. Локальные разрушения соединения, согласно [4], происходят при условии достижения коэффициентом интенсивности напряжений значения А^_1с(р) = К_1с ^р₀/р, где

^ic(p) ~ критический коэффициент интенсивности напряжений с учетом радиуса концентратора р, р0 - эффективное значение радиуса концентратора.

Значение ро может быть приближенно определено по механическим свойствам материала [5]:

Ро =

0,08 Г К^ 2л Стр ,

Поправочная функция фр имеет вид [2]:

фр=Уро7р-

Используя приведенные соотношения для оценки поправочных функций фк- фх, ф™, фр, можно определить несущую способность сварных соединений с угловыми швами в условиях хрупкого (квазихрупкого) разрушения по известным конструктивно-геометрическим параметрам р, р, хр и р нахлесточных сварных соединений.

Расчет предельного состояния при квазихрупком разрушении сварных нахлесточных и тавровых [б] соединений с неполным проплавлением можно провести на основании комбинированного критерия, предложенного Е.М. Морозовым [7, 8] для соединений с предусмотренными трещиноподобными несплошностями, основанного на анализе энергетического состояния элемента с трещиной и полученного с использованием вариационного принципа:

где К^ - предел трещиностойкости материала, Qi - максимальное главное напряжение на линии трещины, q - показатель степени в выражении и* = ао^, устанавливающим связь между пере мещениями и* берегов трещины под действием ot за счет появления пластических зон в ее вершинах, а - коэффициент пропорциональности. Согласно экспериментальным данным работы [8] наиболее консервативное предельное соотношение между а и ^ при коэффициенте q = 1, то есть при линейной связи между пластическим перемещением и* и напряжением Стр

Для сварных нахлесточных соединений, склонных разрушаться как вязко, так и хрупко, оценка предельного сопротивления разрушению может быть получена по следующей зависимости:

ч Стер ) V ^1с У где о - напряжение, приложенное к сварному соединению при вязком разрушении, прочность сварного соединения при вязком разрушении, Ki - коэффициент интенсивности напряжений, Кк - критический коэффициент интенсивности напряжений, при котором реализуется хрупкое разрушение.

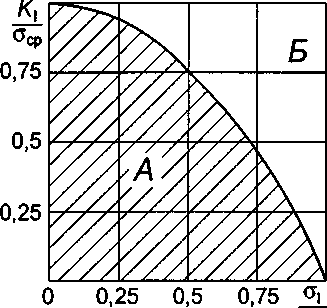
На рис. 4 приведена диаграмма предельного состояния при квазихрупком разрушении рассматриваемых нахлесточных сварных соединений, согласно формуле (16).

Выражение (16) устанавливает предельное соотношение между номинальными и локальными напряжениями при квазихрупком разрушении. Из анализа (16) и рис. 4 можно видеть, что использование комбинированного критерия для сварных соединений с предусмотренными трещинообразными несплошностями дает возможность расчетным путем определять по конструктивно-геометрическим параметрам соединений величину коэффициента интенсивности напряжений, при котором данное соединение при нагружении будет работать в области безопасного сочетания нагрузок и квазихрупкое разрушение не произойдет.

^Ф

Рис. 4. Диаграмма предельного состояния нахлесточного сварного соединения. В области А расположено безопасное сочетание нагрузок для данного сварного соединения, в области Б произойдет квазихрупкое разрушение