Комплексное преобразование радона распределений и аналитических функционалов

Статья посвящается авторами Ю.Ф. Коробейнику в честь его юбилея. В числе многих заслуг юбиляра авторы отмечают его большой вклад в сохранение традиций и высокого уровня исследований российской математической школы в это трудное для фундаментальной науки время.

Рассматриваются свойства комплексного преобразования Радона (ПР) распределений и аналитических функционалов. В терминах ПР распределений дано необходимое и достаточное условие представимости функций разностью логарифмических потенциалов. На основе свойств ПР целых функций, рассматриваемых как распределения, описан образ ПР сопряженного пространства к пространству целых функций многих переменных.

Преобразование Радона (ПР) является объектом исследования в течение достаточно длительного периода. Свойства ПР на пространствах распределений исследовались в работах [2, 4, 5, 8–11]. Следует отметить, что, в отличие от действительного случая, ПР распределений в комплексном пространстве мало изучено. В данной работе приводится ряд новых результатов, связанных с комплексным ПР распределений и его применениями. Основным результатом первой части работы является необходимое и достаточное условие представимости функций разностью логарифмических потенциалов. Данное условие формулируется в терминах ПР распределений. Этот результат принадлежит Секерину А. Б. Во второй части работы описан образ ПР сопряженного пространства к пространству целых функций многих переменных. Этот результат установлен Ломакиным Д. Е. (за исключением предложенного Секериным А. Б. определения ПР аналитического функционала).

Введем необходимые обозначения. Для z,w G C n полагаем hz,wi = 22 ZjWj • Единичная сфера в C ⁿ обозначается через S ^{2 n -1} , dσ — элемент площади сферы, dω 2 _n — стандартная мера Лебега в C n , А — оператор Лапласа. Если X — локально компактное пространство, являющееся счетным объединением компактов, то через C _c (X) будем обозначать пространство действительнозначных, непрерывных на X функций с компактным носителем. При этом будем считать, что на C c (X ) задана стандартная топология индуктивного предела. Далее, зарядом на X будем называть действительнозначный, непрерывный функционал на C c (X ). Известно [1], что любой заряд на X представляет

собой разность положительных борелевских мер, конечных на компактах. Через D(C n ) будем обозначать пространство гладких в C ⁿ функций с компактным носителем.

Классическое комплексное ПР функции ^ G D(C n ) задается равенством

[R^](s,^) = ^      [     ^(z) dX(z), (s,0 G C x (C n \ 0),            (1)

|4Г hz,e/ieii=s/iei где dX — элемент площади на гиперплоскости z : hz,£/|£|i = s/|^|.

Для любой функции ^ G D(C n ) и a G C \ 0 верно

^[Ry^](as,a<⁾ = ^{|a| -2 [R}y^](s,^⁾,                               ⁽²⁾

поэтому функцию [R^](s,£) мы будем отождествлять с ее сужением [R^](s,w) на C x S ^2n-1 . Если ^ G D(C ⁿ ), то [R^](s,w) G D(C x S ^2n-1 ), где через D(C x S ^2n-1 ) мы обозначаем пространство непрерывных по (s, w) функций ^(s, w), принадлежащих D(C) при каждом фиксированном w (будем считать, что на C x S ^2n-1 задана стандартная топология произведения).

Приведем определение ПР распределений, предложенное в [2, с. 171]. Рассмотрим векторное пространство M , образованное функциями вида d2n-2 [R^](s,w)

^(s,w)= dsn-idsn-1 ’ ^ G D(C )•

Пусть F G D 0 (C n ). На пространстве M определим функционал Lf :

(-1)n-1bnhLF ,^ = hF,^’(4)

где ^ и ^ связаны соотношением (3). Постоянная b n > 0 в (4) определяется таким образом, чтобы для регулярных распределений, задаваемых основными функциями, обобщенное ПР совпадало с обычным. В силу формулы обращения для ПР [2, c. 165] функционал L F определен корректно. Преобразованием Радона RF распределения F называется продолжение функционала L F на D(C x S ^2n-1 ). Данное продолжение всегда существует, но не обязательно является распределением на D(C x S ^2n-1 ). Кроме того, в силу неединственности продолжения, ПР распределений определено неоднозначно, что является одной из основных трудностей при исследовании его свойств. Другим неудобством является также то, что в определение ПР распределений необходимо включать пространство, на которое продолжается функционал L F . Это пространство, в свою очередь, зависит от рассматриваемой задачи.

Зададим на [0, го) x S ^2n-1 стандартную топологию произведения. Для множества A С C n обозначим через A множество точек (t, w) G [0, го) x S ^2n-1 , таких, что гиперплоскость z : hZ’W'i = t пересекает A. В [3, с. 11] доказано, что для открытого множества Q и компакта K в C n множества Q и K соответственно открытое и компактное подмножества в [0, го) x S ^2n-1 .

Пусть u(z) — плюрисубгармоническая функция в C n . Функция u(z) называется логарифмическим потенциалом, если на [0, го) x S ^2n-1 существует положительная мера ^, такая, что для любой области Q СС C n верно равенство

u(z) =

ln |t - hz,wi| d^(tHq(z),

—

Q где функция Hq(z) плюригармонична в Q. Мера ^ называется логарифмической мерой потенциала u(z).

Функция u(z) в C n называется разностью логарифмических потенциалов, если u(z) = u i (z) — U 2 (z), где u i (z), U 2 (z) — логарифмические потенциалы.

Задача представления функций разностью логарифмических потенциалов имеет самостоятельный интерес, а также важные приложения к вопросам построения мероморфных функций с заданным ростом и представления аналитических функций рядами экспонент [3]. В монографии [3] приведен ряд достаточных условий представимости функций разностью логарифмических потенциалов. Следующая теорема дает необходимое и достаточное условие.

Напомним, что действительнозначная функция u(z) называется 6-субгармонической, если она равна разности субгармонических функций [7].

Теорема 1. Пусть u(z) — д-субгармоническая функция в C n . Для того, чтобы u(z) была разностью логарифмических потенциалов, необходимо и достаточно, чтобы преобразование Радона распределения F = A n u имело нулевой порядок сингулярности, т. е. продолжалось до заряда на C х S ^{2n 1} .

C Необходимость. Пусть u(z) = u i (z) — U 2 (z), где u i (z), U 2 (z) — логарифмические потенциалы, а ^ i и ^ 2 — их логарифмические меры. Положим v = ^ 1 —^ 2 . Из определения логарифмического потенциала следует, что для любой области Q СС C n верно равенство

u(z) =

ln |t — hz,wi dv(t,w) + H q ( z ) ,

_

q где функция Hq(z) плюригармонична в Q.

Пусть ^(z) — любая функция из D(C ⁿ ). Имеем [3, с. 15]

j ln |s — hz, wi|A^(z) dw _{2 n} (z) = 2n[R^](s, w), (s,w) G C х S ^{2n i} .          (6)

C ⁿ

Тогда для любой области Q СС Cn, такой, что supp(^) СС Q, из (5) и (6) получаем hAnu, ^i = hu, An^i = 2n

/

£RA ^{n i} y] (t, w) dv(t,w).

— q

Легко показать, что из включения supp(^) СС Q следует, что носитель сужения на [0, го) х S2n-1 функции [RAn-iy] (s,w) содержится в Q. Поэтому верно hAnu, ^i = 2п

/

£RA ^{n i} y] (t, w) dv(t,w).

[0, ro ) x S ^2n-1

Из формул, связывающих ПР функции и ее производных [2, с. 162], следует

£RA ^n-i y] (s, w) = ^{d 2} n ^{2 [ R} ^ ^{]( s, w )} ,   (s, w) _G C х S ²ⁿ - ¹ .

l rj \     7        dsn—ids'n—i ’    \ ’ /

Поэтому из (7) следует, что для функционала LF , определяемого на пространстве M по распределению F = Anu равенством (4), верно hLF ,fi = (—1)n-ibn12n

[0i, x i x S ²ⁿ

j    ^(t,w) dv(t,w"),

ψ ∈ M.

Последнее равенство очевидно определяет непрерывное продолжение Lf на C c (C х S ^{2n 1} ). Необходимость доказана.

Достаточность. Пусть функционал Lf, определяемый по распределению F = Anu равенством (4), продолжается до заряда ^ на Cc(C х S2n-1). Для функции h(t,w) Е Cc([0, го) х S2n-1) определим ее продолжение на C х S2n-1 равенством he(s,w) = h(|s|,e-i6w), где s = 0, 9 = args. При этом очевидно he(s,w) Е Cc(C х S2n-1). Зададим на [0, го) х S2n-1 заряд v равенством j    h(t,w) dv(t, w) =

[0i, x i x S' ²ⁿ

—Ц bn    I h ^e (s,w) d^(s,w),

2n       J

C x S ^2n- 1

где число b n то же, что и в (4). В силу (2) для преобразования Радона [R^](s,w) любой функции ^(z) Е D(C ⁿ ) и любого 9 Е [0, 2п] верно [R^](s,w) = [R^](e i⁶ s^ ⁹ w). Поэтому

J    [R^](t, w) dv (t, w) =

|0i, x i x S ²ⁿ

(—Г-Ч

2п

■ j [R^](s,w) d^(s,w).

C x S ^2n-1

Представим заряд ν разностью положительных мер ν 1 и ν 2 и, используя явный вид формулы построения логарифмического потенциала по заданной мере [3, с. 54], построим логарифмические потенциалы u i (z) и U 2 (z) такие, что v i и V 2 — соответственно, их логарифмические меры. Пусть u(z) = u 1 (z) — u ₂ (z) и ^(z) — любая функция из D(C ⁿ ). Из определения логарифмического потенциала и из (6) следует

(A ⁿ (u i — U 2 ),^i = Ч

—

U 2 , A n ^i = 2n

/

£RA ⁿ 1 y] (t,w) dv (t,w).

[0, x i x S ²ⁿ

Тогда из (8) получаем hAn(ui — U2)4 = (—1)n-1bn

I   £RA ^{n 1} y] (s,w) d^(s,w).

C x S ^2n-1

Так как в обозначениях формулы (4) мера ^ задает функционал Lf, где F = Anu, то hAn(ui — u2)4 = (Anu,4

Поскольку здесь y(z) — любая функция из D(C ⁿ ), то разность h(z) = u(z) — (u i (z)— U 2 (z)) удовлетворяет обобщенному уравнению A ⁿ h(z) = 0. В силу эллиптичности оператора A n функция h(z) почти всюду в C n равна некоторой гладкой функции H (z) [6, с. 81]. Далее [3, с. 64] любая гладкая функция в C ⁿ — разность логарифмических потенциалов. Таким образом, доказано существование логарифмических потенциалов v i (z) и V 2 (z), таких что почти всюду в C n верно u(z) = v i (z) — v ₂ (z)- Так как субгармонические функции, равные почти всюду, равны тождественно, то же самое верно и для δ -субгармонических функций. Тогда всюду в C n верно u(z) = v i (z) — v ₂ (z). B

Рассмотрим пространство H (Cn) целых в Cn функций в стандартной топологии равномерной сходимости на компактах. Через H0(Cn) будем обозначать пространство всех линейных непрерывных функционалов на пространстве H(Cn). Введем также пространство Hc(C х S2n-1) функций вида f (s, w), (s, w) Е C х S2n-1, непрерывных по совокупности переменных и целых по s в C. Топологию в Hc(C х S2n-1) зададим c помощью счетного набора норм kfkk =

max | s | 6 k,w e S ^2n- 1

If (s,w)| (k = 1, 2,...).

На пространстве C (C х S ^{2 п} 1 ), состоящем из функций, непрерывных на C х S ^{2 п 1}

рассмотрим оператор

[R * f](z)= /

_S 2 n - 1

f (hz,wi,w) da(w).

Этот оператор является дуальным к ПР, т. е. для любой функции у из D(C n ) верно [3,

c. 10]

j [R * f](z)y(z) d^ 2n (z)) =

C ⁿ

j   f (s, w)[Ry](s, w)dш ₂ (s) da(w).

C x S ^2n-1

Назовем преобразованием Радона функционала y G H'(Cn) линейный функционал, заданный на Hc(C х S2n-1), и определяемый соотношением hRy,Уi = hy, R*yi,

где у G H c ( C х S ^2n-1 ).

Теорема 2. Функционал Ry, задаваемый формулой (10) , непрерывен в топологии H c ( C х S ^{2 п -}1 ).

C Для доказательства теоремы достаточно показать, что для любой последовательности у k G H c ( C х S ^{2 n -}1 ), сходящейся к нулю в топологии H c ( C х S ^{2 n -}1 ), последовательность комплексных чисел hR µ, ϕ k i сходится к нулю.

Пусть {у к } С H c ( C х S ^2n-1 ) и у к ^ 0 в топологии H c ( C х S ^{2 n -}1 ). Нетрудно показать, что оператор R * непрерывно отображает пространство H c ( C х S ^2n-1 ) в H (C n ). Тогда последовательность R*yk ^ 0 в топологии H (C n ), а, следовательно, так как y G H ' (C n ), hy, R * ^ k i ^ 0. Из формулы (10) следует тогда, что hRy,y k ) ^ 0. B

Через H C (C х S ^2n-1 ) будем обозначать пространство линейных непрерывных функционалов на H c ( C х S ^2n-1 ). Из определения следует, что оператор ПР аналитических функционалов линеен на H ' (C n ), т. е., в силу теоремы 2, R : H ' (C n ) ^ H C (C х S ^2n-1 ) — линейный оператор.

Пусть Ker R * — ядро оператора R * , т. е.

Ker R * = {у G H c ( C х S ^{2 n -}1 ) : [R * y](z) = 0}.

Следующая теорема дает описание образа оператора R.

Теорема 3. Пусть f G H C (C х S ^{2 n -}1 ). Для того, чтобы функционал f был преобразованием Радона Ry некоторого функционала y G H ' (C n ) необходимо и достаточно, чтобы для произвольной функции у G Ker R * было выполнено условие:

h^f,yi = °.

C Докажем необходимость. Пусть y G H ' (C n ) и f = Ry. Тогда, по определению, для любой функции у из Ker R * имеем:

hf,yi = hRy, у) = hy, R * yi = 0.

Необходимость доказана. Докажем достаточность.

Пусть дан линейный непрерывный функционал f на пространстве H c ( C х S ^{2 n -}1 ). Пусть далее для любой функции у из Ker R * верно hf, у) = 0. Докажем, что найдется такой функционал y G H ' (C n ), что Ry = f .

Положим для ф Е H (C ⁿ )

<У,ф> = hf,yi, где y — любая функция из Hc(C х S2n-1) такая, что R*y = ф. Покажем, что функционал у определен корректно. Сначала покажем, что для любой функции ф Е H(Cn) существует такая функция y Е Hc(C х S2n-1), что R*y = ф. Рассмотрим оператор A : H(Cn) ^ Hc(C х S2n-1), задаваемый формулой

[AF ](s,w) =

n-1

ф П(Е z* д- +ji)

2ni     \       dz*/ j=1 \г=1/

F (z)

z = swj

где I — тождественный оператор. В силу теоремы Вейерштрасса о равномерной сходимости оператор A : H (C ⁿ ) ^ H c ( C х S ^2n-1 ) непрерывен. В [3, c. 75] показано, что если y = Аф, то для функции ф справедливо равенство ф = R * y. Таким образом, для любой функции ф Е H (C ⁿ ) существует функция y = Аф, y Е H (C х S ^2n-1 ) такая, что R * y = ф ^и hy,^i = h ^f , yi.

Пусть теперь для функции ф Е H (C ⁿ ) существуют функции y 1 ,y 2 Е H c (C х S ^2n-1 ) такие, что ф = R * y 1 и ф = R * y ₂ . Тогда R * (y 1 — y ₂ ) = 0, а, следовательно, y 1 — y ₂ Е Ker R * . Из условия теоремы следует hf, ^ 1 — y 2 i = 0, т. е. hf, уФ = hf, y ₂ i. Поэтому значение h µ, ψ i функционала µ определено корректно. Покажем, что функционал µ непрерывен в топологии H (C ⁿ ).

Пусть последовательность элементов ф к из H (C ⁿ ) сходится к нулю в топологии этого пространства. Тогда, в силу непрерывности оператора А, последовательность у к = Аф к сходится к нулю в топологии H c ( C х S ^2n-1 ). Следовательно, hy,ф k i = hf,У k i ^ 0 при k → ∞, т. е. µ — линейный непрерывный функционал.

Покажем, что Ry = f. Пусть у — любая функция из H c ( C х S ²" ф. По определению h^Ry,yi = hy, ^R * yi = ^hf,yi. B

Дадим описание ядра оператора R * . Рассмотрим произвольную функцию h(s,w) из пространства H c ( C х S ^2n-1 ). Нетрудно показать, что функция h(s,w) может быть представлена в виде

^ h(s,w) = ^2 c k (w)s k , k=0

где коэффициенты С к (w) непрерывны, и ряд сходится равномерно на компактах из C х S ^{2 n -1} . В данных обозначениях справедлива теорема.

Теорема 4. Для того, чтобы функция h(s,w) из пространства H c ( C х S ^2n-1 ) принадлежала ядру оператора R * необходимо и достаточно, чтобы для любой сферической гармоники Y m степени m и любого k >  m выполнялось

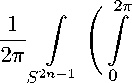
С к (w^⁶ )e i^k6

d9 Y m (w) da(w) = 0.

<1 Рассмотрим на D(C х S ^{2 n} 1 ) функционал F , задаваемый функцией h(s, w) Е H (C х S ^2n-1 ). Тогда для всех y(z) Е D(C ⁿ ), в силу формулы (9), имеем:

hF,Ryi = У

C x S ^2n-1

h(s, w)[Ry](s, w) dw ₂ (s) da(w) = У

[R * h](z)y(z) d^ 2n (z).

C ⁿ

Отсюда следует, что [R * h](z) = 0 тогда и только тогда, когда функционал F равен нулю на подпространстве RD(C х S ^{2 n -}1 ) q D(C х S ^{2 n -}1 ), образованном преобразованиями Радона функций из D(C n ). В [3, c. 79] доказано, что для того, чтобы функционал

G Е D'(C х S ^{2 n} 1 ) обращался в нуль на RD(C х S ^{2 п}

1 ) необходимо и достаточно, чтобы

для любой сферической гармоники Y m степени m >  1 функционал

2π hGYm,a(s)i = /f, 2П у a(sei6)Ym(wei6) d9V a(s) Е D(C)

задавался мерой P _m (s, s)dш 2 (s), где P _m (s, s) — многочлен степени не выше m — 1, а при m = 0 было G Y m = 0.

Согласно цитированной теореме, для произвольной функции a(s) из D(C) имеем:

2π hFYm ,a(s)i = ( h, 2П j a(sei6 )Ym(wei6) d9\

2π

C     _S 2 n - 1                 0

= j P m (s,s)a(s) dШ 2 (s),

C

a(se¹⁶)Y _m (we i⁶ )d9 j da(w) j dw ₂ (s)

где P _m (s, s) — многочлен степени не выше m — 1. По теореме Фубини имеем:

2π hFYm ’“fs'i = 2?/( /

0     _S 2 n - 1

[ h(s, w)a(se i⁶ )Y _m (we i⁶ ) dw ₂ (s) j da(w) j d9.

C

Положим во внутреннем интеграле s = Xe i⁶ . Тогда

2π hFYm '“Mi = 2?/( /

0      _S 2 n - 1

f h(Xe i⁶ ,w')a(X')Y _m (we¹⁶ ) dw ₂ (X) jda(w) jd9.

C

Меняя порядок интегрирования и полагая w = £e

-

^iθ , получаем

...-^

0 C _S 2 n - 1

h(Xe - i⁶ , ^e - i⁶ )a(X)Y m (e) da(^ ) j d^(X) j d9.

Пусть

2π

h(s,w) = — I hse i ,we⁸⁶ ) d9. 2n J

Тогда, вновь меняя порядок интегрирования, получаем

Г ( Г ~                   \                Г _ hFYm, a(s)i = /      / h(s, w)Ym(w)da(w) la(s)d^2(s)= /Pm(s,s)a(s) dw2(s).

Таким образом,

j h(s, w)Y m (w) da(w) = P m (s, s).

_S 2 n - 1

Так как функция h(s, w) представляется в виде

∞ h(s, w) = ^ck (w)s^k , k=0

то

2π

^ i r

h(s,w) = ^skY Ck (wei )

²ⁿ J

k=0

e ^ikθ dθ.

Следовательно,

2 π

C k (we i )e ^ik6 de\ Y m (w) da(w)\ s ^k = P m (s, s).

^{k =0}       _S 2 n - 1     0

Последнее равенство имеет место тогда и только тогда, когда для всех k >  m верно

1 2П

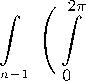
C k (we¹⁶ )e ^ike

d9 Y m (w) do(w) = 0. B