Комплексные решения на основе автоматически сменных модулей для реализации технологий лазерной обработки на станках с ЧПУ

Практика использования на производстве современных станков с ЧПУ показывает, что производственные мощности станков с ЧПУ используются лишь на 40–60 %. Часто производительность данных станков ниже, чем на универсальных станках особенно при малых партиях деталей [1]. Причина значительного снижения производительности станков с ЧПУ заключается в отсутствии нормативно-справочной литературы и методик проектирования циклов, удовлетворяющих требованиям современного автоматизированного производства. Используемые на отечественном производстве общемашиностроительные нормативы [2, 3] содержат в себе рекомендации по проектированию приближенного (стартового) цикла для диапазонов значений исходных параметров, заданных в виде интервалов диаметров и длин обрабатываемой поверхности, припусков, квали-тетов размеров заготовки и детали и др. Поэтому при проектировании операции для определенных условий необходимо производить адаптацию цикла к заданным исходным данным. Учиты- вая нелинейную взаимосвязь всех технологических факторов, невозможно быстро и просто подобрать параметры оптимального цикла, так как у технолога нет необходимого программного обеспечения. Отметим, что применяемые на производстве САПРы основываются также на общемашиностроительных нормативах 1990-х годов выпуска, которые не адаптированы под условия современного автоматизированного производства.

В настоящее время на производствах данную проблему решают двумя основными способами. Первым способом является покупка у производителей оборудования или инструмента узконаправленных рекомендаций по обработке детали для определенных условий. Данный способ является более дорогостоящим, и оттого менее используемым, и не может быть распространен на все машиностроительное производство. Поэтому данным путем могут воспользоваться только крупные предприятия, выпускающие большие партии однообразных изделий. Но чаще всего на отечественных предприятиях пользуются подбором режимов резания путем обработки ряда пробных заготовок. При этом на предприятии опираются на накопленный опыт обработки схожих деталей. Метод подбора режимов обработки является также достаточно затратным, так как требует дополнительных затрат на расходный материал (заготовки, инструмент и т. д.), время и производственные ресурсы. Отметим, что данный метод является неприемлемым для условий единичного и мелкосерийного производства, так как исходное количество заготовок изначально ограничено. В результате для гарантированного обеспечения качества обработки технолог в разы занижает режимные параметры цикла шлифования и тем самым снижает эффективность использования высокопроизводительных станков с ЧПУ.

Отметим, что вопросам теории проектирования оптимальных циклов обработки для станков с ЧПУ уделяется недостаточное внимание. Подавляющее число исследователей изучают частные стороны проблемы проектирования оптимальных управляющих траекторий [4–10]. Наибольшее внимание уделено моделированию силы резания и моделированию технологических ограничений (по точности, шероховатости, дефектному слою, износу и стойкости инструмента), влияющих на производительность операций. Итогом таких исследований являются частные рекомендации по режимам резания для лимитированного числа ограничений в узком диапазоне их варьирования. Очень мало представлено работ, направленных на развитие теории построения оптимальных управляющих программ для металлорежущих станков с ЧПУ, которые одновременно учитывают весь комплекс технологических ограничений (по параметрам заготовки, режущего инструмента, нестабильных условий организации производства и др.).

Решением проблемы отсутствия нормативно-справочной литературы, САПРов и методик является разработка методологии проектирования оптимальных ступенчатых циклов, удовлетворяющих требованиям современного производства. А также создание с помощью данной методологии нормативно-справочной базы и программного обеспечения.

Из-за наличия упругих перемещений в технологической системе и инерционности перемещающихся масс фактически снятый припуск не равен программной подаче. При ступенчатом переключении программной подачи значение фактически снятого припуска асимптотически приближается к программной подаче по экспоненциальному закону. На протяжении всего цикла текущее значение фактически снятого припуска ограничивается комплексом технологических ограничений, включающим в себя такие основные ограничения, как требуемая точность получаемого размера, шероховатость, микротвердость поверхности, стойкость режущего инструмента, мощность привода станка и др. (рис. 1). Для обеспечения максимальной производительности операции необходимо стремиться к тому, чтобы текущее значение фактически снятого припуска на протяжении всего пути снятия припуска максимально приближалась к области ограничений. В результате величина фактически снятого припуска будет максимально допустимой тем или иным ограничением, а цикл – производительней. Управление траекторией фактически снятого припуска осуществляется путем ступенчатого изменения программной подачи.

В основе методологии проектирования оптимальных циклов находится математическая модель процесса съема металла, которая отражает зависимость между программной подачей, величиной фактически снятого припуска и упругими деформациями технологической системы. Модель базирует на силовой модели процесса внутреннего шлифования, которая охватывает большую часть технологических факторов, влияющих на изменение силы резания (скорость вращения круга и заготовки, механические свойства шлифуемого металла, геометрические пара-

Расчет и конструирование

метры зоны контакта круга и заготовки, характеристика, степень затупления зерен круга и т. д.). На основании численных значений фактически снятого припуска можно рассчитать текущее значение диаметральных размеров обрабатываемой поверхности и их колебание на каждом ходе инструмента в разных сечениях по всей длине обработки. Текущее значение снятого припуска вычисляется путем суммирования значений фактически снятого припуска на каждом ходе инструмента. Более подробно с моделью процесса съема металла для внутреннего шлифования можно ознакомиться в следующих статьях [11–14].

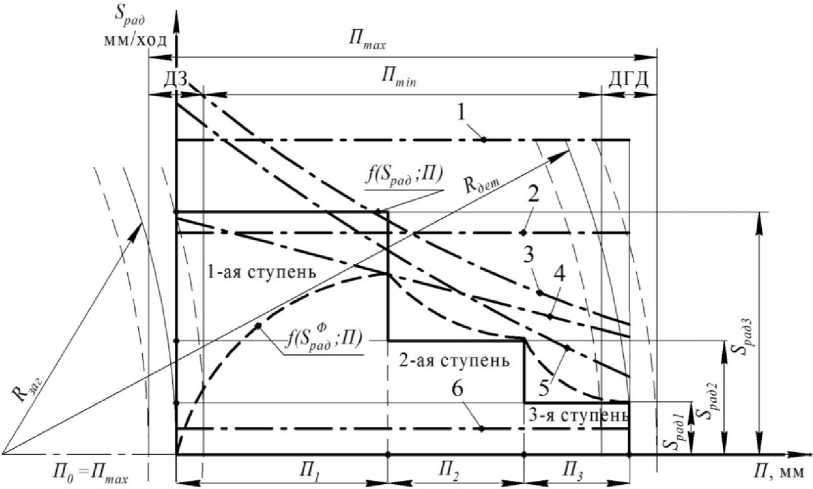
Рис. 1. Двухмерное представление 3-ступенчатого цикла внутреннего шлифования с наложением областей ограничений: 1 – ограничение по максимальной подаче станка; 2 – ограничение по осыпаемости круга; 3 – ограничение по прижогу; 4 – ограничение по точности размеров; 5 – ограничение по шероховатости; 6 – ограничение по минимальной подаче станка; ДЗ – допуск на заготовку; ДГД – допуск на готовую деталь; S^Ф рад – фактически снятый припуск, мм/ход; S рад – программное значение радиальной подачи, мм/ход; П – припуск, мм

Задача оптимизации цикла шлифования для обработки конкретной партии заготовок требует отыскания детерминированных режимных параметров цикла при нестабильных значениях ряда технологических ограничений и условий шлифования. Такая постановка задачи оптимизации является наиболее сложной и относится к области нелинейного программирования. Анализ методов дискретной оптимизации показал, что наиболее приемлемым для оптимизации циклов является метод динамического программирования (МДП) [15]. Применение МДП обусловлено тем, что данный метод не требует построения заранее границ области допустимых ограничений и не является чувствительным к свойствам (дифференцируемости и непрерывности) моделей управления и ограничений. В результате чего данный метод нашел свое применение в научных работах как отечественных, так и зарубежных ученых [16–19].Оптимизация цикла проводится МДП по аналогии с оптимизацией транспортной задачи, требующей нахождения оптимального маршрута на разветвленной сети дорог из начального пункта в конечный [15]. Применительно к оптимизации цикла шлифования дорожная схема аналогична «вариантам состояния процесса» при разных подачах на различных частях припуска. В нашем случае начальный пункт – это исходное состояние процесса (параметры заготовки, характеристика инструмента и т. д.), конечный пункт – это конечное состояние процесса (параметры готовой детали по точности и качеству, основное время и т. д.). В результате возникает задача отыскания цикла, имеющего минимальное основное время среди различных возможных вариантов циклов. При этом должны учитываться разные технологические ограничения и переменные технологические факторы.

Поскольку управление фактически снятым припуском осуществляется через ступенчатое изменение программной подачи, то с увеличением числа ступеней возможно максимально приблизить величину фактически снятого припуска к области ограничений, увеличив тем самым произ- водительность цикла. В идеале бесступенчатый цикл, т. е. цикл с плавным изменением программной подачи будет являться самым производительным, так как он потенциально может обеспечить полное совпадение траекторию фактически снятого припуска с границей области допустимых значений и тем самым достичь теоретического предела производительности цикла. Однако увеличение количества ступеней цикла целесообразно вести до определенного предела, так как в дальнейшем не обеспечивается значимый прирост производительности. Количество ступеней является параметром управления цикла и подбирается для определенных условий обработки с целью обеспечения высокой производительности. При проектировании цикла внутреннего шлифования оптимальное количество ступеней должно определяться из условия, когда при добавлении новой ступени прирост производительности цикла должен составлять не менее 5 %, так как в противоположном случае усилия по наладке и управлению операцией не оправдываются [20].

Рассмотрим процедуру поиска оптимальной траектории цикла на примере внутреннего шлифования. Графическое представление взаимосвязи параметров управления циклом представлено на рис. 2. К ним относятся радиальная подача ( S_pad , мм/ход), скорость осевой подачи ( V Soc , мм/мин), припуск ( П , мм), число ступеней цикла ( Z , шт.). Для упрощения понимания методики проектирования оптимальных циклов количество рассматриваемых единиц оптимизируемых параметров сокращено до минимально возможного значения.

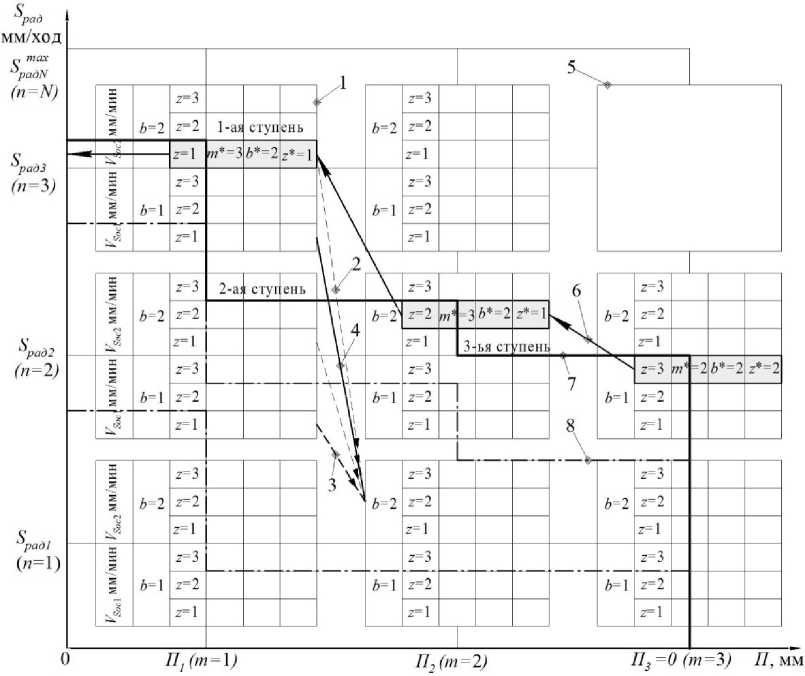
Рис. 2. Координатная сетка для оптимизации цикла внутришлифовальной обработки МДП при учете ограничения по допустимому количеству переключений подач: 1 – информационная клетка; 2 – конкурирующие ходы; 3 – допустимые ходы; 4 – оптимальный ход; 5 – выбывшие из расчета информационные клетки; 6 – процедура обратного хода; 7 – траектория оптимального управления; 8 – возможные варианты циклов; n* , b* , z* – координаты, откуда был сделан предшествующий ход

МДП требует проведения дискретизации управляющих параметров, так как он относится к методам дискретной оптимизации (см. таблицу). Состояние процесса на сетке будет характеризоваться координатами [ m , n , b , z ], которые в дальнейшем будем называть координатами состояния процесса шлифования. На каждом пересечении координатной сетки помещена «информа-

Расчет и конструирование

ционная клетка», содержащая в себе следующие данные: оптимальное время достижения состояния, текущие размеры обрабатываемой поверхности, силы резания и др. Определение минимального времени достижения состояния определяется по средствам перебора возможных вариантов переключения подач внутри проектируемого цикла – конкурирующих ходов (рис. 2). Количество конкурирующих ходов зависит от множества факторов: одновременного (неодновременного) переключения скорости осевой подачи и радиальной подачи на z -й ступени, количества пригодных подач с предшествующей дискреты припуска и др.

Дискретизация управляющих параметров

Название шкалы	Дискрета	Диапазон
Радиальная подача ( n – номер радиальной подачи)	N – количество радиальных подач станка	min max [ Sрад ; Sрад ]
Припуск ( m – номер дискреты припуска)	M – максимальный номер дискреты припуска, при котором величина оставшейся части припуска равна нулю	[ П max;0]
Скорость осевой подачи ( b – номер скорости осевой подачи)	В – количество скоростей осевых подач по паспорту станка	min max [ V Soc ; V Soc ]
Ступень припуска ( z – номер ступени припуска)	Z – количество ступеней цикла	[1; Z дано ]

Согласно принципу оптимальности из конкурирующих ходов необходимо выбрать оптимальный ход, имеющий оптимальное время достижения состояния. Выбор оптимального хода осуществляется посредствам моделирования съема m -й дискреты припуска для каждого конкурирующего хода. При моделировании процесса съема металла производится расчет величины фактически снятого припуска, текущих значений радиусов обрабатываемого отверстия, силы резания, времени съема дискреты припуска, времени достижения состояния и др. [11–14]. Конкурирующий ход участвует в выборе оптимального хода, если в достигнутом состоянии [ m , n , b , z ] выполняются все ограничения целевой функции. Ограничения целевой функции подразделяются на две группы. К первой группе относятся ограничения, накладываемые в конце цикла (точность, бесприжоговость, шероховатость обрабатываемой поверхности). Вторая группа – ограничения, накладываемые в течение всего цикла шлифования (по осыпаемости круга, мощности привода, допустимости диапазона подач и т. д.).

Величина фактически снятого припуска находится в прямой зависимости от радиальной и осевой подач, диапазоны управления которых определяются допустимым диапазоном станка. В результате можно предположить, что наиболее быстрое снижение величины фактически снятого припуска возможно при минимально допустимых значениях радиальной и осевой подач. Тогда проверка выполнения ограничений в конечном состоянии процесса сводится к ответу на вопрос, можно ли после снятия m -й части припуска успеть снизить величину фактически снимаемого припуска за время съема оставшейся части припуска при минимальных радиальной и осевой подачах до значения, при котором выполнятся ограничения первой группы. Если ответ на данный вопрос отрицательный, то тогда за время съема оставшейся части припуска при любых других больших значениях радиальной и осевой подач из допустимого диапазона подач выполнить эти ограничения тем более невозможно. Назовем данное действие принципом проверки допустимости хода. В результате проверка допустимости хода по ограничениям первой группы (точности, прижогу и шероховатости) сводится к следующей типовой процедуре. После моделирования съема металла для координат [ m , n , b ] (совершения хода) производится аналогичное моделирование съема оставшейся части припуска при минимально допустимых по станку подачах – координаты [ m max , n min , b min ]. Таким образом, из всех конкурирующих ходов выбираются только допустимые ходы. А уже из совокупности допустимых ходов выбирается оптимальный ход, имеющий оптимальное время достижения состояния и допустимый по всем ограничениям. Затем в клетку записывается номер радиальной и осевой подач, номер ступени, откуда произведен оптимальный ход. Запомненное значение уровня, откуда произведен оптимальный ход, фиксируется для каждого состояния [ m , n , b , z ] и хранится в переменной n* , b* и z* (рис. 2). Исключения составляют пересечения координат [ m , n , b , z ], не имеющие ни одного допустимого хода.

Процесс оптимизации начинается с выполнения совокупности прямых ходов на первой дискрете припуска. Затем производится переход из предыдущей дискреты припуска ( m _-1) при n -й радиальной подачи и b -й скорости осевой подачи круга в m -ю дискрету припуска. После рассмотрения последней дискреты припуска m = M из ряда оптимальных ходов, расположенных на различных номерах радиальных подач, выбирается один ход, имеющий минимальное время достижения конечного состояния (минимальное время цикла). Для фиксации оптимальной траектории управления циклом шлифования выполняется процедура обратного хода, которая начинается из хода, имеющего минимальное время достижения конечного состояния. Восстановление траектории управления цикла происходит по координатам предыдущего состояния процесса n* , b* , z* , идя от конечной дискреты припуска к начальной, запоминая при этом величины подач и припусков. На рис. 2 можно увидеть графическое представление примера процедуры обратного хода, формирующей траектории оптимальной управляющей программы. После проведения обязательной процедуры обратного хода формируется оптимальный цикл внутришлифовальной обработки, представленный на рис. 3 в координатах «Радиальная подача ( S_pad , мм/ход) - скорость осевой подачи ( V Soc , мм/мин) - припуск ( П_т , мм)». На рис. 3 также можно увидеть проекции траектории оптимального ступенчатого цикла в плоскостях S_pad и П - A 1 B 1 C 1 D 1 E 1 F 1 G 12) , V Soc и П - A 2 B 2 C 2 D 2 G 12 , фактически снятый припуск и фактическую величину скорости осевой подачи. Ступенчатый цикл внутришлифовальной обработки, который представлен на рис. 3, состоит из пяти ступеней, из которых две для скорости осевой подачи ( Z V = 2) и три для радиальной подачи ( Z s = 3).

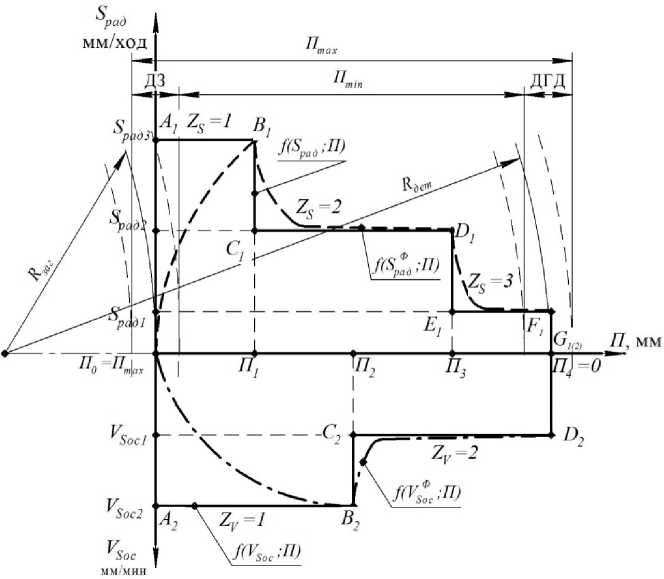
Рис. 3. Пример ступенчатого цикла внутришлифовальной обработки в двухмерном пространстве управляющих параметров

Выводы:

• 1)    отсутствие нормативно-справочной литературы и методик проектирования циклов, удовлетворяющих требованиям современного автоматизированного производства, привело к тому, что станки с ЧПУ используются на 40-60 % от закладываемой производственной мощности;

• 2)    решением проблемы является представленная в данной статье методология проектирования циклов внутришлифовальной обработки, которая:

Расчет и конструирование

• -    основывается на модели съема металла, позволяющей рассчитывать величины фактически снятого припуска, текущих значений радиусов обрабатываемого отверстия, силы резания, времени съема дискреты припуска, времени достижения состояния и др. [10-13];

• -    позволяет с математической точностью проектировать оптимальные циклы внутреннего шлифования, используя метод динамического программирования;

• -    не чувствительна к виду математических моделей (линейность, дифференцируемость) процесса и ограничений целевой функции;

• -    позволяет учитывать любое количество технологических ограничений целевой функции;

• -    учитывает изменения условий обработки (затупление зерен круга, колебание припуска и исходной точности обрабатываемой поверхности в партии заготовок);

• -    обеспечивает многопараметрическую оптимизацию управляющей программы для станков с ЧПУ на операциях внутреннего шлифования. Результатом оптимизации являются оптимальные значения радиальной подачи S_pad и скорости осевой подачи V soc на всех ступенях цикла, оптимальное распределение снимаемого припуска по ступеням цикла для радиальной подачи S_pad и осевой подачи V soc , при которых обеспечивается минимальное время цикла (или другой целевой функции);

• 3)    применение в качестве математического метода оптимизации МДП позволяет расширить количество оптимизируемых параметров (геометрические параметры круга, величина перебега, число оборотов заготовки и др.). В результате становится возможным проведение многопараметрической оптимизации в многомерном пространстве параметров управления.