Комплексные степени одного дифференциального оператора, связанного с оператором Шредингера

В работе исследуются комплексные степени дифференциального оператора Sy в Rn+1 с комплексными коэффициентами в главной части:

д Дд2

Sx = m I+ ib- + 52(i - iXk ) дХ2, k=1             ^k

где m > 0, b = 0, A = (A1,..., An), Ak > 0,1 6 k 6 n. Комплексные степени оператора S\ с отрицательными вещественными частями на функциях _V(x,t) е Ф(Rⁿ⁺¹), где Ф(Rⁿ⁺¹) -пространство Лизоркина (см. п. 2.2), определяются в образах Фурье равенством

——^^                            n \ а/2

^(S-а/2 Д⁽© ^т) = m^{2 +} йт — ^|40|^{2 +} i X ^Ak£2 j     Д©^т).

k=1

3-^ 4 ^...ДВ € Г. т € R1. Reа> 0.

Получены интегральные представления комплексных степеней (2) в виде интегралов типа, потенциала, с нестандартной метрикой. Соответствующие дробные потенциалы имеют вид:

где

(H V^)(x,t)= j

Rn+1

α h\ (У, sMx - У, t - s) dy ds,

x е Rⁿ, t е R¹,

α-n-1

α h\ (y,s)= dn,a(A)(s)+ 2 exp

[• У- X k=1

b^(Ak - i^yk 4(1 + Ak )s

b(n^-a)/2    ( -Ц-п ni)

dn,a(A) = --------^---—.

(4п)п/2Г(a) Q Х Щ k=1

Установлены оценки для оператора Н^ из Lp в Lq. В рамках метода аппроксимативных обратных операторов, построено обращение потенциалов На у, у Е L_p. Дано также описание образа Н^а (L_p) в терминах обращающих конструкций.

Таким образом, в работе получены явные выражения для комплексных степеней Sa/2у с положительными вещественными частями и описаны области определения этих степеней.

В настоящее время имеется ряд работ по теории комплексных степеней дифференциальных операторов второго порядка, с постоянными коэффициентами (см. [4, гл. 9, 11]), обзорную статью [2], а. также работы [3-9]). Рассмотренный здесь случай оператора. (1) является одним из наиболее трудных, что обусловлено анизотропностью соответствующих дробных потенциалов (т. е. комплексных степеней оператора. (1) с отрицательными вещественными частями). Последнее, в свою очередь, связано с наличием комплексных коэффициентов в главной части оператора.

Ранее, в статье [10], был исследован дифференциальный оператор i-gt + Pn₌₁(1 - iA_k ) dX2, представляющий из себя оператор Шредингера

•2 X _dL ^{% 91 +} Г1 dx"k, k=1 k

возмущенный комплексными коэффициентами в главной части. Далее, в статье [11], был изучен дифференциальный оператор m2I + igt + Pn=1(1 - iAk) Ц2, связанный с опера-xk торами Шредингера (5) и Гельмгольца m2I + РП=1 уфт• В данной работе рассмотрен dxk наиболее общий случай.

• 2.    Вспомогательные сведения

  • 2.1.    Обозначения, hf, w) = JR_n+1 f (x, t)w(x, t) dx dt; (W^y)(x, t) = (w(-, 5) * y)(x, t) — интеграл Гаусса. - Вейерштрасса. где w(x,t,5) = (4п5)^-п/2e^{(-|x|2 -}t^2)/(45) - ядро Гаусса -Вейерштрасса: S - класс Шварца быстро убгдватопщх гладких функций: R_o - банахова алгебра преобразований Фурье функций, интегрируемых в Rⁿ; C_o(Rⁿ⁺¹) = {f : f Е C (Rⁿ⁺¹), f (to) = 0} - пространство непрерывных функций, исчезающих на бесконечности.

• 2.2.    О пространствах Лизоркина Ф, Ф. Через Ф обозначим класс функций из S, которые исчезают вместе со всеми своими производными на совокупности координатных гиперплоскостей в Rⁿ⁺¹: y1 = 0, • • • ,y_n+1 = 0.

Лемма [4, лемма 1.31]. Пусть функция f (x,z) аналитична по z в некоторой области D С C лля по^тmi всех x Е Rⁿ⁺¹ п имеет суммпру:мую мажоранту: |f (x,z)| 6 F (x) Е L₁(Rⁿ⁺¹). Тогда iштеграл R _Rn+i f (x, z) dx апалптжюп no z в области D.

Пространство Ф является счетно-нормированным пространством, полным относительно набора, попарно-согласованных норм, задаваемых равенствами

H^kN =          sup          (M (u))^N |Dk ^(u)|, N = 0,1, 2,...,

|k|6N, n+i ueRn+1\ U {yeRn+1: yl=o} l=1

ГТ- u = (xA M (u = max{ Щ+Щ, Ш- ^ = mm^...,,^ j

Обозначим через Ф = Ф(Rⁿ⁺¹) пространство прообразов Фурье функций из Ф: Ф = F ^-1(Ф). Пространства Ф и Ф были введены П. И. Лизоркиным (см., например, [13]). Нам понадобится информация о плотности класса Ф в Lp.

Замечание 1. Известно [4, теорема 2.1], что Класс Ф плотен в Lp, 1 < p < то, и в C₀(Rn⁺¹). Как показано в [4. глава 2. §4]. для любой функции w(x,t) € S существует последовательность функций w_N(x,t) € Ф. аппрокстшрующая w(x) по иормо Lp . 1 <  p <  то. ii по норме Co-

• 3.    Основные результаты

ЗЛ. Интегральные представления для комплексных степеней S-^а/2у, у € Ф. Комплексные степени S-^a/2^, у € Ф , определим равенством (2). Интегральное представление для указанных степеней дает следующая

Теорема. Пусть 0 < Re a + 2. у € Ф. Тогда

(s-^a/2 у ) ( x,t ) = ( H«y ) ( x,t ) ,                              (6)

где HX - опсратор (3).

C Утверждение теоремы будет следовать из равенства

• 1_    Г Г ^у 1Д ^т HpHxi - «^т ) ds   = I £ (y,s)y(x -   - s ) dyds,

(2 n ) n⁺¹                         n                 a/2 J X ,           У,              ,

R¹ Rn I m² + Ьт + P (iXk — 1)^2 )       Rn⁺¹

k=1

где hX (y,s) - ядро (4). Для доказательства (7) установим вначале формулу

¹   [тт[

(2 n ) n⁺¹

R1 Rn

<Ж ^т ) ^ex P

n

^{— e р} Yk €k k=1

m² + Ьт

-

ixS — itT

dξ

n             a/2

— P YkP+ ie k=1

j h^a,_E(y,s)y(x — y,t — s ) dyds.

Rn+1

Здесь Re a > 0. Yk = 1 — i^k- ha,E(y,s) =

b^{(n - a})^/2 e _X p( — «Tri )

n

(4n)n/2Г(a) П vYk k=1

m²i — ^eA

( eb + is ) ^n/2 exp ь --- I

n s — X k=1

by2

4 Yk (be + is )

-2+Reα

( s ) + ²

Yk >  0. k = 1 ,..., n.

Заметим, что ha,_£ ( y,s ) € L1.

С помощью формулы Бохнера (в Rn)

получаем:

x

-~-

^_е ( ^,т ) =

∞

2exp( —^ani )

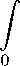
exp ( —ep + ibтp + im²p ) p^1-a/2 ( e + ip)^n/2

dρ

n

X Yk sk k=1

1-n/2 ^

Jn-2 2

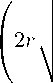
n

X Yk ^S2

k=1

dr,

где Jn-2 (z) - функция Бесселя порядка n-2. Применив к внутреннему интегралу в правой частп формуту 6.631.4 из [14]. имеем ha^ ) =

г( a)

∞ exp (-ani/4)

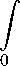
n

-ер + i m² + Ьт - P YkE2 P

V          2=1

n e P Yk Ek k=1

dρ.

Используя далее формулу 3.381.4 из [14], будем иметь:

/ n                      n           \ —a/2

ЦД^т )=^exP l^-e X Yfc<² 1 m^{2 + bT -} X Yk^ ⁺ iej    .         (9)

k=1                   k=1

Умножив обе части (9) на $(фт ) и применив обратное преобразование Фурье, получаем (8).

Заметим, что обе части (8) аналитичны по Y1 в области D 1 = {Re Y1 > 0, Im Y1 < 0}. Аналитичность правой части этой формулы обосновывается применением леммы 1 с учетом равномерной (в области D1) опенки

|hO.,_e(y,s)| 6 C (e²b² + s²)^-n/4, "^ьм ■' Rep.                       (io)

Аналитичность левой части (8) очевидна.

Анализ доказательства, граничной теоремы единственности И. И. Привалова, приведенного в [1, с. 413-415], показывает, что равенство (8) справедливо для Y1 € D1, Y2 > 0,...,7„ > 0

Далее, зафиксируем Y1 € Di и распространим по аналитичности формулу (6) для Y1 € D 1 11 Y2 € D₂ = {Re y₂ > 0, Im y₂ < 0}.

Продолжая процесс последовательного аналитического продолжения (по переменным Y3,...,Yn)- убеждаемся в справедлпвоетп (8) для Yk € Dk = {Re Yk >  0,Im Yk < 0}. k = 1,..., n.

Полагая в (8) Yk = 1 - iX_k. k = 1,... ,n. X₂ > 0. будем иметь:

PP E(iXk -1)^ -ix^-itT

¹    [ _a [ ж ^т ) • expk^¹ ______________ d ^E

(2n)n+1 /     J /            n                 \a ²

r+   Rn  m2 + Ьт + P (iXk - 1)Ek + ie I k=1

= j hx/y^Mx ^- y,t ^{- s)} dyds, v ^{€ ф} (n)

Rn+1

где

, a                                 -2+Re«     J (m ² i - e)s   ^X b^{( i} b£ ^{+ s )( X} k ^{- i )}y ² 1

hx,_e⁽y, ^{s )}= dn,a ^{( X )( eb + is )} / ^{( s )}+ ^{2   eX}P|-----b--2^1 ₄(_{1+ X} k )( _e 2 _b 2 _{+ s} 2 ) J •

Переходя в (11) к пределу при е ^ 0, получаем (7). Предельный переход в правой части (11) обосновывается мажорантной теоремой Лебега, применимой с учетом оценки

//

R¹ R ⁿ

|v^{( x -} у-Л- ^{s )|} n+2-Re a

|s|         2

dy ds < ∞,

Re a < n + 2.

Возможность предельного перехода, под знаком интеграла, в левой части (11) очевидна. Применяя к обеим частям (7) преобразование Фурье, получаем (6). B

• 3.2.    Действие оператора H- в L p-пространствах. Д ействие оператора H- из L_p(Rⁿ⁺¹) в Lq (Rⁿ⁺¹) описывается следующей теоремой.

• 3.3.    Обращение потенциалов f = НЗ р с L p-плотностями. В рамках метода аппроксимативных обратных операторов, левый обратный к S- ^a/2 оператор будем строить в виде:

Теорема 2. Оператор H— ограничен из Lp в Lq. 0 < Re a < n + 2. 1 6 p < Rn+a.. =   (n+2)p q n+2-p Re a '

Утверждение теоремы 2 легко выводится из [15, теоремы 28.2, с. 412], содержащей (Lp - Lq )-оттеики для параболических потопциалов Джонса - Сэмпсона в Rⁿ⁺¹.

a              (Lp (Rn+1)) a

(T-f)(x,t) =   lim   (Т5Д f )(x,t), где

(Taxf ^)(x,t) = j ra x ⁽y^{,s)f (x -}

Rn+l

y, t - s ) dy ds,

rax ⁽ y ^,s) =F¹

n       \ a/2

m^{2 +} b^T - ^{|e| 2 +} i X Xk(k J k=1     /

€i ei + i6

d e-S|5|2 (y,s),

⁶ > ⁰ d>n ^{+ 1} —

Справедлива, следующая

Теорема 3. Пусть ⁰ <  ^{Re a +} 2. ¹ 6 p < R+a. p g Lp. Тогда ^(T- H- P ^)(x,t) = P ^(x,t) -

Предел по норме- Lp в (12) можно заменить пределом почти всюду. C Заметим, что функция

n        a/ 2

m2 + bT - |e|2 + i X Xkek I k=1     /

...) d ^exp (^-< ² )

принадлежит R q согласно теореме 3.5 iгз [4]. Следовательно, г.д (y, s) G Li- Доказательство равенства. (14) основано на. представлении

αα

(T8,xHx P ^)(x,t) = (WMs p)(x,t) + ⁽W6 ^)(x,t).

Здесь 0 < Re a + 2. р G Lp. 1 6 p< R+.. Onojзатор M₅ имеет вид

где

d

(Ms p)(x,t) = ^C (-6)j Дy)(x,i), j=1

(Ajp)(x, t) = j... J--^⁺-^+yj Mx1 - y1

| {z }

j

- ... -

yj ,x₂, ...,xn,t) dy i ... dyj .

Равенство (15) проверяется переходом к образам Фурье для v € Ф, с учетом формулы

-—-

^([ v⁾⁽£,^T ) =

d

£1 + i5

-

¹ ЬЖ^Т), V ^{€ Ф}-

Это равенство распространяется по ограниченности на все Lp, 1 < p < Rn+2, с учетом того, что операторы в обеих частях (15) ограничены из Lp в Lq, q = n^-p R _а •

Ограниченность оператора в правой части (15) из Lp в Lq вытекает из теоремы Юнга о свертках, с учетом очевидной otkhikii kM_s vkp 6 C || vkp ii ограниченноети оператора W_s из Lp в Lq д.тя 1 6 p 6 q <  то.

а а

Оператор Ts-^Н- ограшпен из Lp в Lq по теореме 2. в силу того, что T'

δαλ

свертки с интегрируемым ядром.

В случае, когда V € Li. равенство (15) доказывается вначале в смысле Ф0 :

αα hTs,-Н- г-ш) = hWsMsV + WsV^i,  ш G ф.( О )

Пусть ш(x,t) € имеем

далее ШN (x,t) — последовательность функций S по норме Lq. q = _n-R+|__ _{п по} норме C _(ок

Ф замечание 1). В силу (17)

αα hTs-x Нх v,ШN i = hWs Ms V + Ws V,ШN i.(18)

Переходя в (18) к пределу при N ^ то. получаемт (15) для v € L1.

В [2] показано, что если g(x,t) € Lp. 1 6 p< то. то

(WsMsg)(x,t) ^ 0

Lp

Переходя в (15) к пределу при 5 ^ 0 в указанном смыс.те. получаем (14). B

• 3.4.    Описание образа H^Lp). Через Н^а ( Lp ) обозначим обгтаз оператора Н ^а:

^Н- ^(Lp) = { f ^{(u) :} f ^(u) = ^(Н5 V ^)(u) , V ^{€ L}p}-

Основной результат статьи составляет следующая

Теорема 4. Пусть 0 < Re a + 2. 1 6 p < g+2. q = ^д+^2:1д^. Тогда e ^a           n n^T p e ^a

Н- (L p ) = {f € Lq : T - f € Lp}.

C Вложение

Н а (Lp) C {f (u) € Lq : T - f € Lp}                        (20)

вытекает из теорем 2 и 3.

Докажем вложение

^Нх ^(Lp) ^D {^{f (u) € L}q ^{: T}x^{f € L}p}, обратное к (20).

Пусть f € Lq. Обозначим v = T'\f- Справедливо равенство hH-V,^i = hv,нaа^i, ш € ф, которое обосновывается применением теоремы Фубини с учетом (Lp — Lq)-оценок оператора НД. приведенных в теореме 3. Здесь Н- - оператор с символом

n

-

\ а/ 2 i)€kj

m2 + Ьт +   (i\k k=1

Далее имеем hH-'у, wi = /у, Н-'шЕ =  й Tа.f, Н-‘ш\

А м, \v’ д /    \ s >0 "’А ’ А /

= lim /т-тf’H-ш\ = lim (/ЖН - ш\. (21) S,0 \ ^S’^A ’ ^А /    S,0 \    "^{,А А} /

Последнее из равенств (21) вытекает из того, что сходимость в Lp влечет сходимость в ф0

С учетом (21) и (15), будем иметь:

α кН- у^ = lim hf, (Ws Ms + WsM = lim h(Ws Ms + Ws )f,wi = hf,wi.     (22)

s >0                                  s ,0

Второе из равенств (22) обосновывается применением неравенства Гёльдера при p > 1 и мажорантной теоремы Лебега при p = 1.

Используя рассуждения, аналогичные применявшимся при переходе от (15) к (17), получаем:

hf,wi = hHAУ’Ш^’ ш G S’ откуда вытекает, что f(x,t) = (НДy)(x,t) для шлitii всех x G Rn t G R1. Следовательно. f(x,t) G НД(Lp). B