Комплексный расчетный анализ прочности лопаток компрессора при их повреждении посторонними предметами

На сегодняшний день требования к надежности газотурбинных двигателей неуклонно возрастают. По данным эксплуатационной статистики, основной причиной того, что двигатели досрочно снимаются с эксплуатации, являются поломки лопаток. Лопатки компрессора ГТД испытывают в общем случае сложный комплекс статических и динамических нагрузок, которые приводят к накоплению повреждений в лопатке по механизмам малоцикловой и многоцикловой усталости соответственно. До 60 % поломок лопаток компрессоров ГТД носят усталостный характер. С точки зрения надежности двигателя необходимо обеспечить прочность не только целых лопаток, но и лопаток с повреждениями и зачистками. Цель работы - разработка методики для комплексного расчетного анализа прочности лопаток компрессора при их повреждении посторонними предметами.

Неотъемлемыми элементами комплексного расчетного анализа прочности лопаток компрессора при их повреждении посторонним предметом (ПП) являются:

• •    математическое моделирование соударения лопатки с ПП;

• •    расчетная оценка снижения усталостной прочности лопаток с повреждениями;

• •    расчетная оценка влияния повреждения на модальные характеристики лопатки.

Основными факторами, влияющими на повреждения лопаток ПП, являются: форма, размеры и материал ПП, скорость и направление его движения относительно лопатки, а также материал, размеры и форма лопатки.

Анализ эксплуатационной статистики, приведенной в [1], показал, что геометрия ПП, материал и скорость его движения весьма разнообразны; в большинстве случаев идентифицировать ПП, явившийся причиной повреждения лопатки, не удается. Скорость столкновения с ПП, по некоторым оценкам, близка к окружной скорости. Угол соударения 30...60° от направления хорды профиля лопатки со стороны корыта.

Рис. 1. Виды повреждений лопаток ГТД: вмятина, разрыв, забоина

Согласно эксплуатационной статистике, приведенной в [2] и [3], повреждения лопаток компрессора высокого давления обычно представляют собой вмятины, забоины или разрывы (рис. 1). Обычно они появляются на входной кромке и имеют характерные размеры в пределах нескольких миллиметров; забоины имеют форму, близкую к полуокружности.

Для математического моделирования процесса повреждения лопаток в большинстве изученных публикаций [3-5] успешно используется метод конечных элементов (МКЭ) в динамической постановке. Применение специальных аппаратов для численного моделирования позволяет учитывать следующие особенности процесса соударения:

• •    нестационарный, динамический характер процесса;

• •    трехмерное динамическое напряженно-деформированное состояние лопатки;

• •    нелинейное поведение материала, возникновение в лопатке в процессе соударения необратимых деформаций и разрушения;

• •    сложная, не описываемая в аналитическом виде форма исследуемого объекта - лопатки компрессора;

• •    геометрическая нелинейность - большие деформации, нелинейность граничных условий (контактное взаимодействие лопатки с ПП).

Задачи статики с необходимостью учета сложной геометрии конструкции, нагружения и закрепления также возможно решать с применением МКЭ. Для решения динамических быстропротекающих нелинейных задач с помощью МКЭ целесообразно использование явного метода интегрирования по времени, статические задачи решаются с помощью неявного метода.

В ходе исследования была разработана методика математического моделирования соударения лопатки с ПП. Методика направлена на математическое моделирование ситуаций, соответствующих типичным повреждениям лопаток, выявленным в ходе эксплуатации. Моделирование соударения позволяет выявлять закономерности процесса соударения лопатки и ПП.

Объектом данного исследования являются лопатки направляющего аппарата 5-й ступени компрессора высокого давления. Лопатка имеет переменный по высоте аэродинамический профиль. Высота лопатки 70 мм, хорда составляет 26,6 мм. Лопатки закреплены в двигателе консольно замком типа «ласточкин хвост».

Задача ставилась в следующей постановке. Стальная линейноупругая сфера диаметром d = 4,48 мм движется поступательно со скоростью V по направлению к входной кромке неподвижной лопатки под углом а к хорде, лопатка неподвижно закреплена в корневом сечении (рис. 2). Материал лопатки - титановый сплав, материал считается упругопластическим, способным разрушаться. Высота соударения вдоль пера лопатки соответствует высоте наиболее опасного сечения реальной лопатки - сечения, в котором имеют место максимальные динамические напряжения при колебаниях по первой изгибной форме. Для лопатки 5-й ступени это высота 14 мм от корневого сечения лопатки.

Для анализа влияния на процесс соударения различных факторов было реализовано несколько схем соударения. Схемы соударения характеризовались:

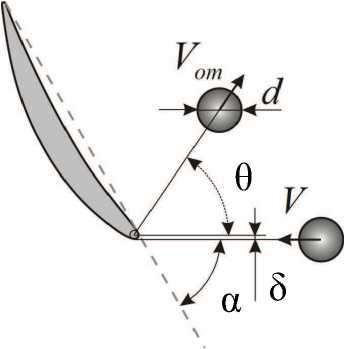
Рис. 2. К постановке задачи соударения лопатки с посторонним предметом

• •    скоростью ударника V по направлению к входной кромке;

• •    углом а к хорде лопатки, под

которым происходит соударение.

Для описания движения деформируемой сплошной среды используется лагранжевый подход. Решение трехмерной динамической задачи в МКЭ заключается в разрешении системы уравнений, в которую входит уравнение сохранения импуль са, движения, внутренней энергии, замыкает систему определяющее соотношение:

• •    уравнение сохранения импульса р - div( v ) = 0, где р - плотность; v - скорость;

• •    уравнение движения р - x = div( o ),                              (1)

где x - ускорение, о - тензор напряжений;

• •    уравнение сохранения энергии, без учета тепла и температуры р ^- U = о : £ ,                             (2)

где U - скорость изменения внутренней энергии, £ - тензор деформации скорости, «:» - двойное скалярное произведение;

• •    определяющее соотношение о = f ( £ , £ ) ;

• •    геометрические соотношения для случая больших деформаций

• ^{2 s} ij ( х, t ) = ( uу ( x, t ) + u ji ( x, t ) + u m ( x, t ) • u _m-i ( x, t ) ) , x e V .

Система дополнена граничными условиями:

• •    кинематические граничные условия (заделка лопатки в корневом сечении):

d i = 0 x еГ d x = ( x , y , z ) ;

• •    статические граничные условия на свободной поверхности (начальное ненапряженное состояние):

j = ⁰ x ^еГ о ;

начальные условия:

x i = ⁰ , x ^{е Г} лоп ;

x Шар =-240 (м/с), x е Г шар -

y шар = ⁰, z шар = ^{0 ;}

• •    наличие контактного взаимодействия лопатки с посторонним предметом.

Особенность граничных условий в зоне контакта - неизвестные изменяющиеся во времени размеры и форма площадки контакта, неизвестные нагрузки на этой площадке. При моделировании динамического контактного взаимодействия в МКЭ применяется метод пенальти, в соответствии с которым в расчет условно вводится упругая пружина, расположенная между контактирующими поверхностями и определяющая жесткость взаимодействия или величину контактной силы. Контактная площадка определяется с помощью скалярной функции G ( x , y , z ) , описывающей поверхность одного из соударяющихся тел - мишени. При G ( x , y , z ) >  0 точки ударяющего тела лежат вне поверхности, при G ( x , y , z ) = 0 точки на поверхности, G ( x , y , z ) < 0 означает проникновение ударника в мишень. В последнем случае для предотвращения проникновения в соответствующий узел прикладывается противодействующая сила. Согласно методу пенальти, противодействующая сила пропорциональна величине проникновения сегментов тел друг в друга и действует по нормали к поверхности.

Величина контактной силы по методу Пенальти определяется следующим образом:

f = pdN ( X n ) , где p - эффективная жесткость условной пружины, «коэффициент пенальти»; d - величина проникновения, N - нормаль к поверхности.

После пространственной дискретизации решение уравнения движения (1) при использовании МКЭ сводится к решению дифференциального уравнения • •

M d = F , + F , ,                         (3)

где d - вектор узловых ускорений; M - матрица масс; F , F , - векторы внутренних и внешних сил.

Узловые ускорения могут быть определены из уравнения (3) и записаны следующим образом:

d = M - 1 ( F , + F , ) .

Использование центральной дифференциальной схемы интегрирования во времени (временная дискретизация) позволяет определить значения ускорений, скоростей и перемещений по схеме d n = M-1 (F, + F,),

•                   •                 ее d 1 = d 1 + dn At,                          (4)

n +       n -

22 f d n+1 = d n + d 1 A t • n+

Центральная дифференциальная схема интегрирования (4) во времени устойчива в том случае, если выполняется критерий устойчивости, известный как условие Куранта,

Ах ■

At <Аtcr = —min , c где c - скорость звука в материале; Axmin - минимальный характерный размер входящих в рассматриваемую систему элементов.

Для описания поведения материалов при высоких скоростях деформирования широкое распространение получила упругопластическая модель поведения материала Купера-Саймондса (Cowper-Symonds). Она учитывает кинематическое упрочнение и влияние скорости деформации. Для учета влияния скорости деформации на предел текучести материала вводится масштабирующий коэффициент, который определяется как

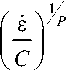
о T™ = о T р,   р = 1 + где ё - скорость деформации; C, P - константы материала. Для реализации поведения материала в соответствии с описанной моделью в программном комплексе ANSYS использовалась модель поведения материала Piecewise Linear Plasticity Model (кусочно-линейная пластическая модель).

Разрушение материала лопатки моделировалось удалением элементов, в которых деформация превышала предельное значение г B . Расчет завершался по окончании процесса соударения и пластического деформирования лопатки.

Для проведения численного моделирования были созданы модели лопатки и ударника. Были приняты следующие допущения:

• •    В геометрической модели лопатки не учитывается изменение профиля по высоте. Модель лопатки имеет постоянное по высоте сечение, которое соответствует наиболее опасному сечению реальной лопатки.

• •    Закрепление лопатки в замке моделируется жесткой заделкой в корневом сечении. Лопатка рассматривается как жестко защемленная консольная балка.

Конечно-элементная сетка состоит из призматических изопарамет-

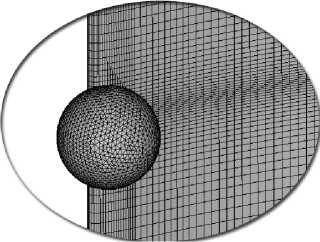
Рис. 3. Пример конечно-элементной сетки лопатки и ударника

рических 8-узловых элементов с линейной аппроксимацией (рис. 3). Размер конечного элемента в зоне соударения выбирался таким, чтобы характерный размер ожидаемого повреждения был на порядок больше. Размер элемента составил 0,08 мм. Размер элемента на удалении от повреждения составляет 0,5 мм. Конечно-элементная сетка ударника состо ит из изопараметрических тетраи-дальных элементов (см. рис. 3) с характерным размером 0,2 мм.

Проведен анализ и количественная оценка эффектов, возникающих в процессе соударения лопатки с ПП. При соударении в лопатке начинается процесс распространения, отражения и взаимодействия волн напряжений, пластическая деформация и разрушение, по окончании соударения лопатка совершает свободные колебания. При моде- лировании удалось реализовать три наиболее часто встречающихся в эксплуатации типа повреждения: вмятина, забоина (вырыв), разрыв (рис. 4). Установлено, что существует критическое значение кинетической энергии ПП, при которой происходит смена механизма повреждения лопатки: разрушение с образованием вмятины сменяется на разрушение с образованием вырыва и потерей массы (см. рис. 4). Получено количественное значение этой энергии для лопатки 5-й ступени компрессора высокого давления при ударе со стороны корыта. Это значение Е('Т = 18,5 (Ккрит = 325 м/с).

После отскока ПП лопатка совершает колебания с собственными частотами и формами. Остаточные напряжения при решении задачи с помощью МКЭ могут быть получены путем введения демпфирования в систему. Гашение колебаний в системе начинается после момента прекращения контакта лопатки с ПП.

Диапазон возможных собственных частот колебаний системы разбивается на перекрывающие друг друга интервалы; в этих интервалах частот вводится постоянное демпфирование. Процесс гашения колебаний занимает 40 мкс (для сравнения процесс соударения длится 35 мкс). В результате

E

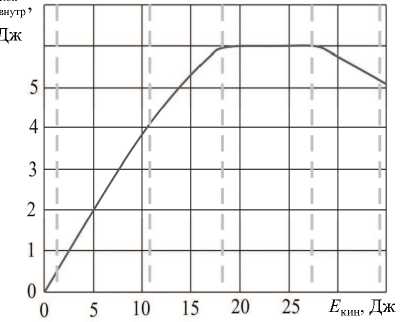
Рис. 4. Зависимость работы пластического деформирования от кинетической энергии постороннего предмета

установлены закономерности распро-

странения остаточных напряжений в лопатке при ударе со стороны корыта под углом к хорде лопатки а = 60 ° . Удар происходит с образованием вмятины.

На рис. 5 представлены зависимости изменения нормальных напряжений вдоль пера лопатки с течением времени. Зависимость 1 -изменение напряжений в элементе из зоны со стороны корыта лопатки (остаточные напряжения растяжения); зависимость 2 - изменение на- пряжений в элементе из зоны со стороны спинки лопатки (остаточные напряжения сжатия); зависимость 3 - изменение напряжений в элементе с входной кромки лопатки на удалении от повреждения (остаточные напряжения минимальны).

Остаточные напряжения носят локальный характер и присутствуют в зоне повреждения. Максимальные растягивающие напряжения имеют место на границе вмятины со стороны корыта, максимальные сжимающие напряжения - на границе вмятины со стороны спинки (см. рис. 5). В соответствии с графиком могут быть приближенно определены остаточные напряжения в зафиксированных элементах. Элемент 1: о yy _ост = - 970 + 3,9 % МПа; элемент 2: о yy _ост = 500 + 6,4 % МПа; элемент 3: о yy _ост = 67 + 7% МПа. Сжимающие остаточные напряжения по абсолютной величине превышают напряжения растяжения в 1,9 раза.

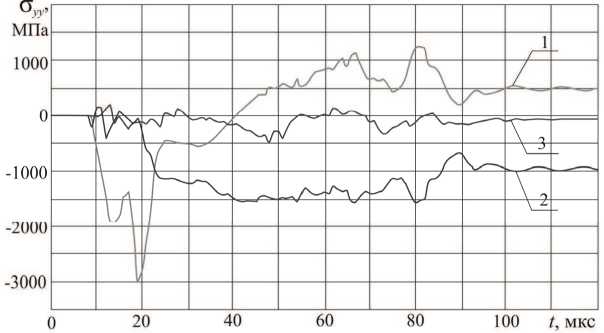
1 - остаточные напряжения сжатия (элемент в зоне сжатия со стороны спинки);

2 - остаточные напряжения растяжения (элемент в зоне растяжения со стороны корыта);

3 - разгруженная зона (элемент с входной кромки на удалении от повреждения)

Рис. 5. Изменение напряжений в элементах лопатки со временем в процессе соударения и гашения колебаний

В настоящем исследовании описывается методика оценки снижения усталостной прочности лопаток при минимальном объеме усталостных испытаний вследствие повреждения их посторонними предметами [6]. Методика опирается на определение теоретических коэффициентов концентрации напряжений а_о в лопатках. При этом проводился расчет теоретических коэффициентов концентрации и коэффициентов чувствительности к концентрации напряжений q . Для этого производились конечно-элементные расчеты по определению напряженно-деформированного состояния лопаток без повреждений и с различной геометрией повреждения: V-образная забоина, полукруглый надрез, зачистка. Расчеты производились в статической упругой постановке. Реализовывалось нагружение изгибающей нагрузкой, приложенной в центре масс периферийного сечения перпендикулярно хорде лопатки, и нагружение центробежной силой.

Были получены количественные значения теоретических коэффициентов концентрации для характерных повреждений. Полученные значения а_о лежат в диапазоне 1,76-5,92. Данные результаты дополнили существующую зависимость, что позволило подтвердить обоснованность использования ранее полученного соотношения [7] для определения теоретического коэффициента концентрации по данным о глубине и радиусе повреждения:

а_п = 1 + 1,5^/ h р . (5)

Достоверность аппроксимации результатов для данного соотно шения составляет 0,96 (рис. 6). Отклонение от этого соотношения для всех рассчитанных методом конечных элементов теоретических коэффициентов концентрации при действии изгибающей нагрузки не превышает 9 %.

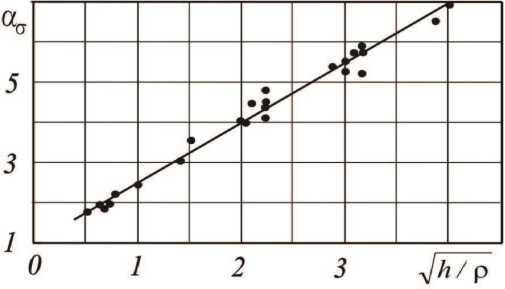
Рис. 6. Зависимость теоретического коэффициента концентрации от размеров повреждения: точки - расчетные значения ао для исследованных лопаток; сплошная линия по соотношению (5)

Получены количественные значения коэффициентов чувствительности q для титановых лопаток 5-й ступени направляющего аппарата. Эти значения лежат в пределах 0,23-0,46. Зависимость коэффициента чувствитель- ности к концентрации напряжений от теоретического коэффициента концентрации [7] дополнена вновь полученными значениями. Результаты для лопаток из титановых сплавов и стальных лопаток образуют практически непересекающиеся области. Коэффициенты чувствительности для стальных лопаток лежат в пределах 0-0,09, для титановых лопаток 0,6-0,46.

На основании полученной в результате исследования информации возможно проведение оценки снижения усталостной прочности лопаток при наличии повреждения по расчетно-экспериментальной методике, описанной в [6].

В качестве заключительного элемента предложенного комплексного расчетного анализа прочности лопаток компрессора выступает анализ влияния повреждения на модальные характеристики лопатки. Данный анализ также производился с применением конечно-элементного моделирования. Производился расчет модальных характеристик лопатки: собственных частот и форм колебаний. Для решения частичной проблемы собственных значений в ANSYS был использован метод Ланцоша (Block Lanczos). На данном этапе исследовались лопатки без дефектов, с дефектом типа забоина, с дефектом типа трещина. Трещина в расчетной оценке моделировалась разрезом нулевой толщины с прямолинейным фронтом и с реальным фронтом трещины, полученным в результате экспериментальных исследований трещиностойкости лопатки.

В результате исследования получено процентное снижение собственных частот колебаний лопатки при различных типах повреждений и произведена оценка влияния повреждения на резонансную диаграмму. Для повреждения типа V-образная забоина при глубине 1 мм максимальное снижение собственной частоты составило 0,22 %. Для повреждений типа полуокружность и зачистка снижение не превышает 2 %. Эти типы повреждений влияют на резонансную диаграмму Кемпбелла незначительно. Повреждение типа трещина при ее длине более 20 % длины хорды вызывает снижение собственных частот более чем на 3 % и значительно влияет на резонансную диаграмму.

Таким образом, в процессе исследования определен и разработан круг методик, входящих в комплексный расчетный анализ прочности лопаток компрессора при их повреждении ПП. Данный комплексный расчет произведен для лопатки 5-й ступени компрессора ГТД.