Композиция и расчет высокоразрешающих оптических систем с градиентными и дифракционными элементами

Аберрационные свойства и коррекционные возможности градиентных и дифракционных элементов хорошо изучены [1-3]. Это позволяет при компоновке исходной схемы оптической системы из таких элементов использовать подход, при котором в нее включают лишь те элементы, свойства и возможности которых необходимы, а количество достаточно для удовлетворения требований, предъявляемых к разрабатываемой системе. Эффективность подхода и относительная простота его реализации обусловлены спецификой аберрационных свойств градиентных и дифракционных элементов. Во-первых, сходимость аберрационного разложения чисто градиентной, дифракционной или гибридной градиентнодифракционной системы, выбранной в соответствии с вышеизложенным подходом в качестве исходной, такова, что устранение аберраций каждого последующего порядка приводит к ощутимому улучшению оптических характеристик. Во-вторых, градиентные и дифракционные линзы позволяют осуществлять селективную коррекцию аберраций различных порядков, что достигается с помощью коэффициентов рядов, описывающих законы изменения показателей преломления материалов градиентных линз и пространственных частот микроструктур дифракционных линз.

Здесь предполагается, что распределения показателя преломления градиентной линзы и пространственной частоты дифракционной линзы описываются выражениями вида

n ( Р ) = ^ n p Р ² p , ⁽¹⁾ p = 0

^ ( р ) =

^ 0

Ф _DL р- 2 ^ ( p + 2) b 2 p ₊ з Р ² p ^{+ 3} p = 0

В этих выражениях р- расстояние от оптической оси; n p при p =0 - базовый показатель преломления; n p при p =1, 2, ... - коэффициенты радиального градиента; O DL = 1/ f DL - оптическая сила дифракционной линзы; 2 0 - длина волны записи; b _2p+3 - коэффициенты асферической деформации эйконала записи [1-3].

2.    Компоновка исходных схем

Из изложенного во введении следует, что требования к разрабатываемой системе целесообразно выражать через аберрации, подлежащие устранению. Например, если у системы потребовать полное и одновременное устранение всех монохроматических аберраций третьего порядка, то почти автоматически при- ходим к следующим возможным схемным решениям: двухлинзовый дифракционный объектив [1]; объектив, состоящий из дифракционной и градиентной линз [2,3]; склеенная линза Вуда (т.е. оптический элемент, имеющий плоские внешние преломляющие поверхности и изготовленный из двух неоднородных материалов, разделенных сферической поверхностью склейки) [4] и компонент, состоящий из трех склеенных плоскопараллельных пластин, выполненных из двух неоднородных материалов [5].

Поставив задачу одновременного устранения у системы монохроматических аберраций третьего и пятого порядков, приходим к триплету, склеенному из неоднородных линз, ограниченных сферическими преломляющими поверхностями [6,7]; компоненту, состоящему из четырех склеенных неоднородных плоскопараллельных пластин [8]; склеенной линзе Вуда, у которой на плоских внешних поверхностях размещаются кольцевые микроструктуры дифракционных линз и к объективу, состоящему из трех плоских дифракционных линз, разделенных двумя неоднородными материалами.

3.    Определение исходных конструктивных параметров

Конкретные значения конструктивных параметров всех вышерассмотренных схем можно получить, решив систему, включающую соответствующие параксиальные и компенсационные уравнения. При этом, как правило, количество параметров превышает число решаемых уравнений и, следовательно, имеется определенная свобода выбора значений некоторых конструктивных параметров. Они могут выбираться исходя, например, из требований и ограничений, априори накладываемых на задний фокальный отрезок системы, перепады показателей преломления неоднородных материалов, максимальные значения пространственных частот структур дифракционных линз, кривизны сферических преломляющих поверхностей, толщины линз и т.д. Однако если, в конечном счете, требуется получить оптическую систему с предельными для выбранного количества используемых элементов полевыми характеристиками, то набор значений вышеуказанных свободных параметров должен обеспечить исходной схеме минимально возможный уровень остаточных аберраций высших порядков.

Поиск такого набора целесообразно производить в два этапа. На первом этапе определяются границы начальной зоны поиска, исходя из известных ограничений на значения свободных параметров, и выбирается шаг для каждого из свободных параметров, что должно обеспечить оптимальный баланс между временем и точностью поиска. Результатом этого этапа поиска явится база начальных решений. На втором этапе, по результатам лучевого расчета, выделяются решения, обеспечивающие при выбранной числовой апертуре и в пределах заданного полевого угла наинизший уровень остаточных аберраций высших порядков.

4.    Оптимизация

Выделенные решения используются в качестве исходных при последующей лучевой оптимизации. В общем случае ее осуществляют по положению входного зрачка, коэффициентам радиального градиента всех неоднородных материалов и по коэффициентам рядов, описывающих законы изменения пространственных частот микроструктур дифракционных линз. При этом оптимизация производится по коэффициентам рядов, влияющим на аберрации, начиная с того порядка малости в аберрационном разложении, который не учитывался при составлении компенсационных уравнений.

Оптимизацию, как показала практика расчетов, целесообразно осуществлять специально адаптированным методом Ньютона с использованием двух лучевых функций оценки качества точечного изображения Q 1 и Q 4 , вычисляемых для ряда полевых углов, число которых равно числу оптимизируемых параметров. Функция Q 1 , представляющая собой нормированный на рэлеевское разрешение объектива d_R средний радиус пятна рассеяния лучей и монотонно убывающая с уменьшением уровня остаточных аберраций, используется для построения целевой функции, а функция, на которой базируется наиболее достоверный из лучевых критериев оценки качества Q 4 >0,7, - для выработки команды завершения процесса оптимизации [7]. Выбор наилучшего решения и окончательная аттестация объектива, включающая оценку размера поля, в пределах которого точечное изображение близко к дифракционноограниченному, осуществляется по картине распределения интенсивности в дифракционном изображении точки. Для этого, в частности, используется критерий E (d_R ) >0,73 , ограничивающий снизу относительную энергию, приходящуюся на центральный кружок дифракционного изображения радиусом d_R, и гарантирующий, что изображение практически не отличается от дифракционно-ограниченного [1,3,9].

5.    Высокоразрешающий гибридный объектив-монохромат

На рис.1 представлена оптическая схема гибридного объектива-монохромата, состоящего из градиентного элемента, имеющего плоские внешние поверхности и изготовленного из двух различных неоднородных материалов с радиальными распределениями показателей преломления, разделенных сферической поверхностью склейки, на внешние по- верхности которого нанесены структуры дифракционных линз. Количество коррекционных параметров объектива таково, что их в принципе более чем достаточно для полного и одновременного устранения всех монохроматических аберраций третьего и пятого порядков. Однако, как показали предварительные исследования, аберрации высших порядков могут быть снижены до приемлемого уровня лишь в том случае, когда одна из аберраций пятого порядка и, в частности, дисторсия остается не устраненной.

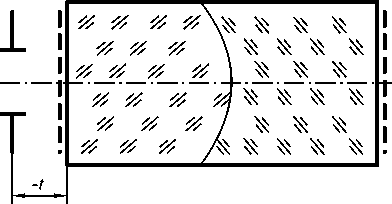
Рис. 1. Дифракционно-градиентный объектив.

При расположении предмета в бесконечности и в приближении аберраций не выше пятого порядка, оптические характеристики этого объектива определяются 17 параметрами. В это число входят оптические силы дифракционных линз Ф ^ ” ’ = 1/ f DL ” ’ , коэффициенты асферический деформации их эйконалов записи b ₃ ⁽ ” ’ и b 5 ” ’ , радиус сферической поверхности склейки r , толщины неоднородных материалов d m , их базовые показатели преломления n 0 m ) и коэффициенты радиального градиента n^ ) ( m =1-2, p =1-3).

В данный набор параметров не вошло расстояние t , определяющее положение входного зрачка, поскольку, если в оптической системе все монохроматические аберрации данного порядка устранены при некотором положении зрачка, то они отсутствуют и при любом другом его положении.

Обратимся теперь к системе уравнений, которую следует решить для определения вышеперечисленных параметров. В нее входят два параксиальных уравнения для фокусного расстояния объектива и для заднего фокального отрезка, а также 13 компенсационных уравнений, обеспечивающих обнуление пяти коэффициентов монохроматических аберраций третьего порядка и восьми из девяти коэффициентов пятого порядка. При решении системы целесообразно положить фокусное расстояние объектива f’=1 , а задний фокальный отрезок 5 'F и базовые показатели преломления неоднородных материалов n 0 m ) считать свободными параметрами.

Явный вид уравнений, обеспечивающих единичное фокусное расстояние и заданное значение заднего фокального отрезка, легко получить, воспользовавшись аппаратом гауссовых коэффициентов [10, 11, 2]. В результате имеем

¹ -ф DL вф cs в ф D2L +

(1)        (2)(2)

^{+ а} 1 ^ф DL Р 2 ^ф DL ^{+ а} 1 ^ф CS Р 2 ^ф DL ⁺

^{+ а} 2 ^ф DL ^в 1 ^ф cs + ^а 2 ^ф DL ^в 1 ^ф DLL —

• ^{—    а} 1 ^а 2 ^ф DL ^{— а} 1 ^а 2 ^ф cs —

• — а1а 2ф DL —ф DL р1 у 2 —

• -    0 2 ф DI) Y 1 + « 1 Y 2 + а 2 / , = 0

  
  

• ⁵ F = ф DL P ₁ ф _CS P ₂ — « 1 ф£ Р 2 — а ₁ ф _CS p ₂ —

— а2ФD1LР1 + Р2Y1 + «А •

Здесь ф CS =(n02) — n01))/r - оптическая сила поверхности склейки; am, вm, уm - гауссовы коэф- фициенты m -ого неоднородного материала:

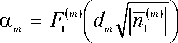
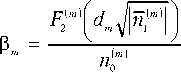
Y m

2 n 0^m ) n ⁽ m > ₽ m

где F 1 ( ... ) и F ₂ ( ... ) - функции вида

F 1 d Ti n i ) =

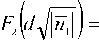
cos ( d^ — n 1 , n 1 <  0 ) ch ( d-^n" 1 , n 1 >  0 )

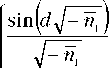
⁽ n i <  ^{0 )}

s dn ) , ( „ , >  0 )

V n

ⁿ 1 = 2 njn 0 . .                                      (7)

Из всех компенсационных уравнений третьего и пятого порядков, наиболее простой вид имеет уравнение, обеспечивающее выполнение у объектива условия Петцваля, которое, в силу автоматического выполнения этого условия у дифракционных линз, сводится к требованию его выполнения только у склеенного градиентного элемента [4]:

2 n 0¹) n 0²⁾ £ [ n ( m ⁾ d m /( n 0 m ⁾ ) 2 ] —Ф cs = 0 .          (8)

m =1

Оставшиеся четыре компенсационных уравнения, определяющие условия устранения у объектива сферической аберрации, комы, астигматизма и дисторсии третьего порядка, а также уравнения, обеспечивающие устранение любых четырех аберраций пятого порядка, имеют следующую структуру:

B 0 ( c , d m , n 0 m ) , n ⁽ m ) ) +

+ ]T n 2 m ) B m (d_nl , n 0 m ) , n ⁽ m ) ) = 0, m = 1

+ У n ( m ) C ( ф ⁽”), r , d , n ( m ) , n ( m ) ) = 0              (9)

2 m DL ^{, ,} m ^, 0   ^, 1

m = 1

для третьего порядка и и(ф(m) Z>(m) г d T7(m) T7(m) T7(m))+ \DL , ^3 , r , ^m , n0 , n1 , n2 + +

E b 5m ) V m ( ф DL) , b 3 m ) , r , d m , n 0 m ) , n 1 m ) , n 2 m ) ) + m = 1

+ E n 3 m ) W m ( ф DL) , b 3 m ) , Г , d m , n 0 m ) , n ( m ) , n 2 m ) ) = 0 (10) m = 1

для пятого порядка, т.е. аберрационные коэффициенты третьего порядка линейны относительно коэффициентов b ₃ ^{( m )} и n ₂ ^{( m )} , а коэффициенты пятого порядка – относительно b ₅ ^{( m )} и n ₃ ^{( m )} [12, 3]. В результате 11 из 15 уравнений вышеописанной системы линейны, что существенно упрощает процесс ее решения.

Поиск и исследование областей существования физически реализуемых решений рассматриваемой системы уравнений показал, что при базовых показателях преломления неоднородных материалов, удовлетворяющих условию 1,5 <  n 0 ^m ) <  2 , решения существуют в широком диапазоне длин заднего фокального отрезка объектива 0,15 f ‘ <  s' F <  0,7 f' . В результате была поставлена задача локализовать в ограниченной области трехмерного пространства ( n 0° , n 0 ²⁾, 5'_F ) зону, которой при заданной числовой апертуре объектива NA =0,27 и в пределах углового поля в пространстве предметов 2 ®< ( 15 o — 20 o ) соответствуют решения, обеспечивающие наинизший уровень всех остаточных аберраций (за исключением дисторсии). В итоге было выделено несколько решений, из которых уже по результатам оптимизации было выбрано одно, приводящее к наилучшей исходной схеме гибридного объектива. Это решение представлено в табл.1.

Результаты исследования исходной схемы и ее оптимизации приведены в табл. 2. Первый раздел этой таблицы содержит конструктивные параметры и полевые характеристики, полученные непосредственно из расчета в области аберраций третьего и пятого порядков, а второй раздел - полученные в результате оптимизации. Все данные получены при фокусном расстоянии f ’=25 мм и числовой апертуре NA =0,27, обеспечивающей на длине волны He-Cd лазера λ=0,4416 мкм рэлеевский предел разрешения δ R =1 мкм.

В табл.2 приведены: конструктивные параметры b₇, b₉, n₁, n₅ , использовавшиеся для минимизации остаточных аберраций высших порядков; параметр t , который использовался как для минимизации аберраций, так и для уменьшения перепадов показателей преломления; световые диаметры D дифракционных линз и неоднородных материалов, минимальные периоды Λ_min структур дифракционных линз и перепады показателей преломления ∆ n неоднородных материалов.

Т а б л и ц а 1

Конструктивные параметры объектива, свободного от всех монохроматических аберраций третьего и пятого порядков за исключением дисторсии пятого порядка

r/f ′	d/f ′	( 2 ) n 0	n 1 f ′ 2	n 2 f ′ 4	n 3 f ′ 6
∗ ∞
	1,3598	1,94	-0,5689	0,1735	0,1997
5,612
	0,7161	1,55	0,6508	-0,8515	-1,6612
∗∗ ∞
s ′ F = 0,58 f ′
∗ Φ DL = - 0,5920/ f ′ , b 3 = -0,13274/ f ′ 3 , b 5 = -0,96990/ f ′ 5
∗∗ Φ DL = 1,2391 f ′ , b 3 = 2,22633 f ′ 3 , b 5 = 5,63116 f ′ 5

Т а б л и ц а 2

Дополнительные конструктивные параметры и полевые характеристики объектива до и после оптимизации