Композиционный способ определения управления глазодвигательными мышцами при саккаде

Быстрое скачкообразное синхронное движение обоих глаз, осуществляемое, например, при смене точек фиксации взора, называют саккадой. В ряде литературных источников [3, 4, 8, 9, 11, 16] показано, что саккадическое движение глаза планируется до его начала и сама саккада осуществляется как программное движение, ее коррекция в случае промаха осуществляется по окончанию движения. Данная работа посвящена построению программного мышечного управления, реализующего саккаду.

Экспериментальные данные

В ходе эксперимента испытуемый находится в звуко- и светоизолированной камере в кресле с подголовником, исключающим движения головы. На светодиодном стенде, имеющем в пределах зрительного поля размер 27 × 40°, предъявляют световые точечные стимулы, один центральный и шестнадцать периферических. Испытуемого инструктируют фиксировать взор на центральном стимуле, а при появлении

Кручинина Анна Павловна, магистрант механико-математического факультета, Москва

До начала каждого экспериментального цикла взор испытуемого не фиксирован и направлен в темноте произвольно перед собой. Стимуляционный экран погашен. Цикл начинается с момента, когда включается центральный световой стимул. Чтобы исключить привыкание, длительность включения центрального стимула изменяется случайным образом в диапазоне 700–1000 мс. Затем центральный стимул выключается и одновременно включается один из периферических стимулов, длительность включения которого составляет 1000–1300 мс. Далее периферический стимул выключается и цикл повторяется. Циклограмма эксперимента показана условно на рис. 1. Эксперимент предусматривает выполнение 800 циклов.

Движения глаз испытуемого регистрируют методом электроокулографии с помощью чашечковых электродов, которые накладывают у височных краев правого и левого глаза (для регистрации горизонтальных саккад) и у верхнего и нижнего краев правого глаза (для регистрации вертикальных саккад). Электроокулограмму записывают в файл с частотой 512 Гц. В этот же файл синхронно записывают отметки о включении стимулов на экране.

Обработка экспериментальных записей

В данной работе рассматривались только горизонтальные саккады, возникающие при переводе взора на периферический стимул, находящийся справа от центрального стимула под углом в 20°. В экспериментальном файле имелось 63 таких записи. Саккады характеризовались максимальной скоростью 300 ± 30°/с и длительностью 0,05–0,08 с.

Для определения управления, подаваемого на глазодвигательные мышцы, необходимо нахождение первой и второй производных программного угла поворота глаза. Однако оказалось, что численное дифференцирование цифровой записи затруднительно из-за высокочастотного шума, который плохо удалялся с помощью процедур сглаживания. Поэтому для каждой записи траектория глаза аппроксимировалась функцией Больцмана вида

_Ф ( t ) = A 1 --2^ ,                                   (1)

• 1    + e^D

где t е [0; T ].

Данная функция содержит четыре неизвестных параметра, значения которых для каждой саккады определялись методом наименьших квадратов. Такая аппроксимация оказалась очень удачной (рис. 2): при общей амплитуде скачка в 20° среднеквадратическое отклонение подобранной функции (1) от записи имело величину около 0,2° на саккаде, содержащей в среднем 30 измерений.

Центральный стимул

Периферический стимул

Движение глаз

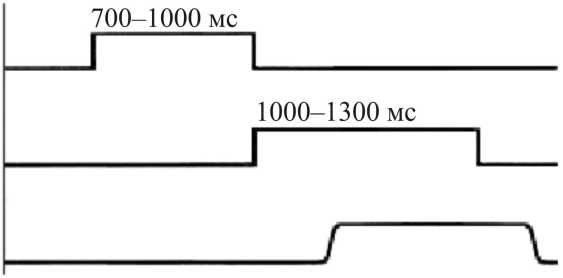
Рис. 1. Циклограмма эксперимента

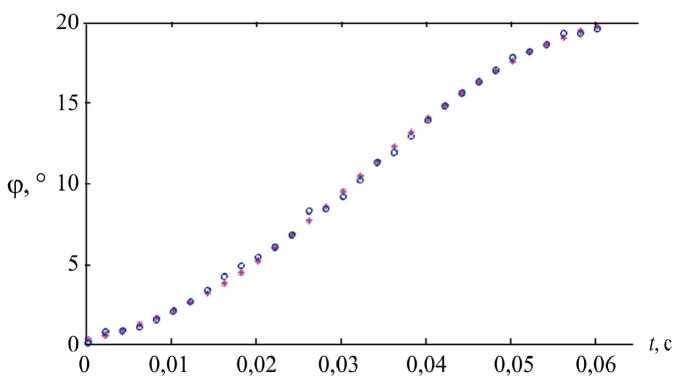
Рис. 2. Аппроксимация записи саккады функцией Больцмана

В результате применения метода наименьших квадратов для каждой записи саккады были построены оценки значений коэффициентов функции Больцмана. Далее выражения вида (1) были дважды продифференцированы, чтобы получить оценки угловых скоростей и ускорений глаза во время саккады (рис. 3).

Вязкоупругие модели мышцы

В литературе описано значительное число математических моделей мышечного сокращения; однако практически все они предложены для случаев изометрического или изотонического сокращения. Эти модели непригодны для случаев произвольного движения, в частности для моделирования саккады. Тем не менее существует ряд моделей, пригодных для описания произвольного движения мышцы.

Детальный обзор моделей мышцы приводится в работе Хилла [13]. Следует отметить, что в большинстве своем эти модели эквивалентны или вязкоупругой модели Фойхта, или модели Максвелла, кинематические схемы которых показаны на рис. 4. До настоящего времени практически нет никаких аргументов, позволяющих предпочесть одну из этих моделей.

В качестве примера приведем модель А.Г. Фельдмана [6], который предложил описывать силу F , развиваемую мышцей, законом

F = 4

- k ( l - X ) - gl при l -X> 0, 0 при l -X< 0.

Здесь l – текущая длина мышцы, k и g – коэффициенты, характеризующие упругие и вязкие свойства мышцы, X - управляющий параметр, имеющий смысл свободной длины мышцы.

Практически таким же образом моделируют силу, развиваемую глазодвигательной мышцей, M. Egerstedt и C. Martin [10]. Силы, развиваемые парой мышц-aнтагонистов, эти авторы описывают уравнениями

F =^- к ⁽ l - I 0 ) ^- gl + v, i = ^{1,2                          (3)}

вместе с необходимыми в этом случае дополняющими соотношениями v1 (t) • v2 (t) = 0, причем <

v 1 ( t ) ^ 0 при (p >  0, v ₂( t ) ^ 0 при (p <  0.

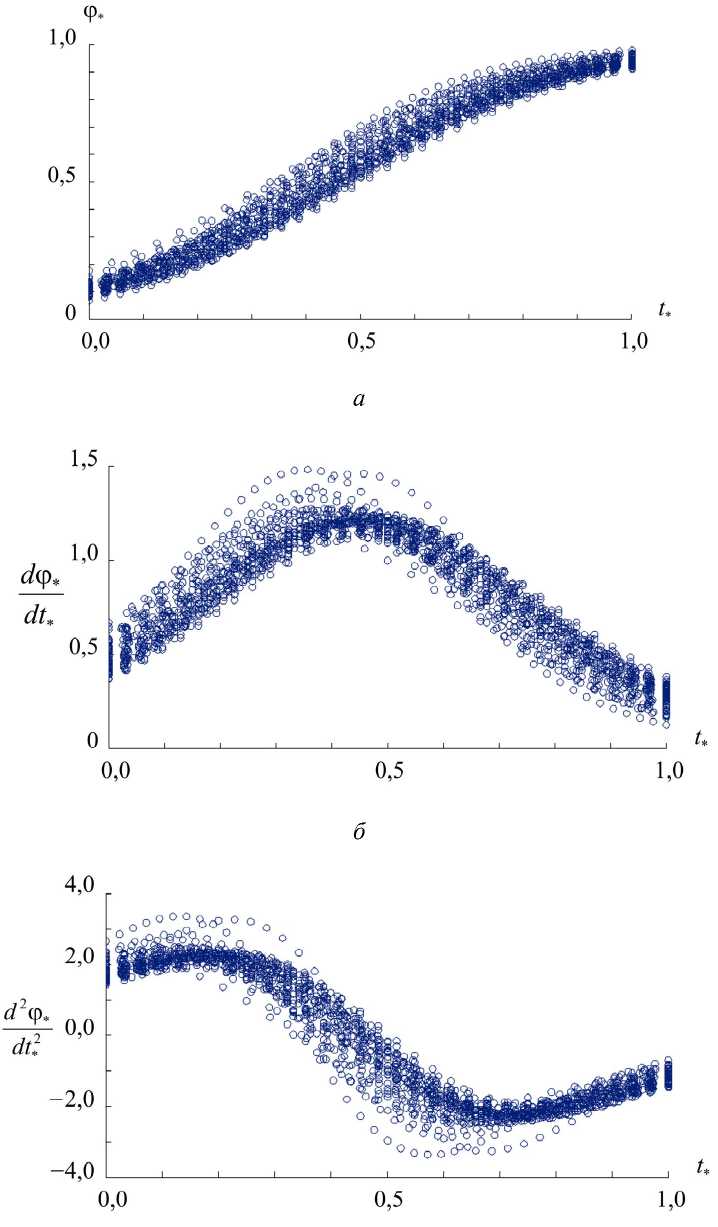
в

Рис. 3. Аппроксимации саккады функцией Больцмана. В безразмерных единицах показаны угол поворота глаза ( а ), вычисленные угловая скорость ( б ) и угловое ускорение ( в )

В этих уравнениях и соотношениях l0 - свободная длина мышцы, ф - угловая скорость глаза, v1 и v2 – управляющие параметры, имеющие размерность силы.

Программирование саккады

Подготовка и выполнение саккад определяются скоординированной работой многих структур головного мозга, включая стволовые структуры, подкорковые ядра и различные отделы коры больших полушарий (рис. 5). Вместе они составляют сложную систему, организованную по иерархическому принципу. Первые два уровня этой системы являются исполнительными, а вторые два – управляющими [3, 5].

Первый уровень саккадной системы выступает как единая эфферентная структура, обеспечивающая выполнение саккад. Он включает ядра черепно-мозговых нервов и наружные мышцы глаза, которые составляют три антагонистических пары [17].

Второй уровень объединяет стволовые структуры, получившие название стволового генератора саккад [15, 17]. Здесь выделяют два центра, управляющие горизонтальными и вертикальными движениями глаз, которые расположены в ретикулярной формации моста и среднего мозга. Структуры второго уровня управляют координацией движений обоих глаз. Их задача состоит в непосредственном запуске саккад с различных входов (верхнее двухолмие, кора больших полушарий, вестибулярный вход и пр.).

К третьему уровню относят верхнее двухолмие, базальные ганглии и ряд других структур, контролирующих работу стволового генератора саккад [12]. Ключевую роль среди структур этого уровня играет верхнее двухолмие, обеспечивающее перекодирование результата сенсорного описания внешнего мира на «язык» двигательных программ [5]. Нейроны нижних слоев верхнего двухолмия получают возбуждающие проекции от многих областей коры больших полушарий, принимают участие в процессах вычисления параметров саккады и обеспечивают основной выход зрительной системы на стволовой генератор саккад [11, 12, 17].

К четвертому уровню саккадной системы относят различные зоны коры больших полушарий, среди которых ключевую роль играют фронтальное глазодвигательное поле, заднетеменные и затылочные области [11, 12]. Структуры этого уровня принимают участие в интеграции высших когнитивных функций (внимания, памяти и принятия решения), связанных с процессами подготовки саккадических движений.

Уравнение движения. Дополняющее предположение. Синергия мышц

Запишем уравнение движения глаза для случая поворота вокруг вертикальной оси. Поворот глаза в этом случае осуществляется внутренней и наружной прямыми мышцами. Глаз будем считать твердым однородным шаром массы m и радиуса R , центр вращения которого совпадает с его геометрическим центром. Глазодвигательные мышцы прикрепляются к глазному яблоку в точках A и C , к сухожильному кольцу в точках B и D (рис. 6). Мышцы, изображаемые кривыми AB и CD , расположены в горизонтальной плоскости, проходящей через центр шара. Будем предполагать, что при рассматриваемых поворотах глаза экстраокулярные мышцы своими передними концами остаются «намотанными» на поверхность глаза. Это предположение позволяет выразить текущую длину мышцы в зависимости от угла поворота глаза ф :

l i (t ) = l 0 - R ф ( t ), 1 ₂( t ) = 1 0 + R ф ( t ). (5)

Уравнение движения глаза выражается законом изменения кинетического момента

Iф = Mz , где I - момент инерции глаза относительно оси вращения, I = -2 mR2; ф - угол поворота глаза, Mz – сумма моментов сил, развиваемых мышцами. Обозначая силы, развиваемые мышцами, через F1 и F2 соответственно, запишем уравнение движения в виде

I ф = R ( F 1 - F 2). (6)

Для каждой мышцы величину развиваемой силы считаем положительной, если она является тянущей. Обратим внимание на то, что в уравнениях (2) и (3) принято противоположное соглашение для знака силы.

Г.В. Коренев [2] выполнил анализ и разработку программ движения частей тела человека, в том числе и глаза. При программировании движения глаза, как и других кинематических цепей, обнаруживается неполнота этой программы. В качестве возможного пути разрешения проблемы неполноты программы Г.В. Коренев сформулировал принцип дополнения: «если программа не полна, то всегда можно поставить дополнительные цели таким образом, чтобы получить полную программу».

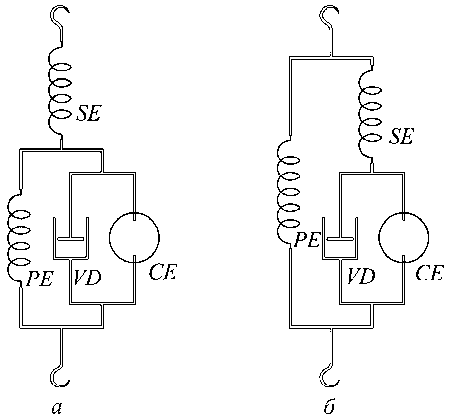
Рис. 4. Эквивалентные схемы вязкоупругой модели мышцы: а – модель Фойхта, б – модель Максвелла; PE и SE – параллельный и последовательный упругие элементы, CE – сократительный элемент, VD – вязкий демпфер

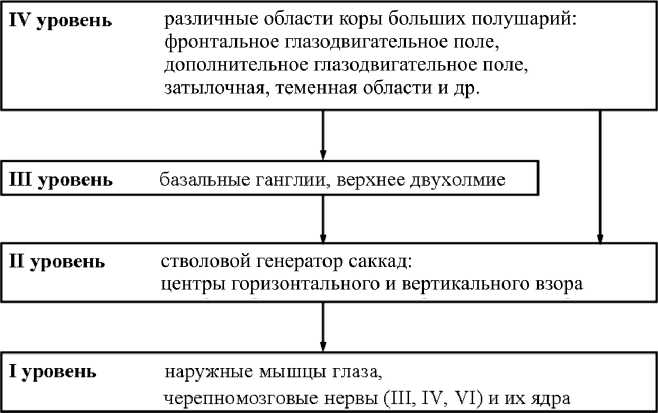
Рис. 5. Иерархический принцип строения саккадной системы

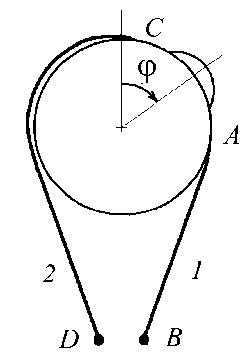
Рис. 6. Правый глаз, вид сверху: 1 и 2 – внешняя и внутренняя прямые экстраокулярные мышцы

Как уже отмечалось ранее, многие авторы, принимая вязкоупругую модель мышечного сокращения, делают различные допущения для доопределения программы движения. Рассматривая подход А.Г. Фельдмана к построению мышечного движения, приходим к заключению, что саккадическое движение строится как баллистическое с постоянным значением управления X . Такое допущение плохо согласуется с тем, что начальная и конечная фазы саккады обладают симметрией с достаточно высокой степенью точности. Дополняющее предположение в уравнении (2) означает, что поворот глаза осуществляется только одной мышцей.

Не выдерживает критики и дополняющее предположение (4), использованное в работе [10]. Поскольку угловая скорость глаза не меняет знака во все время саккады, получаем, что в модели этих авторов саккада совершается усилиями одной мышцы, тогда как мышца-антагонист создает только вязкоупругое сопротивление повороту глаза.

Сделаем иное дополняющее предположение. По оценке В.А. Филина [7], в течение недели глаз человека совершает более 400 тысяч саккад и после каждой из них поступает корректирующий эфферентный сигнал для глазодвигательных мышц. В силу огромного числа повторений движения вырабатывается двигательный навык. Н.А. Бернштейн [1] писал о высокой синергичности движений, осуществляемых на уровне штампов. Отметим также тот факт, что в состоянии покоя мышца не расслаблена полностью, а демонстрирует некоторый тонический уровень напряжения. Следовательно, при движении, требующем растяжения мышцы, можно говорить о дополнительном расслаблении этой мышцы так, чтобы она не создавала сопротивления движению. Другими словами, будем предполагать, что мышца-антагонист является фактически во время саккады мышцей-синергистом, расслабляясь соответствующим образом, а в надлежащий момент происходит мгновенная смена ролей мышц. Это предположение хорошо согласуется с изменением активности нейронов, иннервирующих глазодвигательные мышцы [17], и с электромиографическими записями [14] мышечной активности при саккаде.

Будем считать, что в уравнениях для мышечного усилия

F = k ( l - l 0 ) + gl + v , i = 1,2, (7) управление v строится как сумма четырех составляющих: тонической v _т , статической v _с , кинематической v _к и динамической v _д :

v = v т ⁺ v с ⁺ v к ⁺ v д . ⁽⁸⁾

Для каждой глазодвигательной мышцы все эти составляющие определяются независимо и вычисляются однозначно по текущим значениям угла, скорости и ускорения поворота глаза. Тоническая составляющая постоянна и принимается равной некоторой доле от максимальной силы, развиваемой мышцей,

• ^V 1т = v 2т = ^ v max , Ц = const.

Статическая компонента управления каждой мышцы находится из условия, что в стационарном положении, определяемом углом ф , при нулевых угловых скорости и ускорении глаза сила, действующая со стороны каждой мышцы (не считая тонической компоненты), равняется нулю:

F,= к (1(Ф) -10) + vfc = 0, i = 1,2, откуда с учетом соотношений (5) получаем выражения для статических компонент управления

• ^v 1c = kR Ф , v 2c = — ^kR ф .

Кинематическую компоненту управления каждой мышцы находим аналогично из условия, что при движении глаза с постоянной угловой скоростью мышца развивает такую кинематическую составляющую силы, что полностью компенсирует свое вязкое сопротивление:

gli+ Vk = 0, i = 1,2, откуда получаем выражение для кинематических компонент управления

• ^V 1k = g^{R ф} , v 2k = — g^{R ф} .

Наконец, динамические составляющие определяются в зависимости от знака программного углового ускорения глаза ф . Будем считать, что для динамических компонент имеет место условие, аналогичное условию (4):

^V 1д ⁽ t ) • v 2д ⁽ t ) = ⁰, причем

^V 1д ⁽ t ) * ⁰

_ v 2д ⁽ t ) * ⁰

при ф >  0, при ф <  0,

т.е. отлична от нуля лишь та динамическая компонента, для которой знак соответствующего момента силы совпадает со знаком углового ускорения глаза. Для ненулевой компоненты получаем выражение через программное угловое ускорение vi( t) = ^ vmax

-

( - 1) i R kA 1 V

-

^kA 2 + gA 2 z ⁽ t ) — ¹

z ( t )     D z ²( t ) )

_ . 4 mRA₂ z ( t ) - 1 + 5 ( i , t )----—

5 D ² z ²( t )

( 1     1 ^

V z ( t ) - 2 , ,

где обозначено: z(t) = 1 + e D и 5(i,t) = ((i = 1) = (t < B)). Этот закон управления вместе с уравнениями (5), (6) и (7) полностью задает программное движение глаза при саккаде.

Численный пример

Для саккады, задаваемой уравнением (1), было проведено покомпонентное вычисление управлений для обеих глазодвигательных мышц. В таблице приведены числовые значения коэффициентов, использованные для расчетов.

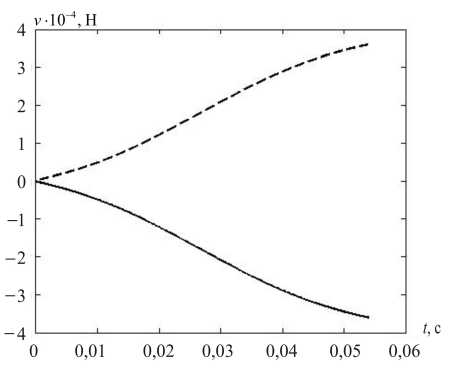
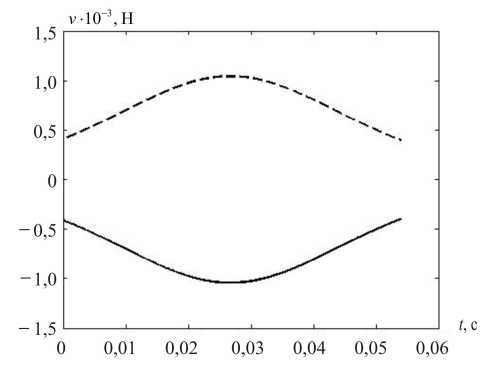
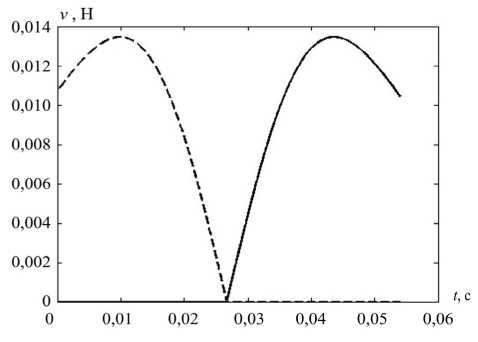
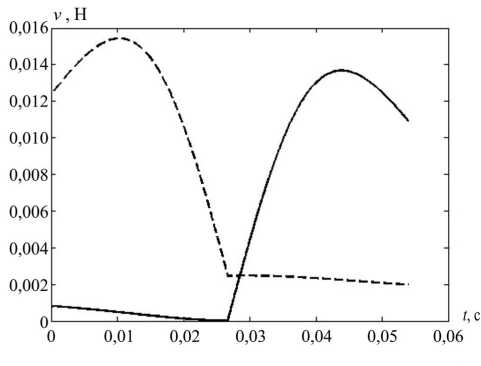
На рис. 7 показаны вычисленные значения компонент управлений (кроме постоянной, тонической) и их композиция – суммарные управления v ₁ и v ₂ .

б

в

г

Рис. 7. Компоненты мышечного управления при саккаде: а – статическая, б – кинематическая, в – динамическая, г – суммарное управление; v 1 – пунктирная, v 2 – сплошная линия

Числовые значения коэффициентов

Параметр	Значение	Размерность	Параметр	Значение	Размерность
A 1	0,376	рад	k	0,0856	Н / м
A 2	0,421	рад	g	0,0342	Н·с / м
B	0,0267	с	m	0,0107	кг
D	0,0128	с	R	0,0127	м
T	0,06	с	μ	0,05	—
l 0	0,03	м	V max	0,0245	Н

Выводы

В результате анализа экспериментальных данных показано, что с высокой точностью закон движения глаза во время саккады можно аппроксимировать функцией Больцмана. Такое аналитическое приближение позволяет находить угловые скорости и ускорения глаза дифференцированием функции Больцмана, а не исходных данных, содержащих значительный высокочастотный шум.

Принятые в работе дополняющие предположения о выборе закона управления мышцей в виде композиции четырех компонент и о том, что из двух динамических составляющих отлична от нуля лишь та, которая создает момент, совпадающий по знаку с угловым ускорением глаза, дают возможность полностью доопределить программу движения глаза и найти управляющие воздействия. Такой способ построения закона управления может быть использован для математического моделирования динамики глазодвигательного аппарата при саккаде.

Благодарности

Работа выполнена при поддержке РФФИ (грант 09–01–00809).