Концепция и методы обеспечения надежности мобильной техники при проектировании

Обеспечение конкурентоспособности изделий отечественного машиностроения непосредственно связано с необходимостью повышения уровня научно-технического сопровождения инновационных проектов. В значительной мере это относится к вопросам обеспечения прочностной надежности машин, которая закладывается в процессе выполнения рабочих проектов. Как показывает практика, в большинстве случаев инженерные расчеты ограничиваются определением максимальных напряжений от действия предельных нагрузок и затем путем их сопоставления с характеристиками статической прочности материалов оцениваются коэффициенты запаса ответственных деталей проектируемой конструкции. Очевидно, такой подход ограничивает возможность предсказания усталостных, износовых, термомеханических и других видов повреждений, которые, как показывает опыт, преимущественно являются причиной отказов тяжелонагружен-ных элементов машин. С другой стороны, следует отметить, что предусмотренные техническими заданиями сертификационные характеристики надежности изделий выявляются лишь путем анализа статистической информации, получаемой при эксплуатации серийной продукции.

Применение современных достижений в областях исследований динамики машин, прочности конструкций и вычислительных технологий позволяет принципиально изменить подход к прогнозированию и управлению надежностью изделий путем широкого и опережающего применения методов математического моделирования задач динамики и прочности машин. Постановка задачи прогнозирования прочностной надежности предусматривает последовательное выполнение следующих этапов:

• - описание многофакторного случайного воздействия внешней среды на рабочие органы и динамическую систему проектируемых изделий (ветровая нагрузка на высотные сооружения, воздействие профилей дорог на ходовую часть мобильных машин, воздействие со стороны грунта на рабочие органы дорожно-строительной техники т. п.);

• - компьютерное моделирование процессов реальной эксплуатации машин;

• - определение статистических характеристик силового и кинематического взаимодействия элементов конструкции;

• - конечно-элементное моделирование полей напряженно-деформированного состояния с целью выявления потенциально опасных зон ответственных деталей;

• - моделирование процессов формирования усталостных, износовых, термомеханических и других видов отказов с учетом случайного характера нагружения и рассеяния прочностных свойств применяемых материалов;

• - определение количественных характеристик надежности, таких как функция вероятностей безотказной работы, средняя наработка до отказа, гамма-процентный ресурс тяжелонагруженных элементов машин и т. п.;

• - корректировка исходных данных проекта по динамическим свойствам проектируемых изделий и прочностным характеристикам деталей с целью обеспечения требуемых показателей надежности.

Комплекс названных исследований представляет собой инженерную методику имитационного моделирования испытаний. К числу наиболее значимых преимуществ подхода следует отнести возможность проведения параметрического прогноза и количественной оценки влияния характеристик проектируемой машины на эксплуатационную нагруженность и долговечность ответственных элементов. Его применение также позволит повысить эффективность проведения стендовой отработки тяжелонагруженных узлов и обосновать программу натурных испытаний опытных образцов машин.

Предлагаемое исследование иллюстрирует реализацию метода имитационного моделирования испытаний на примере тяжелонагруженных элементов ходовой системы быстроходных гусеничных машин, предназначенных для эксплуатации в условиях необустроенной местности (рис. 1). Актуальность задачи обусловлена тем, что надежность таких машин в значительной степени определяется долговечностью гусеничного движителя, работающего в весьма тяжелых условиях.

Одним из основных элементов рассматриваемой методики является математическая модель гусеничной машины. Применяемые в настоящее время математические модели шасси гусеничной машины можно разделить на несколько групп.

Модели, предназначенные для исследования плавности хода, достаточно подробно описывают подрессоренный корпус. При этом обычно рассматривается только режим прямолинейного движения, силовая установка моделируется одним инерционным элементом [1–3].

Математические модели, ориентированные на исследование динамики силовой установки, отличаются подробным описанием трансмиссии и двигателя машины, при этом подрессоренный корпус описывается достаточно приближенно [4, 5].

При исследовании процессов криволинейного движения уделяется большое внимание описанию взаимодействия гусеницы и грунта, а также работе механизма поворота; корпус машины при этом обычно рассматривается как тело, совершающее плоское движение [6–9].

Для реализации методики имитационного моделирования испытаний предложена математическая модель, ориентированная на решение задач прочностной надежности ходовой части гусеничной машины. Модель характеризуется следующими отличительными особенностями:

• – модель описывает динамику связанной нелинейной системы «грунт – гусеница – подрессоренный корпус – силовая установка – водитель»;

• – учитывает существенные нелинейности системы, такие, как односторонние связи в гусеничном обводе и опорных катков с грунтом, нелинейные характеристики двигателя, фрикционных элементов и гидромеханических передач;

• – отображает изменение структуры силовой установки при переключении передач и работе механизма поворота;

• – учитывает варьирование скорости в широком интервале значений при движении машины по труднопроходимой местности [10];

• – для расчета сил сопротивления повороту использовано конечно-элементное моделирование взаимодействия траков гусеницы с грунтом, что позволяет учитывать особенности формы опорной поверхности траков, моделировать процессы погружения трака и нагребания грунта [11, 12].

Предложенную модель можно условно рассматривать как совокупность связанных частей:

• – основной подсистемы, описывающей динамику подрессоренного корпуса машины;

• – модуля для расчета сил взаимодействия опорной поверхности гусеницы с грунтом при прямолинейном и криволинейном движениях;

• – подсистемы, описывающей динамику силовой установки машины;

• – технико-эргономической подсистемы, описывающей работу механика-водителя по приведению скорости движения машины в соответствие с дорожной ситуацией.

Схема подсистемы, моделирующей подрессоренный корпус машины, представлена на рис. 2,

• 3, а. Корпус рассматривается как твердое тело, имеющее шесть степеней свободы. С центром тяжести корпуса о связана подвижная система координат o – x – y – z . Положение на местности рассматривается в неподвижной системе O 1 – X – Y – Z . В качестве обобщенных координат приняты координаты центра тяжести корпуса в неподвижной системе X , Y , Z , углы продольно- и поперечноугловых колебаний 9, в , а также угол поворота относительно вертикальной оси а( рис. 3, а). Корпус имеет массу m к и моменты инерции I x , I y , I z относительно соответствующих осей.

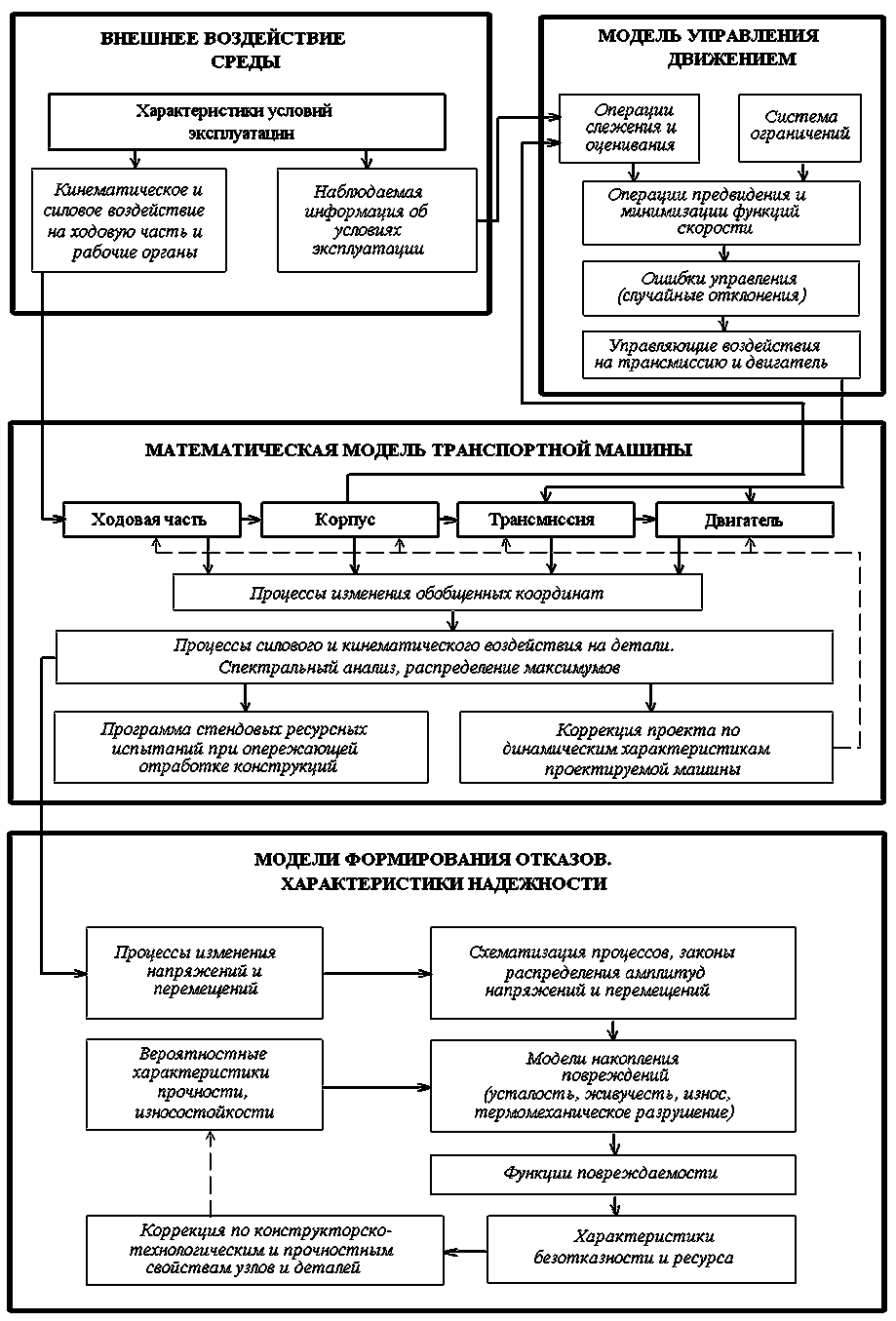
Рис. 1. Блок-схема комплексного моделирования

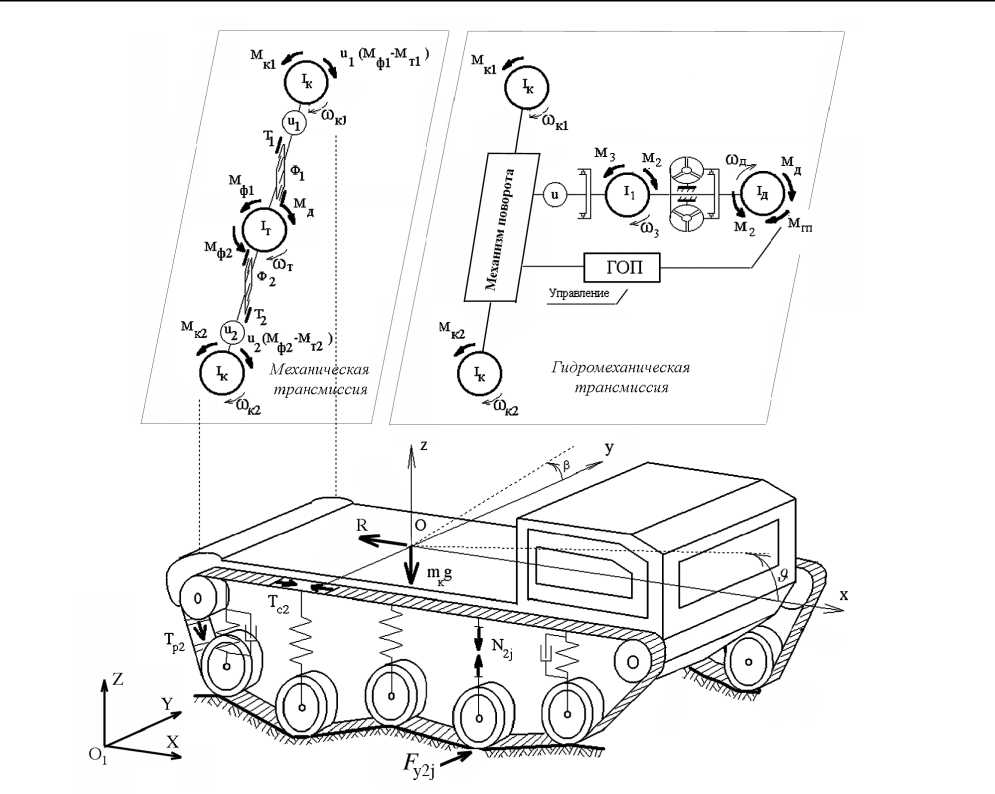
Рис. 2. Расчетные схемы гусеничного движителя, подрессоренного корпуса и силовой установки

На корпус машины действуют сила веса m к g , вертикальные усилия со стороны подвесок N ij ( i = 1...2 – номер борта, j = 1... n – номер подвески), силы натяжения рабочих и своб о дных ветвей гусениц T p i , T c i , а также сила сопротивления пря м олинейному движению R . При дв и жении по криволинейным участкам трассы на опорные катк и машины действуют нагрузки F yij , которые через балансиры подвески также передаются на корп у с машины.

Подвески машины моделируются эквивалентными вертикальными упругими и демпфирующими элементами с нелинейными характеристиками. При этом учитываются отрыв ы опорных катков и пробои подвесок на упорах. При движен и и без отрыва вертикальная координата оси опорного катка принимается равной высоте микро п рофиля трассы в соответствую щ ей точке. В случае отрыва соответствующая координата рассчитывается путем интегрирования уравнения движения массы катка. Наряду с усилиями со стороны подвесок на крайние катки действуют усилия со стороны гусениц: T c i , T p i . Гусеничные ленты моделируются нелинейными упругими элементами одностороннего действия.

При моделировании криволинейного движения м ашины важной задачей является адекватное определение сил сопротивления, действующих на опорные поверхности гусениц. Для и х расчета в настоящее время используется несколько принцип и ально разных подходов.

Первая группа методов предполагает расчет момента сопротивления повороту и б о ковой силы в зависимости от свойств грунта, радиуса и с м ещения центра поворота по эмп и рическим формулам [13, 14]. Опыт исследований показывает , что результаты расчета с испо л ьзованием такой модели удовлетворительно согласуются с результатами испытаний тихоходных м ашин.

Другой подход основан на использовании математической теории трения [7, 15]; при этом силы взаимодействия гусеницы с грунтом рассматриваются как нагрузка, распределенная по опорной поверхности. Очевидно, что такой метод позволяет получить а д екватные р езультаты в случае движения машины по жесткой, практически недеформируемой поверхности.

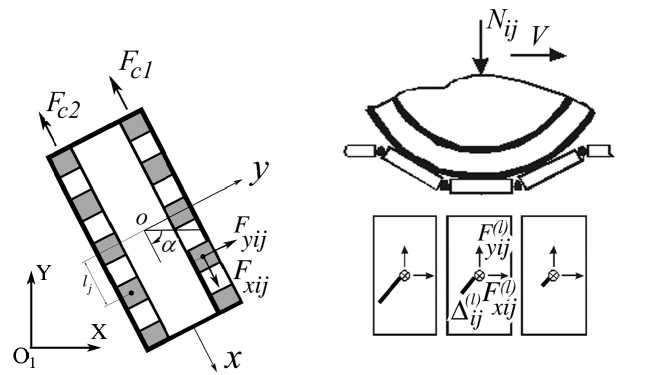
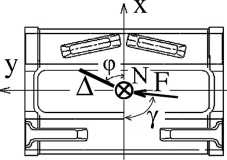
В предлагаемой математической модели гусеничной машины использован принципиально иной подход для описания взаимодействия гусеницы с грунтом [6, 8]. В его основу поло ж ено экспериментально обоснованное допущение о том, что взаимодействие с грунтом происходит на так называемых «активных» участках, находящихся в окрестности опорных катков машины. П ри этом распределенную по длине гусеницы нагрузку заменяют сосредоточенными силами, действующими на активных участках F xij и F yij ( i = 1, 2 – номер борта машины, j – номер опор н ого катка, рис. 3, а). Использование такого подхода позволяет учесть реальное распределение вертикальных нагрузок по длине опорной ветви, совместно рассматривать продольное и поперечн о е проскальзывание, а также определять поперечные нагрузки, действующие на каждый опорный каток машины.

а)                                                б)

Рис. 3. Нагрузки, действующие на опорную поверхность (а); нагрузки и перемещения на активном участке (б)

Силы F xij и F yij формируются как сумма нагрузок F _x ⁽ _i ^l _j ⁾ , F _y ⁽ _i ^l _j ⁾ ( l – номер т р ака), дейс т вующих на траки в активном участке. Распределение нагрузок F _x ⁽ _i ^l _j ⁾ , F _y ⁽ _i ^l _j ⁾ , а также смещения тра к ов Δ _i ⁽ _j ^{l )} схематично показаны на рис. 3, б. Смещения Δ _i ⁽ _j ^{l )} могут быть вычислены путем интегрирования по времени скорости проскальзывания трака относит е льно грунта за время прохождения актив- ( l )        ( l )

ного участка. В предлагаемой модели нагрузки F _xij , F _yij рассчитывают в зависимости о т катковой нагрузки и смещения Δ _i ⁽ _j ^{l )} с помощью соотношений, полученных по результатам конечноэлементного расчета процесса взаимодействия трака и грунта [12]. В настоящее время метод конечных элементов широко используется для моделирования взаимод е йствия с грунтом движителей и рабочих органов машин различного назначения [16, 17]; его применение позволяет учесть характеристики деформируемого грунта и форму опорной поверхности траков, а также адекватно описать процессы их взаимодействия, сопровождающиеся большими перемещениями. Для моделирования применен пакет программ LS-DYNA [11], предназначенный для м о делирования процессов, сопровождающихся большими д е формациями и разрушением м а териала. В расчетах использована модель материала FHWA-SOIL (*MAT_147), специально пред н азначенная для описания грунта. Свойства материала задавались на основе справочн ы х данных.

На первом этапе были проведены тестовые расчеты взаимодействия с грунтом одиночного трака быстроходной машины (БМП-2). Конечноэлементные модели трака и грунта показаны на рис. 4, а; при этом гребни трака, не взаимодействую щ ие с грунтом, не моделировались. В процессе расчетов трак нагружался вертикальной силой N и после погружения сдвигался в плоскости грунта в заданном направлении на заданное расс т ояние (рис. 4, б). В результате получены зависимости полной сдвигающей нагрузки ( F ), а такж е ее продольной ( F x ) и поперечной ( F y ) составляющих от соответствующих перемещений.

Выполнен большой объем расчетных исследований для различных видов грунт а , траков с грунтозацепами разной высоты и формы, а также для разнообразных режимов наг р ужения.

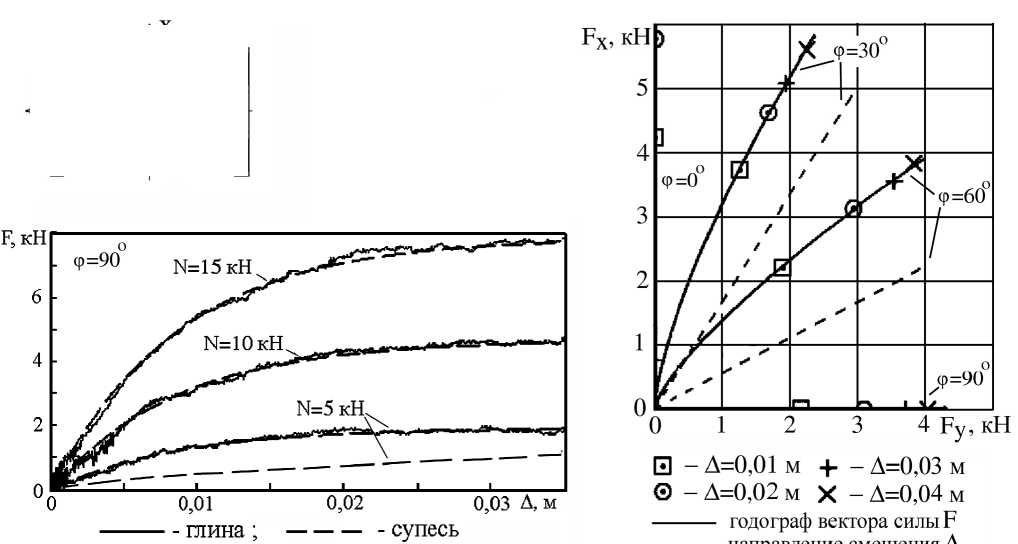
В качестве примера на рис. 5, а приведены зависимости силы F от смещения А при сдвиге трака в поперечном направлении на плотном грунте (глина, ц елина), а также на мягком (супесь) для различных значений вертикальной нагрузки N . Эти результаты демонстрируют увеличение F при увеличении N. Для мягкого грунта (супесь) сдвигающая нагрузка существенно мень ш е, чем для плотного при той же нормальной нагрузке.

Нормальная нагрузка

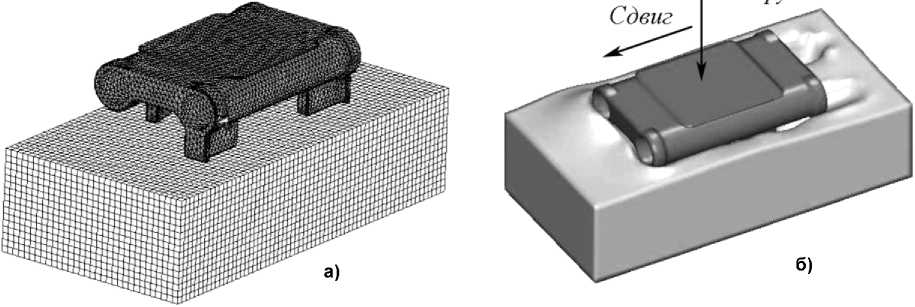
Рис. 4. Конечноэлементная модель трака и фрагмента грунта (а); деформированное состояние грунта при перемещении трака (б)

На рис. 5, б изображены зависимости продольной составляющей нагрузки F x от поперечной F y при сдвиге трака в различных направлениях ( N = 10 кН); направление сдвига отмечено пунктирной линией. Эти результаты показывают, что направление силы взаимодействия трака с грунтом не совпадает с направлением перемещения. По мере сдвига трака угол между направлением силы и перемещением изменяется.

На основании анализа результатов расчетов получена аппроксимирующая зависи м ость, связывающая силу, сдвигающую трак в плоскости дороги F , с перемещением А и вертикальной нагрузкой:

F = ( N / N о ) m ^{( ф )} F m ( ф ) [ 1 - exp( - c ( ф ) А ) ] , где N 0 — среднее значение вертикальной нагрузки, действующей на трак; ф — угол меж д у направлением перемещения и продольной осью трака.

б)

а)

Рис. 5. Зависимости силы от перемещения при боковом сдвиге трака (а); зависимости сдвигающей нагрузки от величины и направления сдвига (б)

Также предложена зависимость, связывающая угол между сдвигающей силой и продольной осью трака γ с углом φ:

γ= a 1 + a 2 ϕ+ a 3 ϕ 2 .

Функции m (φ), F m (φ), c (φ) и постоянные коэффициенты a 1, a 2, a 3 получены для разных видов грунта и траков с различными грунтозацепами.

В дальнейшем данные соотношения использованы в математической модели гусеничной машины для расчета сил, действующих на опорную поверхность гусеницы.

Одной из подсистем рассматриваемой математической модели является математическая модель силовой установки. В связи с разнообразием применяемых двигателей, трансмиссий и механизмов поворота, структура этой части модели должна определяться особенностями рассматриваемой машины. Поскольку модель машины ориентирована на исследование низкочастотной динамики, признано целесообразным не включать в ее состав упругие элементы. Однако для адекватного описания переходных режимов (переключение передач, изменение подачи топлива, работа механизма поворота) она должна содержать инерционные элементы, элементы, моделирующие работу фрикционов, гидрообъемных и гидродинамических передач, а также учитывать характеристику двигателя. Модель машины с механической трансмиссией представлена в [18].

Для предлагаемой математической модели получены дифференциальные уравнения движения. В качестве примера приводятся дифференциальные уравнения, описывающие движение основной подсистемы модели (подрессоренного корпуса):

X = x cos a + y sin a ,     Y = y cos a + x sin a ,

• 2                                                 2 n

m К ⁽ x + ^u z + a y ) = E (T pi - T_c i - F i ) - R , m *^{( y} -^e z -a x ) = EE F yij , i = 1                                                                  i = 1 j = 1

• *                       2 n

^m * (z ^{- U} x ^{+ в} y ) = E ⁽ E N i , j — T c i sin V c ^{+ T} pi sin V p ) ^{- m} к g, i = 1 j = 1

2 n

Iy 9 + ae(Iz - Ix ) = E (E Ni, jlj + TPi (Lb sin Vp - Hb cos Vp + Ho ) - i=1 j=1

- T _{c i} ( L _нsin ψ _c - H_b cos ψ _c + H_o ) - F _{c i}H_o ) + M _{c y} ,

n

Ixe + a0(Iy -Iz) = 0,5B(E(Ni,j — N2,j) + sinVp(Tp2 — Tpi) + sinVe(Tc2 — Tei)), j=1

2 n

Iz0. + p0(Ix - Iy) = 0,5B(Tpi - Tp2 + Tc2 - Tei + Fc2 — Fei) — EEljFyj , i=1 j=1

где H o , H b – высота над опорной поверхностью центра тяжести машины и оси ведущего колеса; L_b , L _н – расстояние вдоль продольной оси от центра тяжести машины до осей ведущего и направляющего колес; l j – продольная координата j -го активного участка.

При расчете нагрузок, действующих на активный участок, а также натяжения ветвей гусениц используется значение скорости проскальзывания опорных поверхностей i- го борта машины относительно грунта в продольном направлении v p _i ( t ) . Эта величина определяется на каждом шаге интегрирования уравнений движения на основе равновесия гусеничного обвода, в соответствии с которым разность усилий в рабочей ( T p i ). и свободной ( T ci ) ветвях гусеницы должна равняться сумме продольных усилий, действующих на активных участках ( F xii ) (рис. 6).

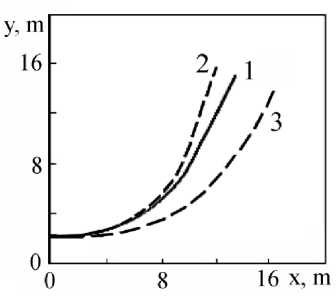
Для численного интегрирования уравнений движения разработан специальный пакет программ, с помощью которого выполнена серия тестовых расчетов. Анализ результатов и их сопоставление с экспериментальными данными подтверждает адекватность предложенной математической модели. В качестве примера на рис. 7. представлены траектории движения машины (БМП-2) при повороте с фиксированным радиусом на различном грунте (супесь и плотная глина). Расчеты выполнены для машины со стандартными траками гусениц (1, 2) и с изношенными грунтозацепами (3). В случае изношенных грунтозацепов, а также на мягком грунте радиус поворота получился больше, чем на жестком грунте. Это объясняется меньшим сопротивлением заносу и большим проскальзыванием опорной поверхности относительно грунта.

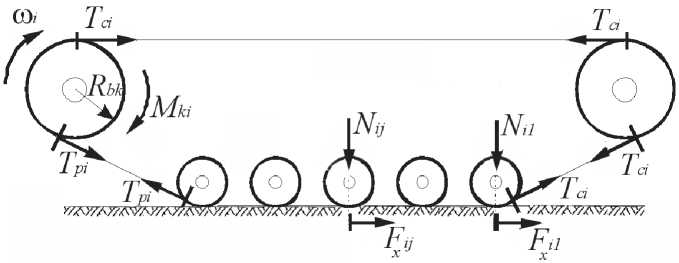
Рис. 6. Нагрузки в гусеничном обводе

Таким образом, применение в составе математической модели гусеничной машины предлагае- мой методики расчета сил взаимодействия траков гусеницы с грунтом позволяет получить процес- сы изменения нагрузок, действующих на элементы ходовой части при движении машины по трассе, а также кинематические параметры криволинейного движения с учетом формы опорной поверхности траков и свойств грунта. Процессы изменения нагрузок в дальнейшем используются для расчетной оценки долговечности элементов движителя. Анализ кинематических параметров поворота может быть использован при оценке управляемости машины в различных условиях.

В математическую модель транспортной машины включена подсистема, имитирующая действия водителя по корректировке скорости движения. Скорость движения по местности задается в виде функции пути, зависящей от условий эксплуатации и динамических характеристик проектируемой машины, с одной стороны, и ряда технических и эргономических ограничений – с другой.

Рис. 7. Траектории поворота машины с фиксированным радиусом: 1 – грунт – супесь; 2 – грунт – плотная глина, стандартный трак; 3 – грунт – супесь, трак с изношенными грунтозацепами

При реализации предлагаемой методики для моделирования движения машины по трассе необходимо задание комплекса факторов внешнего воздействия, к которым, в частности, относятся микро- и макропрофиль трассы, радиусы и протяженности криволинейных участков, характеристики одиночных препятствий, характеристики грунта и др. Для задания этих параметров удобно использовать картографические описания трасс известных испытательных станций и полигонов, которыми располагают отрасли-производители сельскохозяйственной, автомобильной, дорожностроительной и другой инженерной техники.

Результаты расчетных исследований, выполненных с помощью предлагаемой математической модели, а также примеры практического применения предлагаемой методики будут представлены в следующей публикации.