Конечно-амплитудные возмущения адвективных течений в горизонтальном слое несжимаемой жидкости со свободной верхней границей при слабом вращении
Автор: Кочинов Алексей Юрьевич, Шварц Константин Григорьевич
Журнал: Вычислительная механика сплошных сред @journal-icmm
Статья в выпуске: 2 т.8, 2015 года.
Бесплатный доступ
Изучается поведение пространственных конечно-амплитудных возмущений адвективного течения во вращающемся горизонтальном слое несжимаемой жидкости со свободной верхней и твердой нижней границами при слабом вращении. Исследование проводится в декартовой системе координат на основе уравнений конвекции в приближении Буссинеска во вращающейся системе отсчета. В силу сложности трехмерной постановки обсуждаются только предельные случаи: пространственные винтовые периодические по x возмущения в виде валов с осью, перпендикулярной оси x, и пространственные спиральные периодические по y возмущения в виде валов с осью, параллельной оси x. При фиксированном числе Прандтля (Pr=6,7) построены изолинии возмущений при различных значениях чисел Тейлора и Грасгофа. Поведение конечно-амплитудных возмущений рассматривается за порогом устойчивости. Нелинейная задача решена численно, с помощью метода сеток. Использовалась явная конечно-разностная схема с центральными разностями. Уравнение Пуассона для функции тока возмущений решалось методом последовательной верхней релаксации. Полученные результаты позволили оценить поведение возмущений, найти скоростные характеристики, амплитуду и период повторений возмущений. На основании анализа вычисленных данных установлено, что под воздействием температурной неоднородности в надкритической области зарождаются винтовые пространственные структуры (вихри), ориентированные поперек слоя. Возмущения температуры представляют собой систему чередующихся теплых и холодных пятен, расположенных в направлении градиента температуры на границах слоя. С ростом числа Тейлора вихри возле свободной верхней границы вытесняют вихри, находящиеся вдоль твердой нижней границы, амплитуда вихрей увеличивается. С ростом числа Грасгофа тепловые пятна перестраиваются, расширяются, при этом теплые из них локализуются у верхней и нижней границ слоя, а холодные - в центре слоя. Движение становится более сложным. Уменьшается временной период повторения картины конечно-амплитудных возмущений.
Адвективное течение, устойчивость, вращение, конечно-амплитудные возмущения, винтовые возмущения, спиральные возмущения
Короткий адрес: https://sciup.org/14320762
IDR: 14320762 | УДК: 532.51.013.4:536.252 | DOI: 10.7242/1999-6691/2015.8.2.15
Текст научной статьи Конечно-амплитудные возмущения адвективных течений в горизонтальном слое несжимаемой жидкости со свободной верхней границей при слабом вращении
Адвективными называют течения жидкости или газа, которые порождаются горизонтальным градиентом плотности в плоском горизонтальном слое жидкости, на границах которого температура линейно изменяется по продольной координате. При наличии вращения слоя такие течения впервые были аналитически описаны в [1–3]. Особенность течения заключается в том, что для него характерны обе горизонтальные компоненты скорости, но при этом отсутствует вертикальная компонента скорости; вектор скорости в потоке перпендикулярен силе плавучести. Во вращающемся слое адвективное течение имеет спиралевидную форму, наподобие изотермического течения Экмана [4–6].
Без учета вращения и при линейном изменении температуры на обеих границах адвективное течение впервые изучалось в [7]. Для случая свободной верхней границы, а также твердых границ исследована устойчивость этого течения в [8–10].
Устойчивость адвективного течения во вращающемся слое жидкости с твердыми границами при Pr = 6,7 (вода) рассматривалась в [11-15]. Различные механизмы неустойчивости адвективных течений при твердых, свободных, теплоизолированных границах, а также границах с теплоотдачей представлены в монографии [6] и обзоре [16].
Формированию и колебательному поведению гидротермальных волн, а также критическим условиям их возникновения посвящена работа [17]. Экспериментальная установка представляла вращающийся мелкий кольцевой бассейн, в котором термокапиллярный поток нагревался на наружной стенке и охлаждался на внутренней.
В работе [18] численно исследовалось формирование вторичных потоков в адвективном течении над нагретой поверхностью в цилиндрическом слое. Показано, что над областью нагрева образуется пограничный слой, в котором возбуждаются вторичные течения в виде спиральных валов. В пакете гидродинамических расчетов Fluent построены двух- и трехмерная модели данного процесса. С помощью двухмерной модели найдены частоты, характеризующие формирование поперечных вторичных структур. В рамках трехмерной модели детально рассмотрена эволюция вторичных течений.
С точки зрения устойчивости течения по отношению к возмущениям различного типа авторы [19] анализировали стационарное адвективное течение в длинном горизонтальном канале прямоугольного сечения с твердыми адиабатическими границами при наличии однородного продольного градиента температуры. Определены зависимости критического числа Рэлея от числа Прандтля при различных размерах сторон поперечного сечения канала.
В [20] численно изучались трехмерные адвективные течения в горизонтальном цилиндре с квадратным поперечным сечением при условиях теплоизолированных боковых границ и наличии однородного продольного градиента температуры. Оказалось, что структура течения существенно обусловлена числом Грасгофа, длиной канала и числом Прандтля, и в зависимости от этих параметров течение может обладать различными видами симметрии и по-разному вести себя во времени. Установлено, что возможны варианты перехода к колебательным режимам течений: либо с предварительным нарушением симметрии течения (вилочная бифуркация), либо без смены вида симметрии. Также очерчена область параметров, в которой наблюдается лишь вилочная бифуркация, а колебательные режимы течения не возникают.
В работе [21] экспериментально исследовалась термокапиллярная конвекция бинарной смеси при умеренном числе Прандтля в неглубоком кольцевом бассейне, в котором в разных пропорциях нагревался наружный цилиндр и охлаждался внутренний цилиндр. Обнаружено, что в гидротермальных волнах двумерное стационарное течение и хаотические явления упорядочиваются с ростом числа Рейнольдса, а критическое число Рейнольдса уменьшается с увеличением пропорции и концентрации растворенного вещества в условиях эксперимента. Волновое число, угол распространения и фундаментальная (самая низкая) частота гидротермальных волн монотонно уменьшаются с увеличением пропорций растворенного вещества, а его концентрация незначительно влияет на эти характерные параметры гидротермальных волн.
Линейная устойчивость адвективного течения в горизонтальном слое жидкости со свободной верхней границей являлась предметом исследования в [22]. Найдено точное решение, которое описало аналитически этот тип течений. Расчеты горизонтальных компонент скорости выявили следующее: адвективное течение имеет спиралевидную структуру; пограничные слои формируются и на нижней, и на свободной верхней границах; профили компонент скорости и температуры зависят от числа Тейлора. Построены кривые для критического числа Грасгофа и волновых чисел в виде функций числа Тейлора. С помощью метода малых возмущений получена линейная система дифференциальных уравнений в частных производных. Численные расчеты, выполненные при фиксированном числе Прандтля (Pr = 6,7, вода), показали, что характерной является колебательная неустойчивость адвективного течения для любого значения числа Тейлора. Исследование позволило заключить, что вращение — это стабилизирующий фактор для адвективного течения в случае винтовых возмущений — второго типа пространственных помех. Для спиральных возмущений — первого типа пространственных помех, при малых и больших значениях числа Тейлора эффект от вращения также стабилизирующий. При умеренных числах Тейлора (42 < Ta < 1000 ) наблюдалась обратная тенденция. Обоснована рэлеевская неустойчивость. Установлено, что для спиральных возмущений имеет место одна критическая рэлеевская мода, для винтовых возмущений — две моды. Наконец, главный вывод о роли вращательного эффекта в сохранении устойчивости состоял в том, что первый тип пространственных возмущений более опасен, чем второй.
Интерес к течениям такого рода связан с их приложениями, прежде всего геофизическими: к динамике атмосферы и океана, переносу и диффузии примеси от антропогенных источников [22], а также другими: к некоторым технологическим процессам, в частности к перемешиванию жидкого металла, к техническим устройствам, например, установке для выращивания кристаллов по методу Чохральского [23].
Линейная теория, основанная на малых возмущениях, позволяет найти границу устойчивости основного плоскопараллельного конвективного течения. Поведение же возмущений конечной амплитуды в надкритической области может быть изучено лишь с использованием полных нелинейных уравнений конвекции [15].
Характер возмущений конечной амплитуды при наличии свободной верхней границы ранее не обсуждался. В монографии [6] рассмотрен случай только твердых границ.
Данная работа посвящена исследованию поведения конечно-амплитудных возмущений адвективного течения в горизонтальном слое несжимаемой жидкости со свободной верхней границей за порогом устойчивости, который определен в работе [22]. Задача решается в нелинейной постановке при слабом вращении (0 < Ta < 100).
-
2. Постановка задачи
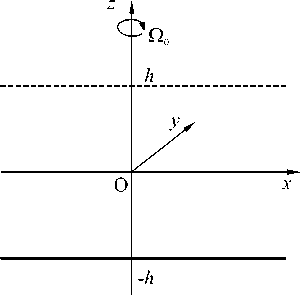
Рис. 1. Плоский горизонтальный слой жидкости, вращающийся с постоянной угловой скоростью Q o
Рассмотрим плоский горизонтальный слой несжимаемой жидкости со свободной верхней границей z = h , который ограничен снизу твердой плоскостью z = - h и вращается с постоянной угловой скоростью Q o. Ось вращения совпадает с вертикальной осью координат. На обеих границах задана температура, линейно меняющаяся по координате x ( T = Ax , где A — постоянный горизонтальный температурный градиент), и условие замкнутости потока:
„ dvd z = h : T = Ax, —- = 0 , —- = 0 v = 0;
dzd z = - h : T = Ax, v = 0 ,(1)
hh
J v x dz = 0, j vydz = 0 .
-
- h-
Для описания тепловой конвекции в слое воспользуемся уравнениями в приближении Буссинеска в декартовой системе координат с учетом вращающейся системы отсчета [24]. Положим, что число Фруда Fr = Q 0 l/g меньше единицы (здесь g — ускорение свободного падения, l — горизонтальный линейный масштаб), что позволяет пренебречь центробежной конвективной силой. Деформацию свободной поверхности, вызванную вращением и термокапиллярным эффектом, проигнорируем. Выбрав в качестве единиц измерения длины, времени, скорости, температуры и давления, соответственно, h , h 2/v, g в Ah 2 /v , Ah , p 0 g в Ah 2 (где v — кинематическая вязкость, в — коэффициент теплового расширения, р 0 — средняя плотность), получим уравнения в безразмерном виде:
dv
+ d t
Gr(vV) v + VTa (ez x v)
= -V P + A v + T e z ,
div v = 0,
= g в Ah4 v 2
d T 1 .T
+ Gr v V T = A T , d t Pr
Г 2Q0 h 2 )
Ta = 0
I v }
,
Pr = -.
X
где v ( t , x , y , z ) = ( v x , vy , vz ) — вектор скорости; T , P — отклонение температуры и давления от равновесных значений; e z ( 0,0,1) — орт-вектор вертикальной оси z ; Gr, Ta , Pr — числа Грасгофа, Тэйлора и Прандтля; X — коэффициент температуропроводности; Ra = GrPr — число Рэлея.
При граничных условиях (1) в плоском вращающемся слое несжимаемой жидкости формируется однородное по x , y стационарное адвективное течение, которое можно описать аналитически [6, 22] в следующем виде:
v x = u 0 ( z ) , v y = v 0 ( z ) , vz =0, T = T 0 ( x , z ) = x + T 0 ( z ) , P = P 0 ( x , У , z ) . (3)
Подставив соотношения (3) в систему уравнений (2), получим дифференциальные уравнения для распределений скорости, температуры и давления:
d po
"= = x + T 0, d z
-
- vtv v о =- p + u 0, d x
vtv u °dp+v;, dy
Ra u о = T 0.
Здесь и далее символ «'» означает дифференцирование функции по координате z . Граничные условия и условия замкнутости потока имеют вид:
z = 1: u 0 = 0, v‘ = 0, To = 0, z = -1: u 0 = 0, v 0 = 0, T0 = 0, (5)
j u 0 dz = 0, j v 0 dz = 0. - 1 - 1
С учетом граничных условий (5) найдем точное решение задачи (4) [6, 22]:
u 0 ( z ) = Re ( M ( z ) ) , v 0 ( z ) = Im ( M ( z ) ) ,
T
Ra
0 Fr"
Ta
v 0
( z ) - 2 v 0 ( 1 )( 1 + z ) + 2 (1 - z 2) Im f D 2 ц sh ( ц )
где
M (z) =
ch (ц( z-1)) ц2 D
sh ( ц ( z + 1 ) ) Ц 3 D
sh ( 2 ц ) 2 ц 3 D
+ ah^sh ( ц z ) + sh ( ц )) -а2 , lt lt
ц =
Ta
4т( 1 +i ) ,
i = V-l,
D = ' ''ch ( 2 ц ) , D 2 = - shW ch ( ^ > .
2 ц ц ц
Профили компонент скорости u 0 ( z ) , v 0 ( z ) и, соответственно, т 0 ( z ) антисимметричны относительно оси x . Они изображают движение типа спирали Экмана. Температура представляется в виде функции, описывающей два антисимметричных тепловых потока, направленных в противоположные стороны. С ростом числа Тейлора вблизи твердой границы образуются пограничные слои вихревых возмущений скорости и температуры.
Для исследования устойчивости стационарного адвективного течения во вращающемся слое жидкости применим метод малых возмущений [6, 12]:
v = V 0+ V , V 0 = ( u 0, v 0,0 ) , V = ( u , v , w ) , T = T 0 +9 , P = p 0 + "p , (7)
где V , 9 , p — возмущения скорости, температуры, давления.
Подставим выражения для возмущенных полей (7) в исходную систему (2) и граничные условия (1), учитывая (5):
^ V + Gr [ ( V V ) V + ( V V ) v 0 + ( v 0 V ) V ] + VTa ( e z x V ) = -V p + A V + 9 e z ,
|
d t |
div V = 0, (8) d9 + Gr [ V V9 + V V T 0 + v 0 V9 ] = ^ A9 , z = - 1: V = 0, 9 = 0, d u d v (9) z = 1: — = — = w = 0, 9 = 0. d z d z |
Согласно результатам линейной теории [22], кризис стационарного режима (6) связан с развитием в областях с неустойчивой температурной стратификацией пространственных винтовых и спиральных возмущений. В настоящей статье в нелинейной постановке изучается поведение возмущений такого типа с конечной амплитудой при слабом вращении (0 < Ta < 100) за порогом устойчивости.
-
3. Винтовые возмущения
Поведение возмущений конечной амплитуды в надкритической области (при числах Грасгофа выше критического) исследуем на основе нелинейной системы безразмерных уравнений (8), (9). Уравнения винтовых возмущений выведем в предположении, что все функции не зависят от переменной y и, соответственно, у всех функций производная по у равняется нулю. При отсутствии вращения (Ta = 0) эти возмущения вырождаются в плоские [9]. Введем функцию тока возмущений дш дш и =--, w = —
дz дx и вихря возмущения скорости ди д w . Г д2ш д2ш
---= —Аш = -1 —2- + — v
дz дx I дx2 дz2
С учетом этих обозначений для пространственных винтовых, периодических по x возмущений уравнения и граничные условия принимают вид:
дф
дф , х дф дш дф дш дф дш х — + Gr и 0 ( z )— '.'. —L u "( z ) д t 2 д x д z д x д x д z д x
д t
Гд v ) д 2 ф д 2 ф дО
— Ta I I = + ,
I дz J дx2 дz2 дx
Аф + ф = 0, dv
— + Gr д t
до
— + Gr
д t
, х д v дш д v дш , , х дш д v и 0 ( z )----— + — v ‘( z ) + ——
2 д x д z д x д x д x д z
дш ( ) д0 дш дО дш дО д z 0 д x д z д x д x д z
— Via
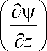
д2 v д2 v дx2 дz2,
_ Ra , / х дш
+ Gr Ж v ; ( г )&
1 Г д 2 О д 2 о)
+;
Pr ^д x 2 д z 2 J
дш
О = 0,
О = 0.
z = —1: ш = — = v = 0, дz i д v л z = 1: ш = — = ф = 0, дz
Предположим, что нижняя граница твердая, верхняя свободная, на боковых границах заданы условия периодичности
ш( t ,0, z) = ш( t, L, z), ф( t ,0, z) = ф( t, L, z), v (t ,0, z) = v (t, L, z), 0( t, 0, z) = 0( t, L, z), где L — длина волны возмущений, соответствующая критическому числу Грасгофа для фиксированного числа Тейлора, ф(t, x, z)— вихрь возмущения скорости, 0(t, x, z)— возмущения температуры. Функция тока возмущений ш(t, x, z) описывает систему движущихся вихрей, расположенных вдоль оси абсцисс и охватывающих весь поток. Вторая же компонента скорости возмущений v(t, x, z) представляет собой проекцию движения конечно-амплитудных возмущений на плоскость Oyz или Oxy . В качестве начальных возмущений для неизвестных ф, ш, v и О возьмем функцию cos(2nx/L)sin2 пz, удовлетворяющую граничным условиям (11). С помощью системы уравнений (10) с граничными условиями (11) исследуем структуру вторичных течений, возникающих в горизонтальном слое при фиксированных значениях чисел Pr и Ta и значениях числа Gr выше критического.
С привлечением «двухполевого» метода [25] задача решена численно с помощью метода сеток, Использовалась явная конечно-разностная схема с центральными разностями, дающая погрешность аппроксимации порядка О(Аt + h2). Уравнение Пуассона для функции тока возмущений решалось методом последовательной верхней релаксации. При отсутствии вращения подтвердились результаты работы [9]. В частности, за порогом устойчивости у нижней границы слоя зарождаются плоские пространственные структуры. Вблизи критического числа Грасгофа максимум функции тока растет по корневому закону. При достижении числом Грасгофа второго критического значения наблюдается скачкообразное изменение функции тока. В этой точке жестко возбуждаются вихри у свободной верхней границы. По мере дальнейшего увеличения числа Грасгофа интенсивность вихрей и тепловой поток возрастают.
Основные расчеты проведены на сетке 101 x 101. Выбор размера сетки основывался на оптимальном соотношении между точностью искомых численных результатов и временем решения задачи. Результаты получены при фиксированном значении числа Прандтля Pr = 6,7 (вода), критических числах Грасгофа Gr , = 63,32; 74,55;144,56;189,04 и соответствующих волновых числах kx = 3,25; 3,5; 3,5; 3,5 для чисел Тейлора Ta = 1; 10; 50; 100 [6]. Для каждого числа Тейлора число Грасгофа выбиралось выше критического приблизительно с надкритичностью, равной 1; 1,25; 1,5; 1,75; 2.
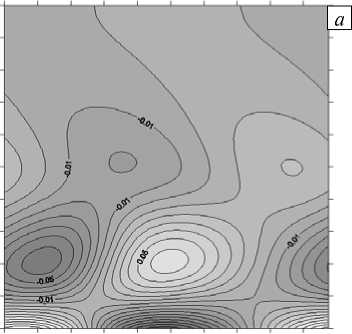
Далее представлены наиболее характерные результаты, полученные при Ta = 1;100. На рисунке 2 видно, что в надкритической области под воздействием температурной неоднородности зарождаются винтовые пространственные структуры (вихри), расположенные поперек слоя у нижней твердой границы.
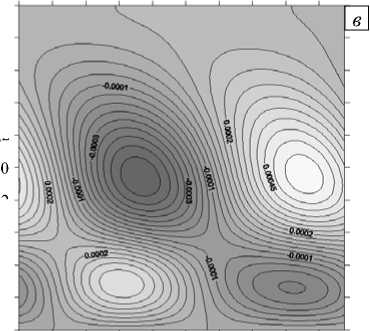
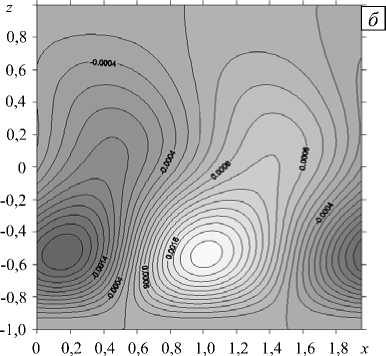
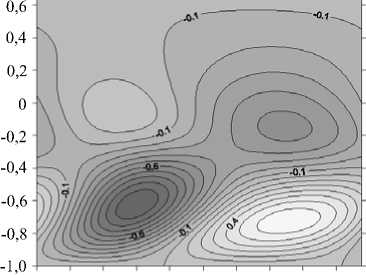
При всех рассматриваемых значениях числа Грасгофа вихрь возмущения скорости представляет собой систему винтообразных вихрей (Рис. 2 а ). Вблизи минимумов нейтральных кривых функция тока возмущений выглядят как последовательность движущихся вдоль оси абсцисс вихрей, локализованных вблизи нижней границы и охватывающих весь поток (Рис. 2 б ), а возмущение температуры — как чередующиеся теплые и холодные пятна, также расположенные вдоль оси x (Рис. 2 г ). Проекция движения, описанная функцией скорости возмущений, выглядит как система чередующихся, движущихся в одинаковом направлении пар вращающихся вихрей. Одновременно вторая компонента скорости возмущения (ориентированная поперек слоя) меняет свое значение с положительного на отрицательное (Рис. 2 в ) и таким образом изображает в плоскости O yz вращение то по часовой стрелке, то против часовой стрелки чередующихся и движущихся вихрей. В местах, где находятся холодные пятна, вихри скорости вращаются против часовой стрелки, в области теплых пятен — по часовой стрелке.
С ростом числа Грасгофа (70 < Gr < 80) начинает меняться структура температурных возмущений, прибывают вертикальные размеры тепловых пятен, их число растет. Холодные пятна сосредоточиваются в верхнем, а теплые — в нижнем слое жидкости. Вихри функции тока возмущений увеличиваются в размерах и по амплитуде.
-1,0
0,8
0.6
0.4
0,2
-0.2
-0,4
-0,6
-0,8
-1,0
а
0 0,2 0,4 0,6 0,8 1,0 1,2 1,4 1,6 1,8 х
0.6 -
0,2-
0,8
0,4
-0,2
-0,4
-0,6-
-0,8-
0 0,2 0,4 0,6 0,8 1,0 1,2 1,4 1,6 1,8 .v
0,8

0 0,2 0,4 0,6 0,8 1,0 1,2 1,4 1,6 1,8 .v
Рис. 2. Изолинии функций возмущений для Ta = 1,Gr = 70 и kx = 3,25 : вихрь ф ( а ), функция тока ф ( б ), скорость v ( в ) и температура 0 ( г )
При еще больших числах Грасгофа (80 < Gr < 120) тепловые пятна перестраиваются, укрупняются; теплые пятна группируются у нижней границы слоя, а холодные — в центре слоя. Движение вихрей становится более сложным. Вихри, вращающиеся в плоскости O xz против часовой стрелки, увеличиваются в размерах, меняется их структура, растут количество и амплитуда вихрей. Амплитуда и размеры вихрей, вращающихся по часовой стрелке, уменьшаются.
С учетом в постановке задачи физической нелинейности получены зависимости амплитуд функции тока возмущений ^ max, компоненты возмущения скорости v max, возмущения температуры 9 max и возмущения скорости Vmax = max V u 2 + v 2 + w 2 от числа Грасгофа вблизи порога устойчивости (Рис. 3).
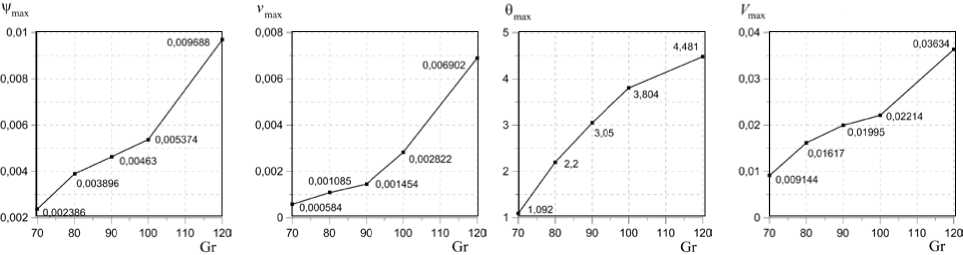
Рис. 3. Зависимости амплитуды функций возмущений от числа Грасгофа для Ta = 1
Введем понятие временного периода функций — периода повторения картины конечно-амплитудных возмущений. Временной период сокращается с ростом числа Грасгофа. Кривая зависимости периода от числа Грасгофа подчиняется гиперболическому закону. Для винтовых возмущений при фиксированном числе Тейлора (Ta = 1) и волновом числе k x = 3,25 период составляет: т per = 65/Gr1’262 .
Поведение возмущений конечной амплитуды с ростом скорости вращения до Ta = 50 при k x = 3,5 поначалу не изменяется. Размеры вихрей уменьшаются, а амплитуда вихрей увеличивается. Но с ростом скорости вращения (при Ta < 50) вихри на свободной границе появляются при меньшей надкритичности числа Грасгофа, чем при значениях Ta = 10 и Ta = 1. Временной период становится равным т per = 249/Gr1,336 . Полученные зависимости амплитуды отражены на рисунке 4.
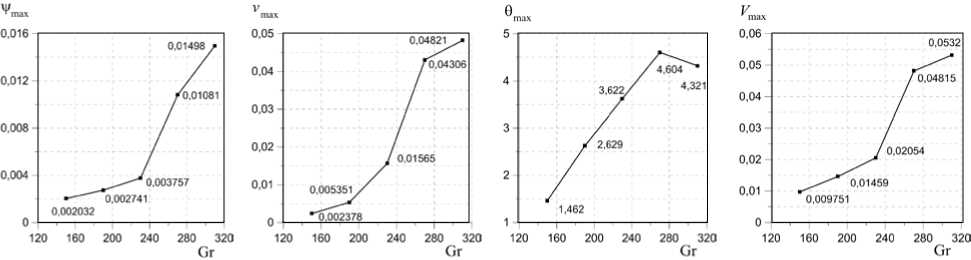
Рис. 4. Зависимости амплитуды функций возмущений от числа Грасгофа для Ta = 50
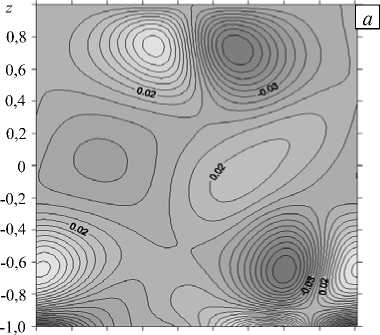
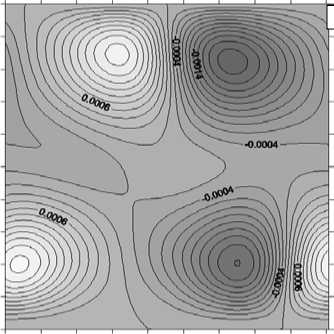
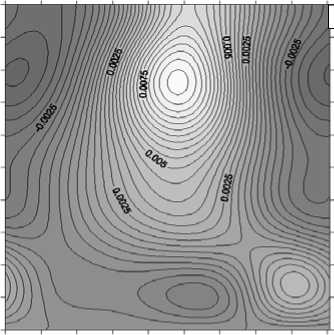
С ростом скорости вращения до Ta = 100 вблизи свободной верхней границы появляются винтообразные вихри (Рис. 5 а ). Движение становится более сложным (Рис. 5 в ). При бόльших значениях числа Грасгофа (220 < Gr < 280) меняется структура течения, возрастают вертикальные размеры тепловых пятен. Холодные пятна начинают локализоваться в нижнем, а теплые — в верхнем слое жидкости. Причем вихри, вращающиеся в плоскости O xz по часовой стрелке, укрупняются. Амплитуда вихрей, вращающихся против часовой стрелки, увеличивается.
При дальнейшем росте числа Грасгофа (280 < Gr < 400) тепловые пятна перестраиваются, их размер становится больше, теплые пятна сосредоточиваются у верхней границы слоя, а холодные — в центре слоя. Вихри, вращающиеся в плоскости O xz против часовой стрелки, увеличиваются в размерах, меняется их структура, количество сокращается; вихри возле свободной верхней границы вытесняют вихри, расположенные вдоль твердой нижней границы, амплитуда вихрей возрастает. Амплитуда и размеры вихрей, вращающихся по часовой стрелке, уменьшаются. Временной период составляет т per = 497/Gr1’373 . Полученные зависимости амплитуды представлены на рисунке 6.
О 0,2 0,4 0,6 0,8 1,0 1,2 1,4 1,6 1,8 х
О 0,2 0,4 0,6 0,8 1,0 1,2 1,4 1,6 1,8 х
О 0,2 0,4 0,6 0,8 1,0 1,2 1,4 1,6 1,8 х
Рис. 5. Изолинии функций возмущений для Ta = 100 , Gr = 280
0,8
0,6 -
0.4 -
0,2
О -
-0,2
-0,4
-0,6
-0.8
-1,0 -
-од
г
О 0,2 0,4 0,6 0,8 1,0 1,2 1,4 1,6 1,8 х
и k x = 3,5 : вихрь ф ( а ), функция тока ф ( б ), скорость v ( в )
и температура 0 ( г )
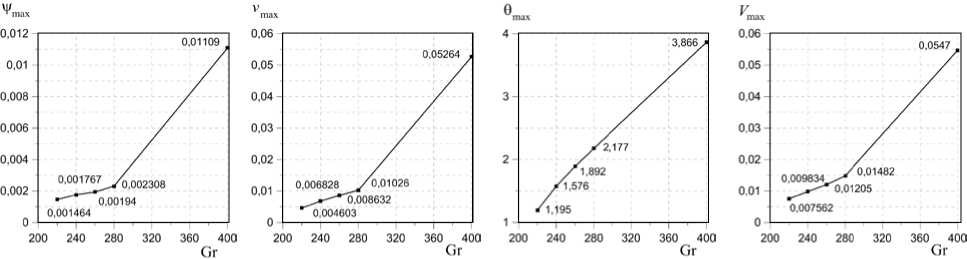
Рис. 6. Зависимости амплитуды функций возмущений от числа Грасгофа для Ta = 100
-
4. Спиральные возмущения
Уравнения спиральных возмущений выведем в предположении, что все функции не зависят от переменной x и, соответственно, производная по x у всех функций равняется нулю. Введем функцию тока возмущений dvdv v =--, w =, dz и вихря возмущения скорости dv dw Ф = - dz dy
-A¥ =
f d 2¥d
I 2" +2r I.( dy2 dz2 )
Для пространственных спиральных, периодических по y возмущений уравнения имеют следующий вид:
дФ Г , хдФ дТдФ дТдФ дТ „, J /т^Гд и ) д 2 Ф д 2 Ф 50
+ Gr v0(z)++v0(z) + VTa| I = 2- + 2, д t L дy дz дy дy дz дy J ( дz J дy2 дz2 дy
АТ + Ф = 0, д U _ / x д и
— + Gr v 0 ( z )— д t с"
ди дТ ди дТ ----+--и о (z) + дy дz дy дy
дТд и 1 .'дТ1'' д 2 и д 2 и --+ VTa I I = — 2 + — 2 , д y д z J ( д z J д y 2 д z 2
д0
д0 , x д0 дТ д0 дТ д0 + Gr v 0 (z)+ д t L ^y дz дy дy дz
д t
_ Ra , , хдТ
+ и + Gr —j=v ‘ ( z )---
J L vra0 y j
1 Г д 2 0 д 2 0)
I + I ,
Pr (д y 2 д z 2 J
а соответствующие граничные условия выглядят как z = -1: T=---= и = 0, 0 = 0,
.д z (13)
z = 1: Т= — = Ф = 0, 0 = 0;
дz нижняя граница — твердая, верхняя — свободная, на боковых границах выполняются условия периодичности
Т( t ,0, z) = Т( t, L, z), Ф( t ,0, z) = Ф( t, L, z), и (t ,0, z) = и (t, L, z), 0( t ,0, z) = 0( t, L, z), где L — длина волны возмущений, отвечающая критическому числу Грасгофа при фиксированном числе Тейлора, Ф(t,y, z) — вихрь возмущения скорости, 0(t, y,z) — возмущения температуры. Функция тока возмущений Т(t, y, z) описывает систему движущихся вихрей, расположенных вдоль оси y и охватывающих весь поток. Первая же компонента скорости возмущений u(t, y, z) изображает проекцию движения конечно-амплитудных возмущений на плоскость Oxz или Oxy . Начальные возмущения неизвестных Ф, Т, и и 0 бралась в виде функции cos(2nx/L)sin2 пz, удовлетворяющей граничным условиям (13).
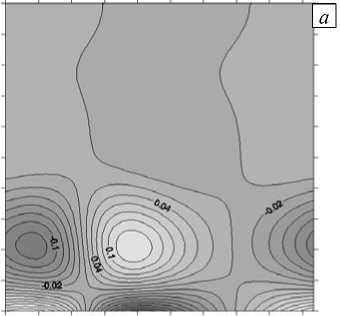
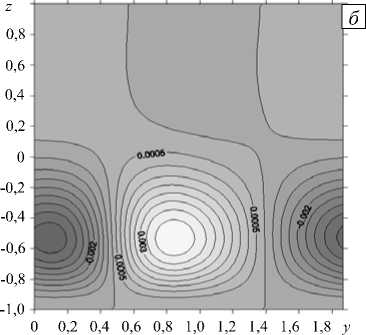
С помощью системы уравнений (12) с граничными условиями (13) исследовалась структура вторичных течений, возникающих в горизонтальном слое при фиксированных значениях чисел Pr и Ta для значений Gr выше критического. Использовались критические числа Грасгофа Gr, = 57,04; 129,69; 179,31 и соответствующие волновые числа k y = 3,4; 3,5; 3,5 для чисел Тейлора Ta = 1; 42; 70 [22]. Далее представлены наиболее характерные результаты, полученные при Ta = 1; 70 (Рис. 7). Задача решалась аналогично случаю винтовых возмущений.
а
0 0.2 0,4 0,6 0.8 1,0 1,2 1,4 1,6 1,8 v
0.8
0,6
0.4
0,2
-0.2
-0,4
-0.6
-0,8
-1,0
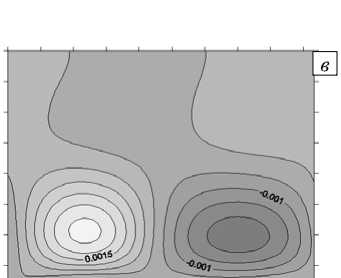
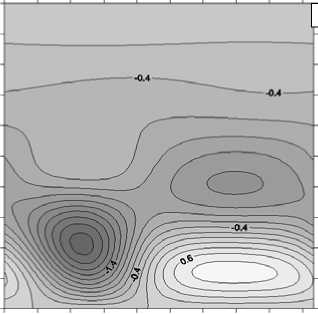
Рис. 7. Изолинии функций возмущений для Ta = 1, Gr = 70 и k y = 3,4 вихрь Ф ( а ), функция тока Т ( б ), скорость и ( в ) и температура 0 ( г )
в о oois
0.8
0,6
0.4
0,2
-0.2
-0.4
-0.6
-0.8
-1,0

0 0,2 0,4 0.6 0,8 1.0 1.2 1,4 1,6 1,8 у
О 0,2 0.4 0,6 0,8 1,0 1.2 1,4 1,6 1.8 у
Рис. 7. Продолжение
С ростом числа Грасгофа (70 < Gr < 100) меняется структура течения, увеличиваются вертикальные размеры тепловых пятен, число их становится больше. Холодные пятна начинают локализоваться в верхнем, а теплые — в нижнем слое жидкости. В случае спиральных возмущений первая компонента скорости возмущения меняет свое значение с положительного на отрицательное и направлена поперек слоя (Рис. 7 в ) и таким образом описывает в плоскости O xz вращение то по часовой стрелке, то против часовой стрелки чередующихся движущихся вихрей.
При дальнейшем росте числа Грасгофа (Gr > 120) тепловые пятна перестраиваются, расширяются, теплые пятна локализуются у нижней границы слоя, а холодные — в центре слоя. Вихри также увеличиваются в размерах, количество и амплитуда вихрей растут. Начинают появляться вихри на свободной верхней границе. Временной период составляет т per = 249/Gr1,189. Полученные вблизи порога устойчивости зависимости от числа Грасгофа амплитуд функции тока возмущений ¥ max, компоненты возмущений скорости u max и температуры отражены на рисунке 8.
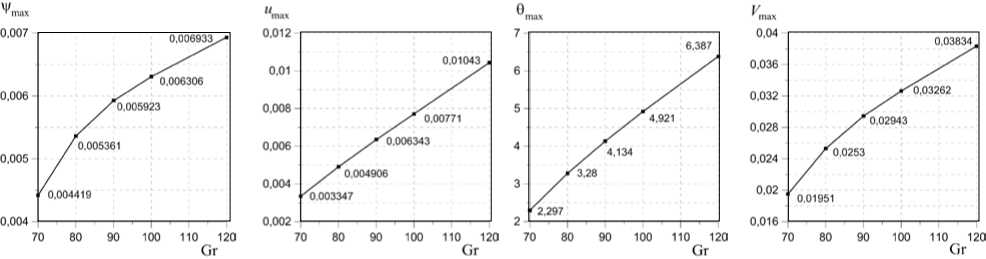
Рис. 8. Зависимости амплитуды функций возмущений от числа Грасгофа для Ta = 1
В рамках линейной теории при Ta < 42 наблюдается только одна область неустойчивости, которая располагается выше любой нейтральной кривой. При значениях Ta > 42 появляется вторая зона неустойчивости, которая с ростом числа Тейлора расширяется.
Поведение возмущений скорости вращения при значениях числа Тейлора, меньших или равных 42, и k y = 3,5 меняется незначительно. Возмущения образуют систему винтообразных вихрей. С ростом числа Грасгофа тепловые пятна перестраиваются, их размер увеличивается, теплые пятна локализуются у верхней и нижней границ слоя, а холодные — в центре слоя. При этом амплитуда и размеры холодных пятен превышают амплитуду теплых в два раза. Амплитуда вихрей возрастает, размеры уменьшаются. Появляются вихри на свободной верхней границе. Временной период равняется т per = 48/Gr1,022 . Полученные зависимости амплитуды представлены на рисунке 9.
Для Ta = 70 при небольшом росте числа Грасгофа (180 < Gr < 200) меняется структура тепловых пятен, становятся больше их вертикальные размеры. Холодные пятна начинают локализоваться в центре,
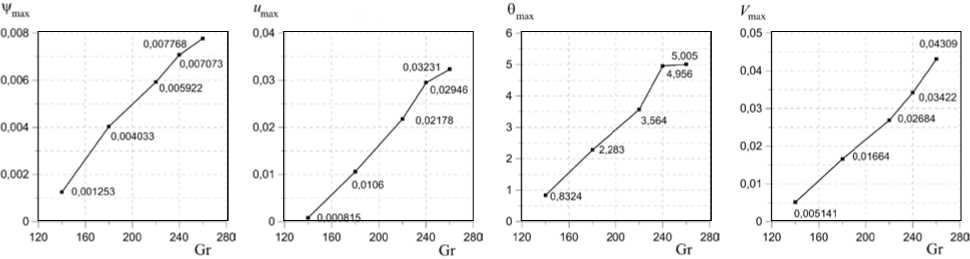
Рис. 9. Зависимости амплитуды функций возмущений от числа Грасгофа для Ta = 42
а теплые — в верхнем слое жидкости. Амплитуда вихрей увеличивается. Размеры вихрей падают. Вихри концентрируются около свободной верхней границы. На нижней границе вихри отсутствуют.
При дальнейшем росте числа Грасгофа (220 < Gr < 260) тепловые пятна перестраиваются, становятся более крупными; теплые пятна собираются у верхней и нижней границ слоя, а холодные — в центре слоя. Амплитуда и размеры холодных пятен значительно превышают аналогичные характеристики теплых пятен. Амплитуда вихрей увеличивается. Размеры вихрей уменьшаются. Появляются вихри на твердой нижней границе (Рис. 10).
0,8
0,6
0,4
0,2
О
-0,2
-0,4
-0,6
-0,8
-1,0
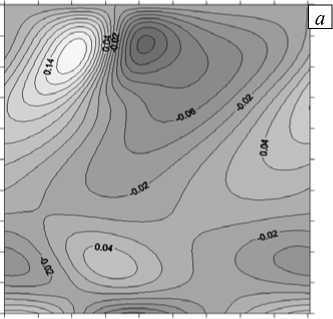
а охм
0 0,2 0,4 0,6 0.8 1,0 1,2 1,4 1.6 1,8 у
-0.8 ;
б
0 0,2 0.4 0.6 0,8 1,0 1.2 1.4 1,6 1,8 у
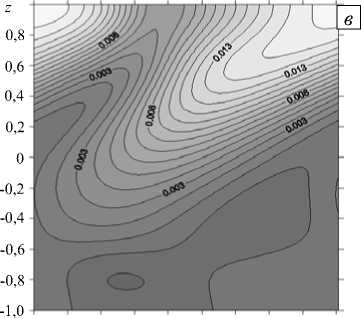
0 0,2 0,4 0,6 0,8 1,0 1,2 1,4 1,6 1,8 у
0,8
0,6
0,4 -
0,2 ■
-0,2 -
-0.4
-0,6 -
-0,8
-1.0
г
0 0,2 0,4 0.6 0,8 1,0 1,2 1,4 1,6 1,8 у
Рис. 10. Изолинии функций возмущений для Ta = 70 , Gr = 260 и k y = 3,5 : вихрь Ф ( а ), функция тока Т ( б ), скорость и ( в ) и температура 0 ( г )
После Gr = 260 резко увеличиваются амплитуда и размеры холодных пятен. Движение становится менее упорядоченным. Размеры же вихрей, наоборот значительно падают. После Gr = 310 размеры вихрей и теплых пятен начинают расти. Амплитуда и размеры холодных пятен уменьшаются.
Найденные зависимости амплитуды и временного периода функций т per от числа Грасгофа отражены, соответственно, на рисунках 11 и 12.
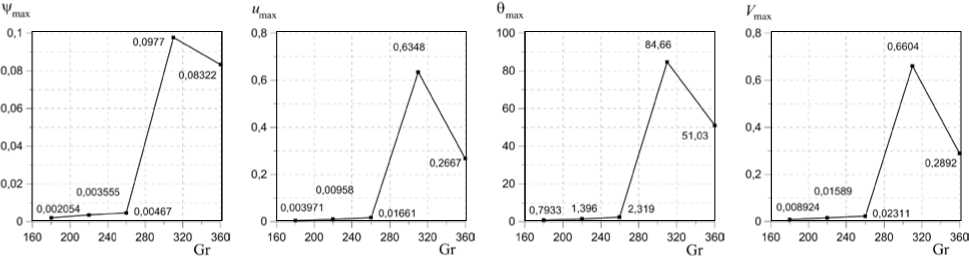
Рис. 11. Зависимости амплитуды функций возмущений от числа Грасгофа для Ta = 70
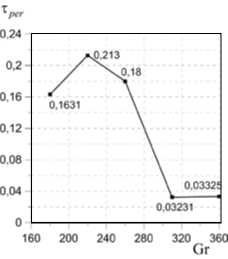
Рис. 12. Зависимость временного периода функций от числа
Грасгофа для Ta = 70
-
5. Заключение
Поведение возмущений конечной амплитуды, возникающих в слое жидкости при значениях числа Грасгофа выше критического, исследовано в нелинейной постановке. Образующаяся нелинейная система дифференциальных уравнений разрешена с привлечением метода сеток. Результаты численного решения задачи позволили сделать оценку поведения возмущений, получить скоростные характеристики, амплитуду и период их повторений.
Выяснено, что вращение приводит к возникновению надкритичных возмущений в виде нестационарных винтообразных вихрей, расположенных в потенциально неустойчивых температурных зонах, движущихся периодически вдоль границ слоя. Возмущения температуры представляют собой систему чередующихся теплых и холодных пятен, ориентированных на границах слоя в направлении изменения градиента температуры.
С ростом числа Тейлора вихри, первоначально сосредоточенные возле свободной верхней границы, вытесняют вихри, расположенные вдоль твердой нижней границы; амплитуда вихрей увеличивается.
С ростом числа Грасгофа тепловые пятна перестраиваются, укрупняются, теплые пятна локализуются у верхней и нижней границ слоя, а холодные — в центре слоя. Движение становится более сложным. Сокращается временной период повторения картины конечно-амплитудных возмущений.
Работа выполнена при финансовой поддержке РФФИ (проект № 13-01-96001-р_урал_а).
Список литературы Конечно-амплитудные возмущения адвективных течений в горизонтальном слое несжимаемой жидкости со свободной верхней границей при слабом вращении
- Аристов С.Н., Зимин В.Д. Адвективные волны во вращающемся шаровом слое: Препринт № 145/ИМСС, Уральский научный центр, АН СССР. -Свердловск, 1986. -50 с.
- Аристов С.Н., Фрик П.Г. Динамика крупномасштабных течений в тонких слоях жидкости: Препринт № 146/ИМСС, Уральский научный центр, АН СССР. -Свердловск, 1987. -48 с.
- Аристов С.Н., Фрик П.Г. Крупномасштабная турбулентность в тонком слое неизотермической вращающейся жидкости//МЖГ. -1988. -№ 4. -С. 48-55.
- Педлоски Дж. Геофизическая гидродинамика. В 2-х томах. -М.: Мир, 1984. -Т. 1. -398 с.
- Ekman V.W. On the influence of the Earth’s rotation on ocean currents//Arkiv Mater., Astron., Phys. -1905. -Vol. 2, no. 11. -P. 1-52 p.
- Аристов С.Н., Шварц К.Г. Вихревые течения адвективной природы во вращающемся слое жидкости. -Пермь: Изд-во ПГУ, 2006. -154 с.
- Остроумов Г.А. Свободная конвекция в условиях внутренней задачи. -М.: Гостехтеориздат, 1952. -286 с.
- Мызников В.М. Конечно-амплитудные конвективные движения жидкости в горизонтальном слое с продольным градиентом температуры//Математические модели течений жидкости: Тр. 6-го Всесоюз. семинара по числ. методам механики вязкой жидкости. -Новосибирск: ИТПМ СО АН СССР, 1978. -С. 176-186.
- Мызников В.М. Конечно-амплитудные пространственные возмущения адвективного движения в горизонтальном слое со свободной границей//Конвективные течения. -Пермь: Изд-во ПГПИ, 1981. -С. 83-88.
- Gershuni G.Z., Laure P., Myznikov V.M., Roux B., Zhukhovitsky E.M. On the stability of plane-parallel advective flows in long horizontal layers//Microgravity Q. -1992. -Vol. 2, no. 3. -P. 141-151.
- Аристов С.Н., Шварц К.Г. Об устойчивости адвективного течения во вращающемся горизонтальном слое жидкости//МЖГ. -1999. -№ 4. -С. 3-11.
- Шварц К.Г. Конечно-амплитудные пространственные возмущения адвективного течения во вращающемся горизонтальном слое жидкости//Вычислительные технологии. -2001. -Т. 6, Ч. 2, Спец. выпуск. -Труды Международной конференции RDAMM-2001. -С. 702-707. (URL: http://www.ict.nsc.ru/ws/NikNik/1459/rep1459.pdf).
- Тарунин Е.Л., Шварц К.Г. Исследование линейной устойчивости адвективного течения методом сеток//ЖВТ. -2001. -Т. 6, № 6. -С. 108-117.
- Schwarz K.G. Instability of advective flow in rotating horizontal layer of liquid//Selected Papers of the International conference “Fluxes and Structures in Fluids”. St. Petersburg, Russia, June 23-26, 2003. -Moscow: IPM RAS, 2004. -P. 164-171.
- Гершуни Г.З., Жуховицкий Е.М., Непомнящий А.А. Устойчивость конвективных течений. -М.: Наука, 1989. -320 с.
- Шварц К.Г. Исследование устойчивости адвективных течений во вращающемся слое жидкости//Вестник Пермского университета. Математика. Механика. Информатика. -2013. -№ 1(13). -С. 54-61.
- Imaishi N., Shi W. Thermocapillary convection in a shallow annular pool of silicone oil//Engineering Sciences Report, Kyushu University. -2006. -Vol. 28, no. 1. -P. 1-8.
- Евграфова А.В., Сухановский А.Н. Численное моделирование крупномасштабного течения в цилиндрическом слое жидкости с локальным подогревом снизу//Вестник Пермского университета. Математика. Механика. Информатика. -2011. -№ 5(9). -С. 79-82.
- Любимова Т.П., Никитин Д.А. Устойчивость адвективного течения в горизонтальном канале прямоугольного сечения с адиабатическими границами//МЖГ. -2011. -№ 2. -С. 82-91.
- Любимова Т.П., Никитин Д.А. Трехмерные адвективные течения в горизонтальном цилиндре квадратного сечения с теплоизолированными боковыми границами//Вычисл. мех. сплош. сред. -2011. -Т. 4, № 2. -С. 72-81.
- Yu J.-J., Ruan D.-F., Li Y.-R., Chen J.-C. Experimental study on thermocapillary convection of binary mixture in a shallow annular pool with radial temperature gradient//Exp. Therm. Fluid Sci. -2015. -Vol. 61. -P. 79-86.
- Shvarts K.G., Boudlal A. Effect of rotation on stability of advective flow in horizontal liquid layer with a free upper boundary//J. Phys.: Conf. Ser. -2010. -Vol. 216, no. 1. -012005.
- Никитин Н.В., Никитин С.А., Полежаев В.И. Конвективные неустойчивости в гидродинамической модели роста кристаллов методом Чохральского//Успехи механики. -2003. -Т. 2, № 4. -С. 63-105.
- Гершуни Г.З., Жуховицкий Е.М. Конвективная устойчивость несжимаемой жидкости. -М.: Наука, 1972. -392 с.
- Тарунин Е.Л. Вычислительный эксперимент в задачах свободной конвекции. -Иркутск: Изд-во Иркут. ун-та, 1990. -228 с.


