Конечно-элементная оценка влияния открытой проникающей черепно-мозговой травмы на посмертное температурное поле головы

INFORMATION TECHNOLOGY IN MEDICINE                                        УДК 340.624.4.6-053.31

Одним из наиболее востребованных методов термометрического определения давности наступления смерти (ДНС) по-прежнему остается метод К. Хенссге, основанный на измерении краниоэнцефальной температуры [1]. Математическим выражением данного метода является феноменологическая модель

T - T a = 1 , 135 e~⁰¹¹²⁷t - 0 , 135 e ^4,07 t ,     (1)

,, 0a где Т – краниоэнцефальная температура трупа, °С; Та – температура внешней среды, °С; Т0 – начальная краниоэнцефальная температура в момент наступления смерти человека, °С; t – ДНС, ч [1, 2].

Как показывает выражение (1), для его использования на практике помимо измерения краниоэнцефальной температуры трупа и температуры внешней среды необходимо также оценить начальную температуру глубинных отделов головного мозга в момент наступления смерти, значение которой, согласно рекомендациям К. Хенссге, следует принимать равным 37,2 °С [1]. Поэтому любые условия охлаждения, вызывающие отклонения начальной краниоэнцефальной температуры от ее заданного в модели (1) значения, являются противопоказанием к практическому использованию последней. В числе подобных условий, способных вызывать как локальное, так и системное повышение температуры, рассматривается широкий спектр вне- и внутричерепных повреждений (церебральные ушибы, внутричерепные кровоизлияния) [3, 4]. Одним из таких повреждений, степень влияния которого на посмертный теплообмен анатомических структур головы еще не выяснено, является открытая проникающая черепно-мозговая травма (ОПЧМТ). В настоящее время указанная научно-практическая задача может быть решена с помощью ко- нечно-элементного анализа, ставшего доступным благодаря широкому распространению компьютерных технологий.

В связи с изложенным, целью исследования явились разработка конечно-элементной модели (КЭМ) посмертного теплообмена головы при наличии ОПЧМТ и оценка степени ее влияния на посмертное температурное поле данной области тела.

Материал и методы исследования

Методологический дизайн исследования представляет собой конечно-элементное моделирование посмертного температурного поля головы, выполненное с использованием приложения ELCUT 6.5.

Геометрию мозгового отдела головы представляли в виде многослойной полусферы с равномерным распределением пяти однородных слоев с различными теплофизическими свойствами: кожно-апоневротического лоскута, костей свода черепа, ликвора субарахноидального пространства, поверхностных и глубинных отделов головного мозга. Выделение указанных отделов было вызвано необходимостью нахождения начального температурного поля головного мозга, в глубинных отделах являющегося однородным, а в поверхностных – характеризующегося монотонным снижением температуры. Благодаря осевой симметрии геометрия КЭМ была представлена одним квадрантом, что позволило свести задачу к классу двумерных.

Теплофизические свойства актуальных анатомических слоев задавали согласно данным литературы (табл. 1). Начальную температуру глубинных отделов мозга принимали, как и в рамках феноменологической модели К. Хенссге, равной 37,2 °С. При нахождении начального температурного поля на метках ребер КЭМ задавали значения температуры, присущие тканям головы при температуре поверхности кожи 31 °С (см. табл. 1). Итоговая двумерная геометрическая модель интактного мозга состояла из 5 блоков, представлявших собой 5 актуальных анатомических слоев головы, а также из 11 вершин и 15 соединяющих их ребер. Построенная сетка включала 230 конечных элементов треугольной формы.

Для воспроизведения ОПЧМТ в исходной геометрической модели в кожно-мышечном лоскуте головы, черепе, оболочках и ткани головного мозга был создан клиновидный дефект глубиной 33 мм, занимающий 2,2 % поверхности головы (рис. 1).

В проекции субарахноидального пространства также создали отдельный блок, моделирующий оболочечные кровоизлияния суммарной толщиной 2 мм и площадью 22,2 % конвекситальной поверхности полушария большого мозга. В свойствах этого блока задавали теплофизические параметры крови.

Таблица 1. Теплофизические свойства тканей головы [5, 6]

Table 1. Thermophysical properties of head tissues [5, 6]

Параметр	Скальп	Череп	Ликвор	Мозг		Кровь
Температура поверхности, °С	31	34	35	35,5	37,2	37,0
Теплопроводность, Вт/(м·К)	0,34	1,16	0,618	0,503		0,54
Теплоемкость, Дж/(кг ⋅ К)	4000	2300	4174	3700		3800
Плотность, кг/м3	1000	1500	1003	1050		1050
Толщина, мм	5	5	2	17	69	2/15

Примечание. Для ликвора приведены значения теплопроводности и теплоемкости воды при температуре 30 °С. Для мозга указаны показатели его поверхностных и глубинных отделов.

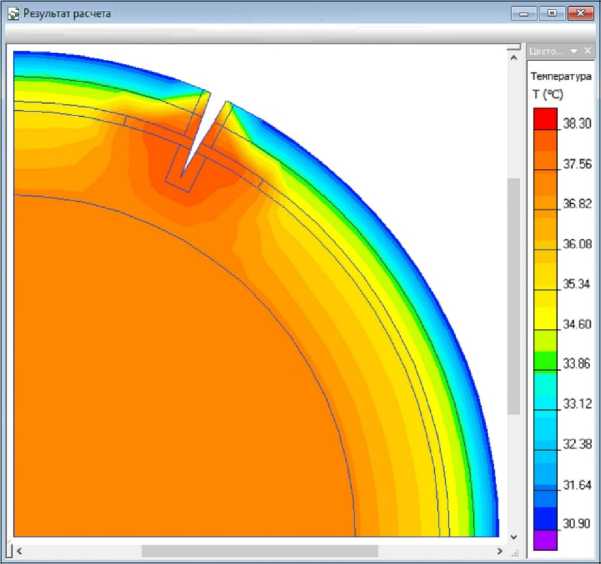
Рисунок 1. Начальное температурное поле головы при наличии ОПЧМТ

Figure 1. The initial temperature field of the head in the presence of an open penetrating traumatic brain injury

Зону клиновидного дефекта в КЭМ ограничивали серией ребер для моделирования перифокальной зоны размозжения и ушиба тканей с повышенной за счет гиперемии температурой. Перифокальная зона также включала блок оболочечных кровоизлияний. На всех ребрах этой зоны, кроме расположенных внутри нее и на внешнем ребре модели, задавали более высокую начальную температуру, равную 38,2 °С.

Построенная сетка конечных элементов КЭМ с наличием ОПЧМТ состояла из 247 узлов, а геометрическая модель включала 17 блоков, 50 ребер и 34 вершины. Заданная геометрия и названные граничные условия позволили смоделировать начальное температурное поле головы, отличающееся повышением температуры в области стенок проникающей раны, ее перифокальных отделов, зоны ассоциированных оболочечных кровоизлияний, а также ушиба мозга (см. рис. 1).

После геометрической и физической идеализации задачи в случае интактного головного мозга и при наличии ОПЧМТ находили прижизненное температурное поле головы, которое затем задавали в качестве начального условия посмертного теплообмена. При последующем нахождении посмертного температурного поля актуальный расчетный период принимали равным 24 ч с шагом интегрирования в 600 с. На внешнем ребре КЭМ задавали конвективный теплообмен с воздушной средой, протекающий при постоянной внешней температуре по закону Ньютона – Рихмана, с различными коэффициентами теплоотдачи. На всех этапах решения задачи задавали отсутствие в КЭМ внутренних и внешних источников тепловыделения.

Отладку КЭМ интактного мозга осуществляли путем оценки сходимости кривых охлаждения, полученных с помощью КЭМ, и известных математических моделей охлаждения глубоких и поверхностных тканей трупа с общепризнанной валидностью для температуры внешней среды 10 °С. В качестве последних использовали уравнение (1) К. Хенс-сге и модель охлаждения поверхности тела в соответствии с законом Ньютона – Рихмана [2]. Отладка КЭМ теплообмена интактного мозга показала ее максимальную точность в стандартных условиях охлаждения головы при задании на внешнем ребре конвективного теплообмена с коэффициентом теплоотдачи, равным 6 Вт/(м2·К). Под стандартными условиями понималось охлаждение данной области мертвого тела в одной воздушной среде при отсутствии принудительной конвекции и контакта с другими физическими телами.

Найденные путем отладки КЭМ интактного мозга условия конвективного теплообмена затем задавали в КЭМ с наличием ОП-ЧМТ. Во всех моделях под краниоэнцефаль-ной понимали температуру в точке начала координат (радиальная и угловая полярные координаты равны нулю). Визуализацию термограмм выполняли с помощью приложения Statistica (StatSoft) 7.0.

Результаты исследования и их обсуждение

Анализ картины посмертного температурного поля показал, что даже при наличии проникающей раны головы уже через 2 ч после наступления смерти неоднородность поля вдоль его угловой координаты практически исчезает. Начиная с этого момента градиент температур в расчетной области сохраняется лишь в радиальном направлении. Термограммы в точках начала координат и на внешнем ребре КЭМ интактного мозга и с наличием ОПЧМТ совпадали на всем протяжении (рис. 2).

Также вдоль радиусов обеих геометрических моделей были проведены контуры интегрирования с одинаковыми координатами ко- нечных точек. В модели с наличием проникающей раны головы контур проходил через ее край и перифокальную зону. В нулевой момент времени термограммы обеих моделей совпадали до зоны раны (рис. 3).

В области проникающего ранения отмечалось выраженное повышение температуры тканей по сравнению с КЭМ интактного мозга. Однако данное различие термограмм исчезало через 2 ч после начала процесса охлаждения из-за теплообмена нагретых участков головы с соседними (см. рис. 3).

Таким образом, наличие ОПЧМТ не оказывает существенного влияния на посмертную динамику краниоэнцефальной температуры и температуры поверхностных тканей. Локальное повышение температуры в области проникающей раны, в перифокальных тканях и ассоциированных оболочечных кровоизлияниях исчезает через 2 ч от начала охлаждения. Поэтому краниоэнцефальная и поверхностная температура головы могут использоваться для определения ДНС при наличии ОПЧМТ. Определение ДНС при этом может быть осуществлено методом конечноэлементного моделирования посмертного теплообмена или с помощью уравнения (1) К. Хенссге.

Следует отметить, что полученные результаты конечно-элементного моделирования верны только в том случае, если ОПЧМТ не приводит к срыву церебральной терморегуляции с последующим развитием лихорадки и гипертермического варианта танатогенеза. Между тем, лихорадка нейрогенного или инфекционного генеза является частым осложнением внутричерепных оболочечных кровоизлияний, поражающим до 40 % пациентов уже в течение первых 48 часов после их развития [4]. Указанное обстоятельство следует учитывать при задании начальной краниоэн-цефальной температуры в любых математических моделях охлаждения трупа.

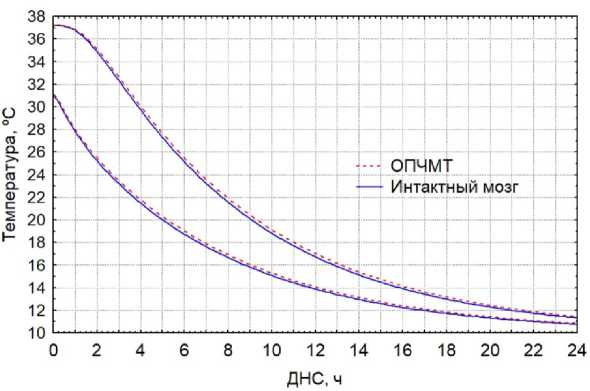
Рисунок 2. Термограммы в точках начала координат и на внешнем ребре КЭМ при наличии и отсутствии

ОПЧМТ при внешней температуре 10 °С

Figure 2. Thermograms at the center of the origin points and on the outer edge of the finite element model in the

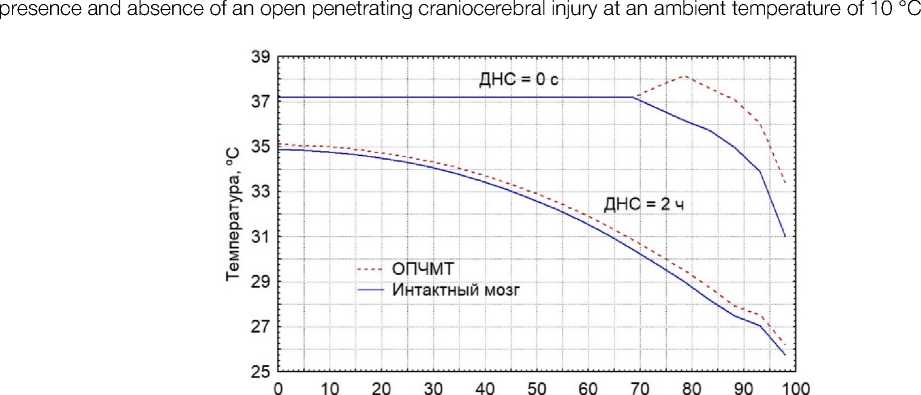
Радиальная координата, мм

Рисунок 3. Термограммы вдоль радиуса КЭМ в момент и через 2 ч после наступления смерти при наличии и отсутствии ОПЧМТ при внешней температуре 10 °С

Figure 3. Thermograms along the radius of the finite element model at the time and 2 hours after the onset of death in the presence and absence of open penetrating traumatic brain injury at an ambient temperature of 10 °C

Предложенные принципы конечноэлементного моделирования также могут быть использованы при нахождении посмертного температурного поля головы при ОПЧМТ любых размеров и геометрии. Построенная КЭМ является масштабируемой и позволяет учитывать размеры проникающей раны и объем внутричерепных оболочечных кровоизлияний, а также реальную толщину и тепло- физические параметры актуальных анатомических слоев головы, зарегистрированные в ходе судебно-медицинского исследования трупа. Целесообразно при нахождении посмертного температурного поля рассматривать также значения начальной краниоэнце-фальной температуры, учитывающие возможность гипертермического варианта танатоге-неза.

Заключение

• 1.    Разработана двумерная КЭМ нахождения посмертного температурного поля головы при ОПЧМТ в условиях конвективного теплообмена с воздушной средой, учитывающая теплофизические параметры анатомических слоев данной области тела.

• 2.    С помощью конечно-элементного анализа доказано отсутствие значимого локального влияния открытой проникающей раны

• 3.    Краниоэнцефальная температура может использоваться для определения ДНС при наличии ОПЧМТ. При задании начальной краниоэнцефальной температуры в любых математических моделях охлаждения трупа целесообразно учитывать возможность гипертермического варианта танатогенеза.

головы на посмертную динамику краниоэнце-фальной и поверхностной температуры.