Конечно-элементное моделирование пористых термоупругих композитов с учетом микроструктуры

В последнее время наблюдается повышенный интерес к композитным материалам сложной структуры, которые обнаруживают весьма эффективные свойства, важные для многих практических применений. Остаются актуальными и проблемы определения эффективных свойств традиционных композитов со связанностью физико-механических полей, например, свойств пороупругих или термоупругих пористых тел с учетом взаимосвязи их микроструктуры и анизотропии.

Объяснить и промоделировать некоторые важные характеристики, а также дать рекомендации по эффективности различных соотношений и связностей структур составляющих фаз позволяют математические и компьютерные исследования композитных материалов. Благодаря им задачи вычисления эффективных модулей для термоупругих композитных сред изучены в настоящее время достаточно подробно. Данные вопросы отражены как в ставших уже классическими монографиях (например [1, 2]), так и во многих других публикациях. Тем не менее различные аспекты моделирования термоупругих композитов обсуждаются и в работах последних лет. В этой связи можно отметить статьи [3–8], в которых рассматриваются пористые термоупругие материалы.

В настоящей работе развивается подход, основанный на методах эффективных модулей механики композитов, компьютерном моделировании представительных объемов с учетом их микроструктуры и на применении конечно-элементных технологий решения связанных задач термоупругости для анизотропных пористых тел. Основные идеи предлагаемого похода демонстрируются на примере пористого кремния при различных предположениях о его микроструктуре. В результате вычислительных экспериментов показано, что эффективные термоупругие модули могут существенно зависеть от структуры представительного объема композитного материала.

2.    Методика моделирования свойств термоупругих композитов

Пусть Q — представительный объем композитного тела, Г = 5Q — его граница, n — вектор внешней единичной нормали к Г , x = { x 1 , x ₂ , x ₃} — радиус-вектор точки в декартовой системе координат. Рассмотрим в объеме Q неоднородный анизотропный термоупругий материал. Тогда в рамках статической линейной теории термоупругости имеем следующую систему определяющих дифференциальных уравнений в векторно-матричной форме:

L * ( V ) ■ T = 0, T = c ■ S - е е , S = L ( V ) ■ u , V- q = 0,     q = - k ■Ve ,

d i

где L * ( V ) = 0

0   0

d ₂ 0

0    d ₃

0 d ₃

d ₃ 0

8 2 d i

8 1 0

V=U ’,

a

T = { a_n, g ₂₂, g ₃₃, g ₂₃, o ₁₃, g ₁₂ } — (псевдо-) вектор

напряжений □ ij , c — матрица упругих жесткостей размером 6 х 6, S = { 6 11 , е ₂₂ , е ₃₃ , 2 е ₂₃ , 2 е ₁₃ , 2 е ₁₂} — (псевдо-) вектор деформаций е ij , q — трехмерный вектор потока тепла, е — приращение температуры от естественного состояния, в = { Р_П , в ₂₂ , в ₃₃ , в ₂₃ , в ₁₃ , в ₁₂} — шестимерный (псевдо-) вектор коэффициентов температурных напряжений р ij , k — матрица коэффициентов теплопроводности размером 3 х 3 . Здесь в векторно-матричных обозначениях тензорных величин использован общепринятый в технической литературе закон соответствия ( ij ) о а между парами индексов ( ij ) ~ ( ji ), где i , j = 1, 2, 3, и одномерными индексными массивами а = 1, 2, 3, 4, 5, 6: (11) о 1; (22) о 2; (33) о 3;

(23)~(32) о 4; (13)~(31) о 5; (12)~(21) о 6.

Неоднородная термоупругая среда имеет модули, являющиеся функциями координат, то есть c = c ( x ), в = в ( x ), k = k ( x ), причем эти модули могут сильно изменяться в пределах представительного объема Q . Приняв соответствующие граничные условия на Г = dQ , можно найти решение задачи (1), (2) в объеме Q с неоднородными материальными свойствами. Тогда осреднение по Q полученных характеристик решения (напряжений, потоков тепла и других) и сравнение их с аналогичными величинами для однородной среды (среды сравнения) позволят определить эффективные модули композитного материала. Заметим, что в случае анизотропной среды проблема нахождения полного набора эффективных модулей требует решения нескольких задач рассматриваемого типа при различных граничных условиях, причем число таких задач зависит от предполагаемого вида кристаллографической системы среды сравнения.

Здесь основными проблемами являются задание представительного объема, формулировка граничных задач для композитной среды и среды сравнения, а также выбор технологии решения задач для неоднородных сред. Следуя разработанным ранее методам моделирования пористых пьезоэлектрических материалов [9-11], рассмотрим аналогичные подходы применительно к задачам термоупругости.

Для термоупругой однородной среды сравнения примем, что ее поведение описывается теми же уравнениями (1), (2), но с неизвестными постоянными модулями c f , в eff и k eff . Предположим, что на границе Г = dQ имеют место следующие краевые условия:

u = L * ( x ) ■ S ₀ , е = е ₀ , x еГ ,

где S ₀ = { е ₀₁₁ , е ₀₂₂ , е ₀₃₃ , 2 е ₀₂₃ , 2 е ₀₁₃ ,2 е ₀₁₂ } ; e ₀ j , е ₀ — некоторые не зависящие от x величины. Тогда u = L * ( x ) ■ S ₀ , S = S ₀ , е = е ₀ , T = T ₀ = c ^eff ■ S ₀ - в ^eff е ₀ будут давать решение задачи (1)-(3) в объеме Q однородной среды сравнения. Заметим, что при е = е ₀ уравнения (2) выполняются тождественно, если q = q ₀ = 0 , но эта чисто температурная задача здесь фактически не используется.

Решим теперь эту же задачу (1)-(3) в случае неоднородной среды. Допустим, что для нее и среды сравнения осредненные напряжения равны: (т) = (Т0); здесь и далее угловые скобки (...) означают среднюю по объему величину: (...) = (1/Q)J(...)dQ . Таким образом, для эффективных модулей композита q выполняется уравнение ceff ■ S0 - вeff е0 = (T), где S0 и е0 — заданные согласно граничным условиям (3) величины. Тогда, даже в предположении общего вида анизотропии среды сравнения, можно вычислить все модули жесткости cf и коэффициенты температурных напряжений рf.

Действительно, полагая в (3) S 0 = б ₀ h , , б ₀ = const, 9 0 = 0, где £ — некоторый фиксированный индекс ( h _z — вектор из шестимерного базиса для компонент тензора деформаций; h j = e j e j ( j = 1, 2, 3); h ₄ = ( e ₂ e ₃ + e ₃ e ₂ ) /2; h ₅ = ( e 1 e ₃ + e ₃ e 1 ) /2 ; h ₆ = ( e 1 e ₂ + e ₂ e 1 ) /2 ; e j — орты декартовой системы координат), получим расчетные формулы, позволяющие вычислить упругие модули c f : c f = ( T _a)/^eo . Если же в (3) задать S ₀ = 0, 9 ₀ * 0, то из такой краевой задачи (1)-(3) можно найти эффективные коэффициенты температурных напряжений: в f =- ( T _a)/ 9 ₀ . Важным обоснованием выбора краевого условия вида (3) является то, что при нем между полями напряжений и деформаций неоднородной среды и среды сравнения имеют место равенства: (S) = (S ₀) , (T ■ S) = (T _o ■ S 0) . Таким образом, при выбранном краевом условии у двух рассматриваемых сред оказываются одинаковыми и их механические потенциальные энергии. Отметим, что доказательство достоверности этого утверждения полностью повторяет доказательство, известное из классической теории упругости [12].

С целью определения эффективных коэффициентов тензора k рассмотрим уравнение теплопроводности (2). Для формулировки соответствующей краевой задачи примем для него следующие граничные условия:

9 = x ■ G ₀ , x еГ ,

где G ₀ — некоторый не зависящий от x постоянный вектор. Очевидно, что 9 = x ■ G ₀ , G = V9 , G = G ₀ , q = q ₀ = - k f ■ G ₀ будут давать решение задачи (2), (4) в объеме Q однородной среды сравнения. Решив задачу (2), (4) для неоднородной среды, предположим, что для нее и среды сравнения равны осредненные векторы потока тепла: (q) = (q ₀^ . В результате найдем уравнение для эффективных модулей композита: k f ■ G q =- (q) , где G ₀ — заданный вектор (см. (4)). Тогда для среды сравнения с анизотропией общего вида несложно вывести формулы, позволяющие вычислить модули теплопроводности k ef . Именно, положив в (4) G ₀ = G₀ e _l , где G ₀ = const, а l = 1, 2, 3 — некоторый фиксированный индекс, получим расчетные формулы для модулей k ef : k ef =-( q ,)/ G ₀ . Обоснованием выбора краевого условия (4) являются равенства (G) = (G ₀) , (q ■ G^ = ^q ₀ ■ G ₀^ , причем последнее соотношение имеет энергетический смысл.

3.    Конечно-элементное решение задач для представительных объемов

С целью решения задач термоупругости (1), (2) с соответствующими граничными условиями для неоднородного двухфазного композитного материала в представительном объеме Q можно перейти к их слабым постановкам и использовать классическую технику конечно-элементных аппроксимаций. Пусть Qh — область, занимаемая конечно-элементной сеткой, Qh cQ, Qh = Uk Qek, где Qek — отдельный конечный элемент с номером к . В случае статических задач на конечно-элементной сетке Qh можно искать приближенное решение {uh « u, 9h «9 } в форме uh (x) = N (x) ■ U,   9h (x) = N (x) ■ T ,

где n : — матрица базисных функций для перемещений; N — вектор-строка базисных функций для поля температуры; U , T — векторы узловых перемещений и температур.

В соответствии с обычной конечно-элементной техникой аппроксимируем континуальную слабую (обобщенную или вариационную) формулировку задачи термоупругости в конечномерных пространствах, связанных с базисными функциями N , N 9 . Для этого подставляем (5) и аналогичные представления проекционных функций в слабую постановку задачи термоупругости для Q _h и приходим к следующей конечно-элементной системе:

K „„ ■ U - K : 9 * T = F , K ее ' T = F •

Здесь F , F _e — векторы, определяемые внешними воздействиями и главными граничными условиями;

K uu = ^ a K k , K _U 0 = ^ a K Uk , K 00 = ^ a K 00 — глобальные конечно-элементные матрицы, составленные из элементных матриц K e^k = B ek * ■ c ■ B ^ek d Q , K ek = B ek * ■ eN ek * d Q , K ek = B t * • k • B ek d Q , UU          U          U                 U 0           U         0                  00          0          0

Q ^ek                                        Q ^ek                                       Q ^ek

B ek = L ( V ) ■ N Uk * , B 0 ^k = V N 0 ^k * в результате ансамблирования ( ^ a ) ; N ek * , N 0 ^k * — соответственно матрица и вектор-строка аппроксимирующих базисных функций, заданных на отдельных конечных элементах.

Отметим, что в задаче определения эффективных упругих модулей и модулей связности (1)-(3) решением уравнений (7) является вектор T = Т ₀ , где Т ₀ — вектор с одинаковыми значениями 0 ₀ во всех узлах. Тогда для вычисления узловых перемещений U из (6) получается система уравнений: K UU ■ U = F u + K _{U 0} ■ T ₀ . Можно также заметить, что задача нахождения модулей теплопроводности (2), (4) оказывается несвязанной, то есть для нее достаточно решать только конечно-элементные уравнения (7).

4.    Моделирование представительных объемов

Для нахождения эффективных модулей термоупругого композита с учетом микроструктуры можно численно (методом конечных элементов) решать соответствующие краевые задачи термоупругости в представительных объемах Q композитных материалов. Рассмотрим композит, первой фазой которого является структурный каркас, а второй фазой — изолированные (закрытые) или связанные друг с другом (открытые) поры. Объем Q выберем в форме куба, который равномерно разбит на меньшее число геометрически одинаковых кубиков — термоупругих восьмиузловых гексаэдральных конечных элементов. Таким образом, в кубической решетке Q имеется L х L х L конечных элементов, где L — целое число. В таком двухфазном композите конечные элементы первой фазы наделим материальными свойствами исходного термоупругого материала; для пор зададим пренебрежимо малые модули жесткости и коэффициенты связности, а коэффициенты теплопроводности положим равными коэффициенту теплопроводности воздуха. Теперь остается только выделить элементы со свойствами пор в соответствии с принимаемой микроструктурой композита.

В случае слабо пористого материала нерегулярной стохастической структуры часть конечных элементов, исходя из задаваемой пористости, случайным образом объявим порами. Отметим, что такая модель легко строится, но она не поддерживает связность элементов первой фазы и не отражает возможной связности элементов второй фазы (закрытые или открытые поры).

С целью создания в кубической решетке связанных структур (кластеров) С.В. Бобровым была разработана иная модель [10]. Согласно этой модели исходный куб составляется из базовых ячеек размером 10 х 10 х 10 кубических конечных элементов. Внутри базовой ячейки строится остов — параллелепипед из конечных элементов, а также создаются цепочки из элементов, соединяющие вершины параллелепипеда (крайние конечные элементы параллелепипеда) с соответствующими вершинами ячейки (крайние конечные элементы базовой ячейки). Линейные размеры параллелепипеда определяются в выбранных пределах датчиком случайных чисел; также случайно генерируются и соединительные цепочки элементов (естественно, что в случаях, когда вершины параллелепипеда совпадают с вершинами ячейки, соединительные цепочки не создаются). Остовный параллелепипед занимает 10% от общего объема ячейки. Таким образом, максимально возможная пористость, которая может быть достигнута в данной модели, составляет 90%.

На рисунке 1 демонстрируются два варианта возможных базовых ячеек: в одной из них остовный параллелепипед имеет размеры 4 х 5 х 5 (слева), а в другой — 4 х 6 х 7 (справа). Представительные объемы

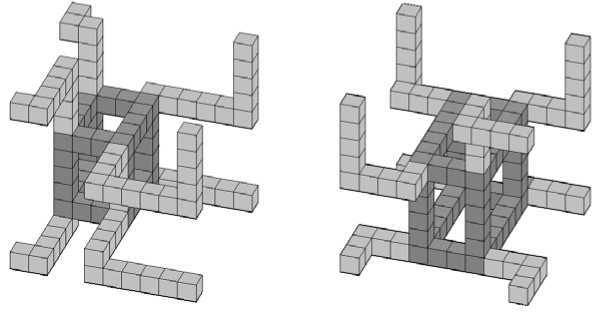
Рис. 1 . Два варианта базовых ячеек размером 10 х 10 х 10 элементов (остовы показаны более темным цветом)

с большим, чем сто, количеством элементов получаются повторением по трем осям координат процедур создания базовых ячеек размером 10 х 10 х 10 элементов. При этом для каждой ячейки случайным образом генерируются размеры остовного параллелепипеда и соединительных цепочек.

Меньшая пористость (вплоть до нуля) достигается в результате применения следующего алгоритма. В построенном на предыдущем шаге представительном объеме случайным образом выбираются два элемента, и если хотя бы один из них не является порой, то эти элементы связываются друг с другом некоторой произвольной цепочкой. Полученное множество добавляется к ранее построенному из твердотельных (термоупругих) конечных элементов каркасу. После этого уточняется пористость, и если она оказывается меньше заданной, то описанный выше шаг алгоритма повторяется: в объеме случайным образом выбираются два элемента и так далее.

На рисунке 2 приведены примеры каркасов, построенных для представительных объемов размером 20 х 20 х 20 при пористости 20% (слева) и при пористости 80% (справа). Для этих объемов базовые ячейки размером 10 х 10 х 10 конструировались различным образом по 8 раз (203/10 3 = 8).

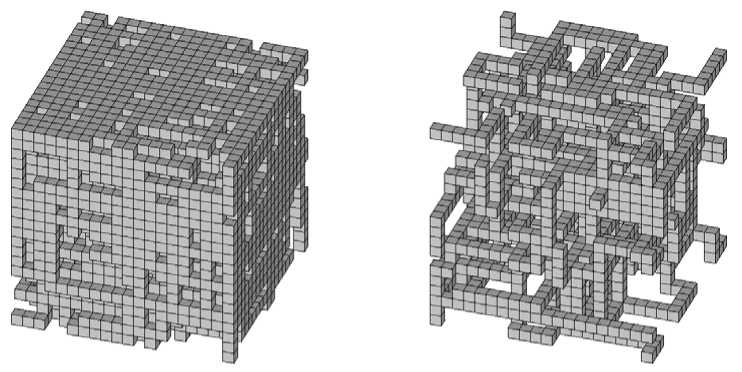
Рис. 2 . Каркасы представительных объемов размером 20 х 20 х 20 элементов, обеспечивающие различную пористость

Итак, описанный алгоритм создания представительных объемов приводит к генерации композитных структур вида пористых кубических решеток и поддерживает связанность структурной матрицы вплоть до пористости в 90%. При этом возможно построение кубических решеток размером 10 m х 10 m х 10 m , где m — целое число. Поскольку на ряде этапов используется датчик случайных чисел, то повторение работы алгоритма при одной и той же заданной пористости каждый раз дает, вообще говоря, новый представительный объем.

Кластерные структуры в кубической решетке можно получать и с помощью алгоритмов теории перколяции. При малой пористости логично строить кластеры из пор, а при большой пористости — кластеры из материала структурного каркаса. Ряд таких методов программно реализован и проанализирован в [11] применительно к пористым пьезоэлектрическим материалам. Но эти методы могут применяться и для представительных объемов пористых термоупругих композитов. Так, метод ограниченной диффузией агрегации или метод Виттена–Сандера [13] позволяет строить кластеры фрактального типа. В стандартном варианте этого метода внутри исходной кубической решетки, состоящей полностью из материала первой фазы, выбирается произвольная частица (элементарный кубик) — зародыш будущей второй фазы. Затем вдали от зародыша задается новая частица, которая блуждает по решетке случайным образом, отражаясь от ее границ. Когда частица подходит вплотную к частицам новой фазы, она прилипает к ним, и, таким образом, ее движение прекращается. После этого берется новая частица первой фазы, и шаг алгоритма с блужданием частицы повторяется. Процедура выбора частицы и ее блуждания длится до тех пор, пока не будет достигнуто требуемое процентное соотношение между фазами бинарного композита. В результате работы данного алгоритма все частицы второй фазы будут связаны между собой, то есть образуется ровно один кластер частиц второй фазы. При больших размерах решетки созданный кластер имеет развитую ветвистую структуру с признаками фрактальности. Однако связанность частиц первой фазы при этом не гарантируется.

Для композитов с существенной поверхностной неоднородностью может оказаться полезной модификация описанного алгоритма, отличающаяся ростом материала второй фазы из определенной плоскости. Частицы запускаются, например, из верхней части решетки и, отражаясь в процессе своего случайного движения от боковых и верхней граней решетки, оседают на ее нижней поверхности, на растущих кластерах новой фазы. В результате происходит рост «деревьев» из частиц второй фазы на нижней поверхности бинарного композита. В отличие от стандартного метода Виттена–Сандера в методе «роста из плоскости» кластеров может быть несколько, но вопрос о связанности частиц первой фазы остается открытым.

На рисунке 3 приведены варианты построенных из пор кластеров для представительных объемов размером 20 х 20 х 20 элементов при пористости 10%. Кластер слева создан по методу Виттена-Сандера, а кластеры справа — по методу «роста из плоскости». В отличие от рисунков 1, 2, темным цветом показаны поры, а элементы термоупругой матрицы не представлены. Кроме того, поскольку кластеры из пор располагаются здесь по большей части внутри, для удобства восприятия приведены также и ребра представительных объемов.

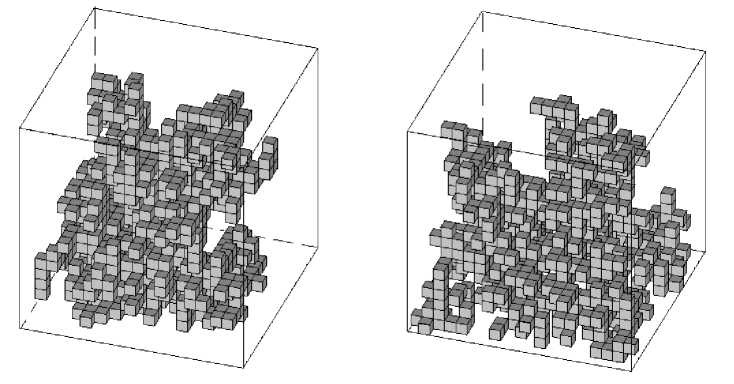
Рис. 3 . Кластеры из пор, построенные по методам Виттена–Сандера (слева) и «роста из плоскости» (справа)

В [11] представлены и другие перколяционные алгоритмы, такие как метод начальной концентрации, методы продольного и поперечного расположения волокон. Все эти методы позволяют строить модели представительных объемов бинарных композитов различной микроструктуры, и в частности, модели пористых анизотропных термоупругих композитов.

5.    Компьютерная реализация и численные результаты

Описанные в предыдущем разделе кубические конечно-элементные решетки создавались с помощью разработанных программ на языке C++. Дальнейшие расчеты эффективных модулей проводились по методике разделов 2 и 3 в конечно-элементном пакете ANSYS 11.0. Для этого построенные конечно-элементные модели представительных объемов передавались в ANSYS вместе с массивами признаков материальных свойств конечных элементов (признак 1 означал структурную матрицу; признак 2 — пору). При решении краевых задач термоупругости (1)–(3) использовались элементы SOLID226 с опциями термоупругого анализа, а при решении задач теплопроводности (2), (4) — конечные элементы SOLID90, предназначенные для теплового анализа. Данные элементы являются гексаэдрами с 20-ю узлами и в совокупности обеспечивают квадратичные по каноническим переменным аппроксимации полей перемещений и температуры.

В качестве примера рассмотрим материал пористого кремния. Как известно [14], кремний является анизотропным материалом кубической сингонии, и, следовательно, структура его материальных констант имеет вид:

" c 11 c 12 c 12 0 0

c 12 c 11 c 12 0 0

c 12 c 12 c 11 0 0

0 0 0 c 44 0

0 0 0 0 c 44

0 " 0 0 0 0

; в = <

в в в 0 0

■; k =

k 0 [ 0

0 k 0

0 1 0 k _

.                           (8)

_ 0

0

0

0

0

c 44 _

к

При расчетах принимались следующие значения материальных модулей кремния с нулевой пористостью (при температуре T = 300 К) [14]: c 11 = c ₂₂ = c ₃₃ = 16,56 - 10¹⁰ Н/м²; c ₁₂ = c ₁₃ = c ₂₃ = 6,39 - 10¹⁰ Н/м²; c ₂₁ = c ₁₂ ;

c 31 = c ₁₃ ; c 32 = c 23 ; c 44 = c 55 = c 66 = 7,95 - 10¹⁰ Н/м²; a = 2,62 - 10 ^{- 6} К^-1; P = a ( c 11 + 2 c ₁₂ ); k = 156 Вт/(м^К). При этом для пор материальные константы (отмеченные знаком «тильда») выбирались равными следующим величинам: c j = к c j ; a = ка ; к = 1 - 10 ^{- 10}; k = 0,025 Вт/(м^К). Как видно из (8), в стационарных задачах рассматриваемый термоупругий материал характеризуется пятью материальными коэффициентами: упругими жесткостями c 11 , c ₁₂ , c 44 ; модулем температурных напряжений P и модулем теплопроводности k .

Будем считать, что модели представительных объемов не имеют ярко выраженной геометрической анизотропии, и поэтому пористый кремний также принадлежит к классу анизотропных материалов кубической сингонии. Тогда для нахождения полного набора его эффективных модулей жесткости и температурных напряжений достаточно решить три задачи (1)–(3) с различными граничными условиями:

I. S0 = 60h1’   00 =0 ^ cj = (T))/^ =Уj^0   (j = 1,2,3),

• II.    S0 =80h4,   60 = 0 ^ c4^ = (TJ/е0 = ^23^/У,

• III.    S0 = 0,   00 *0 ^ P f = T^/Б0 = ^п)/Б0,(11)

причем в (9) при расчетах должно получаться: c e « c 1 3 ff . Решение четвертой задачи (2), (4) позволит определить эффективный коэффициент теплопроводности k ^eff :

• IV.    G 0 = G 01 e 1 ^ k f =- q ₄^/ G 01 . (12)

Итак, четыре краевые задачи для представительных объемов в совокупности дают возможность вычислить по формулам (9)–(12) пять основных материальных термоупругих констант пористого кремния: c 1 iff , c 1 f , c 44 f , P f и k ^ef . По этим значениям можно установить и другие важные константы: упругие податливости s ^e = ( c^ + c ^e )/а ef , s e = - c e /A iff , A f = ( c e ) 2 + c^ c ^e - 2 ( c f ) 2 , s f = ( c f ) 1 ; модуль Юнга E ^ef = 1/ s 1 iff ; коэффициент Пуассона v ^eff =- s 1 2 ⁴ Д1 ^f = c 1 iff Д c 1 iff + c 1 2^f ) ; объемный модуль K ef = E ^ef J |^3 ( 1 - 2 v eff ) J и коэффициент температурного расширения a ^ef = P eff J ( c 1 f f + 2 c 1 ff ) .

На рисунке 4 представлены некоторые из результатов расчетов относительных значений эффективных модулей r (...) в зависимости от пористости p (в процентах). Значения эффективных модулей отнесены к соответствующим значениям модулей материала при нулевой пористости, например, r ( E ) = E ^ef ( p )/ E . Аналогично определены относительные значения объемного модуля K , модуля сдвига G = c 44 и коэффициента теплопроводности k . Всюду на рисунке 4 кривые разного типа соответствуют результатам, полученным при различных способах генерации представительного объема: Con — методом, поддерживающим связность структурного каркаса вплоть до 90%-ной пористости; SR — простым случайным методом; WS — методом Виттена–Сандера; GR — методом «роста из плоскости». Кроме того, на рисунке 4 штриховыми линиями HS показаны кривые для изотропных пористых композитов, вычисленные по приближенным формулам Хашина-Штрикмана [6]: c = p /100; к = 3 ( 1 - 2 v)/2/ ( 1 + v ) , r ( E „s ) = r ( K „ _s ) r ( G_HS ) ( 3 + к )/[ 3 r ( K_HS ) + к r ( G_HS ) ] ; r ( K_HS ) = 1 - ( 3 + 4 к ) c /( 3 c + 4 к ) ; r ( G HS ) = 1 - ( 15 + 20 к ) cl [ 9 + 8 к + ( 6 + 12 к ) c J ; r ( k_HS ) = ( 1 - c )/( 1 + c /2 ) .

Предваряя анализ кривых на рисунке 4, сделаем некоторые замечания. Все расчеты были выполнены с использованием кубических решеток 20 х 20 х 20, описанных в предыдущем разделе. Для простого случайного метода осуществлены последовательно три серии расчетов и после этого вычислены средние значения. Хотя теоретически этот метод может приводить к любым структурам представительных объемов в рамках рассматриваемых кубических решеток, полученные в вычислительных экспериментах композиты не имели признаков структур, генерированных тремя другими методами из раздела 4. Наконец, поскольку при простом случайном методе, методе Виттена–Сандера и методе «рост из плоскости» связность каркаса не поддерживалась, то при большой пористости эти методы давали заниженные значения эффективных модулей, убывающих с ростом пористости.

Результаты, представленные на рисунке 4, показывают, что почти во всех рассмотренных случаях методы Виттена–Сандера и «рост из плоскости» дают близкие значения эффективных модулей. При не слишком большой пористости значения эффективных модулей Юнга и коэффициентов

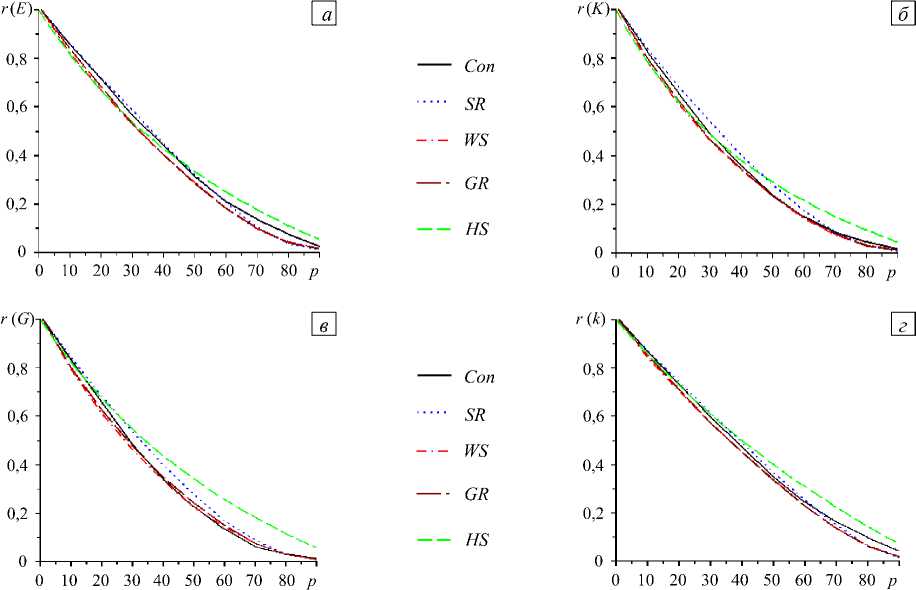
Рис. 4. Зависимости относительных значений эффективных модулей от пористости: r (E) (а), r(K) (б), r (G) (в), r (к) (г) теплопроводности, полученные по методу, поддерживающему связность структурного каркаса, и по простому случайному методу достаточно близки между собой и существенно отличаются от значений, найденных методами Виттена–Сандера и «рост из плоскости». Между тем, значения эффективных модулей (объемного и сдвигового), установленные по методу, поддерживающему связность структурного каркаса, ближе к значениям по методам Виттена–Сандера и «рост из плоскости», чем к значениям, полученным по простому случайному методу. Значения, вычисленные по аналитическим формулам Хашина–Штрикмана для изотропных пористых композитов, при малой пористости достаточно близки к значениям, определенным с помощью методов  Виттена–Сандера и «рост из плоскости», но даже при средней пористости существенно отличаются от значений эффективных модулей, рассчитанных с использованием конечно-элементных программ для всех рассмотренных видов представительных объемов. При большой пористости среди всех исследуемых методов построения представительных объемов можно рекомендовать лишь метод, поддерживающий связность структурного  каркаса, поскольку остальные могут приводить к разрозненным частям матрицы материала и в итоге давать результаты, соответствующие моделям со значительно большей пористостью.

Интерес представляет сравнение полученных данных с численными результатами из [15], где рассматривался пористый кремниевый композит с закрытой пористостью. Там же имеются ссылки на экспериментальные результаты определения механических свойств тонких слоев пористого кремния с открытой пористостью. В [15] решались задачи теории упругости методом конечных элементов в неоднородном представительном объеме со случайным расположением пор при граничных условиях (3) и граничных условиях второго рода с постоянными давлениями. После обработки данных вычислительных экспериментов для задачи с граничными условиями (3) было установлено, что в диапазоне пористости от 0 до 40% с большой долей точности изменение модуля Юнга 1,58504                                                                                 1,77023

аппроксимируется зависимостью r ( E ) « ( 1 - c )     , а изменение модуля сдвига — r ( G ) « ( 1 - c )     .

Среди рассмотренных выше моделей модель, поддерживающая связность каркаса, дает наиболее близкие к степенной зависимости [15] результаты для модуля Юнга, причем во всем диапазоне изменения пористости. К следующим по близости результатам приводит простой случайный метод, что естественно, поскольку аналогичная модель генерации пор использовалась и в [15]. Для модуля сдвига простым случайным методом получаются наиболее близкие с соответствующей степенной зависимостью из [15] результаты, а метод, поддерживающий связанность каркаса, находится по близости к степенной зависимости на втором месте. При этом для пористости более 40% формула 1,77023

r ( G ) « ( 1 - c )      существенно завышает результаты.

6.    Заключение

Итак, в настоящей работе для определения полного набора эффективных модулей термоупругих анизотропных пористых композитов описаны компьютерные конечно-элементные модели представительных объемов различного типа связности, в том числе для высокопористых материалов, сохраняющие связность каркаса вплоть до 90%-ной пористости. Сформулированные задачи механики композитов для термоупругих сред решались численно с использованием специально разработанных программ в конечно-элементном пакете ANSYS.

По результатам расчетов примера для модельного материала, а именно пористого кремния, проанализировано влияние различных структур представительных объемов на значения эффективных модулей. Проведено сравнение величин вычисленных основных характеристик термоупругого пористого материала с рядом известных аналитических и численных данных. Для исследования высокопористых материалов предложен метод, поддерживающий связанность каркаса и дающий адекватные результаты вплоть до пористости в 90%. Результаты тестовых расчетов продемонстрировали, что эффективные материальные свойства пористых термоупругих композитов могут существенно зависеть от моделей представительных объемов.

Работа выполнена при финансовой поддержке Программы развития Южного федерального университета и РФФИ (проекты № 12-01-31411-мол_а, 13-01-00943-a).